1. 引言
从2019年12月开始,武汉市出现了未知肺炎的病例,2020年1月7日,一种新的冠状病毒发现了,该病毒以飞沫和接触为主,传播速度极快。春运很快到来,新型冠状病毒肺炎(简称“新冠肺炎”)迅速蔓延到全国,多地受新冠病毒影响。自疫情暴发以来,人们对新型冠状病毒的了解逐渐深入,国家对疫情应付手段的调整也随之而变,并且对疫情的信息掌控越来越丰富。在此过程中,学者们对疫情开展了预测研究,付新苗 [1] 等人基于2020年1月21日至2月14日的全国及其各省累计病例用Boltzmann函数拟合并且估计临界日期(R2接近0.999)。耿辉 [2] 等人基于SEIR模型分析了相关的措施在防控疫情中起到的作用,此外我们的SEIR模型将基于耿辉等人的模型对参数进行了改进。金启轩 [3] 基于1月23日至2月12日的全国30个省份(不包括湖北省以及港澳台地区)的数据对中国新冠肺炎疫情进行预测建模,我们接下来将使用更新后的数据使用该方法进行建模。
由于前期疫情的诊断治疗流程很繁琐、时间很长,人手,设备和场地也不足,导致每天只能对一定数量的患者进行诊断,因此,湖北省确诊人数的资料反映了目前检测水平,而非实际情况。目前这种情况实际上是医疗能力和诊断标准的问题,本文以相关预测估计中的不足为基础,选择了全国30个省(不包括湖北省和港澳台)的资料,综合了国家防控疫情的措施,并对疫情研究的进展作了建模分析,预测了符合目前实际疫情的发展状况,从而预测了疫情发展的进程,对疫情控制有一定的参考价值。
2. 疫情发展现状及特点
疫情数据来源于国家卫健委及其各个省市卫健委。

Figure 1. National epidemic map on March 13
图1. 3月13日全国疫情图
以2020年3月13日的数据为例,图1为3月13日全国疫情图,从该图我们可以看出每个省市的当日的累计确诊病例,也可以看出各个省市的情况。我们看到与湖北临近的河南、安徽、浙江、湖南、广东等地确诊患病人数非常多,它们的颜色更接近于红色。由黄到红体现了地区患病人数的多少,我们可以清楚的看到这一点。
同样我们可以看到以3月27日数据为基准的,全球疫情图。由图2所示:

Figure 2. Global epidemic map on March 27
图2. 3月27日全球疫情图
我们从1月20号到3月7号选择了每日确诊的人数,以及湖北省的累计确诊人数。从图3中可以看出,从1月20号到2月16号左右,新型肺炎的每日确诊病例,虽然略有上升,但总体表现出上升趋势,而累计确诊病例上升趋势为肉眼可见。可观察到1月27日至之后的一段时期,每天新增的确诊病例有明显的增加,这与病毒检查试剂箱的充分供应有关。2月17日之后,新增病例仍有波动,但我们能看到整体呈下降趋势,而且累积确诊病例上升趋势也逐渐平缓,我们可以认为这种情况已经达到了增速的拐点。由图3可以看出,3月7日后每天新增的确诊病例数已经达到个位,累计确诊人数也逐渐平缓。
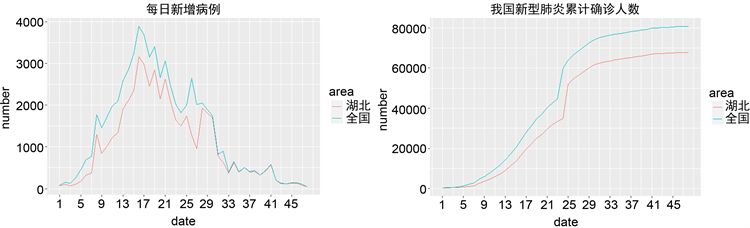
Figure 3. Line chart of daily new cases and cumulative number of confirmed cases in China and Hubei
图3. 全国与湖北地区每日新增病例和累计确诊人数折线图
3. 模型
3.1. 关于全国30个省的相关数据进行建模
我们从1月20日至2月30日分别搜集了全国和湖北省及武汉市的每日新增确诊病例和累计确诊病例,数据来自国家卫健委 [4]、湖北省卫健委 [5] 以及武汉市卫健委 [6]。
全国30省份疫情的性质
对数据观察发现,1月23日前,湖北省之外的其余省份疫情是可控制的。且像武汉市一样的“人传人”现象大都局限在有接触的人之间。之后,国家采取措施,让湖北省内的各市先后禁止开展大型聚集活动且尽量不出门,这极大的限制了病毒的传播。出于一般性考虑,我们只对全国30个省份(除湖北省),因为相对来说,30个省份的数据可靠、及时,只有人传人,初始基数是确定的。我们用1月23日之后的增长率进行了统计和建模。此时增长率=每日新增确诊病例/前一天累计确诊病例,我们记1月25日为第一天,对1月25日至2月20日的增长率进行建模。
由散点图我们可以看到它们是非线性的,根据散点图我们可以尝试用三次函数对其进行拟合。此时模型拟合优度R2为0.959,高度拟合,说明用三次函数来拟合是合适的。此时模型为:
。
3.2. Logistic增长函数
病毒在传播初期,由于政府和民众重视程度不够,传染数据呈指数增长,增长不受抑制。在疫情呈现之后,全国各地隔离了确诊和疑似病例,这一措施阻止了部分病毒的传播,因此传染的速度会逐步遭到压制。我们觉得logistic增长模型 [7] 可用于疫情传播前中期的趋势,因此,我们只选取了1月20日至2月9日的全国累计确诊病例对其进行建模。logistic增长函数的一般形式为:
其中,K为环境容量,
为初始容量,r为增长速率。
此时,我们将1月20日至2月9日的数据进行拟合,可以得到拟合的模型为:
由拟合的模型我们可以看到确诊人数将会在5万左右收敛,而且实际情况远远不止,此时我们要考虑这个模型是否合适。从图4我们看到拟合效果是不错的,残差分布接近均匀,模型拟合的结果还是可以的,并且我们对2月10日至2月15日的累计确诊病例人数进行了预测,预测结果为:43,555.64,44,897.10,45,955.40,46,779.91,47,416.02,47,903.07,我们可以看到对于10日至12日的预测与实际的是非常接近的,但是13日至15日的预测就不那么好了,远小于实际的。因此我们认为此模型对于这些数据来说是不合适的,我们需要考虑到实际的情况,对模型进行修正。

Figure 4. Logistic growth function fitting diagram
图4. Logistic增长函数拟合图
3.3. SEIR模型
此处尝试用SEIR模型揭示2019-nCov的传播过程,模型涉及4类人群:易感人群(S)、潜伏人群(E)、感染人群(I)、移除人群(R),假设康复概率是
,易感染者的感染概率是
,感染者接触的人数是r,潜伏者会传染易感者的概率为
,潜伏者每天接触的人数是
,另假定易感者的感染概率与潜伏者的传染概率相同,则微分方程组如下:
我们根据耿辉 [2] 等人的研究,对模型的参数进行了一些修正,此时我们令
,这个时候我们可以将模型看作是在未干预情况下的爆发趋势。
武汉市卫健委在12月12日对第一例患者发病时间进行了调查,各个领域专家进行了研究探讨,推断该患者的感染时间大致发生在本月初甚至更早,因此,根据SEIR模型,如图5,我们可以预测到在未干预的情况下疫情在二月下旬出现高峰。并且我们用在未干预情况下的预测确诊病例与实际的相比,我们可以看到实际的确诊病例数比预测的值要小得多,特别是越到后面相差越大,出现这种情况是因为国家出台的相关政策起到了作用。

Figure 6. SEIR model fitting diagram with government intervention
图6. 有政府干预时的SEIR模型拟合图
接下来,我们可以考虑在政府进行干预情况下的模型,如图6。此时,有关的参数我们也要进行修正,并且在政府进行强制干预后,感染曲线的减缓趋势明显变得平缓,感染人群的峰值降低了大约1/3、潜伏人群的峰值下降了大约1/2,我们还发现在时间上两者的峰值数据大致相差了七天,从中我们也今天观察到政府的干预以及治疗经验和手段的不断丰富,疫情得到了很大的控制。
4. 结论
由上述拟合我们可以看到,对于增长率而言,1月23日之后,日增长率以三次形式作为模型可高度拟合,并且增长率逐渐趋于零。此时模型为:
。且可以知道,增长率将在3月上旬为0,这与我们的实际情况还是有一些偏差。这是因为国家和整个社会对于病毒的防控起到了作用,当增长率趋于0时,确诊人数就会达到高峰值,之后逐渐减少,最后趋于平稳。我们从logistic增长函数仍可以看出这种趋势,当确诊人数达到一定峰值之后,就会逐渐下降,最后趋于平稳。由拟合的结果我们可以看到确诊人数将会在5万左右收敛,而且实际情况远远不止,累计确诊人数峰值远远高于5万,因此我们认为此模型对于这些数据来说是不合适的,我们需要考虑到实际的情况,对模型进行修正。对于国家的防控疫情措施,我们从SEIR模型可以清楚地观察到,感染人群和潜伏人群的峰值都降低了,这说明政府的强制干预措施对防控疫情起到了很大的作用。
NOTES
*通讯作者。