1. 引言
二维格
中的一个格点
称为是可见的,若没有其它格点位于
与
之间的直线段(不含端点)上。1883年,Sylvester [1] 证明了
中可见格点的比例为
,其中
,
,是黎曼Zeta函数。2018年,Goins,Harris,Kubik和Mbirika [2] 将Sylvester的结果推广到了沿曲线可见的情形。格点
称为是k-可见的,若
位于形如
的曲线上,且在
与
的之间曲线段(不含端点)上没有其它格点。Goins等人证明了
中k-可见格点的比例为
,其他相关研究可参见文献 [3] 和 [4] 等。
最近,刘奎和孟宪昌 [5] 提出了多重k-可见性的概念。对于
,若格点
在形如
的曲线上,且在点
与
之间的曲线段(不含端点)上至多有
个格点,则称点
是l-重k-可见的(见图1)。特别地,当
时,简称
为k-可见格点;当
时,简称
是l-重可见格点。刘奎和孟宪昌给出了方形区域
中1-重和2-重k-可见格点个数的渐近公式。从他们的结果可以得到
中2-重可见格点的密度为
。
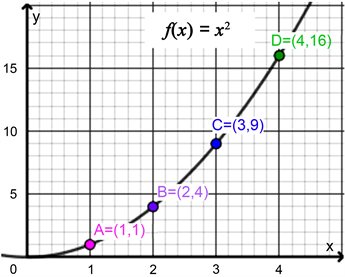 格点A:1-重2-可见;格点A,B:2-重2-可见;格点A,B,C:3-重2-可见;格点D:非3-重2-可见。
格点A:1-重2-可见;格点A,B:2-重2-可见;格点A,B,C:3-重2-可见;格点D:非3-重2-可见。
Figure 1. Higher level 2-visible lattice points along a curve
图1. 沿曲线的多重2-可见格点
本文主要考虑更高重数的k-可见格点。对于
,定义
为
中l-重k-可见格点的集合。
定理1.1. 对于任意的
和给定的
,则
.
注:由于格点的可见性在四个象限里是对称分布的,因此由定理1.1可知,格
中l-重k-可见格点的密度为
。由此及黎曼Zeta函数的定义可知,当l趋于无穷时,该密度趋于1,符合直观。特别地,当
时,定理1.1分别覆盖了上述Goins等人 [2] 以及刘奎和孟宪昌 [5] 的相应结果。
我们还对l-重k-可见格点的密度进行了数值实验(见表1),实验结果与理论结果十分吻合。

Table 1. The density of l-level k-visible points
表1. l-重k-可见格点的密度
根据定理1.1,容易得到以下推论。
推论. 对于给定的
,格
中l-重可见格点的密度为
。
符号说明:
以下是对本文用到的符号的说明。
2. 准备知识
以下广义最大公约数的定义是由Goins等人在 [2] 中提出的。
定义2.1.对
,与参数k有关的广义最大公约数定义为
.
在证明l-重k-可见格点的判别法则之前,我们先证明以下引理。
引理2.1. 对任意
,
,我们有
且
当且仅当
。
证明:若
且
。设
,
。根据
的定义,我们知道d是使得
且
的最大正整数,显然有
。否则,若
,则由
,
,我们有
。同样,由
,
,我们有
。而显然
,这与
矛盾。
反之。若
,设
,则有
。令
,由
的定义,有
,
,从而有
,
。
以下l-重k-可见格点的判别法则是证明定理1.1的关键。
引理2.2. 对
,任意整数
。格点
位于曲线
上,则在点
与点
之间的曲线段上恰好有
个整数格点当且仅当
。
证明:假设
。当
时,点
与点
之间的曲线段(不含端点)上恰好有0个整数格点,即格点
关于原点k-可见,当且仅当
。详细证明细节见( [2],命题3)。
当
时。位于曲线
的连接点
与点
的曲线段(不含端点)上任意整数格点
可以用以下参数形式表示出来:
,
,
。t的所有可能取值的个数即为点
与点
之间的曲线段(不含端点)上的整数格点数。
设
,
。
,则必有
,
,因而有
,
。由引理1.1可知,
,即
。则
为t的全部可能取值。由此得证。
我们还需要用到以下两个熟知的公式。
引理2.3. ( [6],定理2.1)设
是莫比乌斯函数,则对任意整数
,有
引理2.4. ( [6],定理3.2)对
,有
,
其中
是欧拉常数。
3. 定理1.1的证明
设
。由l-重k-可见格点的定义,并运用引理1.2,区域
中l-重k-可见格点数可表示为
, (1)
其中
,
。运用引理1.3,得
.
交换求和顺序,得到
.
因为同余式
且
的解数为
,同余式
且
的解数为
。因此,我们有
.
余项中对
取绝对值,整理得
.
下面整理一下这3个余项。应用引理1.4,第一个余项可得如下估计
.
当
时,第二个余项与第一个余项估计结果相同;
时,由于
是一个收敛级数,因此
,从而
。
故而有
。
扩大上式中求和的范围,得到
。
由于
,因此
。
又因为
,因此,
,
。将
,
,代入(1)式,定理得证。
基金项目
由国家自然科学基金(项目编号:NSFC12071238)资助。