弱Gorenstein投射、内射和平坦复形

Weak Gorenstein Projective, Injective and Flat Complexes

摘要: 本文将弱Gorenstein投射、内射和平坦模的概念推广到复形范畴。首先给出了弱Gorenstein投射、内射和平坦复形的定义；其次在n-Gorenstein环上讨论了弱Gorenstein投射与内射复形；最后给出了一些弱Gorenstein平坦复形的简单性质。

Abstract: In this article, we extend the notion of weak Gorenstein projective, injective and flat modules to the complex category. Firstly, the definition of weak Gorenstein projective, injective and flat complex is given; and then, the weak Gorenstein projective and injective complex is discussed in n-Goren- stein ring. Finally, the simple properties of weak Gorenstein flat complex are given.

1. 引言

投射模、内射模和平坦模是环模理论中最常用也最基本的三大模类，投射模与内射模具有丰富的对偶性，内射模与平坦模也存在丰富的内在联系。1995年，Enochs在文献 [1] 中给出了Gorenstein投射模与内射模的概念，开始了对其一般理论的研究。1998年，Enochs和Jenda在文献 [2] 中研究了n-Gorenstein环上Gorenstein投射与内射复形，把模理论推广到复形。2011年，Yang和Liu在文献 [2] 的基础上把结论推广到一般环上并讨论了Gorenstein投射、内射和平坦复形。Gao比较系统的研究了弱Gorenstein投射、内射和平坦模，2012年Gao在文献 [3] 中给出了弱Gorenstein投射、内射和平坦模的定义，并用它们刻画了几类著名的环。受上述研究的启发，本文将弱Gorenstein投射、内射和平坦模的概念推广到复形范畴。首先给出了弱Gorenstein投射、内射和平坦复形的定义；其次在一些特殊环上研究其简单性质。

2. 预备知识

除非特别声明，环R是具有单位元的结合环，所以涉及的模均是酉模，ModR表示左R模范畴。

定义1 [2] 我们称复形G是Gorenstein投射的，如果存在一个复形的正合序列 $P=\cdots \stackrel{}{\to }{P}_{-1}\stackrel{u_{-1}}{\to }{P}_0\stackrel{u_0}{\to }{P}_1\stackrel{}{\to }\cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $P_i$ 是投射的；

2) $G=Ker{u}_0$ ；

3) 用任意的投射复形Q， $Ho{m}_{C\left(R\right)}\left(P,Q\right)$ 是正合的。

定义2 [4] 我们称复形G是Gorenstein平坦的，如果存在一个复形的正合序列 $F=\cdots \stackrel{}{\to }{F}_{-1}\stackrel{u_{-1}}{\to }{F}_0\stackrel{u_0}{\to }{F}_1\stackrel{}{\to }\cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $F_i$ 是平坦的；

2) $G=Ker{u}_0$ ；

3) 用任意的内射复形I， $I\otimes F$ 是正合的。

定义3 [3] 我们称左R模M是弱Gorenstein投射模，如果存在一个投射左R模的正合序列 $p=\cdots \to p_1\to p_0\to p^0\to p^1\to \cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $p^i$ 和 $p_i$ 是投射的；

2) $M=Ker\left(p^0\to p^1\right)$。

并且称上述正合列p为左R模的弱完全投射分解。

定义4 [3] 我们称左R模M是弱Gorenstein平坦模，如果存在一个左R模的正合序列 $f=\cdots \to f_1\to f_0\to f^0\to f^1\to \cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $f^i$ 和 $f_i$ 是平坦的；

2) $M=Ker\left(f^0\to f^1\right)$。

并且称上述正合列f为左R模的弱完全平坦分解。

对偶的有Gorenstein内射复形与弱Gorenstein内射模的定义，读者可参阅文献 [2] 与 [3]。

3. 弱Gorenstein投射和内射复形

定义3.1我们称复形G是弱Gorenstein投射的,如果存在一个复形的正合序列 $P=\cdots \stackrel{}{\to }{P}_{-1}\stackrel{u_{-1}}{\to }{P}_0\stackrel{u_0}{\to }{P}_1\stackrel{}{\to }\cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $P_i$ 是投射的；

2) $G=Ker{u}_0$。

并且称正合列P是复形的弱完全投射分解。

定义3.2我们称复形G是弱Gorenstein内射的，如果存在一个复形的正合序列 $I=\cdots \stackrel{}{\to }{I}_{-1}\stackrel{u_{-1}}{\to }{I}_0\stackrel{u_0}{\to }{I}_1\stackrel{}{\to }\cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $I_i$ 是内射的；

2) $G=Ker{u}_0$。

并且称正合列I是复形的弱完全内射分解。

推论3.3所有的Gorenstein投射(内射)复形是弱Gorenstein投射(内射)的。

命题3.4设G是复形，则以下等价：

1) G是弱Gorenstein投射复形；

2) 存在一个复形的正合列 $0\to G\to P_0\to P_1\to \cdots$，其中对任意的 $i\in Z$ , $P_i$ 是投射的；

3) 存在复形的正合序列 $0\to G\to P\to N\to 0$，其中P是投射的，N是弱Gorenstein投射的。

证明：根据定义3.1，(1) $\Rightarrow$ (2)，(1) $\Rightarrow$ (3)显然。

(3) $\Rightarrow$ (2)假设存在复形的正合序列 $0\to G\to P\to N\to 0$，其中P是投射的且N是弱Gorenstein投射的。根据定义3.1，存在一个复形的正合列 $0\to N\to P_0\to P_1\to \cdots$ 且对所有的 $i\in Z$ , $P_i$ 是投射复形。因此存在复形的正合列 $0\to G\to P\to P_0\to P_1\to \cdots$ 其中P和 $P_i$ 是投射的。即(2)成立。

(2) $\Rightarrow$ (1)设G是左R模构成的复形，序列 $\cdots \to P_{-2}\to P_{-1}\to G\to 0$ 是复形G的投射分解且每个 $P_i$ 是投射的。结合条件(2)，则存在一个复形的正合序列 $P=\cdots \to P_{-1}\to P_0\to P_1\to \cdots$ 使得 $G=Ker\left(P_0\to P_1\right)$，因此G是弱Gorenstein投射复形。

命题3.5设 $0\to G\to M\to P\to 0$ 是一个复形的正合列。如果G是弱Gorenstein投射复形且P是投射的，那么M是弱Gorenstein投射的。

证明：因为复形G是弱Gorenstein投射的。由命题3.4 (3)知存在一个复形的正合列 $0\to G\to P^{\prime }\to N\to 0$，其中 $P^{\prime }$ 是投射的且N是弱Gorenstein投射的。考虑如下推出图：

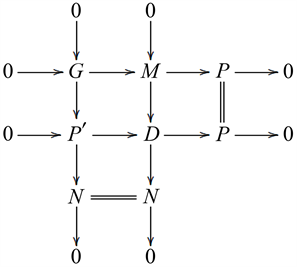
因为中间行序列 $P^{\prime }$ 与P是投射的，所以D也是投射的。又因为中间列序列N是弱Gorenstein投射的，那么根据命题3.4知M是弱Gorenstein投射的。

推论3.6若存在复形的短正合列 $0\to M^{\prime }\to M\to M^{″}\to 0$

1) 如果 $M^{\prime }$ 和 $M^{″}$ 是弱Gorenstein投射复形，那么M是弱Gorenstein投射的。

2) 如果M和 $M^{″}$ 是弱Gorenstein投射复形，那么 $M^{\prime }$ 是弱Gorenstein投射的。

引理3.7我们称环R是Gorenstein环，如果它是双边Noether环且它作为模时有有限的自内射维数。若它的自内射维数为n，则环R是n-Gorenstein环。

定理3.8设R是n-Gorenstein环。如果复形G是弱Gorenstein投射的当且仅当对任意的 $m\in Z$， $G^m$ 是弱Gorenstein投射左R模。

证明： $\Rightarrow$ 设G是弱Gorenstein投射复形，那么存在一个复形的正合序列 $P=\cdots \stackrel{}{\to }{P}_{-1}\stackrel{u_{-1}}{\to }{P}_0\stackrel{u_0}{\to }{P}_1\stackrel{}{\to }\cdots$ 使得对所有的 $i\in Z$， $P_i$ 是投射复形且 $G=Ker{u}_0$。对任意的 $m,i\in Z$，则存在一个ModR上的正合序列 $P^m=\cdots \stackrel{}{\to }{P}_{-1}^m\stackrel{u_{-1}^m}{\to }{P}_0^m\stackrel{u_0^m}{\to }{P}_1^m\stackrel{}{\to }\cdots$，其中 $P_i^m$ 是投射左R模且 $G^m=Ker{u}_0^m$，那么 $G^m$ 是弱Gorenstein投射左R模。

$\Leftarrow$ 由文献命 [3] 题2.6知当环R是n-Gorenstein环时，对任意的 $m\in Z$，弱Gorenstein投射左R模 $G^m$ 是Gorenstein投射的。由文献 [2] 定理4.5，对任意的 $m\in Z$， $G^m$ 是Gorenstein投射左R模当且仅当G是Gorenstein投射的。结合推论3.3可得复形G是弱Gorenstein投射的。

推论3.9如果R是n-Gorenstein环，那么弱Gorenstein投射复形G是Gorenstein投射的。

证明：设R是n-Gorenstein环。若G是弱Gorenstein投射复形，由定理3.8，对任意的 $m\in Z$， $G^m$ 是弱Gorenstein投射左R模。由文献 [3] 命题2.6知弱Gorenstein投射左R模 $G^m$ 是Gorenstein投射的。由文献 [2] 定理4.5， $G^m$ 是Gorenstein投射左R模当且仅当复形G是Gorenstein投射的。故R是n-Gorenstein环时，弱Gorenstein投射复形G是Gorenstein投射的，得证。

注3.10对偶的可以验证命题3.4和3.5以及定理3.8与推论3.6、3.9对弱Gorenstein内射复形也成立。

4. 弱Gorenstein平坦复形

定义4.1我们称复形G是弱Gorenstein平坦的，如果存在一个复形的正合列 $F=\cdots \stackrel{}{\to }{F}_{-1}\stackrel{u_{-1}}{\to }{F}_0\stackrel{u_0}{\to }{F}_1\stackrel{}{\to }\cdots$ 满足以下条件：

1) 对所有的 $i\in Z$ , $F_i$ 是平坦复形；

2) $G=Ker{u}_0$。

并且称正合列F是复形的弱完全平坦分解。

推论4.2所有的Gorenstein平坦复形是弱Gorenstein平坦的。

命题4.3设G是复形，则以下等价：

1) G是弱Gorenstein平坦的；

2) 存在一个复形的正合列 $0\to G\to F_0\to F_1\to \cdots$，其中对任意的 $i\in Z$， $F_i$ 是平坦的；

3) 存在复形的正合序列 $0\to G\to F\to H\to 0$，其中F是平坦的，H是弱Gorenstein平坦的。

证明：证明过程与命题3.4类似。

命题4.4设 $0\to G\to N\to F\to 0$ 是一个复形的正合列。如果G是弱Gorenstein平坦复形且F是平坦的，那么N是弱Gorenstein平坦的。

证明：证明过程与命题3.5类似。

定理4.5若R是一个环且每个内射左R模具有有限的平坦维数，则弱Gorenstein平坦复形G是Gorenstein平坦的。

证明：设G是弱Gorenstein平坦复形，那么对任意的 $m\in Z$，存在ModR上正合序列 $F^m=\cdots \stackrel{}{\to }{F}_{-1}^m\stackrel{u_{-1}^m}{\to }{F}_0^m\stackrel{u_0^m}{\to }{F}_1^m\stackrel{}{\to }\cdots$，使得对所有的 $i\in Z$， $F_i^m$ 是平坦左模且 $G^m=Ker{u}_0^m$，则 $G^m$ 是弱Gorenstein平坦左R模。

不妨设R模E的平坦维数有限，即 $f{d}_R\left(E\right)=n<\infty$。我们对n进行归纳，当 $n=0$ 时， $E\underset{R}{\otimes }{F}^m$ 正合是显然的；当 $f{d}_R\left(E\right)=n$ 且 $1\le n\le \infty$ 时，存在一个正合序列 $0\to M\to F\to E\to 0$，其中F是平坦模且 $f{d}_R\left(M\right)\le n-1$。因此得到复形的正合序列 $0\to M\underset{R}{\otimes }{F}^m\to F\underset{R}{\otimes }{F}^m\to E\underset{R}{\otimes }{F}^m\to 0$，显然 $F\underset{R}{\otimes }{F}^m$ 是正合的，通过归纳 $M\underset{R}{\otimes }{F}^m$ 正合，根据文献 [5] 中定理2.3， $E\underset{R}{\otimes }{F}^m$ 是正合的，从而弱Gorenstein平坦左R模 $G^m$ 是

Gorenstein平坦的。由文献 [4] 定理3.1知对任意的 $m\in Z$， $G^m$ 是Gorenstein平坦左R模当且仅当复形G是Gorenstein平坦的，即证。

推论4.6设R是一个环且每个内射左R模具有有限的平坦维数。如果复形G是弱Gorenstein平坦的，那么 $G^{+}$ 是Gorenstein内射复形。

证明：设复形G是弱Gorenstein平坦的，由定理4.5得弱Gorenstein平坦复形G是Gorenstein平坦的。因此对任意的 $m\in Z$， $G^m$ 是Gorenstein平坦左R模。根据文献 [6] 定理3.6可得 $Ho{m}_Z\left(G^m,Q/Z\right)$ 是Gorenstein内射左R模，由文献 [4] 定理2.8知 $G^{+}$ 是Gorenstein内射复形。

定理4.7若R是右凝聚环，则弱Gorenstein平坦复形构成的类关于直积封闭。

证明：设 $G={\displaystyle \underset{i\in Z}{\prod }{G}_i}$， $G_i$ 是弱Gorenstein平坦左R模构成的复形，下证G是弱Gorenstein平坦复形。因为 $G_i$ 是弱Gorenstein平坦的，所以存在一个复形的正合序列 $F_i=\cdots \to F_{-i1}\to F_{i0}\to F_{i1}\to \cdots$ 使得对任意的 $i\in Z$， $G_i=Ker\left(F_{i0}\to F_{i1}\right)$。因为R是右凝聚环，那么序列 ${\displaystyle \underset{i\in Z}{\prod }{F}_i}=\cdots \to {\displaystyle \underset{i\in Z}{\prod }{F}_{-i1}}\to {\displaystyle \underset{i\in Z}{\prod }{F}_{i0}}\to {\displaystyle \underset{i\in Z}{\prod }{F}_{i1}}\to \cdots$ 是正合的且对任意的 $i,j\in Z$， ${\displaystyle \underset{i\in Z}{\prod }{F}_{ij}}$ 是平坦复形， $G={\displaystyle \underset{i\in Z}{\prod }{G}_i}=Ker\left({\displaystyle \underset{i\in Z}{\prod }{F}_{i0}}\to {\displaystyle \underset{i\in Z}{\prod }{F}_{i1}}\right)$。故G是弱Gorenstein平坦复形，得证。

命题4.8设R是交换环且N是平坦复形。

1) 如果G是弱Gorenstein平坦复形，那么 $G\otimes N$ 是弱Gorenstein平坦的。

2) 如果G是弱Gorenstein内射复形，那么 $G\otimes N$ 是弱Gorenstein内射的。

证明：1)设G是弱Gorenstein平坦复形，那么存在一个复形的正合列 $F=\cdots \to F_{-1}\to F_0\to F_1\to \cdots$，其中对所有 $i\in Z$， $F_i$ 是平坦复形且 $G=Ker\left(F_0\to F_1\right)$。那么 $F\otimes N=\cdots \to F_{-1}\otimes N\to F_0\otimes N\to F_1\otimes N\to \cdots$ 是正合的，其中 $F_i\otimes N$ 是平坦的且 $G\otimes N=Ker\left(F_0\otimes N\to F_1\otimes N\right)$。因此 $G\otimes N$ 是弱Gorenstein平坦的。

2)与1)的证明类似。

参考文献