考虑直流电网关键设备的限流电抗优化配置方法

Optimal Configuration Method of Reactor Considering the Key Equipment in DC Grid

摘要: 直流电网故障快速清除是保证电网持续可靠运行的关键。平波电抗器、故障限流器和混合式断路器等设备可使故障电流发展速度得以削弱，同时，他们对故障电流发展特性也有一定影响，需要进一步研究使平波电抗和故障限流器配置更合理。首先研究了多种限流设备的共同限流下，综合考虑故障限流器的能量吸收及断路器的动作时序，给出了直流电网故障电流计算方法。其次，将减小断路器开断电流和限流设备吸收能量作为优化目标，得到了直流电抗参数配置的优化方法。最后在PSCAD/EMTDC进行仿真验证，结果表明所提优化方法比之前优化方法降低故障开断电流15%。

Abstract: The rapid clearing of DC faults is the key to ensuring the continuous operation of the grid. Equipments such as Current Limited Reactor (CLR), Fault-Current-Limiter (FCL) and hybrid DCCB can weaken the development speed of fault current. At the same time, they also have influence on the development characteristics of fault current. Further research is needed to make the configuration of CLR and FCL more reasonable. Firstly, the current calculation method of DC grid is given considering the energy absorption of FCL and the action sequence of DCCB. Secondly, taking the breaking current of DCCB and the energy absorbed by current limiting equipment as optimization targets, the optimization method of the DC reactance is obtained. Finally, PSCAD/EMTDC simulation verified that the proposed optimization method reduces the fault breaking current by 15% compared with the previous optimization method.

1. 引言

由于电力需求的增加，直流系统互联成网以提供和获取电力。柔性直流电网可控性高，交流侧的有功功率和无功功率快速解耦 [1] [2]，能够接纳多种可再生能源的接入 [3]，是实现多电源供电、多落点受电、能源资源互补优化配置的有效途径，目前国内已建成张北可再生能源柔性直流电网示范工程 [4] [5]。

但是，一旦发生直流故障，故障电流会从互联的各换流站流出，使整个直流电网受到影响。与交流电网相比，直流电网呈现故障电流来源更多、发展速度更快、电网中近端换流站对故障电流的贡献更大以及电网设备耐受过电流能力更弱等特点 [6]。

针对直流电网的故障保护，现有方法主要包含以下三种：

(1) 限制故障后能量源馈入能量 [7]。

(2) 提高故障开断速度 [8]。

(3) 抑制故障电流上升率 [9] [10]。

考虑目前工程应用的DCCB在短时间内开断大容量的故障电流技术上难以实现，因此上述方法(1)和(2)对基于半桥MMC的直流电网来说实现难度较大，故更易于实现的方法是上述的故障限流手段(3)，即增加限流设备如平波电抗器(Current Limited Reactor, CLR)、故障限流器(Fault Current Limiter, FCL)和混合式直流断路器(Hybrid DC Current Breaker, H-DCCB)，并对参数进行优化。

目前对于限流电抗参数优化的论文主要集中在传统高压直流输电的可靠运行及减小经济成本中，如文献 [11] [12] 对于超高压直流输电中的平波电抗进行了优化分析，以防止低负荷时电压断续为约束对电网的平抗进行了优化，文献 [13] 针对一端为海上MMC平台的多端直流系统的电抗器进行了优化配置，考虑了电抗器的质量对海上平台的建设成本的影响。文献 [14] 针对多端直流电网限流电抗配置问题，以限流电抗总感值最小为目标，以故障电流小于DCCB开断电流、MMC不闭锁作为约束进行了优化配置，但其计算过程采用了近似模型，不够精确；文献 [15] 针对平抗的位置进行优化，但是仅考虑了平波电抗器这一种限流设备。文献 [16] [17] 针对多种限流设备的直流电网，在平波电抗器的基础上分析了不同类型故障限流器动作特性，以开断的直流电流最小对平波电抗值进行了优化。但是文献 [17] 使用的故障限流器和DCCB共用一条通流支路，不适用于已建成的断路器拓扑，且两者的动作时序固定，对其他种类的限流器拓扑不具指导意义，没有普适性。以上这些论文没有考虑实际工程中的多种限流设备，没有对多种设备动作过程进行建模分析，优化结果存在一定的不准确，需要进一步地研究。

文章首先分析了故障点两侧FCL和DCCB中的避雷器的能量耗散过程以及断路器动作时序问题，给出了详细的故障电流计算方法。最后，基于得到的故障电流计算方法，得到了适用于直流电网的使故障限流器和断路器吸收能量最小以及开断电流最小的直流侧电抗器的优化配置方法。为含有多种限流设备的直流电网点抗优化配置方法提供了一种思路。

2. 考虑并联MOA的限流电抗器吸能的故障等效建模

典型的电感型FCL主要包括正常运行导通的稳态通流支路和故障后投入的主限流支路 [18]，主限流支路由限流电抗以及并联MOA组成，流经限流电抗和MOA支路的电流分别为i_F，i_MOA，如图1所示，故障限流器的动作原理及时序如图2所示。

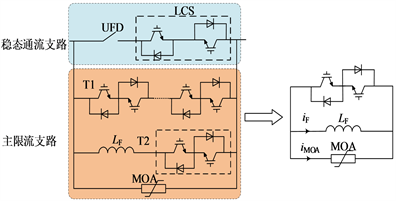
Figure 1. Topology of fault current limiter

图1. 故障限流器拓扑

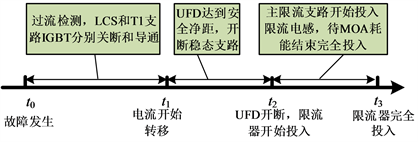
Figure 2. Action sequence and principle of fault current limiter

图2. 故障限流器动作时序及原理

图1中MOA支路的主要元件是金属氧化锌压敏电阻(Metal-Oxide Varistors, MOV)，其V-I特性可以用分段函数特性来表示 [19]。由于限流器主要功能是限流，不具备切断故障电流的能力，因此其额定电压应小于电网电压。

为达到最佳的故障限流效果，故障限流电抗器应该对称安装在换流站出口的正负极线路上。暂不考虑DCCB投入时序的暂态过程对故障电流的影响。在t₂时刻故障限流器中UFD完成开断，开始投入限流电抗和并联MOA时的等效放电回路如图3所示，i_f表示故障电流。

从图中可以看出，限流电抗的增加使得系统时间常数增大，抑制了故障电流上升率。下面具体分析并联MOA支路投退的暂态过程。

当并联MOA及FCL投入瞬间，故障电流流经MOA支路以及限流电抗支路，两条支路电流满足下列关系。

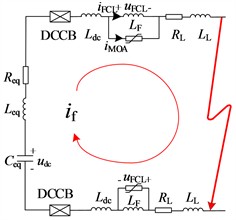
Figure 3. Equivalent circuit after inputting current-limiting reactor L_F

图3. 投入限流电抗L_F后的等效电路

$i_{\text{f}}=i_{\text{MOA}}+i_{\text{F}}$ (1)

在限流电抗刚投入电路时，由于MOA支路与其并联，此时流经MOA的电流即为故障电流i_f，限流电抗上的电流i_F等于0，没有发生电流突变，不会产生过高的电压冲击。根据MOA的V-A特性曲线可知：

$u_{\text{MOA}}\left(i_{\text{MOA}}\right)=L_{\text{F}}\frac{\text{d}\left(i_{\text{f}}-i_{\text{MOA}}\right)}{\text{d}t}$ (2)

当MOA投入电路吸收能量后，在u_MOA降低至比U_MOAn小的时候，MOA退出电路，不再吸收能量，在MOA投退过程中，对文献 [20] 所提的故障电流计算方法的影响是增加了故障两侧限流电抗电流的状态变量，需要增加两个额外的状态方程，如式(8)所示：

$\{\begin{array}{l}A\cdot u=R\cdot i+L\cdot \frac{\text{d}i}{\text{d}t}+{\left[u_{MOA1},u_{\mathrm{MOA}2},0,0,0\right]}^{\text{T}}\\ \frac{\text{d}u}{\text{d}t}=C\cdot i\\ \frac{\text{d}{i}_{\text{F}}}{\text{d}t}=\mathrm{diag}\left(\frac{1}{L_{F1}},\frac{1}{L_{F2}}\right)\cdot {\left[u_{MOA1},u_{\mathrm{MOA}2}\right]}^{\text{T}}\end{array}$ (3)

式中，u_MOA1和u_MOA2分别是故障点两侧限流器的电压，由式(7)决定。i为支路电流矩阵；u为节点电容电压矩阵；A为支路与节点的关联矩阵；R为电阻系数矩阵；L为电感系数矩阵。具体列写方式如文献 [20] 所述，这里不再赘述，矩阵C为：

$C=-diag\left[\begin{array}{cccc}1/C_{\text{C1}}& 1/C_{\text{C}2}& 1/C_{\text{C3}}& 1/C_{\text{C4}}\end{array}\right]\cdot A^{\text{T}}$ (4)

下面解释为什么考虑FCL并联的避雷器支路的能量吸收过程。当FCL无并联MOA时，故障发生到检测到过流后，经过IGBT开关以及UFD开断，故障电流于t₁时刻瞬时转移到限流电抗支路，由于在故障电流转移前和转移后瞬时，限流电抗器遵循磁链守恒定律，即式(5)：

$\left(L_{\text{eq}}+L_{\text{dc}}+L_{\text{L}}\right)\cdot i_{\text{f}}\left(t_{1-}\right)=\left(L_{\text{eq}}+L_{\text{dc}}+L_{\text{L}}+L_{\text{F}}\right)\cdot i_{\text{f}}\left(t_{1+}\right)$ (5)

所以无并联MOA的FCL投入后，故障电流会发生突变，理论上会产生L_Fdi_f/dt = ∞的无穷大电压。这会使得限流器的电压应力极大，需要配置昂贵的防止过压的保护器件，因此实际设计的电抗型FCL都需要并联MOA，此外，从计算的角度来看，当不考虑并联MOA的时候，故障回路将只增加限流电抗而不增加并联支路，故障电流计算将不会增加额外的状态变量，如式(8)所示，最终计算的故障电流峰值将会比考虑并联MOA支路的计算值偏大。故需要在计算故障电流时将MOA支路投退的过程加入加来，使计算结果更加精确且符合工程实际。

3. 考虑混合式断路器动作时序的故障等效建模

故障清除过程的关键设备除FCL之外，最重要的就是高压直流断路器，该设备的动作时序受保护检测时间影响，本文对此不进行深究，但除此之外，断路器自身动作时序也会影响故障电流的发展及开断电流大小。当系统中一点发生故障，故障点两侧的断路器受到跳闸指令后立刻动作，邻近同一换流站的DCCB有相同的动作。由于故障线路两侧的故障电流与故障点位置和故障前初始潮流方向有关，因此故障后两侧断路器即使同时收到动作信号，其动作过程也并不相同，时序上有一定的先后。下面将对这个过程进行分析。

张北工程才用的混合混合直流断路器如图4所示，正常情况下，电流流经主支路，主支路包括超快速隔离开关(Ultra-Fast Disconnector, UFD)和负荷电流开关(Load Current Switch, LCS)。此时主支路等效为阻抗接入支路，阻抗值很小可忽略。t₀时刻线路故障，DCCB在未收到故障指令之前仍保持第一个工作状态。收到跳闸指令后，转移支路的全桥子模块的下桥臂两个IGBT闭合，LCS支路IGBT断开，200 ms后故障电流转移到转移支路，此时断路器仍等效成小阻抗。

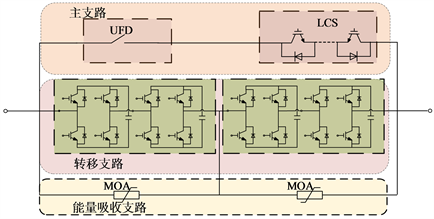
Figure 4. Topology of the cascade full bridge Direct Current Circuit Breaker (DCCB)

图4. 级联全桥直流断路器拓扑

t₁时刻，主支路的机械开关达到安全开距，全桥子模块的下桥臂IGBT断开，故障电流开始向电容充电。此时断路器等效电路为多个子模块电容串联而成的等效小电容。经过约数十ms，在t₂时刻电容电压充到MOA的钳位电压，故障电流转移到能量吸收支路(Energy Absorption Branch, EAB)。能量吸收过程应当位于金属氧化物V-I特性曲线的线性部分，意味着在这个阶段能量吸收支路等效为一个串联的直流电压源。因此t₀-t₁电路等效为小电阻，用标识O表示，t₁-t₂电路等效为电容，用标识C表示，t₂-t₃电路等效为电压源，用标识S表示，t₃时刻以后，直流断路器开断，电路为开路，用标识B表示，动作时序如图5所示。

将故障点两侧直流断路器CB1和CB2的等效电路添加到张北四端故障计算程序中，以MMC1出口侧双极故障为例，改编后的计算过程如下：

(1) CB1和CB2不动作状态(1O2O)

在t₁时刻之前，断路器等效为小电阻，可忽略，故障电流计算方程仍如文献 [20] 所示。

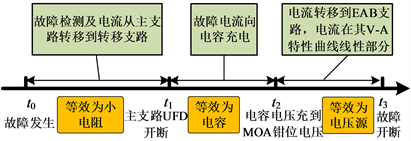
Figure 5. Action sequence diagram of the cascade full bridge DCCB

图5. 级联全桥断路器动作时序图

$\{\begin{array}{l}A\cdot u=R\cdot i+L\cdot \frac{\text{d}i}{\text{d}t}\\ \frac{\text{d}u}{\text{d}t}=C\cdot i\end{array}$ (6)

式中，A、R、L、C矩阵列写方法如文献 [20] 所述，这里不再赘述。

(2) CB1和CB2等效为电容状态(1C2C)

因为CB1和CB2同时收到断路操作的命令，理论上故障点两端的断路器CB1和CB2同时转移到转移支路的电容支路。CB1和CB2等效成串联接入的电容，1O2O阶段最终状态作为1C2C状态的初值。

此时，电路中增加两个电容，使得状态变量增加两个，u_CB1和u_CB2，因此矩阵C需要扩写成式(7)

$C=-diag\left[\begin{array}{llllll}1/C_{\text{C1}}\hfill & 1/C_{\text{CB1}}\hfill & 1/C_{\text{CB}2}\hfill & 1/C_{\text{C}2}\hfill & 1/C_{\text{C3}}\hfill & 1/C_{\text{C4}}\hfill \end{array}\right]\cdot A^{\text{T}}$ (7)

式中，C_CB1表示断路器转移支路子模块电容串联后的等效电容。

(3) CB1等效为直压源，CB2等效为电容阶段(1S2C)

由于CB1和故障点之间阻抗较小，电流上升率更快。因此，CB1领先转移电流到能量耗散支路，此时系统等效电路为1S2C。此时，电路减少了一个电容，增加一个电流源，矩阵C需要扩写成式(8)，KVL方程变为式(9)

$C=-diag\left[\begin{array}{lllll}1/C_{\text{C1}}\hfill & 1/C_{\text{CB}2}\hfill & 1/C_{\text{C}2}\hfill & 1/C_{\text{C3}}\hfill & 1/C_{\text{C4}}\hfill \end{array}\right]\cdot A^{\text{T}}$ (8)

$A\cdot u=R\cdot i+L\cdot \frac{\text{d}i}{\text{d}t}+{\left[\begin{array}{lllll}{u}_{\text{MOA1}}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]}^{\text{T}}$ (9)

(4) CB1和CB2均为直流电压源等效电路(1S2S)

当CB2电流转移到能量吸收支路，CB1和CB2均为等效直流源，此时KVL方程变为式(10)

$A\cdot u=R\cdot i+L\cdot \frac{\text{d}i}{\text{d}t}+{\left[\begin{array}{lllll}{u}_{\text{MOA1}}\hfill & u_{\text{MOA2}}\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]}^{\text{T}}$ (10)

(5) CB1断开CB2直流源状态(1B1S)

此时故障一侧电路已被开断，故障电流状态变量减少一个，KVL矩阵降低一阶。

包括了以上直流断路器各个动作过程的直流故障计算从计算层面来说更加符合实际工程情况，考虑了直流断路器的动作时序的差异，使得电网故障计算更加精确，为后续的电抗器优化配置提供了基础和依据。

4. 考虑MOA的吸能过程和直流断路器动作时序的限流电抗优化

从上述分析可知，直流线路投入的FCL中的电抗值会影响线路的故障限流器和DCCB的能量吸收，进而影响DCCB动作时序以及故障开断电流值。本节将研究出口侧总电抗维持一定的情况下，限流电抗器的优化配置问题。

4.1. 优化目标函数

本节选取的优化目标主要包括两个方面：一个是限流设备的能量吸收，另一个是故障限流器的限流效果。其中限流设备的能量吸收包括电抗型FCL的并联MOA吸收的能量以及混合式DCCB的EAB支路吸收的能量，其能量越小，动作过程越快，越利于故障快速开断；故障限流效果即可以等效为故障后DCCB开断电流值，其值越小效果越好。

MOA中的能量可由式(11)计算得到：

$Q_{\text{MOA}}={\displaystyle {\int }_0^{t_b}{u}_{\text{MOA}}{i}_{\text{MOA}}\text{d}t}$ (11)

式中，Q_MOA为MOA吸收的能量；t_b为MOA投入电路的时间。

从第三节对直流断路器动作的时序分析过程来看，当发生近端故障时，故障点两侧DCCB吸收的能量不同导致了两个断路器动作时序的差异，两者吸收的能量不是简单的相等关系或者仅需计算一端能量，另一端可以忽略的情况。因此能量计算时不仅需要计算近端DCCB中吸收的能量，还需要计算对侧DCCB中吸收的能量，在某些情况下两者的数值几乎是相近的。

根据式(3)~(5)可知，直流侧电抗器的配置影响了直流侧故障电流的大小。又根据式(8)~(10)和式(11)可知，限流电抗器L_F的配置影响了故障限流器和直流断路器中MOA吸收能量的大小。本小节优化目标为使得直流断路器的开断电流和故障限流器和直流断路器中的MOA吸收的能量之和尽可能的小，从而减小直流断路器的开关器件数量以及防止MOA的热超载。故障后FCL经过1.5 ms电流异常检测时间开始动作，2 ms UFD动作延时后3.5 ms开始投入限流电抗及MOA；混合式DCCB经过2 ms的检测时间动作，再经过UFD 2 ms动作延时达到额定开距，转移支路开关切换使得故障电流对电容充电，充到避雷器额定电压时MOA动作，完成故障电流开断。

目标函数可用式(12)表示，约束条件里包含四条线路各个站出口的双极短路故障情况。

$\begin{array}{l}\min F=\min \left({\displaystyle \underset{i=1}{\overset{n=8}{\sum }}{I}_{\text{b}}},{\displaystyle \underset{i=1}{\overset{n=8}{\sum }}{Q}_{\text{MOAS}i}}\right)\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}{I}_{\text{b}}\le 15\text{kA}\\ I_{\text{dcpk}}\le 18\text{kA}\\ I_{\text{b}}<I_{\text{dc}}\left(t=3.5\text{ms}\right)\\ L_{i=1~8}\ge 0.015\text{H}\end{array}\end{array}$ (12)

式中，Q_MOAS为FCL和DCCB共同吸收的能量，各电流含义如上所述。

4.2. 多目标优化

针对上一小节所提的故障电流最小和吸收能量最小的多目标优化问题，可以使用变动权系数法进行处理。分别给优化目标F的两个子目标以不同权重k_i，做线性加权函数，把多目标问题转化为如下问题：

$\begin{array}{l}\{\begin{array}{l}F=k_1{f}_1+k_2{f}_2\\ k_1+k_2=1\end{array}\\ \min F\end{array}$ (13)

利用模拟退火智能算法(Simulated Annealing Algorithm, SAA)对式(13)进行优化求解，从而实现平波电抗器和故障限流器的优化配置。优化流程图如图6。

Figure 6. SAA optimization process of current limiting reactor

图6. 限流电抗器SAA优化流程

图6中k为循环计数变量。T为初始温度，q为冷却比率，d为领域大小，T_end为最终温度，这些都是SAA算法的固有参数，需要在求解开始时输入，将这些参数提供给算法循环。T、q、d和T_end参数决定SAA优化算法的两个迭代环的循环次数，内环循环每次迭代d次，最终收敛结束的判据是外环的温度小于最终温度T_end，此时优化过程结束。L₁和L₂分别是电抗器初始取值和每次内迭代环最初的新值。

目标函数通过罚函数进行修正，选取罚函数因子为M=10⁷。目标函数修正为：

$\begin{array}{l}\min F^{\prime }=\min F+M{\left(\min \left[15-I_{\text{b}},0\right]\right)}^2+\cdots \\ +M{\left(\min \left[18-I_{\text{dcpk}},0\right]\right)}^2+\cdots \\ +M{\left(\min \left[I_{\text{dcpk}}-I_{\text{b}},0\right]\right)}^2+\cdots \end{array}$ (14)

式中，min[a,b]表示为取a和b中较小的值。

5. 仿真验证

使用PSCAD/EMTDC搭建了如图7所示的张北四端真双极带金属回线的仿真模型，其参数如表1所示。在仿真系统，四端换流站主要电路参数相同，每条线路两端配备DCCB以及FCL。DCCB采取级联全桥混合式拓扑，MMC采取半桥拓扑。

Table 1. Four-terminal DC grid MMC parameters

表1. 四端直流电网MMC参数

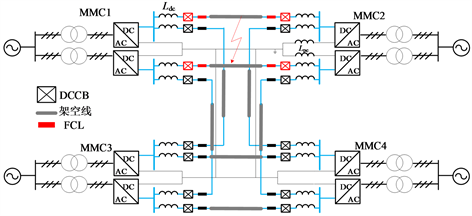
Figure 7. Four-terminal DC grid topology

图7. 四端直流电网拓扑

当直流电网出口侧平波电抗和故障限流器中的电抗之和一定为150 mH时，不同平波电抗和故障限流电抗组合下，如图7所示临近换流站MMC2出口(稳态电流I₁ = −1.8299 kA)和MMC1出口(稳态电流I₁ = 1.8299 kA)故障后电流如图8所示。

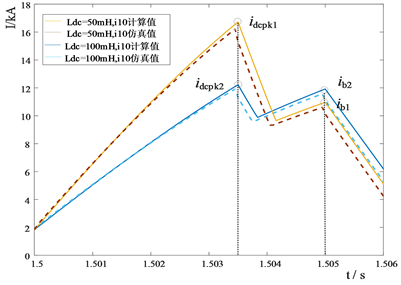(a) MMC1出口故障电流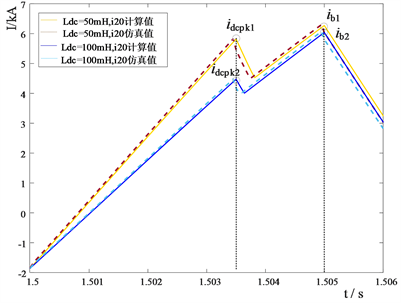(b) MMC2出口故障电流

Figure 8. DC fault current under different DC reactance combinations

图8. 不同直流电抗组合下直流故障电流

首先从图8(a)和图8(b)可以看出，考虑了限流电抗器及断路器动作时序后的故障电流计算与仿真结果之间差异很小，表明了理论分析的正确性。其次，从表2可以看出，线路上的平波电抗和限流器电抗在不同组合的情况下，故障开断电流以及故障限流器和断路器的MOA支路吸收能量均有差异。如在MMC1出口故障，电抗越大，故障电流峰值越小(i_dcpk2 < i_dcpk1)，此时故障限流器中的MOA吸收能量更小，但是5 ms时刻故障开断电流更大(i_b2 > i_b1)，这直接导致了断路器吸收能量增加以及断路器需要的开断能力的提升。

Table 2. Energy Absorption by FCL and DCCB under Different CLRs

表2. 不同平抗下故障限流器和断路器吸收能量

当式(11)中的k₁ = 1，k₂ = 0和k₁ = 0，k₂ = 1时，即分别以各个故障点开断电流之和最小(f_1.min)和各个故障点故障限流器和直流断路器的MOA能量之和最小(f_2.min)为单目标求解，分别求得f_1.min = 72.9799 kA和f_2.min = 254.4105 MJ。与文献 [16] 优化时未考虑直流断路器器动作时序时的优化结果相比较，本文优化计算得到的MOA吸收能量更多，开断的故障电流更小，下降了15.88%，本质上是由于本文所提方法计及了故障线路两侧断路器中的MOA能量，相较于文献 [20] 计算方法更加精确，更加贴近于实际工程。分别采取不同的权重系数，对两个目标函数分别配以不同权重，来进行直流电抗器的优化选取，得到的结果如表3所示。实际应用中，可以根据对断路器开断能力和避雷器吸收能量的重要程度来选取不同的参数组合。

Table 3. Optimization results of DC reactors under different weights

表3. 不同权重下直流电抗器优化结果

6. 结论

本文以张北四端真双极带金属回线直流电网为研究对象，分析了包含多种限流设备如平波电抗器、电抗型FCL和级联全桥DCCB的直流电网的故障特征。得到如下结论：

(1) 对故障限流器中的吸能元件能量吸收过程和故障两侧断路器动作时序进行建模，给出了考虑多种限流设备动作的直流电网故障电流计算方法。

(2) 利用模拟退火算法给出了直流电网各条线路上的限流电抗器优化配置的方法，保证了在经济成本一定的情况下，限流效果达到最优。为直流侧限流电抗器参数的优化配置提供了理论依据。

基金项目

国家重点研发计划资助项目(2018YFB0904600)。