聚焦波与多个潜堤相互作用的数值模拟

Numerical Simulation of Focused Wave Interaction with Multiple Submerged Breakwaters

摘要: 潜堤具有促淤保滩、防波等作用，在港口、航道等工程中应用广泛；极端波浪由于其瞬时出现、波高大、破坏力强，严重影响在航道中航行船舶的安全。为分析极端波浪与潜堤的作用机理，保护航行船舶安全，本文基于非静压模型SWASH (Simulating WAves till SHore)，开展聚焦波与多个潜堤相互作用的数值模拟，研究矩形潜堤高度、宽度、间距和个数对聚焦波特征参数的影响。结果表明：多个潜堤能够有效地抑制极端波浪；随着潜堤高度、宽度、间距和个数的增加，聚焦波峰值下降，聚焦位置以及时间后移；当潜堤间距与潜堤宽度所对应的共振频率相近时，随着潜堤个数的增加，聚焦波能会显著地向倍频附近转移。

Abstract: Submerged breakwaters have the advantages of beach protection and siltation accretion as well as break waves, which are widely used in port and waterway projects. Extreme waves seriously affect the safety of ships sailing in the fairway due to their instantaneous appearance, high wave height and strong destructive power. Therefore, it is necessary and important to analyse the mechanism of the interaction between the extreme waves and submerged breakwaters to protect the safety of sailing ships. This paper carries out a numerical simulation of focusing waves interacting with multiple submerged breakwaters based on a non-static pressure model SWASH (Simulating WAves till SHore). The effects of height, width, spacing and number of rectangular submerged breakwaters on focused wave characteristic parameters were studied. The results show that multiple submerged breakwaters can effectively suppress extreme waves. With the increase of height, width, spacing and number of submerged breakwaters, the peak value of focused wave decreases, and the focused position as well as the focused time moves backward. When the distance between the submerged breakwaters is close to the resonance frequency corresponding to the width of the submerged breakwaters, as the number of submerged breakwaters increases, the focused wave energy will significantly transform to the second order frequency.

1. 引言

在水环境生态保护的大背景下，传统的重力式防波堤因其极大地削弱了海水的自交换能力，产生一系列的环境问题，在港口、航道工程中应用逐渐变少。潜堤作为一种布置在水下的挡浪结构，由于其对环境影响极小，且具有促淤保滩、防波等作用，在港口、航道等工程中应用日益广泛。

极端波浪是一种最大波高超过有效波高2倍以上的灾害性波浪 [1]，由于其波高大、破坏力强，且出现时没有明显的规律，一旦当其出现在航道中，会严重危害航行船只的安全。如何对极端波浪进行防治，是一个亟待研究的问题。为此，本文提出一种利用多排潜堤来抑制极端波浪的方法，主要利用潜堤的浅水作用有效地衰减波浪，并将波浪的基频能量转化为更易耗散的高频能量 [2]，进而保护航道中的船舶航行安全。

目前，相位聚焦是在实验室中产生极端波浪的一种主要手段，但由于聚焦波的复杂性，现有研究大多关于均匀地形条件下或者在单个结构物下，针对聚焦波与多个矩形潜堤相互作用规律尚缺乏相关研究 [1] [2] [3] [4]。基于此，本文采用非静压模型SWASH (Simulating WAves till SHore)利用边界速度造波的方式，开展聚焦波与多个潜堤相互作用的数值模拟研究，探究其作用机理并为相关生产实际提供理论依据。

2. 数值方法

2.1. 基本控制方程

非静压模型SWASH基于非定常不可压缩及雷诺平均条件下的Navier-Stokes方程，忽略风应力以及表面张力，并将动量方程中的压力p写为静水压力p_h以及非静水压力q之和：

$p=p_h+q=g\left(\eta -z\right)+q$ (1)

式中：η为自由面，将上式带入动量方程中可得二维条件下非静压模型的控制方程如下：

$\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0$ (2)

$\frac{\partial u}{\partial t}+\frac{\partial u^2}{\partial x}+\frac{\partial uw}{\partial z}+g\frac{\partial \eta }{\partial x}+\frac{\partial q}{\partial x}={\nu }_H\frac{{\partial }^{2}u}{\partial x^2}\text{+}\frac{\partial }{\partial z}\left({\nu }_V\frac{\partial u}{\partial z}\right)$ (3)

$\frac{\partial w}{\partial t}+\frac{\partial wu}{\partial x}+\frac{\partial w^2}{\partial z}+\frac{\partial q}{\partial z}={\nu }_H\frac{{\partial }^{2}w}{\partial x^2}+\frac{\partial }{\partial z}\left({\nu }_V\frac{\partial w}{\partial z}\right)$ (4)

式中：u、w分别为x、z方向上的速度，t表示时间，g为重力加速度， ${\nu }_H$ 和 ${\nu }_V$ 为水平向以及垂向的涡粘系数。

2.2. 聚焦波理论及边界造波

在二维情况下，多个线性波组成的波面方程可以表示为各个组成波波面方程的线性叠加，即

$\eta \left(x,t\right)={\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_j\cos \left(k_{j}x-{\omega }_{j}t+{\epsilon }_j\right)}$ (5)

式中：N为波列中组成波的个数，a_j、k_j、ω_j、ε_j分别表示第j个组成波的振幅、波数、圆频率以及相位。

聚焦波是一种特殊的不规则波，由于不同周期的波速不同，在某个特定的时间以及特定的位置，会出现所有波的峰值叠加。设在t = T_p (聚焦时间)，所有组成波都在x = F_p (聚焦位置)处聚焦，则波面方程可以表示为下式：

$\eta \left(x,t\right)={\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_j\cos \left[k_j\left(x-F_p\right)-{\omega }_j\left(t-T_p\right)\right]}$ (6)

为实现数值波浪水槽的造波与消波，本文采用速度边界法造波，以及Jacobsen [5] 提出的松弛法来消除透射波避免二次反射。在线性波理论下，造波边界处的自由面η，水平速度u，垂向速度w可以表示为：

$\eta ={\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_j\cos \left[k_j\left(0-F_p\right)-{\omega }_j\left(t-T_p\right)\right]}$ (7)

$u={\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_j{\omega }_j\frac{\cosh \left(k_j\left(z+h\right)\right)}{\sinh \left(k_{j}h\right)}\cos \left[k_j\left(0-F_p\right)-{\omega }_j\left(t-T_p\right)\right]}$ (8)

$w={\displaystyle \underset{j=1}{\overset{N}{\sum }}{a}_j{\omega }_j\frac{\sinh \left(k_j\left(z+h\right)\right)}{\sinh \left(k_{j}h\right)}\sin \left[k_j\left(0-F_p\right)-{\omega }_j\left(t-T_p\right)\right]}$ (9)

式中：h为水深；在造波边界处给定上述条件便可在指定时间、指定位置处生成聚焦波。

3. CFD数值模型验证及模型布置

3.1. CFD数值模拟布置

CFD (Computational Fluid Dynamics)数值波浪水槽布置见图1，水槽长度为60 m，水深h = 0.5 m，水槽首端采用速度边界法造波，水槽末端50~60 m采用松弛法消波，并在60 m处设置辐射边界条件避免二次反射。首个矩形潜堤布置在x = 14 m处，潜堤高度设为H_b，潜堤长度设为W_b，潜堤之间的间距设为L_b，潜堤个数设为n。聚焦波设置为等振幅谱(即不同组成波的输入波高相等)，聚焦波高A_f = 0.06 m，聚焦波频率范围为f_min~f_max (f_min = 0.53 Hz, f_max = 1.13 Hz)，组成波个数N = 29，聚焦时间T_p = 40 s，聚焦位置F_p = 25 m。同时水槽中在24~29 m处设置501根浪高仪用来监测波浪的聚焦时间以及聚焦位置(水槽中出现的最大波峰值对应的时间和位置为实际聚焦时间和聚焦位置)，分别为G1~G501，间隔0.01 m。

为研究矩形潜堤高度、宽度以及潜堤间距和潜堤个数对聚焦波聚焦位置、聚焦时间以及聚焦波能的影响，设置数值模拟工况具体见表1。

Figure 1. Schematic diagram of a numerical wave flume

图1. 数值波浪水槽示意图

Table 1. Conditions of numerical simulation

表1. 数值模拟工况表

3.2. 数值模型验证

为验证数值模拟的可靠性，本文将数值模拟结果与前人试验结果进行对比 [4]。图2表示在聚焦振幅A_f = 0.06 m，水深h = 0.5 m，聚焦波频率f_min = 0.53 Hz，f_max = 1.13 Hz，组成波个数N = 29 (等振幅谱)，聚焦时间T_p = 25 s，聚焦位置F_p = 11.54 m的条件下，CFD结果与试验结果的波面曲线对比。从图中可以看出，不同测点处的试验结果与CFD模拟结果几乎一致。上述结果表明，边界造波法能较好的模拟聚焦波的生成，模型可靠。

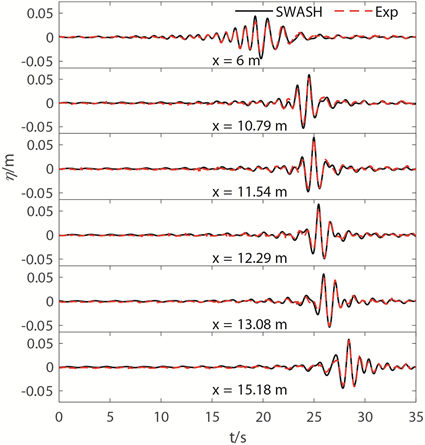
Figure 2. Comparisons of experimental and CFD focused wave surface

图2. 试验及CFD聚焦波面对比

4. 结果与讨论

4.1. 空水槽模拟结果

聚焦波在传播过程中涉及波浪的非线性变化以及波波之间相互作用，设计的聚焦波并不一定在设定参数T_p = 40 s、F_p = 25 m处聚焦。为使波浪在指定处聚焦，需对输入参数进行率定；经过多次率定，得到聚焦点处的聚焦波面以及聚焦频谱如图3所示：

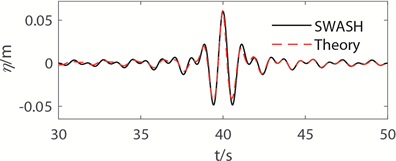(a) 聚焦波自由面 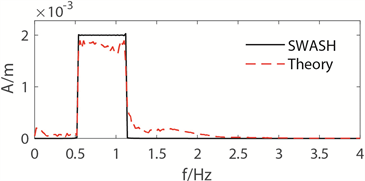(b) 聚焦波频谱

Figure 3. Comprasions of focued wave between CFD simulation and theoretical solution

图3. CFD及理论聚焦点处的聚焦波对比

上图表明，当波浪传播到聚焦位置处时，由于波浪的非线性变化以及波波之间相互作用，虽然部分聚焦波能量向高频部分转移，但SWASH模拟所得聚焦波波形与理论值差异不大，表明本模型的设计参数可用来模拟聚焦波的产生。

4.2. 单潜堤与聚焦波作用

4.2.1. 潜堤高度对聚焦波的影响

图4表示当潜堤个数n = 1，潜堤宽度W_b = 1.5 m时不同潜堤高度H_b对聚焦波的影响，其中图4(a)为聚焦特

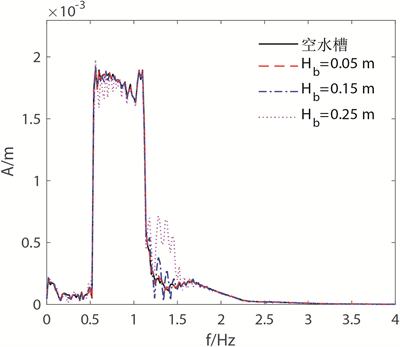(a) 聚焦特征参数 (b) 聚焦点处频谱

Figure 4. Effects of different submerged breakwaters’ height H_b on the focused wave under the conditons of the number ofsubmerged breakwaters n = 1 and the width of submerged breakwaters W_b = 1.5 m

图4. 不同潜堤高度H_b对聚焦波的影响；潜堤个数n = 1，潜堤宽度W_b = 1.5 m

征参数随潜堤高度的变化，图4(b)为聚焦点处频谱的变化。从图4(a)中可看出，随着潜堤高度的增加，聚焦波峰值急剧下降，当潜堤高度为0.35 m时，聚焦峰值相较于空水槽下降了17%，可以预见，当潜堤高度大于水深时，聚焦峰值将为零；此外，聚焦时间以及聚焦位置都随着潜堤高度的增加而呈现出近乎线性的增长。图4(b)则直观解释了上述现象的成因，当波浪经过潜堤时，随着潜堤的高度增加，由于波浪的浅化作用，波浪非线性在不断增强，部分波浪能将从基频转化到倍频，在此过程中，部分波浪能也被潜堤所耗散，由此，聚焦波峰值不断下降。

4.2.2. 潜堤宽度对聚焦波的影响

图5表示当潜堤个数n = 1，潜堤高度H_b = 0.25 m时不同潜堤宽度W_b对聚焦波的影响，其中图5(a)为聚焦特征参数随潜堤宽度的变化，图5(b)为聚焦点处频谱的变化。从图5(a)中可看出，聚焦波峰值随着潜堤宽度的增加先减小，而后呈现出周期性的振荡，聚焦时间以及聚焦位置都随着潜堤宽度的增加而不断增大。观察频谱图可以发现，在潜堤宽度的变化过程中，整体能量变化不大，表明当潜堤高度固定时，潜堤宽度对聚焦波的影响有限。聚焦波峰出现周期性的振荡则是由于波浪在潜堤上发生共振所致，根据线性波浪理论可以计算出本文模拟的波浪波长范围在1.2~3.8 m，模拟结果显示当波长潜堤宽度在1.5 m的整数倍时(注意到此数值约为聚焦波波长区间的中值)聚焦峰值处于最小值，表明当潜堤宽度处于该值的整数倍时，发生共振的各个组成波更多，从而引起聚焦波峰值下降。

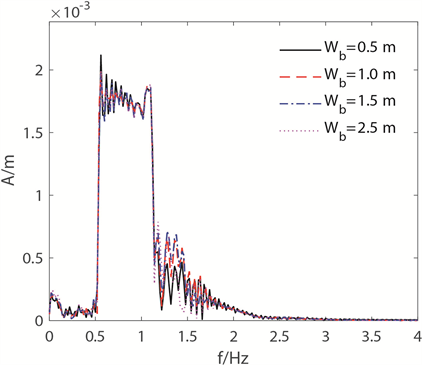(a) 聚焦特征参数 (b) 聚焦点处频谱

Figure 5. Effects of different submerged breakwaters’ width W_b on the focused wave under the conditons of the number of submerged breakwaters n = 1 and the height of submerged breakwaters H_b = 0.25 m

图5. 不同潜堤宽度W_b对聚焦波的影响；潜堤个数n = 1，潜堤高度H_b = 0.25 m

4.3. 多潜堤与聚焦波作用

4.3.1. 潜堤间距对聚焦波的影响

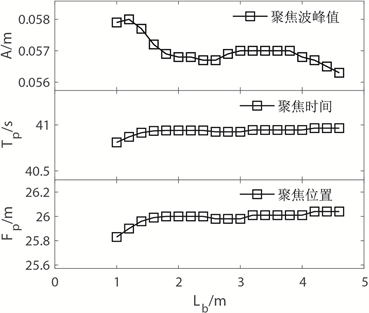
图6表示当潜堤个数n = 2，潜堤高度H_b = 0.25 m，潜堤宽度W_b = 1.0 m时不同潜堤间距L_b对聚焦波的影响，图6(a)、图6(b)分别为聚焦特征参数随潜堤高度的变化曲线以及聚焦点处频谱的变化曲线。从图6(a)中可看出，聚焦波峰值随着潜堤间距的增加先减小而后开始周期性振荡，聚焦时间以及聚焦位置都随着潜堤间距的增加先增加而后几乎不变。观察频谱图可以发现，在潜堤间距的变化过程中，不同间距所对应的二阶共振频率不同。上述现象的主要由于潜堤之间的布拉格共振作用 [6]：当潜堤间距为波浪半波长的整数倍时，对应频率的波浪共振作用最强。观察图5(b)可以发现，单个宽度为1 m的潜堤，其产生的高阶频率在 1.3~1.5附近，同时0.65~0.75 Hz范围内的波浪能量相较于空水槽出现明显的减小。

将图6(b)与图5(b)对比，可以发现，当潜堤间距变化时，高频部分的能量将发生周期性的移动，同时当潜堤间距与潜堤宽度本身引起的共振一致时，高频部分会有明显的增大。如潜堤间距为3.2 m时，该距离约为波长1.6 m、2.1 m、3.2 m的半波长整数倍，对应波浪频率为0.95 Hz和0.82 Hz，0.61 Hz，图中可以看到该频率对应的峰值下降，高频部分在1.22 Hz、1.5 Hz处出现了峰值，剩下的倍频峰值不明显。可以认为1.22 Hz所对对应的波能由布拉格共振产生而1.5 Hz对应的能量则是潜堤本身所引起的。同理潜堤间距为2.4 m时，波长1.6 m、2.4 m的波浪对应波浪频率0.97 Hz、0.75 Hz，在图中可以看到该频率对应的峰值下降，但对应的倍频1.4~1.5 Hz附有明显的峰，该能谱宽度大于潜堤间距为3.2 m时，上述现象表明，表明当布拉格共振与本身潜堤共振频率一致时，布拉格共振能够促进的高频波产生，并扩大高频波的范围。

(a) 聚焦特征参数 (b) 聚焦点处频谱

Figure 6. Effects of different submerged breakwaters’ distance L_b on the focused wave under the conditons of the number of submerged breakwaters n = 2 and the height of submerged breakwaters H_b = 0.25 m as well as the width of submerged breakwaters W_b = 1.5 m

图6. 不同潜堤间距L_b对聚焦波的影响；潜堤个数n = 2，潜堤高度H_b = 0.25 m，潜堤宽度W_b = 1.0 m

4.3.2. 潜堤个数对聚焦波的影响

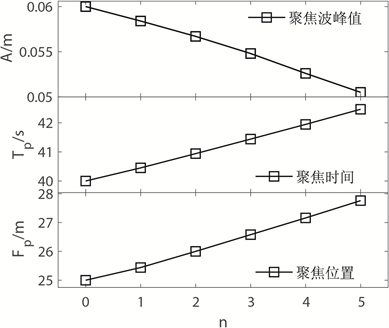
图7表示当潜堤间距L_b = 2.4 m，潜堤高度H_b = 0.25 m，潜堤宽度W_b = 1.0 m时不同潜堤个数n对聚焦波的影响，图7(a)、图7(b)分别为聚焦特征参数随潜堤高度的变化曲线以及聚焦点处频谱的变化曲线。据上文可知，当潜堤宽度为1 m时，单个潜堤的二阶共振频率在1.25~1.5 Hz附近；同时当潜堤间距为2.4 m时，布拉格共振频率也在1.5 Hz附近。当两者协同作用时，可以发现，随着潜堤个数的增加，聚焦波峰值会明显的减小，且该值随着潜堤个数的增加近乎线性减小；聚焦时刻和聚焦位置随着潜堤个数的增加近乎线性增大。此外发现，当单个潜堤的共振倍频和布拉格共振对应的频率相近时，随着潜堤个数的增加，此时高频波随着潜堤个数的增加近乎线性放大，此时两者协同共振所产生的高阶波远远大于基频波浪的幅值，如当潜堤个数为5时，对应的二阶幅值已大于基频值。在实际应用中，聚焦峰值明显的下降意味着波浪破坏力的下降，同时高频波相较于低频波更容易耗散以及被人们消除，故上述研究对实际航道中船舶的航行具有重要意义。

(a) 聚焦特征参数 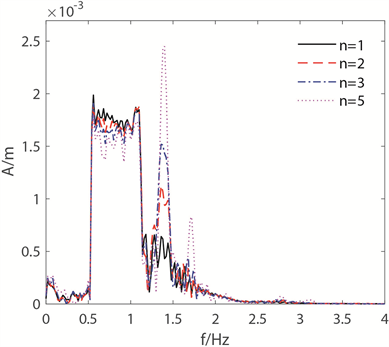(b) 聚焦点处频谱

Figure 7. Effects of different submerged breakwaters’ number n on the focused wave under the conditons of the distance of submerged breakwaters L_b = 2.4 m and the height of submerged breakwaters H_b = 0.25 m as well as the width of submerged breakwaters W_b = 1.5 m

图7. 不同潜堤个数n对聚焦波的影响，潜堤间距L_b = 2.4 m，潜堤高度H_b = 0.25 m，潜堤宽度W_b = 1.0 m

5. 结论

本文在SWASH模型的基础上，采用边界速度造波法模拟聚焦波的产生，开展了聚焦波与多个潜堤相互作用的研究，得到如下结论：

1) 潜堤高度相较于潜堤宽度对聚焦波的影响更大，随着潜堤高度以及潜堤宽度的增加，聚焦波聚焦时间以及聚焦位置会后移，同时聚焦波峰值随着潜堤宽度的增加呈现出共振的状态。潜堤之间的间距会显著影响聚焦波的能量分布，由于潜堤之间的布拉格共振作用，聚焦波峰值随着潜堤间距的变化而周期性变化，聚焦时刻和聚焦位置随着间距的增大先增加而后基本保持不变。

2) 当潜堤间距满足布拉格共振时，随着潜堤个数的增加，聚焦波峰值会明显的减小，聚焦时刻和聚焦位置后移。同时发现，若单个潜堤的共振频率和布拉格共振对应的频率相近时，当潜堤个数足够时，共振产生的高阶波将远远大于基频波浪的幅值。

3) 在实际应用中，聚焦波峰值的下降意味着波浪破坏力的下降，同时高频波相较于低频波更容易耗散以及被人们消除。研究表明，多个潜堤能够有效地抑制极端波浪的产生，在航道外设置多排潜堤，能够保护航道内船舶的航行安全，上述研究对实际工程具有重要指导意义。

基金项目

中国电力建设股份有限公司项目(DJ-ZDZX-2016-02)。

参考文献