考虑磁致伸缩效应时电机定子硅钢片的振动研究

Study on Vibration of Silicon Steel Sheet of Motor Stator Considering Magnetostrictive Effect

摘要: 为了研究交变磁场下电机定子硅钢片磁致伸缩效应的变化规律，本文首先建立了无取向硅钢片磁–机械耦合数值模型，研究了不同叠压片数无取向硅钢片在交变磁场中表面应力的变化情况，并根据仿真模型搭建了实验平台进行实验。将硅钢片水平放置在线圈一侧，并由绝缘材料固定位置，然后分别对水平放置和倾斜45˚放置的无取向硅钢片进行了应变采集和振动测量实验，结果都发现在同一交变磁场下，随着无取向硅钢片叠压片数的增加，无取向硅钢片表面的应变和振动情况逐渐减小，这与仿真结果相符。此结论对电机减振降噪有一定的指导意义。

Abstract: In order to study the variation law of magnetostrictive effect of motor stator silicon steel sheet under alternating magnetic field, the magnetic mechanical coupling numerical model of non oriented silicon steel sheet is established in this paper, and the change of surface stress of non oriented silicon steel sheet with different number of laminated sheets in alternating magnetic field is studied, and the experimental platform is built based on the simulation model. The non- oriented silicon steel sheet was placed horizontally on one side of the coil and fixed by insulating material. Then the strain collection and vibration measurement experiments were carried out on the non oriented silicon steel sheet placed horizontally and inclined 45˚ respectively. The results show that, under the same alternating magnetic field, the strain and vibration on the surface of the non oriented silicon steel sheet gradually decrease with the increase of the number of laminated sheets The true result is consistent. This conclusion has a certain guiding significance for motor vibration and noise reduction.

1. 引言

电机广泛的应用于人类生活中，尤其应用于舰船驱动等军工领域以及重工业行业等对大型电机的低噪声要求更加严格，永磁同步电机的平稳和安静运行性能在高性能应用中非常重要，例如机器人，汽车，航空和航天，所以关于抑制永磁同步电机的电磁振动噪声的研究具有重大意义。

2010年，美国学者Rakib Islam开发了一种分析模型，以径向压力作为输入来确定径向变形，通过结构有限元分析和预测径向位移加速度来对模型进行验证，计算出的径向位移用于估计不同永磁同步电机的噪音和振动 [1]。傅林提出了一种电磁振动和噪声计算的多物理场模型。通过节点力传输法，对等效的子级模型进行了模态测试，对不同电源电流下的振动和噪声进行了研究。研究发现，电流谐波对振动和噪声的影响取决于其对最低空间阶力的影响，为了找出这种效应，应考虑电流谐波的相位角、相位序列和频率 [2]。

电磁噪声的大小与定子绕组磁势空间谐波、电源中的时间谐波、转子动态偏心以及电动机的功率、极数、转速有关 [3] [4] [5] [6]。磁致伸缩力作用在铁磁材料的内部区域，由于外加磁场的作用，使得铁磁材料在磁场方向上会产生一定的变形即伸长或缩短，产生振动噪声 [7] - [12]。在永磁同步电机运行过程中，电机系统中的磁致伸缩力会导致电机定子铁心产生机械形变 [13] [14]，进而产生较大的电磁振动噪声。在电机系统中磁致伸缩力有时甚至可达到总磁力的50% [15] [16] [17] [18]，是产生电磁振动噪声的主要因素。

为了研究永磁同步电机定子硅钢片上磁致伸缩效应引起的振动噪声特性，本文首先建立了磁–机械耦合数值模型，并且根据所建的数值模型设计了一种仿真实验，来模拟永磁同步电机中的磁路走向，通电线圈与硅钢片不接触，这样无取向硅钢片上就只存在由变化磁场产生的磁致伸缩力。通过改变硅钢片与线圈的相关参数，计算得到不同情况下线圈与硅钢片的磁场分布以及硅钢片选取点的磁致伸缩应力分析，并设计实验进行测量验证。这对基于磁致伸缩下的电机减振降噪提供了参考。

2. 电磁–机械耦合数值模型

在考虑磁致伸缩效应的情况下对无取向硅钢片进行有限元计算，并建立其电磁–机械耦合数值模型，可由公式(1)和(2)表示：

$\left[S\right]\left[A\right]=\left[J_e\right]$ (1)

$\left[K\right]\left[U\right]=\left[F\right]$ (2)

式中 $J_e$ 是外部电流密度的雅可比矩阵，K表示机械刚度矩阵，S表示电磁刚度矩阵，F是作用力。通过求解得到振动位移U和矢量磁势A。

在有限元求解过程中，电磁场的求解方程为：

$\sigma \frac{\partial A}{\partial t}+\nabla \times H=J$ (3)

$B=\nabla \times A={\mu }_0{\mu }_{r}H$ (4)

$\nabla \cdot B=0$ (5)

式中 $\sigma$ 为电导率；H为磁场强度；J为外部电流密度；B为磁通密度；A为矢量磁位； ${\mu }_0$ 为真空磁导率； ${\mu }_r$ 为相对磁导率。

在对固体力学场进行分析时，固体力学场可由如下公式(6) (7)表示：

$\rho \frac{{\partial }^{2}u}{\partial t^2}-\nabla \cdot T=F\nu$ (6)

$T-T_i=C\left(S-S_i\right)$ (7)

式中，C是刚度矩阵；F是载荷量； $S_i$ 是初始应变设定值；T是所受应力； $\rho$ 代表密度； $T_i$ 是所给出的应力的初值； $\mu$ 是位移矢量；S是应变。

3. 有限元计算结果与分析

基于以上的数值模型，本文选用厚度为0.5 mm的无取向硅钢片进行了仿真实验。首先在在有限元仿真软件COMSOL Multiphysics中构建电机定子硅钢片和线圈的数值模型，设定固体力学场和磁场的各种参数，并给线圈通入50 Hz交流电用于产生交变的磁场。

3.1. 初始条件设定

硅钢片在线圈左侧水平放置，近线圈一端距离线圈10 mm，如图1所示。对线圈通入2 A的交流电，频率设定为50 Hz。

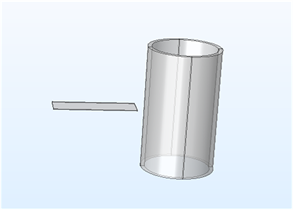
Figure 1. Position of silicon steel sheet and coil

图1. 硅钢片与线圈放置位置

本次仿真主要是对交变磁场下无取向硅钢片的磁致伸缩力进行了有限元计算，其中共进行了六组仿真，叠压片数分别为1~6片。表1为线圈和无取向硅钢片的一些参数。

Table 1. Coil and silicon steel sheet parameters

表1. 线圈与硅钢片参数

3.2. 硅钢片水平放置

首先设定好一片无取向硅钢片的位置，第2、3、4、5、6片硅钢片分别依次往上方叠加。测量点为第一片硅钢片下表面一点，如图2中红点位置所示。图3为线圈产生磁力线穿过硅钢片的过程。

Figure 2. Measuring point

图2. 测量点

Figure 3. Coil magnetic field line passing through silicon steel sheet

图3. 线圈磁场线穿过硅钢片情况

如图3所示，可以发现磁场线穿过硅钢片后磁路会发生畸变。如下图4所示分别为1~6片无取向硅钢片叠压时测量点应力的时域变化图。

(a) 1片无取向硅钢片叠压 (b) 2片无取向硅钢片叠压 (c) 3片无取向硅钢片叠压 (d) 4片无取向硅钢片叠压 (e) 5片无取向硅钢片叠压 (f) 6片无取向硅钢片叠压

Figure 4. The stress of measuring point with different number of laminations

图4. 不同叠压片数时测量点的应力

表2为图4中6种叠压情况下测量点的应力的值，此值为稳定情况下的最大值。由图4和表2可以清晰的看出随着硅钢片叠压片数的增加，最下层测量点处的应力值在不断减小，而且随着叠压片数的不断增加，测量点的应力减小幅度变得缓慢。

Table 2. The stress values of the measuring points with different number of laminations

表2. 不同叠压片数时测量点的应力值

4. 无取向硅钢片应变和振动测量实验

为了验证上述仿真结果，本文搭建了线圈与无取向硅钢片的实验平台。给线圈绕组中通入50 Hz的工频交流电产生交变磁场，利用JHDY动态应变测量系统和三片直角型应变片采集硅钢片上的应变情况。利用振动测量仪HEAD acoustics Squadriga II和加速度传感器测量交变磁场中的振动信号并在振动测量仪中对振动信号解析和存储。

4.1. 应变测量实验

首先打开JHDY动态应变测量系统的电脑端与设备相连接，并将采样频率设定为1000 Hz，在线圈未通电时对数据进行示波不保存，然后进行调零消除环境的影响，再通电进行测量并保存数据。

如图5所示为所测量最下层无取向硅钢片上一点的应变值，测量片数分别为1~6片。在改变叠压片数的同时要保证放置位置不被改变，这样才能进一步的控制变量，增加实验的准确性。

表3为叠压片数为1~6片的无取向硅钢片应变测量峰值，从表3中可以看出随着硅钢片片数的增加，测量点的应变值在不断的减小，与在有限元中测量的结果规律相符。

(a) 1片无取向硅钢片叠压 (b) 2片无取向硅钢片叠压 (c) 3片无取向硅钢片叠压 (d) 4片无取向硅钢片叠压 (e) 5片无取向硅钢片叠压 (f) 6片无取向硅钢片叠压

Figure 5. Strain of measuring point with different number of laminations

图5. 不同叠压片数时测量点的应变

Table 3. Strain values of measuring points with different number of laminations

表3. 不同叠压片数时测量点的应变值

4.2. 振动测量实验

为了进一步验证交变磁场中不同叠压片数硅钢片振动情况，本节中将45˚倾斜放置的无取向硅钢片置于交变磁场中，并进行了振动测量实验。

根据以上搭建的振动测量平台对不同叠压片数的无取向硅钢片进行振动测试实验，分别对1-6片无取向硅钢片叠压并45˚倾斜放置时的振动信号进行了测量，实验结果如下图6所示。

如图6所示，为45˚倾斜放置时不同叠压片数无取向硅钢片在交变磁场中的振动情况，实验数据截取0.05 s的数值。如下表4所示，为不同叠压片数硅钢片的振动峰值。

(a) 1片无取向硅钢片叠压 (b) 2片无取向硅钢片叠压 (c) 3片无取向硅钢片叠压 (d) 4片无取向硅钢片叠压 (e) 5片无取向硅钢片叠压 (f) 6片无取向硅钢片叠压

Figure 6. Vibration signals of stator silicon steel sheets with different number of laminations placed at 45˚ in alternating magnetic field

图6. 交变磁场中不同叠压片数定子硅钢片45˚放置时的振动信号

结合表4中不同叠压片数硅钢片在交变磁场中的振动幅值和图6中不同叠压片数硅钢片的振动波形，可以发现在同一交变磁场中，随着硅钢片叠压片数的增加，硅钢片整体的振动在减小。结果同应变实验和有限元仿真中的结果全部相符。

Table 4. Vibration of silicon steel sheet placed at 45 degrees

表4. 硅钢片45˚放置时振动情况

结合表2、表3和表4的三组数据(交变磁场中应变形成的同时，硅钢片表面出现振动和内部应力)，可以发现无论是对硅钢片进行有限元中仿真的结果还是对硅钢片进行应变实验和振动实验的结果，都表明了在交变磁场中随着无取向硅钢片叠压片数的增加，无取向硅钢片表面由磁致伸缩效应导致的形变和振动会减小。

5. 结论

本文在交变磁场中对电机定子无取向硅钢片进行有限元仿真，发现在同一交变磁场下，随着无取向硅钢片叠压片数的增加，其表面由磁致伸缩导致的应力会逐渐地减小。

为了对此结论进行验证，进一步搭建了无取向硅钢片的应变测试平台和振动测量平台，分别对水平放置和倾斜放置的无取向硅钢片进行了应变测量和振动测量，结果显示在交变磁场中随着无取向硅钢片叠压片数的增加，应变片采集到的应变数值和振动测量仪采集到的振动数值都在不断地减小，而且减小的幅度也在逐渐减小。此结论与仿真相符。这对研究永磁同步电机的振动源有重要的参考价值。

基金项目

感谢国家自然科学基金(51577131)和天津市自然科学基金面上项目(20JCYBJC00190)资助。