(2 + 1)维变系数Broer-Kaup方程的精确解与局域激发

Exact Solution and Local Excitation of (2 + 1)-Dimensional Variable Coefficient Broer-Kaup Equation

摘要: 利用拓展的Riccati映射法对2 + 1维变系数BK方程进行了分析，得到了包含任意函数的精确解，通过对任意函数进行选取，得到了相关的局域激发结构。此方法在求解其他非线性偏微分方程上也有广泛应用。

Abstract: The extended Riccati mapping method is used to analyze the 2 + 1 dimensional variable coefficient Broer-Kaup equation, and the exact solution containing any function is obtained. By selecting the arbitrary function, the relevant local excitation structure is obtained. This method is also widely used in solving other nonlinear partial differential equations.

1. 引言

在实际生活中，很多的物理现象都可以用数学模型来描述，这些模型往往是非线性的，因此研究非线性偏微分方程的精确解，以及解的相关性质是非线性理论科学的重要研究内容。近年来，出现了很多

简单有效的求解非线性系统精确解的方法，如齐次平衡法、 $\frac{G^{\prime }}{G}$ 展开法、Jacobi椭圆函数展开法、Riccati映射

法、Tanh展开法等 [1] [2] [3]。非线性偏微分方程的精确解中含有相关变量的任意函数，通过对任意函数的选取，能够获得相应非线性系统的局域激发，从而对部分物理现象做出解释。本文通过应用Riccati映射法，选取一类Riccati方程作为辅助方程，将原有的行波变换扩展为包含任意函数的变换，从而获得2 + 1维变系数Broer-Kaup方程的含有任意函数的非行波精确解，并选取合适函数，获得局域激发结构。

考虑2 + 1维变系数Broer-Kaup方程

$u_{yt}-\alpha \left(t\right)\left[u_{xxy}-2{\left(u{u}_x\right)}_y-2v_{xx}\right]=0$

$v_t+\alpha \left(t\right)\left[v_{xx}+2{\left(uv\right)}_x\right]=0$ (1.1)

在非线性领域有着广泛的应用，其中 $\alpha \left(t\right)$ 是t的函数。 $\alpha \left(t\right)=1$ 时，(1.1)化为常系数2 + 1维Broer-Kaup方程， $\alpha \left(t\right)=-1$ 时，(1.1)化为修正的色散长水波方程，文献 [3] 借助Riccati方程对(1.1)进行了求解，并获得了局域激发。文献 [4] 利用齐次平衡法对(1.1)进行了求解，获得了新的类孤子解，有很多文献对2 + 1维变系数Broer-Kaup方程的精确解及局域激发进行了研究 [5] - [14]。

2. 拓展的Riccati展开法解法概述

给定一个非线性系统

$P\left(u,u_t,u_x,u_{xx}{u}_{xt},\cdots \right)$ (2.1)

设它的解有如下形式

$u={\displaystyle \underset{i=-n}{\overset{n}{\sum }}{a}_i\left(x\right){\varphi }^i\left(q\right)}$ (2.2)

其中q满足

${\varphi }^{\prime }=\sigma +{\varphi }^2$ (2.3)

(2.3)解的情况如下

$\begin{array}{l}\varphi =\sqrt{\sigma }\tan \left(\sqrt{\sigma }q\right)\sigma >0\\ \varphi =-\sqrt{\sigma }\cot \left(\sqrt{\sigma }q\right)\sigma >0\end{array}$

$\begin{array}{l}\varphi =-\sqrt{-\sigma }\tanh \left(\sqrt{-\sigma }q\right)\sigma <0\\ \varphi =-\sqrt{-\sigma }\coth \left(\sqrt{-\sigma }q\right)\sigma <0\end{array}$

$\varphi =-1/q\sigma =0$ (2.4)

其中 $x=\left(x_0,x_1\cdots ,x_m\right)$， $a_i\left(x\right)$ 为待求函数， $q=q\left(x\right)$ 为任意函数， $\sigma$ 为任意常数，n根据齐次平衡法确定。将(2.2)、(2.3)代入(2.1)，合并 ${\varphi }^i$ 的同类项，并取同幂次系数为零，得到一组关于 $a_i\left(x\right)$， $q=q\left(x\right)$ 的偏微分约束方程组，解出 $a_i\left(x\right)$， $q=q\left(x\right)$，代入(2.2)结合(2.4)就可以得到所求方程的精确解。

3. 2 + 1维变系数BK方程的精确解

为了方便求解，对(1.1)作变换

$v=u_y$ (3.1)

将(3.1)代入(1.1)可以将(1.1)化为

$u_{yt}+\alpha \left(t\right)\left[2{\left(u{u}_x\right)}_y+u_{xxy}\right]=0$ (3.2)

根据齐次平衡法，(3.2)有如下形式的解

$u=f+g\varphi \left(q\right)+h{\varphi }^{-1}\left(q\right)$ (3.3)

其中f，g，h，q是关于 $\left(x,y,t\right)$ 的任意函数。将(3.3)、(2.3)代入(3.2)，合并 ${\varphi }^i$ 的同次幂，并取 ${\varphi }^i$ 的系数为零，得到一个关于f，g，h，q的偏微分方程组，求解得

$f=-\frac{\alpha \left(t\right)q_{xx}+q_t}{2q_x\alpha \left(t\right)}$， $g=-q_x$， $h=q_x\sigma$ (3.4)

在求解上述偏微分方程组的过程中，通过将(3.4)代入方程组约化发现，约化后关于q的方程组有一个特解

$q\left(x,y,t\right)=\chi \left(x,t\right)+\phi \left(y\right)$ (3.5)

将(2.4)、(3.4)、(3.5)代入(3.3)并结合(3.1)得到2 + 1维变系数Broer-Kaup方程的精确解

情形1 当 $\sigma <0$ 时

$u_1=-\frac{\alpha \left(t\right){\chi }_{xx}+{\chi }_t}{2{\chi }_x\alpha \left(t\right)}+{\chi }_x\cdot \sqrt{-\sigma }\tanh \left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)-{\chi }_x\sigma \cdot {\left(\sqrt{-\sigma }\tanh \left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)\right)}^{-1}$ (3.6)

$v_1=-{\chi }_x\sigma {\phi }^{\prime }\left({\text{sech}}^2\left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)-\frac{{\text{sech}}^2\left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)}{{\tanh }^2\left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)}\right)$ (3.7)

$u_2=-\frac{\alpha \left(t\right){\chi }_{xx}+{\chi }_t}{2{\chi }_x\alpha \left(t\right)}+{\chi }_x\cdot \sqrt{-\sigma }\cdot \coth \left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)-{\chi }_x\sigma \cdot {\left(\sqrt{-\sigma }\cdot \coth \left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)\right)}^{-1}$ (3.8)

$v_2={\chi }_x\sigma {\phi }^{\prime }\left({\text{csch}}^2\left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)-\frac{{\text{csch}}^2\left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)}{{\coth }^2\left(\sqrt{-\sigma }\left(\chi +\phi \right)\right)}\right)$ (3.9)

情形2 当 $\sigma >0$ 时

$u_3=-\frac{\alpha \left(t\right){\chi }_{xx}+{\chi }_t}{2{\chi }_x\alpha \left(t\right)}-{\chi }_x\cdot \sqrt{\sigma }\tan \left(\sqrt{\sigma }\left(\chi +\phi \right)\right)+{\chi }_x\sigma \cdot {\left(\sqrt{\sigma }\tan \left(\sqrt{\sigma }\left(\chi +\phi \right)\right)\right)}^{-1}$ (3.10)

$v_3=-{\chi }_x\sigma {\phi }^{\prime }\left({\sec }^2\left(\sqrt{\sigma }\left(\chi +\phi \right)\right)+\frac{{\sec }^2\left(\sqrt{\sigma }\left(\chi +\phi \right)\right)}{{\tan }^2\left(\sqrt{\sigma }\left(\chi +\phi \right)\right)}\right)$ (3.11)

$u_4=-\frac{\alpha \left(t\right){\chi }_{xx}+{\chi }_t}{2{\chi }_x\alpha \left(t\right)}+{\chi }_x\cdot \sqrt{\sigma }\cot \left(\sqrt{\sigma }\left(\chi +\phi \right)\right)-{\chi }_x\sigma \cdot {\left(\sqrt{\sigma }\cot \left(\sqrt{\sigma }\left(\chi +\phi \right)\right)\right)}^{-1}$ (3.12)

$v_4=-{\chi }_x\sigma {\phi }^{\prime }\left({\csc }^2\left(\sqrt{\sigma }\left(\chi +\phi \right)\right)+\frac{{\csc }^2\left(\sqrt{\sigma }\left(\chi +\phi \right)\right)}{{\cot }^2\left(\sqrt{\sigma }\left(\chi +\phi \right)\right)}\right)$ (3.13)

情形3 $\sigma =0$ 时

$u_5=-\frac{\alpha \left(t\right){\chi }_{xx}+{\chi }_t}{2{\chi }_x\alpha \left(t\right)}+{\chi }_x\cdot \frac{1}{\chi +\phi }-{\chi }_x\sigma \cdot \left(\chi +\phi \right)$ (3.14)

$v_5=-{\chi }_x\cdot \frac{{\phi }^{\prime }}{{\left(\chi +\phi \right)}^2}-{\chi }_x\sigma \cdot {\phi }^{\prime }$ (3.15)

以上的 $\chi =\chi \left(x,y,t\right)$， $\phi =\phi \left(y\right)$。

4. 局域激发与分形结构

选取一种简单的情形

$\chi \left(x,t\right)=-x^2+t^2$， $\phi \left(y\right)=-y^2$ (3.16)

将(3.16)代入(3.7)，取 $\sigma =1$， $t=4$，可以得到环孤子，如图1，将(3.16)代入(3.6)，取 $\sigma =1$， $\alpha \left(t\right)=1$， $t=0$ 可以得到2dromin解，如图2，在图2的基础上，依次选取 $x\in \left[-1\times {10}^{-6},1\times {10}^{-6}\right]$， $y\in \left[-1\times {10}^{-6},1\times {10}^{-6}\right]$ 得到图3， $x\in \left[-1\times {10}^{-9},1\times {10}^{-9}\right]$， $y\in \left[-1\times {10}^{-9},1\times {10}^{-9}\right]$ 得到图4。可以发现，无论怎么缩小，图2依旧保持规则的分形结构。

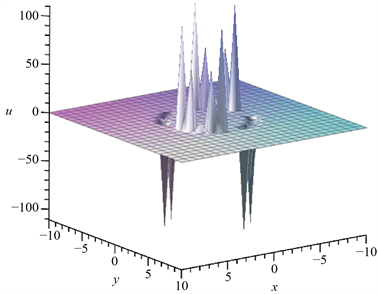
Figure 1. The ring soliton structure is obtained when $t=4$, $\sigma =1$

图1. 取 $t=4$， $\sigma =1$ 时得到的环状孤子结构

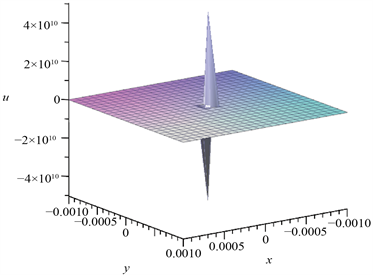
Figure 2. Take $t=0$, $\sigma =1$ Take to get the light and dark domion

图2. 取 $t=0$， $\sigma =1$ 时得到的亮暗domion

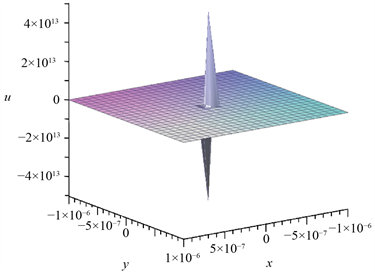
Figure 3. Figure 2 takes $x,y\in \left[-1\times {10}^{-6},1\times {10}^{-6}\right]$

图3. 图2取 $x,y\in \left[-1\times {10}^{-6},1\times {10}^{-6}\right]$

Figure 4. Figure 2 takes $x,y\in \left[-1\times {10}^{-9},1\times {10}^{-9}\right]$

图4. 图2取 $x,y\in \left[-1\times {10}^{-9},1\times {10}^{-9}\right]$

5. 结论

本文用拓展的Riccati映射法求解了2 + 1维变系数Broer-Kaup方程，得到了5组含有任意函数的精确解，通过对任意函数的选取，可以得到丰富的局域结构，给出了一个简单的选取示例，得到了环孤子结构和一种分形结构。拓展的Riccati映射法还可以用来求解其他的非线性偏微分方程。