1. 引言
计算机视觉研究的目的是为了让计算机通过二维图像来认知三维世界,从此过程中获得信息应用于物体识别或三维重建等研究领域。而相机便是二维图像与三维空间之间的一种映射模型,所以相机标定方法的研究作为计算机视觉的先决条件显得十分重要。
相机标定是机器视觉、摄影测量和计算机视觉等应用的核心步骤,它在机器人、导航系统和航空系统等领域中都具有重要的意义,相关文献中提出了众多不同相机标定的方法,但每种方法都有它适用的应用场景,每种方法都有它的优缺点 [1]。随着计算机视觉的不断发展,快速、简捷且具有一定精度的相机标定算法正在深入的研究中。相机标定方法可根据不同的分类标准进行分类,例如把划分的标准定为标定物种类的话,相机标定方法可分为平面标定和立体标定;例如把划分的标准定为成像模型的话,可分为线性标定和非线性标定;若把划分标准定为标定方式,可分为传统相机标定、基于主动视觉的相机标定和相机自标定方法 [2]。在对视觉系统的精度有较高要求的场景,通常需要借助几何尺寸已知的标定模板完成相机的标定过程 [3] - [9]。其中较为经典的Z. Zhang [10] 的标定方法便借助一个标准的棋盘格,假设标定所用的平面网格模板在世界坐标系中
平面上,使用相机从各个角度拍摄这副棋盘格,提取图像中棋盘格的角点,最后通过角点的坐标以及世界坐标系下角点坐标的映射关系,计算出相机的内外参数,从而完成相机标定。
本文受Z. Zhang [10] 的标定方法的启发,结合相机传统标定方法和自标定方法的优势,目的在于测试用人脸关键点作为标定对象的可能性,通过对采集到的随机人脸图像进行基本的图像预处理,采用人脸关键点检测框架提取人脸关键点作为特征点,根据特征点的坐标信息和其对应的三维空间面点,计算单应性矩阵来标定相机,得到相机的内方位元素,同样通过检测图像中的人脸关键点来计算相机的外方位元素,这种方法有效地提高了相机标定结果的精度。
2. 人脸关键点检测
人脸面部包含许多的有用关键点信息,关键点的检测可用于人脸姿态识别与矫正等应用场景 [11],人脸关键点的检测是人脸识别和分析领域中基础且非常关键的一环,是人脸识别、三维人脸重建、表情分析等人脸相关研究的突破口。这一步的目的是为了实现人脸关键点的检测并得到其坐标信息,为后续的相机标定做好准备工作。使用Dlib模块来检测图像中的人脸,自动检测出图像中的人脸,实现68个人脸关键点的高精度定位。在此模块中,随机输入一张经过图像预处理的人脸图像,将其作为标定对象,通过Dlib库中自带的人脸检测器和关键点特征提取器来检测人脸框的四个角点和68个人脸关键点的坐标,然后对相机进行标定。
预处理是人脸识别和关键点检测过程的一个重要环节,在采集图像时,由于拍摄环境、光照程度以及成像设备的特性等因素,会存在有噪声、对比度不够等缺点,为了保证人脸图像的质量,在视觉上更加清晰,更利于计算机的处理和识别,须对图像进行预处理操作。本文实验的预处理主要包括人脸图像的灰度矫正、噪声过滤和归一化操作。灰度矫正采用了直方图均衡方法逐点改变图像的灰度值,使得各个灰度级的像素点数量相等,使直方图平衡化;噪声过滤使用了非线性的中值滤波器去除噪声,在一定程度上可以保持人脸轮廓的边缘性,不会有显著的模糊产生;归一化操作通过几何归一化来保证人脸尺度的一致性,再通过灰度归一化来减弱由不同光照强度和方向下引起的图像信号变化,
Dlib是一个开源的机器学习库,包含了许多的机器学习的算法和工具,可广泛适用于很多场景,目前Dlib已经广泛应用在机器人、嵌入式计算环境等各个领域,它实现了文献 [12] 中的算法,Dlib库的人脸检测标记算法十分准确。它的核心原理是先检测到人脸,需要用大小位置不同的窗口在图像中滑动,判断窗口中是否存在人脸,使用图像HOG (Historgram of Oriented Gradient)特征来表示人脸,HOG特征是一种在图像局部方格单元上操作的纹理特征,本质为梯度的信息统计,它在图像几何和光学形变上具有很好的不变性,特别适合应用于图像中的人体检测。最后结合支持向量机 [13] (Support Vector Machine)的方法实现人脸检测的功能,得到人脸检测框的四个角点的坐标信息。然后进入人脸识别阶段,通过适用于人脸的深度残差网络 [14] (Residual Network)提取人脸特征向量,得到嘴角、眼睛边等人脸各部位点的坐标信息,即实现了如图1所示的68个特征点的检测。
在本文的实验中,这一步骤的目的不是构建网络结构,而是获得人脸关键点的特征信息,为后续的标定工作做准备,所以直接使用Dlib库中提供的人脸检测方法,对带有人脸的图像进行滑动扫描,提取HOG特征,并用深度残差网络实现人脸关键点检测。如果检测到人脸,则将其标定出来,并自动标出人脸上眼睛鼻子嘴巴和脸轮廓等标志性特征位置。人脸关键点检测的主要内容包含人脸检测和68个关键点的标定,流程主要为图2所示。
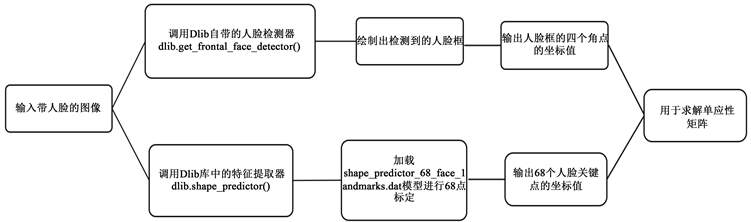
Figure 2. Face key point detection flow chart
图2. 人脸关键点检测流程图
3. 相机标定法
3.1. 求解单应性矩阵
在相机的成像模型中,所用到的四个坐标系分别是图像像素坐标系、图像成像坐标系、相机坐标系和世界坐标系。相机标定的过程一般是从世界坐标系转换为相机坐标系,再从相机坐标系转换为图像像素坐标系,由于图像像素坐标系不利于坐标转换,需要建立图像成像坐标系。假设在三维空间中有一点P的世界坐标系的齐次坐标是
,它投影到二维图像中对应点的像素坐标为
,这四个坐标系之间的转换即从世界坐标系到图像坐标系的坐标映射关系为
(1)
其中
,
分别为像素单位的X轴和Y轴方向上的焦距,一般情况下二者相等或近似,
为图像的主点坐标,R和t分别是相机拍摄图像时的旋转矩阵和平移向量,也就是外方位元素。
而我们将人脸作为二维平面对象,在相机模型下,对于二维平面表面,三维到二维的投影关系可以简化为二维到二维的转换,因此,假设包含此二维平面的相机模型平面在世界坐标系的
上,在这样的假设下,一张人脸上的三维点就变成了一个二维平面点,利用单应性变换,可以将这个二维平面点投影到二维图像平面中,投影关系为:
(2)
其中
是比例因子,H是需要求解的3 × 3的单应性矩阵,可以推算为:
(3)
由公式(3)可以看出单应性矩阵H同时包含相机的内方位元素和外方位元素,即K是需要求解的内方位元素矩阵:
(4)
而
称为相机的外方位元素矩阵,
(5)
最后通过公式(4)和公式(5)的换算可以得到公式(2):
(6)
为了标定出相机的内外方位元素,首先根据人脸关键点检测出的特征点的坐标信息结合公式(2)计算出单应性矩阵H,然后根据公式(3)计算出所需的内方位元素矩阵和外方位元素矩阵,从而完成相机标定。一般在计算单应性矩阵的过程中只需要四个对应点的坐标信息,由于我们运用的人脸关键点检测算法最多能够检测到人脸的68个关键点,完全满足了求解单应性矩阵的条件。
3.2. 计算相机内外方位元素
在此方法中,假设不存在旋转和平移的情况,那么相机的内方位元素矩阵K就是前面求解的单应性矩阵H:
(7)
即
,在得到相机的内方位元素矩阵后,矩阵中求解到的焦距是一个理想焦距,并不是相机镜头的实际焦距值,需要利用相机的像元大小来计算相机的焦距(以毫米为单位),而像元大小是指一个像素在X和Y方向上所代表的实际大小,因此需要通过公式(8)求解最后的焦距值。
(8)
最后通过得到的内方位元素矩阵和公式(6)计算相机的外方位元素:
(9)
(10)
其中
是由比例因子s来定义的,旋转矩阵
的计算公式为:
平移向量t的计算公式为:
(14)
至此,相机的内方位元素和外方位元素都求解出来了。最后用重投影法作为对标定结果进行评估的方法,它可以有效的反映出相机标定参数的精度及相机标定算法的好坏。用标定出来的结果计算每个角点在反方向上投影所得的像点坐标,再与实际检测到的像点坐标作差,得到总平均误差 [15]。重投影法公式为:
(15)
(16)
(17)
Q表示重投影点坐标和实际检测的角点坐标的向量差,S代表这两个点的标量距离。若在一幅图像中检测到多个角点时,便对每个角点都进行重投影,分别求得标量距离Si,再进行均值处理,即可获得一幅图像的平均误差来评价标定结果,平均重投影误差越接近零,则表示相机标定的精度越高。
4. 标定结果与分析
实验的目的是为了验证使用人脸的关键点作为特征点进行相机标定这一想法的可行性,将提出的方法的实验结果与Z. Zhang [10] 的棋盘格图作为二维标定对象的标定方法进行了比较。本文所使用的数据集是通过自制CMOS相机采集的,图像采集可在室外或室内的可控环境中进行,我们为三个不同的对象采集一组(8到12张)人脸图像,在光线均匀明亮的环境中,分别从不同的高度和距离对人脸进行平行没有旋转的拍摄,拍摄的.bmp图片都具有固定的图像分辨率和焦距。图片经过灰度矫正、噪声过滤及归一化等图像预处理方法后,添加到本文标定程序文件夹下,分别检测获得人脸框的四个角点和68个人脸关键点的坐标信息,通过这两种方式来标定相机,如图3所示,对每个标定对象分别进行实验,完成相机标定。得到图像的像素平均误差如表1所示。


Table 1. The average pixel error of camera calibration results
表1. 相机标定结果的图像像素平均误差
分别表示两种不同标定方法与张氏标定法实验结果的图像像素误差,通过实验结果可得,将人脸图像作为标定模板,检测得到人脸框的四个角点的坐标信息,对CMOS相进行相机标定,平均重投影误差约为
;在使用同一组人脸图像的情况下,检测得到68个人脸关键点的坐标信息对相机进行标定,平均重投影误差为
。由此可见,关键点越多并且均匀分布在图像中的时候,标定精度更高。而在相同的条件下,在不同的相对位置拍摄三组统一棋盘格标定模板图片,如图4,通过Bouguet [16] 参照Z. Zhang [10] 标定法编写的Matlab相机标定工具箱,完成张正友标定法,作为对比实验。所得的标定结果如图5所示。

Figure 4. Part of the checkerboard image experiment image
图4. 部分棋盘格图像实验图像
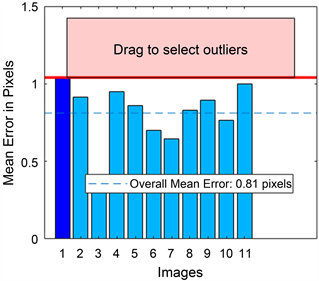
Figure 5. Histogram of pixel mean error of Matlab Toolbox calib
图5. Matlab标定工具箱的像素平均误差直方图
总体图像像素平均误差
。张氏标定法是介于传统相机标定方法和相机自标定方法之间的一种经典方法,可以作为正确性的比较标准,由对比实验结果可知,本文提出的相机标定算法取得的标定精度优于张氏标定法,误差较小,标定精度更高,且标定过程较简便,只需要一组带有人脸的图像即可进行相机标定,成功验证了使用人脸图像中的人脸关键点标定相机方法的可行性。相较于二维精密转台和平行光管的光学实验室标定方法更加简便快捷。
5. 结束语
本文的研究方法基于Z. Zhang [10] 的标定方法,并结合了传统相机标定方法和自标定方法的优势,提出了一个新的标定方法,使用人脸关键点来标定相机,并通过重投影的方法对标定结果进行评估。根据提出的方法,用相机拍摄的随机人脸图像作为二维的标定对象,检测出人脸图像中的关键点并提取它们的坐标信息,求取单应性矩阵,最后求取相机的内方位元素和外方位元素,分析实验结果。标定的精度与Z. Zhang [10] 的标定方法(已被验证为迄今最有效的二维标定方法)相比较,实验结果表明,本文的相机标定算法提高了标定精度和稳定性且标定过程更简单。
参考文献