一类快慢耦合Duffing-van der Pol系统的平衡点分析
Equilibrium Analysis of a Class of Fast-Slow Coupled Duffing-van der Pol System
DOI: 10.12677/DSC.2021.102010, PDF, HTML, XML,    国家自然科学基金支持
作者: 张丹瑾, 钱有华*：浙江师范大学，数学与计算机科学学院，浙江 金华
关键词: Duffing-van der Pol系统；一元五次方程；降次解法；盛金公式；Duffing-van der Pol System； Quintic Equation of One Variable； The Method of Reducing the Order for Solving； Morigane Formula
摘要: 本文主要研究了一类5次项和3次项共存的快慢耦合Duffing-van der Pol系统的平衡点问题。对系统求平衡点，得到了一个一元五次方程。使用一元次方程的降次解法，将平衡点方程的五次降到四次。当平衡点方程降到四次时，计算得到常数项的系数为零，所以可以直接降次为三次方程。采用盛金公式来对三次方程进行分类求解。综合这四类情形，得到了平衡点方程的解在F-u1平面上的个数分布。
Abstract: This paper studies the equilibrium point problem of a class of fast-slow coupled Duffing-van der Pol system with the coexistence of quintic term and cubic term. Quintic equation of one variable is obtained by solving the equilibrium points of the system. By using the method of reducing the order of n degree equation of one variable, the order of the equilibrium equation is reduced from five to four. When the equilibrium equation is reduced to the quartic, the coefficient of the constant term is calculated to be zero, so it can be directly reduced to the cubic equation. Morigane formula is used to solve the cubic equation. The distribution of the solution of the equilibrium equation on the F-u1 plane is obtained by synthesizing these four cases.
文章引用：张丹瑾, 钱有华. 一类快慢耦合Duffing-van der Pol系统的平衡点分析[J]. 动力系统与控制, 2021, 10(2): 91-99. https://doi.org/10.12677/DSC.2021.102010

1. 引言

Duffing方程和van der Pol方程都是典型的非线性振动系统，已有不少学者对这两类方程的动力学行为进行研究 [1] - [6]。本文主要研究了一类5次项和3次项共存的快慢耦合Duffing-van der Pol系统的平衡点 [7] [8] 问题。我们在分析平衡点时，会遇到一元n次方程。

对于一元n次方程求解问题 [9] [10] [11] [12]，人们从很早之前就已经有所研究。在9世纪时，阿拉伯人花剌子模第一次给出了一元二次方程的一般解法。在16世纪时，意大利数学家塔尔塔利亚和卡尔达诺等人发现了一元三次方程的求根公式，费拉里找到了四次方程的求根公式。在此之后近三个世纪，对于五次及以上高阶方程，莱布尼茨(Leibniz)、范德蒙德(Vandermonde)、拉格朗日(Lagrange)等人一直在寻找这样的求根公式。直到19世纪，挪威学者阿贝尔(Abel)终于证明了：一般的 n ≥ 5 次方程不可能用根式求解，即不存在根式表达的一般五次方程求根公式。在20世纪时，中国学者范盛金深入探讨了对一元三次方程的求解问题，推导出了一套新的求根公式—盛金公式 [13]，并建立了一种新的判别法—盛金判别法。

本文采用一元n次方程的降次解法，分析了一类5次项和3次项共存的快慢耦合Duffing-van der Pol系统的平衡点问题。先对系统求平衡点，得到一元五次方程。再使用一元n次方程的降次解法，将五次方程降到三次。接着采用盛金公式对三次方程求解。最后综合四类情形，得到平衡点方程的解在F-u1平面上的分布。

2. 数学模型与平衡点方程

在文献 [14] 中，刘延彬和陈予恕考虑了一类5次项和3次项共存的Duffing-van der Pol方程的余维4系统：

{ x ˙ = y , y ˙ = u 1 x + u 2 y + x 3 + x 5 + a x 2 y + b x 4 y . (1)

在此基础上，我们引入了一个外周期激励项，形成一个新的二维非自治系统：

{ x ˙ = y , y ˙ = u 1 x + u 2 y + x 3 + x 5 + a x 2 y + b x 4 y + f cos ω t , (2)

其中 f cos ω t 为激励项(f为幅值， ω 为频率)。定义 F = f cos ω t ，则系统(2)可转换为：

{ x ˙ = y , y ˙ = u 1 x + u 2 y + x 3 + x 5 + a x 2 y + b x 4 y + F . (3)

当激励项的频率 ω 和系统的固有频率 Ω 之间存在一定的量级差异时，系统存在不同时间尺度效应。所以我们取定 ω ≪ 1 ，显然系统存在两个时间尺度的快慢耦合。在固有频率对应的任一周期 t ∈ [ t 0 , t 0 + 2 π / Ω ] 内，周期激励项 F = f cos ω t 在 Ω A = f cos ( ω t 0 ) 和 Ω B = f cos ( ω t 0 + 2 π ω / Ω ) 之间变化，显然 Ω A ≈ Ω B ，这可以看出F在固有频率的任一周期内的变化非常小。所以我们可以将整个周期激励项F看作一个慢变参数，相应地，可称系统(3)为包含慢变参数F的广义自治系统。此时，我们将广义自治系统(3)看作是快变量x，y对应的快子系统，而 F = f cos ω t 可看作是相应的慢子系统。

下面，对系统(3)求平衡点，得到了方程(4)：

{ y = 0 , u 1 x + x 3 + x 5 + F = 0. (4)

所以我们接下来要计算五次方程：

x 5 = − x 3 − u 1 x − F . (5)

3. 一元 次方程的降次解法分析

下面我们将根据文献 [10] 中的一元n次方程的降次解法来求解五次方程(5)。首先，我们将五次方程转化为五阶常系数齐次线性微分方程，接着将其降次为四次方程来求解。

对于五次方程(5)，对应的常系数齐次线性微分方程为

y ( 5 ) = − y ( 3 ) − u 1 y ( 1 ) − F y . (6)

由欧拉特征根法可得(6)的指数解为 e ξ t ，其中 ξ 为方程(5)的根。

由高阶线性微分方程的一般解法得到(6)的多重积分级数通解为

y ( t ) = ∑ j = 1 5 C j Y j ( t ) , (7)

其中 C j ( j = 1 , 2 , ⋯ , n ) 为任意常数，

Y j ( t ) = t j − 1 + ∑ m = 1 ∞ ∫ 0 t ( − y j ( m − 1 ) ( 3 ) − u 1 y j ( m − 1 ) ( 1 ) − F y j ( m − 1 ) ) ( d t ) 5 5 ( j = 1 , 2 , ⋯ , n ) . (8)

因而

e ξ t = ∑ j = 1 5 C j Y j ( t ) . (9)

把 t = 0 、 t = 1 、 t = 2 、 t = 3 和 t = 4 代入方程9，得到

C 1 = 1 , e ξ = ∑ j = 1 5 C j Y j ( 1 ) , ⋯ , e 4 ξ = ∑ j = 1 5 C j Y j ( 4 ) . (10)

通过计算，可得

Y 1 ( 1 ) = 1 + ( − F ) + ( − F ) 2 + ⋯ + ( − F ) m + ⋯ = 1 − F lim m → ∞ [ 1 − ( − F ) m ] 1 + F (11)

Y 2 ( 1 ) = 1 + ( − u 1 − 1 2 F ) + ( − u 1 − 1 2 F ) ( − F ) + ⋯ + ( − u 1 − 1 2 F ) ( − F ) m − 1 + ⋯ = 1 − ( − u 1 − 1 2 F ) Y 1 ( 1 )

⋮

通过一元五次方程的降次解法，计算得到

b 0 = 2 [ Y 2 ( 1 ) Y 3 ( 1 ) Y 4 ( 2 ) Y 5 ( 3 ) − Y 2 ( 1 ) Y 3 ( 1 ) Y 5 ( 2 ) Y 4 ( 3 ) + Y 2 ( 1 ) Y 5 ( 1 ) Y 3 ( 2 ) Y 4 ( 3 )     − Y 2 ( 1 ) Y 5 ( 1 ) Y 4 ( 2 ) Y 3 ( 3 ) − Y 3 ( 1 ) Y 4 ( 1 ) Y 2 ( 2 ) Y 5 ( 3 ) + Y 3 ( 1 ) Y 4 ( 1 ) Y 5 ( 2 ) Y 2 ( 3 )     + Y 4 ( 1 ) Y 5 ( 1 ) Y 2 ( 2 ) Y 3 ( 3 ) − Y 4 ( 1 ) Y 5 ( 1 ) Y 3 ( 2 ) Y 2 ( 3 ) ] ,

b 1 = 2 b 0 [ Y 3 ( 1 ) Y 2 ( 2 ) Y 4 ( 3 ) Y 5 ( 4 ) − Y 3 ( 1 ) Y 2 ( 2 ) Y 5 ( 3 ) Y 4 ( 4 ) − Y 3 ( 1 ) Y 4 ( 2 ) Y 2 ( 3 ) Y 5 ( 4 )     + Y 3 ( 1 ) Y 4 ( 2 ) Y 5 ( 3 ) Y 2 ( 4 ) + Y 3 ( 1 ) Y 5 ( 2 ) Y 2 ( 3 ) Y 4 ( 4 ) − Y 3 ( 1 ) Y 5 ( 2 ) Y 4 ( 3 ) Y 2 ( 4 )     + Y 5 ( 1 ) Y 2 ( 2 ) Y 3 ( 3 ) Y 4 ( 4 ) − Y 5 ( 1 ) Y 2 ( 2 ) Y 4 ( 3 ) Y 3 ( 4 ) − Y 5 ( 1 ) Y 3 ( 2 ) Y 2 ( 3 ) Y 4 ( 4 )     + Y 5 ( 1 ) Y 3 ( 2 ) Y 4 ( 3 ) Y 2 ( 4 ) + Y 5 ( 1 ) Y 4 ( 2 ) Y 2 ( 3 ) Y 3 ( 4 ) − Y 5 ( 1 ) Y 4 ( 2 ) Y 3 ( 3 ) Y 2 ( 4 ) ] ,

b 2 = 2 b 0 [ Y 2 ( 1 ) Y 3 ( 1 ) Y 4 ( 3 ) Y 5 ( 4 ) − Y 2 ( 1 ) Y 3 ( 1 ) Y 5 ( 3 ) Y 4 ( 4 ) + Y 2 ( 1 ) Y 5 ( 1 ) Y 3 ( 3 ) Y 4 ( 4 )     − Y 2 ( 1 ) Y 5 ( 1 ) Y 4 ( 3 ) Y 3 ( 4 ) − Y 3 ( 1 ) Y 4 ( 1 ) Y 2 ( 3 ) Y 5 ( 4 ) + Y 3 ( 1 ) Y 4 ( 1 ) Y 5 ( 3 ) Y 2 ( 4 )     + Y 4 ( 1 ) Y 5 ( 1 ) Y 2 ( 3 ) Y 3 ( 4 ) − Y 4 ( 1 ) Y 5 ( 1 ) Y 3 ( 3 ) Y 2 ( 4 ) ] ,

b 3 = 2 b 0 [ Y 2 ( 1 ) Y 3 ( 1 ) Y 4 ( 2 ) Y 5 ( 4 ) − Y 2 ( 1 ) Y 3 ( 1 ) Y 5 ( 2 ) Y 4 ( 4 ) + Y 2 ( 1 ) Y 5 ( 1 ) Y 3 ( 2 ) Y 4 ( 4 )     − Y 2 ( 1 ) Y 5 ( 1 ) Y 4 ( 2 ) Y 3 ( 4 ) − Y 3 ( 1 ) Y 4 ( 1 ) Y 2 ( 2 ) Y 5 ( 4 ) + Y 3 ( 1 ) Y 4 ( 1 ) Y 5 ( 2 ) Y 2 ( 4 )     + Y 4 ( 1 ) Y 5 ( 1 ) Y 2 ( 2 ) Y 3 ( 4 ) − Y 4 ( 1 ) Y 5 ( 1 ) Y 3 ( 2 ) Y 2 ( 4 ) ] ,

c = 0.

那么(5)式就降次为

z 4 + b 3 z 3 + b 2 z 2 + b 1 z + c = 0. (12)

因为 c = 0 ，且 z = e ξ > 0 ，所以(12)式就变为

z 3 + b 3 z 2 + b 2 z + b 1 = 0. (13)

若 z 1 、 z 2 、 z 3 、 z 4 是方程(12)的4个根，那么 ln z 1 、 ln z 2 、 ln z 3 、 ln z 4 就是方程(5)的4个根， − ( ln z 1 + ln z 2 + ln z 3 + ln z 4 ) 是第5个根。

4. 平衡点分析

本节我们采用盛金公式来计算一元三次方程(13)。

令

A = b 3 2 − 3 b 2 , B = b 2 b 3 − 9 b 1 , C = b 2 2 − 3 b 1 b 3 , Δ = B 2 − 4 A C . (14)

下面我们分四类来讨论五次方程的解x。

4.1. 情形①： A = B = 0

令 A = B = 0 ，即

b 3 2 − 3 b 2 = 0. (15)

b 2 b 3 − 9 b 1 = 0. (16)

此时，有三重实根 z 1 = z 2 = z 3 = − b 3 / 3 ，且这个实根要大于零。

在F-u1平面上画出方程(15) (黑色曲线)和(16) (红色曲线)，并画出实根大于零的区域(绿色曲线)，如图1(a)所示。在实根大于零的条件下，可以得到部分黑色曲线和红色曲线满足条件，如图1(b)所示。

Figure 1. The range of z on the F-u1 plane under case ①: (a) No condition z > 0; (b) Have condition z > 0

图1. 情形①下，实根z在F-u1平面上的范围：(a) 不考虑条件z > 0；(b) 考虑条件z > 0

若要满足方程(15)和(16)，就要取图1(b)中黑色曲线和红色曲线的交点。从图1(b)中可以看出，这两条曲线没有交点。所以不存在实根。

所以在情形①下，方程无解。

4.2. 情形②： Δ > 0

令 Δ > 0 ，即

( b 2 b 3 − 9 b 1 ) 2 − 4 ( b 3 2 − 3 b 2 ) ( b 2 2 − 3 b 1 b 3 ) > 0 (17)

Figure 2. Δ = 0 on the F-u1 plane

图2. F-u1平面上Δ = 0

此时，有一个实根 z 1 = − b 3 − ( h 1 1 3 + h 2 1 3 ) 3 和一对共轭虚根 z 2 , 3 = − b 3 + 1 2 ( h 1 1 3 + h 2 1 3 ) ± 3 2 ( h 1 1 3 − h 2 1 3 ) i 3 ，其中 h 1 , 2 = A b 3 + 3 ( − B ± B 2 − 4 A C ) 2 。因为根要大于零，所以去掉共轭虚根，剩下一个实根 z 1 > 0 。

在F-u1平面上画出条件(17) (黑色曲线)，如图2所示。其中画有虚线的区域为 Δ < 0 ，空白区域为 Δ > 0 。这里取空白区域。

因为根要大于零，所以图2中的空白区域被红色曲线分割成图3所示的区域，其中部分区域I、II、III和IV满足条件 z 1 > 0 。

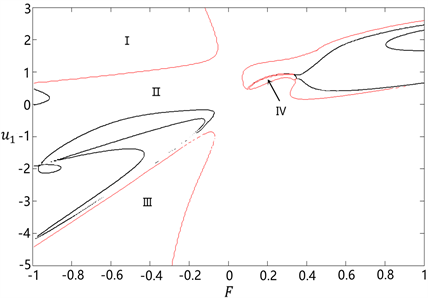
Figure 3. The range of z on the F-u1 plane under case ②

图3. 情形②下，实根z在F-u1平面上的范围

我们分别在图3中的这四个小区域中取值。在区域I中取点 ( − 0.4 , 2 ) ，得到实根 z 1 = 1.0408 ，所以得到解 x 1 = 0.0400 。在区域II中取点 ( − 0.4 , 0 ) ，得到实根 z 1 = 0.1646 ，所以得到解 x 1 = − 1.8040 。在区域III中取点 ( − 0.4 , − 4 ) ，得到实根 z 1 = 0.4087 ，所以得到解 x 1 = − 0.8949 。在区域IV中取点 ( 0.2 , 0.7 ) ，得到实根 z 1 = 0.0222 ，所以得到解 x 1 = − 3.8093 。

所以在情形②下，区域I、II、III和IV都存在一个解，空白区域的其他区域则无解。

4.3. 情形③： Δ = 0

令 Δ = 0 ，即

( b 2 b 3 − 9 b 1 ) 2 − 4 ( b 3 2 − 3 b 2 ) ( b 2 2 − 3 b 1 b 3 ) = 0 (18)

此时，有三个实根，其中一个两重根 z 1 = − b 3 + k ， z 2 = z 3 = − k / 2 ，其中 k = B / A ( A ≠ 0 ) 。因为根要大于零，所以 z 1 , z 2 > 0 。

图2中的黑色曲线满足条件(18)。因为根要大于零，所以在图2中加入满足条件的红色曲线，如图4所示。

接下来我们分析图4中的黑色曲线是否满足条件。图4中的黑色曲线共分为7条，分析可得，黑色曲线I满足 z 2 > 0 ，但 z 1 < 0 ，此时得到一个两重实根 z 2 。黑色曲线II不满足条件，此时无实根。其余5条黑色曲线满足 z 1 > 0 ，但 z 2 < 0 ，此时得到一个实根 z 1 。

所以在情形③下，图4中的黑色曲线II无解，黑色曲线I存在一个两重解，其余5条黑色曲线都存在一个解。

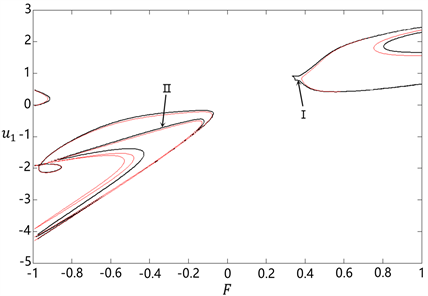
Figure 4. The range of z on the F-u1 plane under case ③

图4. 情形③下，实根z在F-u1平面上的范围

4.4. 情形④： Δ < 0

令 Δ < 0 ，即

( b 2 b 3 − 9 b 1 ) 2 − 4 ( b 3 2 − 3 b 2 ) ( b 2 2 − 3 b 1 b 3 ) < 0 (19)

此时，有三个不等实根 z 1 = − b 3 − 2 A cos cos θ 3 3 ， z 2 , 3 = − b 3 + A ( cos θ 3 ± 3 sin θ 3 ) 3 ，其中 θ = arc cos T ， T = 2 A b 3 − 3 B 2 A 3 ( A > 0 , − 1 < T < 1 ) 。因为根要大于零，所以 z 1 , z 2 , z 3 > 0 。

图2中的虚线区域满足 Δ < 0 。此时，根据条件 z 1 , z 2 , z 3 > 0 ，得到图5所示的虚线区域被红色曲线分割出来的区域，共分割出8个小区域。

Figure 5. The range of z on the F-u1 plane under case ④

图5. 情形④下，实根z在F-u1平面上的范围

在图5的这8个小区域中，我们分析是否满足条件 z 1 , z 2 , z 3 > 0 。分析可得，区域III不满足条件，所以无实根。区域IV和VII都满足条件 z 2 , z 3 > 0 ， z 1 < 0 ，所以都存在两个实根 z 2 , z 3 。此时在这两个区域中取一点 ( − 0.6 , − 2 ) ，得到实根 z 2 = 15.1561 ， z 3 = 0.2316 ，所以得到解 x 2 = 2.7184 ， x 3 = − 1.4626 ，还存在一个解 x 4 = − ( ln z 2 + ln z 3 ) = − 1.2558 。区域I、II、V、VI和VIII都满足条件 z 2 > 0 ， z 1 , z 3 < 0 ，所以都存在一个实根 z 2 。此时在这五个区域中取一点 ( − 0.6 , − 1 ) ，得到实根 z 2 = 0.0732 ，所以得到解 x 2 = − 2.6152 。

所以在情形④下，图5中的区域III无解，区域IV和VII都存在三个解，区域I、II、V、VI和VIII都存在一个解。

4.5. 解个数分析

综上所述，将上述四种情况结合起来，三种颜色的曲线将F-u1平面分割成了16个小区域，共产生了三类解的数量。将相同数量的解的区域合并，得到如下图6所示的解x的个数分布图，共分为9个区域，并存在5条黑色曲线。

Figure 6. Number distribution of x

图6. x的个数分布图

在图6中，可知区域II、IV、V、VI和IX内不存在解，区域I和VIII内存在一个解，区域III和VII内存在三个解。这5条黑色曲线都存在一个解，其中曲线③和④都存在一个两重解。

5. 结论

本文研究了一类5次项和3次项共存的快慢耦合Duffing-van der Pol系统的平衡点问题。求系统的平衡点，得到了关于参数F和u1的一个一元五次方程。这个一元五次方程无法使用求根公式直接求解，先使用一元n次方程的降次解法，将五次方程降到四次。当平衡点方程降到四次时，计算得到常数项的系数为零，所以直接降次为三次方程。再采用盛金公式来对三次方程进行分类求解，得到了四种情形下平衡解在F-u1平面上的分布。综合这四类情形，最终得到了平衡点方程的解在F-u1平面上的分布，如图6所示：区域II、IV、V、VI和IX内不存在解，区域I和VIII内存在一个解，区域III和VII内存在三个解；5条黑色曲线都存在一个解，其中曲线③和④都存在一个两重解。

基金项目

国家自然科学基金项目(11572288)和浙江省自然科学基金项目(LY20A020003)资助。

NOTES

*通讯作者。

参考文献

[1] Xu, Y., et al. (2011) Stochastic Bifurcations in a Bistable Duffing-Van der Pol Oscillator with Colored Noise. Physical Review E, 83, Article ID: 056215.
https://doi.org/10.1103/PhysRevE.83.056215
[2] Li, C., et al. (2013) Response Probability Density Functions of Duffing-Van der Pol Vibro-Impact System under Correlated Gaussian White Noise Excitations. Physics A, 392, 1269-1279.
https://doi.org/10.1016/j.physa.2012.11.053
[3] Zhang, C., et al. (2014) On Two-Parameter Bifurcation Analysis of Switched System Composed of Duffing and van der Pol Oscillators. Communications in Nonlinear Science and Numerical Simulation, 19, 750-757.
https://doi.org/10.1016/j.cnsns.2013.06.028
[4] Zhou, L. and Chen, F. (2014) Chaotic Motions of the Duffing-Van der Pol Oscillator with External and Parametric Excitations. Shock and Vibration, 2014, Article ID: 131637.
https://doi.org/10.1155/2014/131637
[5] Kumar, P., Narayanan, S. and Gupta, S. (2016) Stochastic Bifurcations in a Vibro-Impact Duffing-Van der Pol Oscillator. Nonlinear Dynamics, 85, 439-452.
https://doi.org/10.1007/s11071-016-2697-1
[6] Li, S., Niu, J. and Li, X. (2018) Primary Resonance of Fractional-Order Duffing-van der Pol Oscillator by Harmonic Balance Method. Chinese Physics B, 27, 211-216.
https://doi.org/10.1088/1674-1056/27/12/120502
[7] 高发宝, 王永青. 一类五次非线性系统的全局动力学[J]. 动力系统与控制, 2020, 9(4): 207-213.
[8] 陈乐颀. 一类带有超越功能反应的捕食者-食饵系统的平衡点分析[J]. 内江师范学院学报, 2020, 35(4): 34-37.
[9] 张远达. 浅谈高次方程[M]. 武汉: 湖北教育出版社, 1983.
[10] 林文业. 现代数学与量子力学[M]. 郑州: 郑州大学出版社, 2010.
[11] 秦小兵. 关于高次方程根的研究[J]. 基础教育课程, 2017(10): 65-67.
[12] 姜海馨, 姜玉秋. 论一元高次方程的近似求解[J]. 文存阅刊, 2017(1): 37, 39.
[13] 范盛金. 一元三次方程的新求根公式与新判别法[J]. 海南师范学院学报, 1989(2): 91-98.
[14] 刘延彬, 陈予恕. 余维4的Duffing-Van der Pol方程全局分岔分析[J]. 振动与冲击, 2011, 30(1): 69-72, 110.

为你推荐