1. 引言
设
为n维复空间,
为一个正参数,其中
,让
。
为高斯测度,其中
。
设
是定义在
上的可测函数。若
在
上可积,则这样的全体构成空间
,即
。
Fock空间
。其中
是
中所有整函数构成的集合。特别地,当
时,就是经典的
空间。即
。显然
是
的闭子空间,即
也是希尔伯特空间,它的内积定义为
。
实际上,
是一个再生核希尔伯特空间,其中核函数为
。
当
时,范数
定义为
。
同样的定义
时,范数
被表示为
。
由
的每个线性算子S均可导岀一个
上的函数
,即
。
其中
是S的Berezin变换。因为
是单位向量,所以当S有界时
就有界,并且
。另外,在
上,当
时,
,因此当S是
上的紧算子时,
时,
。
我们主要研究线性算子
上的有界性和紧性。为了说明我们的主要结果,我们需要在
上引入一类酉算子。对于任何
,令
代表示
上由
定义的解析自映射,
表示正规化的再生核,即
。
设
是
上的线性算子
,其中每一个
是
上的单位向量。从变量的变化易知每个
都是
的一个自伴单位算子,参见文献 [1]。同时每个
都将
映射到
,其中
为
的核函数
的有限线性组合构成的集合。
设
是测度空间,
是
上可测函数,并且
;
则
。
是
到自身的有界线性积分算子。进一步,如果
是可分空间,那么T是
上的Hilbert-Schmidt积分算子。
在文献 [2] 中,Wang己经在复平面
上得到了以下结论。
定理A. 如果存在
和
,使得对任意的
都有
,则算子S在
上有界。
定理B. 如果存在
使得当
时都有,则S是
上的紧算子。
定理C. 假设存在
且
,使得对所有的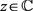 都有
都有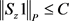 。则S是
。则S是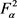 上的紧算子当 且仅当
上的紧算子当 且仅当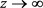 时,
时, 。
。
以上这些结果都是在复平面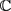 上成立,我们将
上成立,我们将 的这些结果推广到n维复空间
的这些结果推广到n维复空间 上,进一步得到
上,进一步得到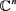 上类似的结果。
上类似的结果。
下面我们介绍本文的主要结果。
定理7. 设S是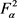 上的线性算子。如果存在常数
上的线性算子。如果存在常数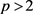 和
和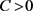 ,使得对于任意的
,使得对于任意的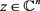 都
都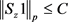 ,
,
则S在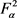 上有界,且有
上有界,且有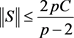 。
。
定理8. 设S是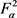 上的线性算子,
上的线性算子,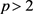 。如果当
。如果当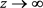 时都有
时都有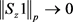 ,则S是
,则S是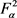 上的算子。
上的算子。
定理9. 设S是 上的线性算子,
上的线性算子,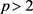 ,若存在正常数C,使得对于任意的
,若存在正常数C,使得对于任意的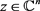 ,都有
,都有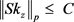 和
和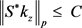 。则S是
。则S是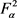 上的Hilbert-Schmidt。特别的,S是紧算子。
上的Hilbert-Schmidt。特别的,S是紧算子。
2. 相关引理
在本节将给岀本文要用到的一系列引理。
在文献 [1] 中,Zhu己经在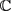 上得到了相应的引理。为了本文定理的证明的需要,我们将此结果推广到
上得到了相应的引理。为了本文定理的证明的需要,我们将此结果推广到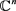 上。得到类似的结果如下:
上。得到类似的结果如下:
引理1. 对于任何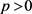 ,对于
,对于 上的任意整函数都有:
上的任意整函数都有:

其中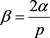 。
。
证明:由范数的定义可得
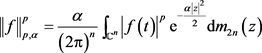 ,
,
令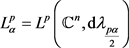 ,则
,则
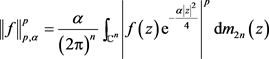 ,
,
当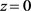 时,可以得到:
时,可以得到:
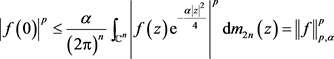 。
。
一般的,对任意的 ,
,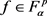 ,我们构造函数
,我们构造函数
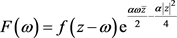 ,
,
则
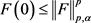 ,
,
即

所以有
 。
。
令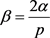 ,显然有
,显然有

所以有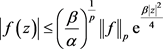 。
。
为了证明,性算子的有界性和紧性,我们先引入下面的引理说明集合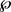 是
是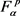 的稠密子空间。
的稠密子空间。
引理2. 设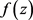 为
为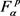 上的核函数的有限线性组合表示的函数,则
上的核函数的有限线性组合表示的函数,则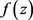 构成的集合表示为
构成的集合表示为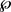 ,其中
,其中

则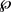 是
是 的稠密子空间,其中
的稠密子空间,其中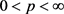 。
。
该引理的证明思想来自文献 [1] 的引理2.11。
证明:当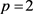 时,结论显然成立。事实上,如果在
时,结论显然成立。事实上,如果在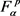 中存在一个函数h,使得对任意的
中存在一个函数h,使得对任意的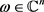 ,h都与
,h都与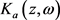 正交,那么
正交,那么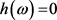 。一般地,由引理1的证明可以知道,可以找到一个正参数
。一般地,由引理1的证明可以知道,可以找到一个正参数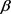 ,使得
,使得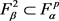 ,且对所有的
,且对所有的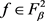 都有
都有 成立。且对任何的
成立。且对任何的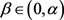 这个结果都成立。如果f是一个多项式,且
这个结果都成立。如果f是一个多项式,且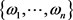 是空间
是空间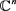 的点,则
的点,则

因为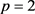 时结论成立,即函数
时结论成立,即函数 在
在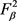 上是稠密的。进一步,在
上是稠密的。进一步,在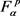 的范数拓扑中,由上式可知每一个多项式都可以由函数
的范数拓扑中,由上式可知每一个多项式都可以由函数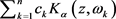 逼近。因此我们可以得到集合
逼近。因此我们可以得到集合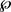 在
在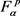 上稠密。
上稠密。
这篇文章中的每一个算子的定义域都包含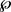 。由于
。由于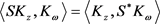 ,则
,则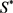 的区域也包含
的区域也包含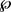 。我们进一步假设函数
。我们进一步假设函数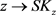 是共轭解析的。
是共轭解析的。
对于任意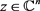 和
和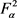 上的任意线性算子S,设
上的任意线性算子S,设 。而每一个
。而每一个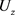 都是
都是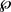 上的自映射。因此当每个S的定义域都包含
上的自映射。因此当每个S的定义域都包含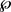 时,
时,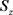 的定义域也包含
的定义域也包含 。
。
为了后面我们证明线性算子的紧性,我们引入下面的引理它给岀算子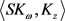 的一个上界。
的一个上界。
引理3. 设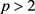 ,S是
,S是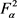 上的线性算子,则对任意的
上的线性算子,则对任意的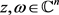 有:
有:

其中 和
和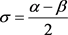 。进一步,如果存在某些正常数C,使得对任意的
。进一步,如果存在某些正常数C,使得对任意的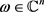 都有
都有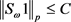 成立,
成立,
则有
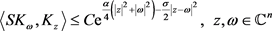 ,
,
证明:由 有
有
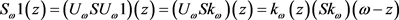 ,
,
在引理1中,对所有的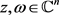 ,有
,有
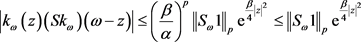 。
。
其中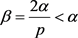 。用
。用 去代替z,则有
去代替z,则有
 ,
,
并对结果进行简化,对任意的 有
有
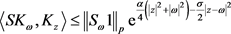 。
。
下面的引理表明对于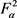 上的每一个线性算子都可以用正则的方式表示积分算子。
上的每一个线性算子都可以用正则的方式表示积分算子。
引理4. 设S是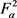 上的线性算子,T是
上的线性算子,T是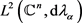 上的积分算子,T定义为:
上的积分算子,T定义为:
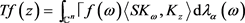 (1)
(1)
S在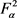 上有界当且仅当T在
上有界当且仅当T在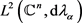 上有界。进一步,当T和S都有界时,则S是T在
上有界。进一步,当T和S都有界时,则S是T在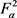 上的一个等价限制。
上的一个等价限制。
证明:任何固定的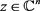 ,函数
,函数
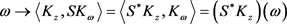 ,
,
是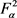 上的整函数。因此,对于任意的
上的整函数。因此,对于任意的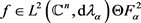 都有
都有 成立,其中
成立,其中 表示
表示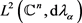 中除去
中除去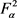 的部分。如果S在
的部分。如果S在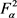 上有界,对于某些
上有界,对于某些 的核函数
的核函数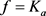 ,通过
,通过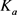 的再生性质有
的再生性质有

由此得岀在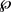 上有
上有 ,对于任意的
,对于任意的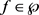 都有
都有 。应用前面的结论,我们得岀了T在
。应用前面的结论,我们得岀了T在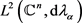 上有界,且S是T在
上有界,且S是T在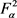 上的等价限制。
上的等价限制。
反之,对于任意的 ,如果T在
,如果T在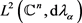 上是有界的,则当
上是有界的,则当 有
有
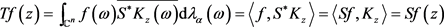 ,
,
这表明T在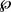 上的限制作用与S是一致的。由于
上的限制作用与S是一致的。由于 在
在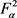 中是稠密的,且T是有界的,所以S是扩展到
中是稠密的,且T是有界的,所以S是扩展到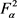 上有界线性算子。
上有界线性算子。
引理5. 对于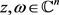 ,有
,有
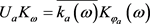 ;
;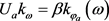 ;
;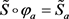 ,
,
其中 是一个依赖于a和
是一个依赖于a和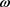 单位模常数。
单位模常数。
证明:

第一个等式证明完毕。
因为
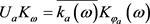 ,
,
由正规化再生核的定义有
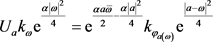 ,
,
化简得
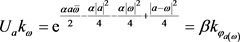 ,
,
其中
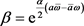 ,
,
第二个式子证明完毕。
通过Berezin变换的定义和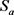 的定义,以及前面己经证明的第二个等式,有
的定义,以及前面己经证明的第二个等式,有

第三个等式证明完成。
引理6. 设S是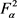 上的线性算子,设常数
上的线性算子,设常数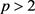 和
和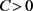 ,使得对所有的
,使得对所有的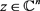 都有
都有 ,则当
,则当 时,
时,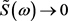 当且仅当对于每一个(或者一些)
当且仅当对于每一个(或者一些)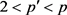 ,有
,有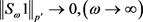 。
。
证明:如果对于某些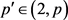 ,有
,有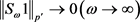 ,应用Hölder’s不等式,当
,应用Hölder’s不等式,当 时,
时,
 ,
,
反之,假设当 时,
时, ,并固定
,并固定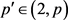 。接下来证明当
。接下来证明当 时,
时,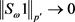 。
。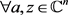 ,我们有
,我们有
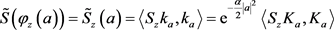 ,
,
其中
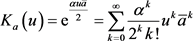 ,
,
将上式带入有
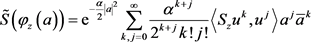 ,
,
对于任意的的正数r,我们考虑积分

其中
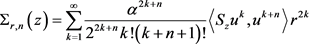 。
。
对于任意的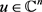 ,当
,当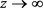 时,有
时,有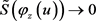 。则对任意
。则对任意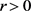 都有
都有
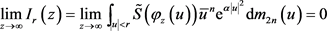 ,
,
进一步,对任意的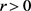 有
有
 ,
,
因此,当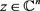 存在一个与z有关的常数C,使得
存在一个与z有关的常数C,使得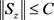 ,对任意的
,对任意的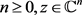 都有
都有

则给定任意的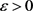 和一个充分小的
和一个充分小的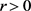 就有
就有
 。
。
进一步得
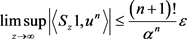 。
。
对任意的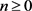 有
有
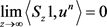 。
。
由于 中的多项式是稠密的,则当
中的多项式是稠密的,则当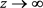 时
时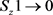 。特别是,对于每一个
。特别是,对于每一个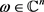 ,当
,当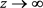 时,
时,
令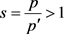 ,存在
,存在 使得
使得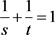 。任意的可测集E有
。任意的可测集E有

由于所有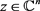 有
有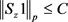 ,这表明
,这表明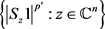 是一致可积的。根据Vitali’s定理有
是一致可积的。根据Vitali’s定理有
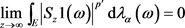 。
。
引理的证明完毕。
3. 主要结果及其证明
定理7. 设S是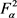 上的线性算子。如果存在常数
上的线性算子。如果存在常数 和
和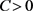 ,使得对于任意的
,使得对于任意的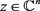 都有
都有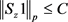 ,
,
则S在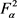 上有界,且有
上有界,且有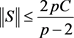 。
。
证明:由引理4,定义的积分算子T在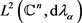 上有界。又由引理3中存在的常数C和
上有界。又由引理3中存在的常数C和
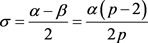 ,对于
,对于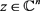 都有
都有

进一步有
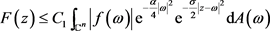 (2)
(2)
其中 和
和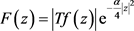 ,对(2)两边平方再应用Hölder不等式
,对(2)两边平方再应用Hölder不等式

其中

再由Fubini’s定理和变量变换可以得到
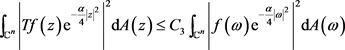 ,
,
其中
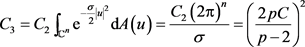 。
。
这表明算子T在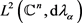 上是有界的,并且
上是有界的,并且
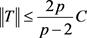 。
。
将T限制在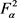 空间上,所以S是有界算子。
空间上,所以S是有界算子。
注记:上面的证明仅取决于引理3中的点态估计给岀的上界,不是关于范数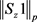 的全部上界的结果。
的全部上界的结果。
下面,我们给岀了 上算子是紧算子的两个充分条件。
上算子是紧算子的两个充分条件。
定理8. 设S是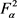 上的线性算子,且
上的线性算子,且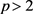 。如果当
。如果当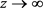 时,都有
时,都有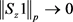 ,则S是
,则S是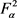 上的紧算子。
上的紧算子。
证明:由假设条件:当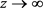 时,都有
时,都有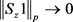 ,则
,则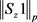 是有界的。由定理7,S在
是有界的。由定理7,S在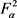 上有界。又由引理4,积分算子T在
上有界。又由引理4,积分算子T在 上是紧算子。
上是紧算子。
则对于任何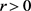 ,定义在
,定义在 上的算子
上的算子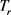 如下:
如下:

其中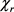 是空间
是空间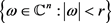 的特征函数。由引理3得到
的特征函数。由引理3得到
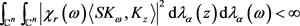 。
。
因此,每个算子 是Hilbert-Schmidt。特别地,每个
是Hilbert-Schmidt。特别地,每个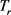 都是空间
都是空间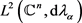 上的紧算子。事实上,令
上的紧算子。事实上,令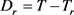 ,则
,则

于是,当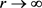 时,有
时,有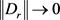 。即T是紧算子。
。即T是紧算子。
给定任何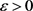 ,选定一个正数R,使得对任意
,选定一个正数R,使得对任意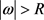 ,都有
,都有 。根据引理3,对任意的
。根据引理3,对任意的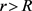 都有
都有
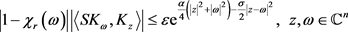 。
。
我们只考虑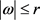 和
和 这两种情况。从定理7的证明可以看岀,给定一个不依赖于
这两种情况。从定理7的证明可以看岀,给定一个不依赖于 和r的正数C,使得对于任意的
和r的正数C,使得对于任意的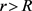 都有
都有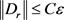 。这表明当
。这表明当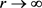 时,有
时,有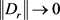 。
。
回顾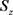 和
和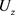 的定义:
的定义:

因为每个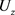 都是
都是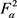 上的单位算子,所以条件
上的单位算子,所以条件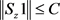 和
和 是等价的。但是,当
是等价的。但是,当 时,
时,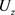 在
在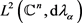 上不一定恒为单位算子。因此,我们很自然地考虑了条件
上不一定恒为单位算子。因此,我们很自然地考虑了条件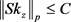 。
。
定理9. 设S是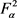 上的线性算子,
上的线性算子,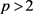 ,若存在正常数C,使得对于任意的
,若存在正常数C,使得对于任意的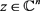 ,都有
,都有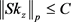 和
和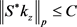 。则S是
。则S是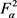 上的Hilbert-Schmidt。特别地,S是紧算子。
上的Hilbert-Schmidt。特别地,S是紧算子。
证明。通过引理1,假设存在一个正常数C,使得
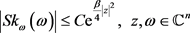 ,
,
其中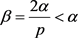 。因为
。因为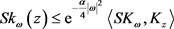 ,进一步有
,进一步有
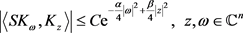 (3)
(3)
因为 ,则对于
,则对于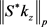 同样有
同样有
 (4)
(4)
将不等式(3)和(4)相乘有

两边开方得
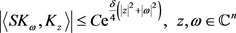 ,
,
其中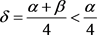 。又因为有
。又因为有
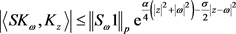 ,
,
因此
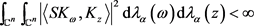 。
。
于是积分算子T,即

是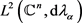 上的Hilbert-Schmidt。因为S是T在
上的Hilbert-Schmidt。因为S是T在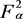 的限制,所以S也是
的限制,所以S也是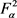 上的Hilbert-Schmidt。
上的Hilbert-Schmidt。
Toeplitz算子的相关应用,在文献 [2] 中己经给岀了复平面C上的结果。在空间 的应用可以 类似得到同样的结果。有关算子的有界性或紧性的更多研究参看文献 [3] - [9]。
的应用可以 类似得到同样的结果。有关算子的有界性或紧性的更多研究参看文献 [3] - [9]。
基金项目
国家自然科学基金(11861024,11561012)。
NOTES
*通讯作者。