基于模糊控制理论的数控加工参数的自适应控制研究

Adaptive Control of CNC Machining Parameters Based on Fuzzy Control Theory

摘要: 针对数控加工参数对整个加工过程的重要性，阐述了一种基于模糊控制理论的数控加工参数自适应控制方法。根据建立的控制模型和模糊控制原理，编写C++源程序，并模拟实验数据进行验证程序的可行性，最后通过VC++可视化软件，将源程序嵌入到现有的数控系统中，实现了加工过程自适应控制的动态显示。结果表明了自适应控制模型的有效性，使数控机床在加工过程中保持良好的稳定性。

Abstract: For the importance of NC machining parameters on the machining process, the adaptive control method of NC machining parameters is elaborated based on fuzzy control theory. According to the established control model and the fuzzy control principle, this paper compiled C++ source procedure, and simulated the experimental data to verify the feasibility of procedures, and finally, embedded the procedures into the existing numerical control system by the VC++ visual software, achieved the dynamic display of adaptive control processing. The results showed the effectiveness of the adaptive control model and made NC machine maintain the good stability in the whole machining process.

1. 引言

数控加工参数的选取直接决定了加工精度和效率，因此产生了越来越多的针对加工参数的优化及建立通用的优化参数数据库的研究。20世纪80年代，在国内有些科研院所研制了一些面向行业的小型数据库，但至今我国还不具有通用性的金属切削知识库系统 [1]。截至目前，最常用的是离线切削参数优化技术，通常以加工效率、加工成本和加工质量中的一个或者多个为目标，建立数学模型，然后选用合适的寻优算法为特定零件的某一道工序选择一组最佳参数，如进给量、主轴转速等 [2]。离线优化技术预测性强，不能反映真实的加工状态，且经查阅文献发现，现有的对数控加工切削参数优化的研究大多是离线优化，只不过运用的优化方法不同而已。因此，为了提高数控系统的加工性能，对加工参数在线优化的研究是迫切需要研究的课题。

2. 基于模糊逻辑的加工参数自适应控制方法

2.1. 模糊控制方案

模糊集合理论是1965年美国伯克莱加州大学教授L.A. Zadeh提出的，它可以将人的判断、思维过程用比较简单的数学形式直接表达出来，从而使对复杂系统做出合乎实际的、符合人类思维方式的处理成为可能。基于模糊集合的模糊逻辑系统为人们解决缺乏精确被控对象模型的控制问题提供了有力的工具 [3]。

对于数控加工过程而言，它是动态的，加工参数时刻发生着变化，很难对加工参数进行精确控制或优化 [4]。因此，利用模糊控制理论正好能解决这一难题，实现加工参数的在线自适应控制。即通过加工过程中随时检测变量来实时调节切削参数，获得最优的切削效率，提高加工质量，使得数控系统能够随环境变化通过自适应调整切削用量实现加工过程的优化 [5]。

对于数控加工参数，普遍认为切削力能够相对反应机床加工状态，并且它也是影响加工性能的最主要参数之一，在加工过程中应尽量保持其平稳，不出现较大波动，因此以切削力为对象开展的研究也最广泛 [6]。但是由于加工环境和监测仪器设备的原因，使得目前很难提取监测力信号进行状态分析 [7]。但实际上，切削力与主电机功率存在以下关系 [8]。

$P=F_{c}v/\left(6\times {10}^4\times \eta \right)$ (1)

式中，P为主电机功率， $F_c$ 为圆周切削力，v为切削速度， $\eta$ 为效率系数。由此可见，当其余参数保持不变时，切削力与机床功率成线性关系，因此选择用主电机电流I代替切削力作为监测信号来进行状态分析。

2.2. 自适应控制模型

由上述，智能数控期望能通过对现场特征物理状态的监测实现数控加工的优化控制，使得在外界条件发生变化时加工系统能做出自适应调整，回归期望状态 [9]。在此，状态监测参数取为主电机电流，根据分析影响切削力的各参数，选择进给速度的变化 $U_{a_f}$ 作为系统调整量，以电流作为决策量构成加工系统的闭环反馈控制 [10]。

根据模糊控制原理，模糊控制模型输入语言变量取为电流偏差 $E_I$ 及偏差变化率 $E{C}_I$，输出语言变量为进给速度变化 $U_{a_f}$，建立基于主电机电流与电压信号监测的数控加工过程进给量自适应调整控制模型如图1所示 [11] [12]。此模糊控制器通过实时调整 $U_{a_f}$ 实现对进给量的自适应调整。

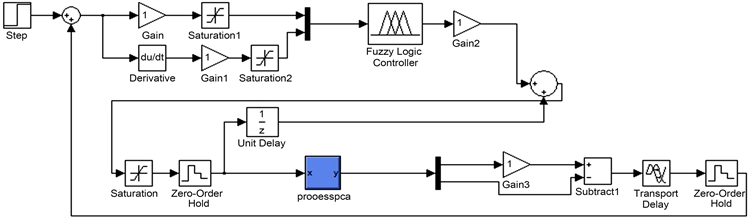
Figure 1. CNC machining adaptive control model based on fuzz theory

图1. 基于模糊逻辑的数控加工自适应控制模型

2.3. 模糊控制算法

根据模糊控制原理，把输入语言变量电流偏差 $E_I$ 及偏差变化率 $E{C}_I$，输出语言变量进给速度变化 $U_{a_f}$ 的模糊集合论域量化档数为3。电流偏差实际取值范围 $E_I=\left[-e,+e\right]$，偏差变化率实际取值范围 $E{C}_I=\left[-\stackrel{\dot{}}{e},\stackrel{\dot{}}{e}\right]$，量化因子 $k_e=k_{ec}=\frac{3}{e}$。为减少计算量，加快响应速度，隶属函数均以三角形函数表示。由

此，根据决策量与被控目标的联系建立49条模糊控制规则。根据给定的输入语言变量论域上的模糊集 $\tilde{E}$ 与 $\widetilde{EC}$，利用推理合成规则得出输出语言变量模糊集 ${\tilde{U}}_{af}=\left(\tilde{E}\times \widetilde{EC}\right)\circ R$，其中R为模糊关系矩阵。

首先，根据建立的49条模糊控制规则，求出每条规则的关系矩阵 $R_i$， $R_i={\left(\tilde{E}\times \widetilde{EC}\right)}^{T_1}\times {\tilde{U}}_{af}$，利用 $R=R_1\vee R_2\vee \cdot \cdot \cdot \vee R_{49}$ 得到模糊关系矩阵R。再利用公式 ${\tilde{U}}_{af}={\left(\tilde{E}\times \widetilde{EC}\right)}^{T_2}\circ R$，设输入 $\tilde{E}=\frac{1}{-6}+\frac{0.5}{-5}$, $\widetilde{EC}=\frac{0.1}{-1}+\frac{0.5}{2}+\frac{1}{4}$，

$R=\left[\begin{array}{ccc}0.5& 0.5& 0.5\\ 0.5& 1& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\end{array}\right]$

则 $\tilde{E}\times \widetilde{EC}\left[\begin{array}{c}1\\ 0.5\end{array}\right]\left[\begin{array}{ccc}0.1& 0.5& 1\end{array}\right]=\left[\begin{array}{ccc}0.1& 0.5& 1\\ 0.1& 0.5& 0.5\end{array}\right]$。再将所得模糊关系矩阵 $\tilde{E}\times \widetilde{EC}$ 写成行向量 ${\left(\tilde{E}\times \widetilde{EC}\right)}^{T_2}=\left[\begin{array}{cccccc}0.1& 0.5& 1& 0.1& 0.5& 0.5\end{array}\right]$ 的形式，则输出语言变量模糊集

${\tilde{U}}_{af}={\left(\tilde{E}\times \left(\tilde{E}\times \widetilde{EC}\right)\right)}^{T_2}\circ R=\left[\begin{array}{cccccc}0.1& 0.5& 1& 0.1& 0.5& 0.5\end{array}\right]\circ \left[\begin{array}{ccc}0.5& 0.5& 0.5\\ 0.5& 1& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\end{array}\right]=\left[\begin{array}{ccc}0.5& 0.5& 0.5\end{array}\right]$

再将其数值具体化，得到被控加工系统的输入调节量

$\Delta a_f=\frac{{\displaystyle \underset{i}{\overset{13}{\sum }}{x}_i{\mu }_{{\tilde{u}}_{a_f}^L}\left(x_i\right)}}{{\displaystyle \underset{i}{\overset{13}{\sum }}{\mu }_{{\tilde{u}}_{a_f}^L}\left(x_i\right)}}$ (2)

式中 $x_i=\left[\begin{array}{ccc}0.5& 0.5& 0.5\end{array}\right]$，输出模糊集合的隶属函数 ${\mu }_{{\tilde{u}}_{a_f}^L}\left(x_i\right)=\left[-3,-2,-1,0,1,2,3\right]$ [13]。

3. 加工参数自适应控制可视化实现

在上述模糊控制算法的基础上，为了方便编程，建立了系统参数运算流程图，如图2所示。根据实验台参数，取电流极限值为18 A，进给速度极限值为1500 mm/min，因此，电流偏差实际取值范围 $E_I=\left[-18,18\right]$，偏差变化率实际取值范围 $E{C}_I=\left[-36,36\right]$，程序运行结果如表1所示。其中，当电流偏差为−18，偏差变化率为−36时，输出进给速度变化值为1500，与模糊规则相符，从实际角度分析，当由于进给速度突然变小致使电流变小时，通过模糊控制，使得输出一个变大的进给速度变化值进行补偿，实现对进给速度的自适应调整，表现为电流的自适应调整，即当系统执行的程序段中进给速度发生变化时，通过自适应控制，使其缓慢变化到既定值，减少突变带来的对机床的冲击，增强系统的稳定性。

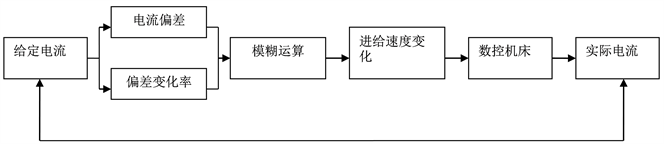
Figure 2. Parameter calculation process

图2. 参数运算流程图

Table 1. Running results

表1. 运行结果

把已经开发的源程序，利用VC可视化编程软件嵌入到已有的TDNC-H8系统，实现参数自适应控制过程的动态显示，以此验证模糊控制器的有效性并显示系统的智能控制功能。由进给速度与电流之间的关系，最终以负载率F = 实际电流/额定电流(%)为显示参数。由于系统的自适应控制过程是动态的，通过截图无法观看其动态效果，只能呈现静态结果。但尽管如此，仍然可以从图3看出，当进给速度F发生突变时，系统负载在模糊控制作用下会逐渐过渡到既定值，这一过程仅需要几秒，但减少了对机床的冲击，实现了平稳的自适应调整和加工过程的优化控制。

Figure 3. Adaptive control process

图3. 自适应控制过程图

4. 结论

数控切削参数的选择是加工过程中的关键要素，它直接影响加工的效率和精度。针对数控加工过程中的不同程序段所设置的参数不同所带来的对系统的影响，采用了模糊控制理论实现加工参数的自适应控制。采用基于电流信号状态监测的模糊自适应控制方法，并建立了数控加工系统的自适应控制模型。同时基于VC的可视化功能实现了加工过程的智能控制动态显示。结果表明建立的模糊自适应控制系统能够以较高的辨识与控制精度达到预期的智能控制要求，减少了由于参数突变带来的对机床的冲击，使得加工较平稳地进行，提高加工稳定性和精度。