基于柔性行动器–评判器的电–热综合能源系统协调优化

Coordinated Optimization of Integrated Electricity-Heat Energy System Based on Soft Actor-Critic

摘要: 电–热综合能源系统的优化调度对于实现系统的能源互补、经济运行具有重要意义。本文提出一种基于柔性行动器–评判器(Soft Actor-Critic, SAC)算法的电–热综合能源系统经济调度方法，首先针对电–热综合能源系统优化调度问题进行建模，然后基于SAC框架将该问题转化为强化学习模型，搭建了强化学习环境。最后对基于SAC的电–热综合能源系统优化运行解结果进行分析，并进一步验证该方法的有效性。

Abstract: The optimal dispatch of integrated electricity-heat energy system (IEHS) is of great significance to the energy complementation and economic operation of the system. An economic dispatch method for IEHS based on the Soft Actor-Critic (SAC) algorithm is proposed in this paper. Firstly, an optimal dispatch model of IEHS is established, and then the problem is transformed into a reinforcement learning model based on the SAC framework, and a reinforcement learning environment is built. Finally, the optimal operation result of integrated electricity-heat energy system based on SAC is analyzed, and the simulations show that the proposed method can effectively solve the problem and reduce the operation cost.

1. 引言

在能源互联网的背景下 [1]，研究电热综合能源系统协调优化问题已成为了多能协调互补运行的一种有效的途径 [2]，有助于进一步提高能源利用率，缓解能源危机，突破传统能源体系结构和行业壁垒。

电–热综合能源系统通过利用热力与电力的互补特性，有利于促进可再生能源消纳，提高能源利用率 [3] [4]。现今对电–热综合能源系统优化问题的求解，主要包括传统非线性方法求解，如非线性求解器IPOPT [5]，智能算法求解，如粒子群算法 [6]，以及线性化简化求解 [7] 三种求解思路。前两种求解思路在电热耦合愈加密切的高维非线性非凸问题求解中，存在求解时间过长，易陷入局部最优解的问题。线性化易于计算和求解，但简化不可避免出现求解调度结果误差较大的问题。

强化学习的自主学习特性适用于决策问题求解。现已有研究将强化学习应用在电力能源系统的经济调度 [8] [9] 和能源管理 [10] [11] 中。经济调度问题中，文献 [10] 基于Q学习提出解决能源系统的优化调度问题的方法，但是对状态和动作的离散处理使得求解过程中存在维数灾难的问题。文献 [8] 采用近端策略优化(proximalpolicy optimization, PPO)算法，其属于在线策略算法，对样本的需求量大，存在采样效率低的问题。文献 [9] 基于深度确定性策略梯度(Deep Deterministic Policy Gradient Algorithm, DDPG)算法求解能源系统优化调度问题，该算法输出确定性策略，在每个状态下仅考虑一个最优动作，易陷入局部最优解。文献 [12] 应用异步优势行动器–评判器(Asynchronous Advantage Actor-Critic, A3C)算法求解能源管理问题，该A3C框架考虑了策略的熵值，但仅将其作为正则项处理。因此，本文采用SAC算法求解电–热综合能源系统优化调度问题，SAC属于随机离线策略算法，将熵最大化添加到优化目标中自主更新，学习探索所有最优策略路径。

本文主要研究基于SAC的电–热综合能源系统协调优化，首先建立电–热综合能源系统优化调度模型，进一步搭建基于SAC框架的电–热综合能源系统优化调度模型，最后通过算例仿真验证该算法求解有效性。

2. 电–热综合能源系统优化调度

2.1. 电–热综合能源系统建模

本文将电–热综合能源系统分电力、热力系统和耦合装置这三部分进行建模研究。

2.1.1. 电力系统

本文以交流潮流作为电力系统的分析方法，电力系统的功率平衡方程表示为：

$\{\begin{array}{l}{P}_i=V_i{\displaystyle \underset{j\in i}{\sum }{V}_j}\left(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij}\right)\\ Q_i=V_i{\displaystyle \underset{j\in i}{\sum }{V}_j}\left(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij}\right)\end{array}\forall i\in {\Gamma }_E^{Node}$ (1)

式中 $P_i$， $Q_i$ 分别为节点i的注入有功、无功功率， $V_i$ 为节点i的电压幅值， $G_{ij}$ 、 $B_{ij}$ 分别为支路ij的电导和电纳， ${\theta }_{ij}$ 为支路ij的相角差。

2.1.2. 热力系统

区域热力系统采用集中供热方式进行供暖，图1表示热力系统简易示意图。

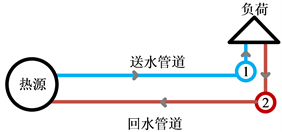
Figure 1. Schematic diagram of heating network

图1. 供热网示意图

热力系统在热源处产生热能，通过送水管道输送到热负荷，经热负荷降温后通过回水管道回流，形成闭合回路。热力系统分为水力模型和热力模型两部分 [13]。

1) 水力模型。热力系统的水力模型表示介质流动，由流量连续性方程，回路压力方程和压头损失方程构成。

$\{\begin{array}{l}A\stackrel{\dot{}}{m}={\stackrel{\dot{}}{m}}_q\\ B{h}_f=0\\ h_f=K\stackrel{\dot{}}{m}\left|\stackrel{\dot{}}{m}\right|\end{array}$ (2)

式中，A为节点–支路关联矩阵，B为回路–支路关联矩阵。 $\stackrel{\dot{}}{m}$ 为管道质量流量速率， ${\stackrel{\dot{}}{m}}_q$ 表示节点注入流量， $h_f$ 表示压头损失，K为管道的阻尼系数。

2) 热力模型。热力模型表示能量传输过程，由节点功率方程，管道温度下降方程和节点介质混合方程构成。

$\{\begin{array}{l}{H}_i=C_p{m}_{q,i}\left(T_{s,i}-T_{o,i}\right)\\ T_{j\left(ij\right)}=\left(T_{i\left(ij\right)}-T_e\right){\text{e}}^{-\frac{\lambda L_{ij}}{C_p{m}_{ij}}}+T_e\\ \left({\displaystyle \underset{k=1}{\overset{n}{\sum }}{m}_{jk}}\right)T_{j\left(jk\right)}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(m_{ij}{T}_{j\left(ij\right)}\right)}\end{array}$ (3)

式中， $H_i$ 为节点i的注入热功率， $C_p$ 为水的比热容， $T_{s,i}$ 、 $T_{o,i}$ 为节点i的送热管道水温和出口水温， $T_{j\left(ij\right)}$ 下标ij表示以i、j为首末端节点的热网管道支路， $T_{i\left(ij\right)}$， $T_{j\left(ij\right)}$ 为该支路的i、j端温度， $T_e$ 表示外界环境温度。

2.1.3. 耦合装置

本文热电联产机组采用抽凝式机组，运行点在多边形区域内，其产电产热功率可用式(4)表示：

$\min \left\{P_{i,\min }^{chp}-{\alpha }_3{H}_{i,t}^{chp},{\alpha }_1+{\alpha }_2{H}_i^{chp}\right\}\le P_{i,t}^{chp}\le P_{i,\max }^{chp}-{\alpha }_3{H}_{i,t}^{chp}\forall i\in {\Gamma }^{chp},t\in T$ (4)

式中， $P_{i,t}^{chp}$， $H_{i,t}^{chp}$ 分别为时段t，第i台抽凝机组电出力和热出力； $P_{i,\max }^{chp}$， $P_{i,\min }^{chp}$ 分别为电出力上下限； ${\alpha }_1$， ${\alpha }_2$， ${\alpha }_3$ 为多边形区域表示系数，在给定热电联产装置下为常数。

2.2. 目标函数

本文以实现电–热综合能源系统的总运行成本最小为目标，同时为实现可在生能源的最大消纳，将可在生能源未消纳的部分作为惩罚项：

$\min F=f_1+f_2+f_3$ (5)

式中， $f_1$ 为常规机组运行成本， $f_2$ 为热电联产装置运行成本， $f_3$ 为弃风惩罚。

1) 常规机组运行成本

$f_1={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left({\displaystyle \underset{i=1}{\overset{N_G}{\sum }}\left(b_0+b_1{P}_{t,i}^G+b_2{\left(P_{t,i}^G\right)}^2\right)}\right)\Delta t}$ (6)

式中， $P_{t,i}^G$ 为常规机组发电功率， $b_0$， $b_1$， $b_2$ 为常规机组能耗系数， $N^G$ 为常规机组的数量。T为调度周期， $\Delta t$ 为调度时间间隔。

2) 热电联产机组运行成本

$f_2={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left({\displaystyle \underset{i=1}{\overset{N_{chp}}{\sum }}\left(a_0+a_1{\left(P_{t,i}^{chp}\right)}^2+a_2{P}_{t,i}^{chp}+a_3{\left(H_{t,i}^{chp}\right)}^2+a_4{H}_{t,i}^{chp}+a_5{P}_{t,i}^{chp}{H}_{t,i}^{chp}\right)}\right)\Delta t}$ (7)

式中， $P_{i,t}^{chp}$， $H_{i,t}^{chp}$ 分别为在时段t，节点i所连热电联产装置发电功率和产热功率； $a_0$， $a_1$， $a_2$， $a_3$， $a_4$， $a_5$ 为热电联产装置能耗系数， $N^{chp}$ 为热电联产的数量。

3) 弃风惩罚

$f_3=k{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\displaystyle \underset{i=1}{\overset{N_w}{\sum }}\left(P_{t,i}^{w,pre}-P_{t,i}^w\right)\Delta t}}$ (8)

式中， $P_{i,t}^w$ 表示在时段t，节点i所连风力发电机出力，k为弃风惩罚系数，为常数。

2.3. 约束条件

1) 节点功率平衡等式约束条件

式(9)、(10)表示网络节点有功功率平衡方程。

$P_{i,t}^G+P_{i,t}^{chp}+P_{i,t}^w-P_{i,t}^{load}=P_{i,t}\forall i\in {\Gamma }_E^{Node},t\in T$ (9)

$H_{i,t}^{chp}-H_{i,t}^{load}=H_{i,t}\forall i\in {\Gamma }_H^{Node},t\in T$ (10)

式中， ${\Gamma }_E^{Node}$ 、 ${\Gamma }_H^{Node}$ 为电力系统、热力系统节点集合，T为调度时段。 $P_{i,t}^{load}$ 、 $H_{i,t}^{load}$ 分别为时段t，节点i的电负荷和热负荷功率。

2) 网络安全约束

为实现电–热综合能源系统安全可靠运行，系统应满足式(11)~式(13)的网络约束。

$V_{i,\min }\le V_i\le V_{i,\max }\forall i\in {\Gamma }_E^{Node}$ (11)

$T_{s_{j,\min }}\le T_{s_j}\le T_{s_{j,\max }}\forall i\in {\Gamma }_H^{Node}$ (12)

$m_{k,\min }\le m_k\le m_{k,\max }\forall k\in {\Gamma }_H^{pipe}$ (13)

式中： $V_{i,\max }$， $V_{i,\min }$ 分别为节点i电压幅值的上限和下限； $T_{sj}$ 为流入热网节点j的热水温度， $T_{s_{j,\max }}$， $T_{s_{j,\min }}$ 为供水温度上、下限； $m_{jk}$ 为热水管道k的质量流量速率， $m_{k,\max }$， $m_{k,\min }$ 分别为其上、下限。

4) 热电联产装置约束

热电联产机组应满足爬坡约束：

$-ram{p}_{down}^{chp}\le P_{i,t}^{chp}-P_{i,t-1}^{chp}\le ram{p}_{up}^{chp}\forall i\in {\Gamma }^{chp},t\in T$ (14)

式中： $P_{i,t}^{chp}$， $P_{i,t-1}^{chp}$ 分别为前后两个时段的热电联产发电功率， $ram{p}_{up}^{chp}$， $ram{p}_{down}^{chp}$ 分别为热电联产装置爬坡速率上下限。

5) 可再生能源约束

$0\le P_{i,t}^w\le P_{\max }^w\forall i\in {\Gamma }^w,t\in T$ (15)

式中， $P_{i,t}^w$ 表示时段t，风机i发电功率， $P_{\max }^w$ 为其最大出力值。

6) 常规机组出力约束

$P_{i,\min }^G\le P_i^G\le P_{i,\max }^G\forall i\in {\Gamma }_E^G$ (16)

同时满足爬坡约束：

$-ram{p}_{down}^G\le P_{i,t}^G-P_{i,t-1}^G\le ram{p}_{up}^G\forall i\in {\Gamma }^G,t\in T$ (17)

式中： $P_{i,\max }^G$， $P_{i,\min }^G$ 分别为机组出力上、下限， $ram{p}_{up}^G$， $ram{p}_{down}^G$ 分为为机组爬坡速率上、下限。

3. 基于SAC的电–热耦合综合能源系统优化调度模型

标准强化学习自主训练以实现长期奖励最大化，SAC在标准的强化学习优化目标基础上扩充了最大熵目标，最优策略还旨在最大化各个观测状态下的信息熵 [14]：

$J\left(\pi \right)={\displaystyle \underset{t=0}{\overset{T}{\sum }}{E}_{\left(s_t,a_t\right)\sim {\rho }_{\pi }}\left[r\left(s_t,a_t\right)+{\alpha }_t{\rm H}\left(\pi \left(\cdot |s_t\right)\right)\right]}$ (18)

其中 ${\rm H}\left(\pi \left(\cdot |s_t\right)\right)$ 为信息熵项， ${\alpha }_t$ 为温度系数。

在优化目标中增加最大熵鼓励探索过程，提升学习速度。温度系数采用最小化式(19)进行自动调整：

$J\left({\alpha }_t\right)=E_{a_t\sim {\pi }_t}\left[-{\alpha }_t\log {\pi }_t\left(a_t|s_t;a_t\right)-{\alpha }_t{\rm H}\right]$ (19)

SAC是基于Actor-Critic框架的深度强化学习算法，由策略网络和价值网络构成，其中价值网络用两个结构相同的神经网络近似软Q值，训练软Q函数参数以最小化软贝尔曼残差：

$J_Q\left(\theta \right)=E_{\left(s_t,a_t\right)\sim D}\left[\frac{1}{2}{\left(Q_{\theta }\left(s_t,a_t\right)-\left(r\left(s_t,a_t\right)+\gamma E_{s_{t+1}\sim p}\left[V_{\bar{\theta }}\left(s_{t+1}\right)\right]\right)\right)}^2\right]$ (20)

并通过独立梯度去优化两个网络：

${\hat{\nabla }}_{\theta }{J}_Q\left(\theta \right)={\nabla }_{\theta }{Q}_{\theta }\left(s_t,a_t\right)\cdot \left(Q_{\theta }\left(s_t,a_t\right)-\left(r\left(s_t,a_t\right)+\gamma \left(Q_{\bar{\theta }}\left(s_{t+1},a_{t+1}\right)-\alpha \log \left({\pi }_{\varphi }\left(a_{t+1}|s_{t+1}\right)\right)\right)\right)\right)$ (21)

策略网络输出为高斯分布的均值和标准差，在进行策略网络的参数更新时，使用Q值更小的网络来作为critic网络减少偏差。参数更新近似梯度为：

${\hat{\nabla }}_{\varphi }{J}_{\pi }\left(\varphi \right)={\nabla }_{\varphi }\alpha \log \left({\pi }_{\varphi }\left(a_t|s_t\right)\right)+\left({\nabla }_{a_t}\alpha \log \left({\pi }_{\varphi }\left(a_t|s_t\right)\right)-{\nabla }_{a_t}Q\left(s_t,a_t\right)\right){\nabla }_{\varphi }{f}_{\varphi }\left({\epsilon }_t;s_t\right)$ (22)

根据强化学习环境，状态，动作，奖励这4个基本要素，结合电-热综合能源系统调度模型建立基于SAC框架的优化调度模型。

1) 动作空间。将所研究系统的控制变量常规机组发电功率，热电联产发电功率以及热电联产热功率作为动作变量，如下所示。

$A=\left\{P_i^G,H_i^{chp},P_i^{chp}\right\}$ (23)

2) 状态空间。所研究系统的状态变量电负荷，风力发电功率，热电联产装置发电功率，常规机组出力，热负荷，热电联产装置产热功率以及环境温度构成状态空间：

$S_E=\left\{P_i^G,P^{load},P^w,P_i^{chp},H^{load},H_i^{chp},T_e\right\}$ (24)

3) 环境。以文献 [12] 为基础搭建强化学习环境，通过策略网络得到当前动作作用于环境，得到即时奖励和下一时段的状态，起到状态转移的作用，并为策略评估提供奖励值。

4) 奖励函数。强化学习目标为实现长期奖励最大化，则将优化目标的相反数设计为即时奖励，同时根据约束条件设置惩罚机制加入到即时奖励中得到最终的奖励函数。惩罚项统一表达形式为式(25)

${\varphi }_v={\beta }_v\cdot \left[\left(v-v_{\max }\right)f\left(v_{\max }-v\right)+\left(v_{\min }-v\right)f\left(v-v_{\min }\right)\right]$ (25)

$f\left(x\right)=\{\begin{array}{c}0x\ge 0\\ 1x<0\end{array}$ (26)

式中， ${\beta }_v$ 为惩罚系数，根据不同的越限惩罚设置相应的常数系数。以常规机组出力越限惩罚式(16)为例，设置惩罚项式(27)，为使训练过程中机组出力不越限，设置较大的正惩罚系数值，当机组出力越限时，将引入惩罚，造成奖励函数值大幅降低。约束条件(11)~(17)处理过程类似，不再赘述。

${\varphi }_{P_G}={\beta }_{P_G}\cdot \left[\left(P_i^G-P_{i,\max }^G\right)f\left(P_{i,\max }^G-P_i^G\right)+\left(P_{i,\min }^G-P_i^G\right)f\left(P_i^G-P_{i,\min }^G\right)\right]$ (27)

奖励函数包括常规机组运行成本，弃风惩罚，热电联产装置运行成本以及变量越限惩罚。

$r_t=-\left(f_1+f_2+f_3+{\varphi }_{P^G}+{\varphi }_{P^{G_t-G_{t-1}}}+{\varphi }_V+{\varphi }_{P^{chp}}+{\varphi }_{P^{ch{p}_t-ch{p}_{t-1}}}+{\varphi }_T+{\varphi }_m\right)$ (28)

式中 $f_1$ 、 $f_2$ 、 $f_3$ 分别为电力系统、热力系统运行成本以及弃风惩罚。 ${\varphi }_{P^G}$， ${\varphi }_{P^{G_t-G_{t-1}}}$ 分别为常规机组出力越限及爬坡越限惩罚项， ${\varphi }_V$ 为系统节点电压越限惩罚。 ${\varphi }_{P^{chp}}$ 、 ${\varphi }_{P^{ch{p}_t-ch{p}_{t-1}}}$ 为热电联产机组出力及爬坡越限惩罚项， ${\varphi }_T$ 为系统节点温度越限惩罚， ${\varphi }_m$ 为系统管道质量流量速率越限惩罚。

4. 算例分析

本文采用如图2所示电–热综合能源系统进行算例分析 [15]。电力系统中G1，G2为两台常规发电机组，W1为风电场，CHP1，CHP2为两台热电联产机组。

SAC策略神经网络和价值神经网络均包括两层隐藏层，结构示意图如图3和图4所示，神经元数目为256，策略网络激活函数设置为线性整流函数，反向传播学习率为0.0003，价值网络激活函数设置为带泄露线性整流函数，学习率为0.0003，温度系数初值为0.01，自更新学习率设置为0.0001，对于上述网络系数更新算法均采用交替乘子法。经验回放单元容量为50000，采样样本量设置为128。

Figure 2. Diagram of integrated electric-thermal energy system

图2. 电–热综合能源系统图

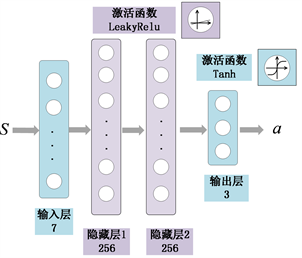
Figure 3. Schematic diagram of the actor network structure

图3. 策略神经网络结构示意图

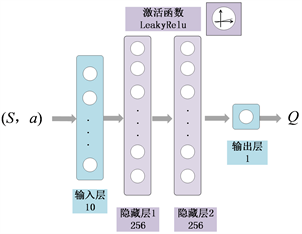
Figure 4. Schematic diagram of the critic network structure

图4. 价值神经网络结构示意图

1) 奖励函数曲线

针对上述算例模型，采用SAC算法进行自学习训练，最终得到的奖励函数曲线及与DDPG算法对比如图5所示，有无熵正则情况下的对比如图6所示：

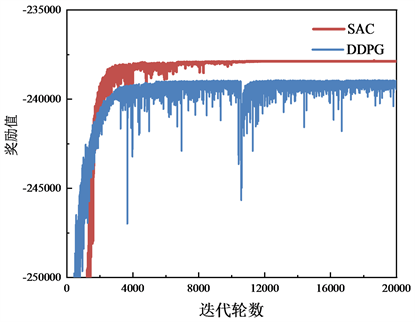
Figure 5. Comparison between SAC and DDPG

图5. SAC与DDPG算法对比

Figure 6. Comparison of the entropy item

图6. 有无熵正则项对比

从图中可以看出，经过10,000轮训练之后奖励曲线收敛，和采用确定性策略梯度算法以及去掉熵正则项得到的计算结果相比，SAC更快达到收敛，并且收敛到较大的奖励值。这是由于SAC将最大信息熵加入到目标函数中，当对动作进行采样时，概率较小的动作可能能够获得更大的Q值，从而鼓励智能体对动作空间进行探索，从不同的方式探索各种最优的可能性，面对干扰时能够更容易做出调整，具有更强的探索能力，能够避免过快陷入局部最优解的困境。同时，与DDPG算法相比较，SAC训练过程稳定性更高，DDPG算法收敛过程存在较大波动，导致训练过程中部分结果超出可行域范围，使得奖励值大幅降低，而SAC收敛过程中无明显波动。

2) 调度结果分析

在网络训练完成之后，可利用策略网络进行调度控制策略的生成。本文采用SAC计算得到的电-热综合能源系统调度结果如图7、图8所示，

Figure 7. Power system output results

图7. 电力系统出力结果

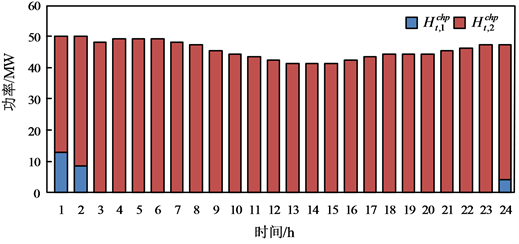
Figure 8. Heating system output results

图8. 热力系统出力结果

图7表示各个机组发电量，可以看到，在负荷需求较小的时段内，如图中时刻1，两台成本较高的发电机均以最小出力运行。在常规机组满足最小出力的情况下，负荷需求主要由成本较小的热电联产装置和风力发电机组承担。由于弃风成本的存在，风电始终满足最大消纳；热电联产装置发电成本较常规机组低，因此往往会承担更多负荷，但因为热电联产机组同时进行电能和热能的供应，其发电出力也在一定程度上受到热负荷的限制。白天时段内随着用电负荷上升和风电出力的降低，成本较低的常规机组2优先增加出力。从图8中可以看出，在热负荷的供应过程中，热力系统优先提高成本较低的热电联产机组2的出力。从图7及图8的计算结果可以看出，SAC算法能够针对电–热综合能源系统优化问题给出正确的调度结果。

3) 对比分析

为进一步验证本文SAC算法的有效性，并验证本文所提方法相较于传统方法的优越性，将本文基于SAC的电–热综合能源系统优化算法、粒子群算法(PSO)以及DDPG算法应用于前述算例，对该电-热综合能源系统进行优化求解，并将优化后的运行成本进行比较，如表1所示。

从优化结果可以看出，SAC算法具备最好的寻优能力，采用SAC算法的得到调度成本最优，小于采用PSO方法得到的计算结果。同时训练好的强化学习模型不需要迭代寻优，只需计算策略神经网络的前向过程。因而其策略神经网络可根据给定的输入，在秒级内给出调度策略，远小于本文测试所用的粒子群算法的296 s计算时间，满足实际工程应用的需求。与DDPG算法相比则可以看出，在引入最大熵等改进措施之后，SAC算法具有更好的探索能力，不易收敛到局部最优解，因此SAC算法得到的计算结果优于采用DDPG算法得到的计算结果。综上所述，本文所提出基于SAC的电热综合能源系统优化调度方法计算性能优于传统算法。

Table 1. Results of different algorithms

表1. 不同算法优化结果对比

5. 结论

本文提出了一种基于SAC算法的电–热综合能源系统经济调度方法，该算法采用连续控制策略，避免了离散化带来的高维求解困难问题，同时将最大熵添加到优化目标中，探索各种最优可能性。将本文所提算法与粒子群算法进行对比，验证了本文所提方法的有效性，另外也对两种深度强化学习学习奖励曲线和损失函数曲线进行对比，表明SAC算法在解决电–热综合能源系统的优化调度问题中探索能力更强，收敛稳定性更好，更适用于电–热综合能源系统的经济调度问题。

基金项目

电力物联网关键技术(2020YFB0905900)。