1. 引言
机械零件在机械动力工程引起的振动能量分布与传递一直以来是研究人员研究的方向之一。在实际结构振动中,多以零件的应力应变作为衡量振动大小的依据,缺少能量的概念。有限元功率流法就是基于结构的能量分析振动的特性。
三维轴承座结构广泛存在于机械工程结构中。轴承基座不仅为轴提供支撑,还承受轴传递的各向载荷。可靠的轴承座对于在减小轴在运转过程中的振动及保证机械设备能够正常作业方面具起到很重要的作用。利用有限元功率流方法对轴承座的振动能量流动的强度和方向进行分具有重要的理论意义和实用价值。
基于功率流研究的对象大都是梁、板等结构。Noiseux等 [1] 首次提出了功率流的概念,将声强作为功率流的概念引入到梁和平板的振动中。Gavric和Pavic [2] 首次基于有限元的思想,对梁、平板以及壳体结构中的功率流进行了分析,并且给出了结构声强(功率流密度)公式。Abbiati等 [3] 进行了基于分段时间积分和状态空间建模的混合仿真计算框架研究。Wong等 [4] 研究了损伤板的结构功率流,分析了降低刚度和板上存在小圆孔的两种情况下功率流能量的变化。Xu等 [5] 对有孔和无孔复合板进行研究,发现圆孔会影响板中振动能量的传递大小和路径,同时发现最大能量处并非对应的是最大应力处。Li等 [6] 采用可视化技术,观察了耦合板的能量流动,得到了不同激励下耦合板的能量大小和传递路径。游进等 [7] 在L型板上加入了两个不相关的白噪声激励,得到板在白噪声激励作用下的能量响应和功率流。李凯等 [8] 基于结构声强法研究了加筋板的振动能量传输,并且分析了不同阻尼器能量耗散特性。乔志等 [9] 比较了有限元功率流法和导纳功率流法的结果,发现两者的结果十分吻合,同时证明基于有限元功率流方法的正确性。朱翔等 [10] 利用1/4点单元法模拟了裂纹,并且得到了裂纹结构在不同裂纹参数下的声强矢量图和流线图。
在瞬态功率流研究中,文献 [11] 研究了简支板结构在受到钢球冲击时的瞬态功率流,得到了板的能量流线图。文献 [12] 利用功率流方法分析了人体头骨在受到撞击时的能量分布,以此来确定头部在受到外部撞击时的严重受损部位。文献 [13] 研究了在瞬态冲击下的钢板功率流,并且提出了能量波的概念。
在众多学者的研究中较少文献对三维实体的功率流进行研究。本文以轴承座为研究对象,分析在受到简谐力作用下裂纹对轴承座的振动影响。实现了载荷冲击下裂纹轴承座的能量分布和传递的可视化研究。
2. 理论基础
2.1. 功率流理论
功率流是一个与时间有关的向量,代表结构的瞬时能量,单位面积上的功率流也称作结构声强。Pavic [2] 利用有限元方法提出了功率流的计算方法,并给出了表达式:
(1)
式(1)中
和
为t时刻和l方向的应力分量和速度分量。
对于一维梁单元,功率流的结构表达式为:
(2)
对于二维板壳单元,单元的位移及力如图1所示。功率流表达式为:
(3)
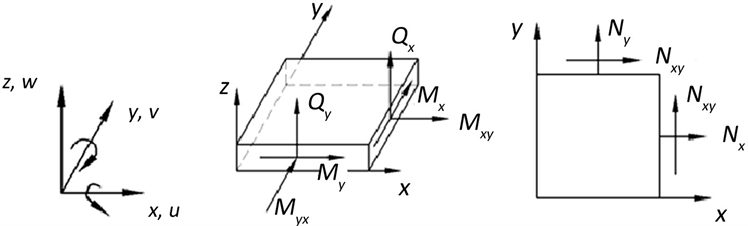
Figure 1. Displacement and internal forces of plate and shell elements
图1. 板壳单元横截面位移及内力
式(2)和(3)中
和
分别为x和y方向的面内轴向力;
和
分别为x和y方向的面内剪力;
、
和
分别为x、y和z方向的横向剪力;
为扭转力;
、
和
分别为x、y和z方向的弯矩;
和
为扭矩;
、
和
分别为三个方向的位移共轭复数;
、
和
分别为x、y和z方向的转角共轭复数;
对于三维实体单元,取六面体微体为研究对象,如图2所示。功率流表达式为:
(4)
式(4)中
为法线n方向上的正应力;
为1方向和2方向上的剪应力;
分别为法线x、y和z方向上的复位移的共轭。
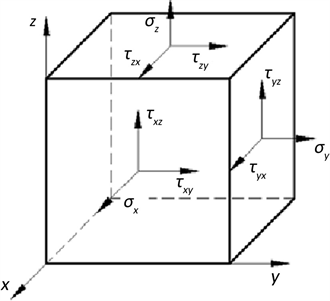
Figure 2. Displacement and internal forces of soild elements
图2. 实体单元应力及位移
2.2. 矢量可视化技术
随着计算机系统的应用越来越广泛,导致了大量数据的产生,对于数据的分析超出了人们的处理能力。因此有了可视化技术的发展。一般意义的可视化定义为:可视化是一种使复杂信息能够容易和快速被人理解的手段,是一种聚焦在信息重要特征的信息压缩语言,是可以放大人类感知的图形化表示方法。可视化就是把数据、信息和知识转化为可视的表示形式并获得对数据更深层次的认识的过程 [14] [15]。
矢量场在科学计算和工程分析中扮演着非常重要的角色,矢量场数据可视化一般都至少要包括三个主要步骤:矢量数据的预处理、矢量数据的映射以及矢量场的绘制和显示。
3. 轴承座功率流分析
3.1. 轴承座模型
轴承基座为左右对称的实体结构,是转轴和台面之间的连接部件之一,在其内部可以安装轴承,并起到轴承的固定作用。轴承基座的三维主视图和俯视图如图3和图4所示。轴承座采用普通碳钢Q235,弹性模量为2.1 × 1011 Pa,泊松比为0.3。为了使计算及划分网格方便,在使用有限元软件建立模型时去掉了轴承座上的凸台及圆孔部分,单元类型为C3D8R,模型的边界条件为底部固定约束。在轴承座与轴承接触部位上施加两个简谐压力载荷。
3.2. 轴承座振动功率流分析
首先利用有限元功率流研究无裂纹轴承座的能量发布及传递特性。对轴承座施加简谐力,简谐力的频率范围为1~100 Hz。选取简谐力频率为50 Hz的工况进行分析,获得轴承座的应力云图、功率流云图和功率流矢量图。图5为轴承座受到激励后的应力云图,图6为轴承座在此工况下的功率流云图,图7和图8分别为此激励下的功率流矢量图和功率流矢量等长图。可视化图形的颜色表示能量的区别,故这些图的应力或功率流的大小通过颜色来显示,其中红色代表值最大,也说明了此处的应力集中或能量聚集。
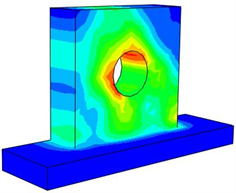 (a) 轴侧图
(a) 轴侧图 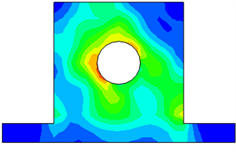 (b) 正视图
(b) 正视图
Figure 5. Stress nephogram of bearing block under harmonic excitation
图5. 轴承座在简谐激励下的应力云图
 (a) 轴侧图
(a) 轴侧图 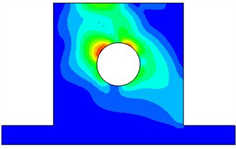 (b) 正视图
(b) 正视图
Figure 6. Power flow of bearing block under harmonic excitation
图6. 轴承座在简谐激励下的功率流云图
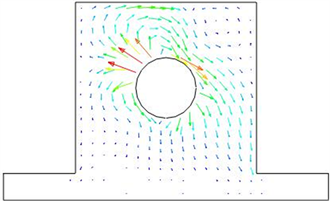
Figure 7. Power flow of bearing block under harmonic excitation
图7. 轴承座在简谐激励下的功率流矢量图
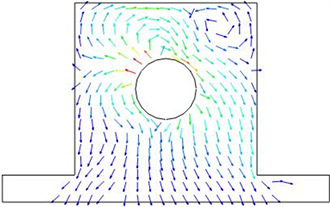
Figure 8. Isometric power flow of bearing block under harmonic excitation
图8. 轴承座在简谐激励下的功率流矢量等长图
图6~8给出了几种不同的功率流表达形式,这几种形式分别为功率流云图、功率流矢量图和功率流矢量等长图。功率流云图表现轴承座内部能量的分布状态;功率流矢量图表达的是能量的传递路径及大小,通过矢量图可以预测能量下一时刻的流动方向,但是由于有些部位的功率流值比较小,所以导致矢量较短,表现的结果并不是很清晰,无法判断矢量的方向。由此便产生了功率流矢量等长图,把所有的矢量长度都设为一致,即假设每个矢量的大小都相等,这样就可通过矢量等长图确定能量的流动方向。
对比图5和图6可以看出在受到简谐力的作用时,应力主要集中在轴承座与轴承接触面的右上方和左下方。但是功率流云图却显示能量集中在轴承座与轴承接触面的左上方和右上方,因此可以得出,应力集中区域并不是能量集中区域。能量包含的不仅是应力信息还有应变的信息,当应力最大时应变并不一定也是最大。因此产生了能量集中区域和应力集中区域的差异。由功率流矢量等长图可以看出能量的流动方向,即能量最终全部流向了轴承座上方和轴承座底部。
3.3. 含裂纹的轴承座功率流分析
轴承座在长期的振动下可能会产生裂纹,裂纹的产生将会影响结构的刚度,进一步影响结构的固有频率等其他特性。有限元功率流可以用来分析裂纹轴承座的应力和能量分布,获得裂纹对轴承座结构的影响,从而为结构设计及安全运行提供依据。
裂纹轴承座的尺寸模型与无裂纹时一样,不同地方是在轴承座的下方加了一个40 mm长的横向裂纹。图9、图10、图11和图12分别为在简谐力频率为50 Hz激励下裂纹轴承座的应力分布云图、功率流云图、功率流矢量图和功率流矢量等长图。
 (a) 轴测图
(a) 轴测图 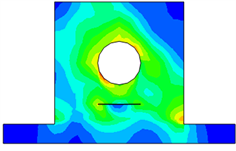 (b) 正视图
(b) 正视图
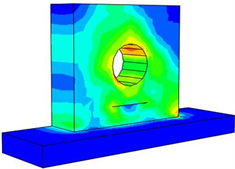
Figure 9. Stress nephogram of bearing block with a crack under harmonic excitation
图9. 裂纹轴承座在简谐激励下的应力云图
 (a) 轴测图
(a) 轴测图 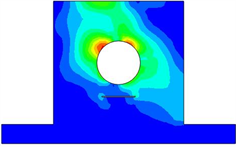 (b) 正视图
(b) 正视图
Figure 10. Energy flow nephogram of bearing block with a crack under harmonic excitation
图10. 裂纹轴承座在简谐激励下的功率流云图
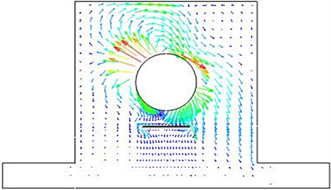
Figure 11. Energy flow of bearing block with a crack under harmonic excitation
图11. 裂纹轴承座在简谐激励下的功率流矢量图
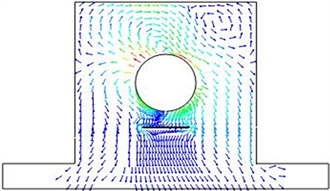
Figure 12. Isometric energy flow of bearing block with a crack under harmonic excitation
图12. 裂纹轴承座在简谐激励下的功率流矢量等长图
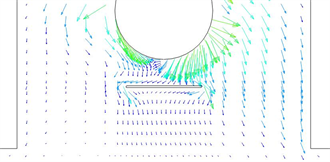
Figure 13. Partial enlargement of crack vector
图13. 裂纹矢量局部放大图
对比图5和图9的应力云图可以发现当含有裂纹时,在裂纹两端应力存在集中现象,并且在裂纹的底部没有应力分布,即裂纹阻挡了应力的传递。对比图6和图10可以得出含有裂纹的轴承座能量集中部位依然是左上方和右上方部位,但是通过功率流云图可以发现在裂纹两端存在能量集中现象,这一点与应力分析结果是吻合的。可以看出裂纹对能量的传递是有一定影响的,由于裂纹处的矢量长度较短表达不清晰,为了更清楚的从矢量图的角度反映裂纹的影响。图13给出了功率流矢量在裂纹处的局部放大图,图中可以看出矢量在裂纹的两端较长,因此此处的能量较大,在裂纹两端存在能量集中情况。同时根据裂纹边缘的矢量方向可以看出能量是沿着裂纹边缘绕过裂纹流动,在裂纹上端的矢量长度和下端矢量长度相差较大,即能量经过裂纹时耗散了许多,裂纹阻挡了能量的传播。
任何结构的系统都可以看成是质量、刚度与阻尼参数的系统,因此裂纹的存在会影响结构的参数,裂纹将会缩减结构的刚度和增大结构的阻尼,从而使结构的固有频率降低。从功率流的角度分析裂纹对轴承座的影响。即分析有无裂纹的轴承座在相同频率下的总能量大小,图14为含裂纹和不含裂纹的轴承座在0~100 Hz下的自身振动功率大小曲线,由于轴承座的固有频率较高,在0~100 Hz激励下没有发生共振现象,所以随着频率的增加功率流也是逐渐增加的,没有产生极大值现象。图14可以得出在每一频率下含有裂纹的振动能量都比不含裂纹时的振动能量要大。与裂纹缩减了结构的刚度结论是吻合的。因此,从能量的角度分析,当轴承座出现裂纹时自身的能量将发生骤增,这样很不利于轴承座的正常使用。这也为检测轴承座是否出现裂纹提供了一种新的方法。
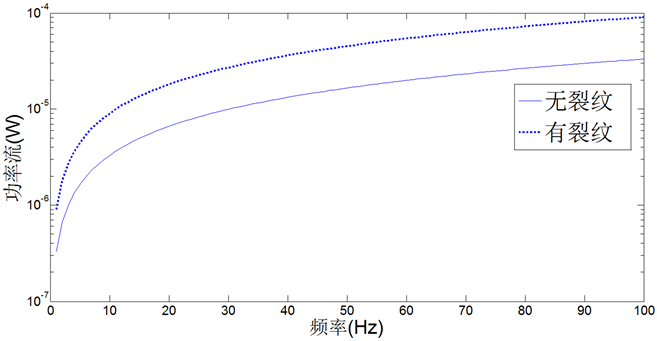
Figure 14. Total power flow of bearing block in steady vibration
图14. 轴承座稳态振动自身总功率流
4. 结论
本文基于有限元功率流法讨论了三维实体轴承座的振动能量传递特性,研究了裂纹对轴承座的能量分布和传递的影响,得到了以下结论:
1) 利用有限元软件可视化了功率流云图和矢量图,得到了三维实体轴承座的稳态振动功率流图,通过功率流云图和矢量图可以清晰的看到当受到外部激励时,轴承座内部的能量大小、分布和传递路径。
2) 利用实体单元细化模拟裂纹,得到了含有裂纹和不含有裂纹的轴承座功率流云图。分析了裂纹对轴承座功率流的影响。发现裂纹会影响功率流的流动方向,当功率流矢量经过裂纹时功率流矢量方向会发生突变,功率流的方向将沿着裂纹边缘流动。同时当能量通过裂纹时会发生耗散,导致裂纹上下部分的能量存在较大差异。
3) 裂纹会加大结构的振动,含有裂纹的振动能量要高于不含有裂纹的振动能量。故有限元功率流研究三维轴承座的能量分布及传递特性为检测轴承座是否出现裂纹提供了一种新的方法。
基金项目
国家自然科学基金资助项目(51675178)。