向量值Hardy空间上的复对称块Toeplitz算子

Complex Symmetric Block Toeplitz Operators on Vector-Valued Hardy Spaces

摘要: 块Toeplitz算子作为数学泛函分析中函数空间上的算子理论研究的重要内容，在物理学、量子力学等方面的模型建立、实际应用有着重要的作用。许多学者在向量值Hardy空间上研究了块Toeplitz算子的核，其正规性、亚正规性以及块复合算子。本文主要研究在向量值Hardy空间中的复对称块Toeplitz算子问题。

Abstract: As an important part of the study of operator theory on function space in mathematical functional analysis, block Toeplitz operator plays an important role in the model building and practical application of physics, quantum mechanics and so on. Many scholars have studied the kernel, normality, hyponormality of block Toeplitz operators and block composition operators on vector-valued Hardy Spaces. In this paper, we study the problem of the complex symmetric block Toeplitz operator on the vector-valued Hardy Space.

1. 引言

2013年Sungeun找到了几类复对称算子的矩阵并研究了其可分解性及应用。特别地，

$T=\left(\begin{array}{cc}A& B\\ 0& C{A}^{*}C\end{array}\right),$

其中C是共轭算子，证明了如果A是复对称的则T可分解的充要条件为A也是可分解的 [1]。

2019年，Dong-O Kang利用 $H^2\left(\mathbb{T}\right)$ 上的共轭算子 $C_{\mu ,\lambda }$，得到结论：Toeplitz算子T关于共轭算子 $C_{\mu ,\lambda }$ 复对称当且仅当T关于共轭算子 $C_{1,\lambda }$ 复对称。借此他构造了一个块Toeplitz算子关于特殊的共轭算子

$C:=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_{1,\lambda }& C_{1,\lambda }\\ C_{1,\lambda }& -C_{1,\lambda }\end{array}\right)$ 复对称的充要条件 [2]。

2. 预备知识

本文中， $B\left(\mathcal{H}\right)$ 表示复可分Hilbert空间 $\mathcal{H}$ 上所有有界线性算子的集合。记 $\mathcal{H}$ 上的恒等算子为I。

定义2.1 若算子 $S:\mathcal{H}\to \mathcal{H}$ 满足对于 $\forall x,y\in \mathcal{H},\forall \alpha \in ℂ$，且满足下列条件：

1) $S\left(x+y\right)=S\left(x\right)+S\left(y\right)$，

2) $S\left(\alpha x\right)=\bar{\alpha }S\left(x\right)$。

则称S为共轭线性算子。

定义2.2 假设 $C:\mathcal{H}\to \mathcal{H}$ 是共轭线性算子，如果满足

1) $C^2=I$，

2) $\langle f,g\rangle =\langle Cg,Cf\rangle$，

其中 $f,g\in \mathcal{H}$。称C为共轭算子。

定义2.3 对于算子 $T\in B\left(\mathcal{H}\right)$，若存在一个共轭算子C使得 $CTC=T^{*}$，则称T为C-对称。如果T是C-对称，那么T也称为复对称。

令 $L_{{ℂ}^n}^2=L^2\left(\mathbb{T}\right)\otimes {ℂ}^n$， $H_{{ℂ}^n}^2=H^2\left(\mathbb{T}\right)\otimes {ℂ}^n$， ${ℂ}^n=\underset{n}{\underset{︸}{ℂ\times ℂ\times \cdots \times ℂ}}$。 $M_n$ 是由所有 $n\times n$ 复矩阵构成的集合。对于矩阵值函数 $\Phi \in L_{M_n}^{\infty }=L^{\infty }\left(\mathbb{T}\right)\otimes M_n$，定义 $T_{\Phi }$ 是向量值Hardy空间 $H_{{ℂ}^n}^2$ 上以 $\Phi$ 为符号的块Toepliz算子，即

$T_{\Phi }h=P_n\left(\Phi h\right),\left(h\in H_{{ℂ}^n}^2\right)$

其中 $P_n$ 是 $L_{{ℂ}^n}^2\to H_{{ℂ}^n}^2$ 上的正交射影。

特别地，如果 $\Phi =\left(\begin{array}{cc}{\phi }_1& {\phi }_2\\ {\phi }_3& {\phi }_4\end{array}\right)$， ${\phi }_j\in L^{\infty }\left(\mathbb{T}\right),j=1,2,3,4$，那么块Toeplitz算子在 $H_{{ℂ}^{\text{2}}}^2$ 有如下表示：

$T_{\Phi }=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\phi }_2}\\ T_{{\phi }_3}& T_{{\phi }_4}\end{array}\right).$

本文引入一个共轭算子 $C_q$ 作为构造共轭算子C的关键，下面对 $C_q$ 的相关内容进行介绍：

定义2.4 [3] 记q为序列 ${\left\{q_m\right\}}_{m=o}^{\infty }$，其中 $q_m\in \mathbb{T}$。令 $C_q:H^2\left(\mathbb{T}\right)\to H^2\left(\mathbb{T}\right)$，即

$C_q\left({\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\hat{f}\left(n\right)z^n}\right)={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\overline{\stackrel{^}{f}\left(n\right)}{q}_n{z}^n}.$

其中 $\hat{f}\left(n\right)$ 是f的傅里叶系数。f的幂级数表示为

$f\left(z\right)={\displaystyle \underset{m=0}{\overset{\infty }{\sum }}{a}_m}{z}^m,{\displaystyle \underset{m=0}{\overset{\infty }{\sum }}{\left|a_m\right|}^2}<\infty \left(a_m=\hat{f}\left(m\right),m=0,1,2,\cdots \right)$

命题2.5 [3] $C_q$ 是 $H^2\left(\mathbb{T}\right)$ 中的共轭算子。

定义2.6 [3] 对于序列 $q={\left\{q_k\right\}}_{k=0}^{\infty }$，若存在 $n\in \mathbb{N}$，使得

$\frac{q_n}{q_0}=\frac{q_{n+k}}{q_k},\forall k\in \mathbb{N}.$

则称这个序列为n度等比序列，且比率为 $\frac{q_n}{q_0}$。所有的等比序列都被称为自然等比序列。

定义2.7 [3] 对于算子 $T\in B\left(\mathcal{H}\right)$，若存在 $\mathcal{H}$ 中一个共轭算子 $C_q$ 使得

$C_{q}T{C}_q=T^{*}.$

则称算子T是 $C_q$ -对称的。

定理2.8 [3] 若Toeplitz算子 $T_f$ 是 $C_q$ -对称的，那么q是一个自然等比序列。换句话说，对于 $\forall k\ge m,m=1,2,\cdots$

$\hat{f}\left(k-m\right)=q_k{\bar{q}}_m\hat{f}\left(m-k\right).$

3. 向量值Hardy空间上的2阶复对称块Toeplitz算子

本部分通过构造2阶复共轭算子来研究2阶复对称块Toeplitz算子。首先我们找出2阶共轭矩阵，考虑下述问题：

若 $A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in M_2$。 $A^2=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$，那么有以下三种情况：

$\begin{array}{l}A=\left(\begin{array}{cc}0& b\\ c& 0\end{array}\right),b^2+c^2=1;\\ A=\left(\begin{array}{cc}a& 0\\ 0& d\end{array}\right),a^2=1,d^2=1,a\ne d;\\ A=\left(\begin{array}{cc}a& b\\ c& -a\end{array}\right),a^2+bc=1.\end{array}$

在文献 [2] 中，作者基于上面的第三种情况，构造了向量值Hardy空间上2阶共轭算子 $C:=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_{1,\lambda }& C_{1,\lambda }\\ C_{1,\lambda }& -C_{1,\lambda }\end{array}\right)$，研究了向量值Hardy空间上的关于C复对称的块Toeplitz算子问题。基于上述论文，本文将进一步研究向量值Hardy空间上关于共轭算子 $C_0:=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q& C_q\\ C_q& -C_q\end{array}\right)$ 复对称的块Toeplitz算子。

在本文中 $C_0$ 一直代表上述共轭算子。

下证 $C_0$ 是共轭算子。由 $C_q$ 是Hardy空间上的共轭算子和上面的讨论，只需证 ${\langle C_{0}f,C_{0}g\rangle }_2={\langle g,f\rangle }_2$， $f={\left(f_1,f_2\right)}^{\text{T}}$， $g={\left(g_1,g_2\right)}^{\text{T}}\in H^2\left(\mathbb{T}\right)\otimes {ℂ}^2$，

$\begin{array}{l}{\langle \frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q& C_q\\ C_q& -C_q\end{array}\right)\left(\begin{array}{c}{f}_1\\ f_2\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q& C_q\\ C_q& -C_q\end{array}\right)\left(\begin{array}{c}{g}_1\\ g_2\end{array}\right)\rangle }_2\\ ={\langle \frac{1}{\sqrt{2}}\left(\begin{array}{c}{C}_q{f}_1+C_q{f}_2\\ C_q{f}_1-C_q{f}_2\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{c}{C}_q{g}_1+C_q{g}_2\\ C_q{g}_1-C_q{g}_2\end{array}\right)\rangle }_2\\ =\frac{1}{2}\langle C_q{f}_1+C_q{f}_2,C_q{g}_1+C_q{g}_2\rangle +\frac{1}{2}\langle C_q{f}_1-C_q{f}_2,C_q{g}_1-C_q{g}_2\rangle \\ =\frac{1}{2}\times 2\langle C_q{f}_1,C_q{g}_1\rangle +\frac{1}{2}\times 2\langle C_q{f}_2,C_q{g}_2\rangle \\ =\langle g_1,f_1\rangle +\langle g_2,f_2\rangle ={\langle \left(\begin{array}{c}{g}_1\\ g_2\end{array}\right),\left(\begin{array}{c}{f}_1\\ f_2\end{array}\right)\rangle }_2.\end{array}$

故 $C_0$ 是共轭算子得证。

还可以验证形如 $\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_{1,\lambda }& C_q\\ C_q& -C_{1,\lambda }\end{array}\right),\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q& C_{1,\lambda }\\ C_{1,\lambda }& -C_q\end{array}\right),\left(\begin{array}{cc}{C}_{1,\lambda }& C_q\\ 0& 0\end{array}\right)$ 的算子不是共轭算子。而 $\left(\begin{array}{cc}{C}_{1,\lambda }& \\ & C_q\end{array}\right)$ 是共轭算子。事实上 $C_{1,\lambda },C_q$ 可以用任意的共轭算子替换仍得共轭算子。

定理3.1 假设 $\Phi =\left(\begin{array}{cc}{\phi }_1& {\phi }_2\\ {\phi }_3& {\phi }_4\end{array}\right)\in L^{\infty }\left(\mathbb{T}\right)\otimes M_2$， $T_{\Phi }=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\phi }_2}\\ T_{{\phi }_3}& T_{{\phi }_4}\end{array}\right)$ 是关于共轭算子 $C_{\text{0}}$ 的复对称算子当且仅当

$\left(\begin{array}{cc}{\hat{\phi }}_1\left(n\right)& {\hat{\phi }}_2\left(n\right)\\ {\hat{\phi }}_3\left(n\right)& {\hat{\phi }}_4\left(n\right)\end{array}\right)=\frac{q_n}{2q_0}\left(\begin{array}{cc}\widehat{\left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)}\left(-n\right)& \widehat{\left({\phi }_1+{\phi }_2-{\phi }_3-{\phi }_4\right)}\left(-n\right)\\ \widehat{\left({\phi }_1-{\phi }_2+{\phi }_3-{\phi }_4\right)}\left(-n\right)& \widehat{\left({\phi }_1-{\phi }_2-{\phi }_3+{\phi }_4\right)}\left(-n\right)\end{array}\right),$

其中 ${\phi }_j\left(z\right)={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}\hat{\phi }}\left(n\right)z^n,z\in \mathbb{T},j=1,2,3,4;n\in \mathbb{Z}$。

证明 因为 $T_{\Phi }$ 是关于 $C_{\text{0}}$ 的复对称算子，所以 $T_{\Phi }{C}_{\text{0}}=C_{\text{0}}{T}_{\Phi }^{*}$。计算可得

$\begin{array}{c}{T}_{\Phi }{C}_{\text{0}}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{T}_{{\phi }_1}{C}_q& T_{{\phi }_2}{C}_q\\ T_{{\phi }_3}{C}_q& T_{{\phi }_4}{C}_q\end{array}\right)\left(\begin{array}{cc}\text{1}& \text{1}\\ \text{1}& -\text{1}\end{array}\right)\\ =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{T}_{{\phi }_1}{C}_q+T_{{\phi }_2}{C}_q& T_{{\phi }_1}{C}_q-T_{{\phi }_2}{C}_q\\ T_{{\phi }_3}{C}_q+T_{{\phi }_4}{C}_q& T_{{\phi }_3}{C}_q-T_{{\phi }_4}{C}_q\end{array}\right)\\ =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\left(T_{{\phi }_1}+T_{{\phi }_2}\right)C_q& \left(T_{{\phi }_1}-T_{{\phi }_2}\right)C_q\\ \left(T_{{\phi }_3}+T_{{\phi }_4}\right)C_q& \left(T_{{\phi }_3}-T_{{\phi }_4}\right)C_q\end{array}\right),\end{array}$

$\begin{array}{c}{C}_{\text{0}}{T}_{\Phi }^{*}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\text{1}& \text{1}\\ \text{1}& -\text{1}\end{array}\right)\left(\begin{array}{cc}{C}_q{T}_{{\phi }_1}^{*}& C_q{T}_{{\phi }_3}^{*}\\ C_q{T}_{{\phi }_2}^{*}& C_q{T}_{{\phi }_4}^{*}\end{array}\right)\\ =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q{T}_{{\phi }_1}^{*}+C_q{T}_{{\phi }_2}^{*}& C_q{T}_{{\phi }_3}^{*}+C_q{T}_{{\phi }_4}^{*}\\ C_q{T}_{{\phi }_1}^{*}-C_q{T}_{{\phi }_2}^{*}& C_q{T}_{{\phi }_3}^{*}-C_q{T}_{{\phi }_4}^{*}\end{array}\right)\\ =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q\left(T_{{\phi }_1}^{*}+T_{{\phi }_2}^{*}\right)& C_q\left(T_{{\phi }_3}^{*}+T_{{\phi }_4}^{*}\right)\\ C_q\left(T_{{\phi }_1}^{*}-T_{{\phi }_2}^{*}\right)& C_q\left(T_{{\phi }_3}^{*}-T_{{\phi }_4}^{*}\right)\end{array}\right).\end{array}$

对比可得

$\{\begin{array}{l}{T}_{{\phi }_1+{\phi }_2}{C}_q=C_q{T}_{{\phi }_1+{\phi }_2}^{*}\\ T_{{\phi }_1-{\phi }_2}{C}_q=C_q{T}_{{\phi }_3+{\phi }_4}^{*}\\ T_{{\phi }_3+{\phi }_4}{C}_q=C_q{T}_{{\phi }_1-{\phi }_2}^{*}\\ T_{{\phi }_3-{\phi }_4}{C}_q=C_q{T}_{{\phi }_3-{\phi }_4}^{*}\end{array}$

由定理2.8可得

$\{\begin{array}{l}\widehat{\left({\phi }_1+{\phi }_2\right)}\left(m-n\right)=q_m{\bar{q}}_n\widehat{\left({\phi }_1+{\phi }_2\right)}\left(n-m\right)\\ \widehat{\left({\phi }_1-{\phi }_2\right)}\left(m-n\right)=q_m{\bar{q}}_n\widehat{\left({\phi }_3+{\phi }_4\right)}\left(n-m\right)\\ \widehat{\left({\phi }_3+{\phi }_4\right)}\left(m-n\right)=q_m{\bar{q}}_n\widehat{\left({\phi }_1-{\phi }_2\right)}\left(n-m\right)\\ \widehat{\left({\phi }_3-{\phi }_4\right)}\left(m-n\right)=q_m{\bar{q}}_n\widehat{\left({\phi }_3-{\phi }_4\right)}\left(n-m\right)\end{array}$

由定义2.6可知 $\frac{q_k}{q_0}=\frac{q_{n+k}}{q_n}$，所以

$\{\begin{array}{l}{q}_0\left[{\hat{\phi }}_1\left(n\right)+{\hat{\phi }}_2\left(n\right)\right]=q_n\left[{\hat{\phi }}_1\left(-n\right)+{\hat{\phi }}_2\left(-n\right)\right]\\ q_0\left[{\hat{\phi }}_1\left(n\right)-{\hat{\phi }}_2\left(n\right)\right]=q_n\left[{\hat{\phi }}_3\left(-n\right)+{\hat{\phi }}_4\left(-n\right)\right]\\ q_0\left[{\hat{\phi }}_3\left(n\right)+{\hat{\phi }}_4\left(n\right)\right]=q_n\left[{\hat{\phi }}_1\left(-n\right)-{\hat{\phi }}_2\left(-n\right)\right]\\ q_0\left[{\hat{\phi }}_3\left(n\right)-{\hat{\phi }}_4\left(n\right)\right]=q_n\left[{\hat{\phi }}_3\left(-n\right)-{\hat{\phi }}_4\left(-n\right)\right]\end{array}$

解得

$\{\begin{array}{l}{\hat{\phi }}_1\left(n\right)=\frac{1}{2}\frac{q_n}{q_0}\left[{\hat{\phi }}_1\left(-n\right)+{\hat{\phi }}_2\left(-n\right)+{\hat{\phi }}_3\left(-n\right)+{\hat{\phi }}_4\left(-n\right)\right]=\frac{1}{2}\frac{q_n}{q_0}{\displaystyle \underset{j=1}{\overset{4}{\sum }}{\hat{\phi }}_j\left(-n\right)}\\ {\hat{\phi }}_2\left(n\right)=\frac{1}{2}\frac{q_n}{q_0}\left[{\hat{\phi }}_1\left(-n\right)+{\hat{\phi }}_2\left(-n\right)-{\hat{\phi }}_3\left(-n\right)-{\hat{\phi }}_4\left(-n\right)\right]=\frac{1}{2}\frac{q_n}{q_0}{\displaystyle \underset{j=1}{\overset{2}{\sum }}\left[{\hat{\phi }}_j\left(-n\right)-{\hat{\phi }}_{j+2}\left(-n\right)\right]}\\ {\hat{\phi }}_3\left(n\right)=\frac{1}{2}\frac{q_n}{q_0}\left[{\hat{\phi }}_1\left(-n\right)-{\hat{\phi }}_2\left(-n\right)+{\hat{\phi }}_3\left(-n\right)-{\hat{\phi }}_4\left(-n\right)\right]=\frac{1}{2}\frac{q_n}{q_0}{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\left(-1\right)}^{j+1}\left[{\hat{\phi }}_j\left(-n\right)+{\hat{\phi }}_{j+2}\left(-n\right)\right]}\\ {\hat{\phi }}_4\left(n\right)=\frac{1}{2}\frac{q_n}{q_0}\left[{\hat{\phi }}_1\left(-n\right)-{\hat{\phi }}_2\left(-n\right)-{\hat{\phi }}_3\left(-n\right)+{\hat{\phi }}_4\left(-n\right)\right]=\frac{1}{2}\frac{q_n}{q_0}{\displaystyle \underset{j=1}{\overset{2}{\sum }}{\left(-1\right)}^{j+1}\left[{\hat{\phi }}_j\left(-n\right)-{\hat{\phi }}_{j+2}\left(-n\right)\right]}\end{array}$

整理得，对 $n\in \mathbb{Z}$，

$\left(\begin{array}{cc}{\hat{\phi }}_1\left(n\right)& {\hat{\phi }}_2\left(n\right)\\ {\hat{\phi }}_3\left(n\right)& {\hat{\phi }}_4\left(n\right)\end{array}\right)=\frac{q_n}{2q_0}\left(\begin{array}{cc}\widehat{\left({\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4\right)}\left(-n\right)& \widehat{\left({\phi }_1+{\phi }_2-{\phi }_3-{\phi }_4\right)}\left(-n\right)\\ \widehat{\left({\phi }_1-{\phi }_2+{\phi }_3-{\phi }_4\right)}\left(-n\right)& \widehat{\left({\phi }_1-{\phi }_2-{\phi }_3+{\phi }_4\right)}\left(-n\right)\end{array}\right).$

注3.2 记

$E_{\text{11}}=\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right),E_{\text{12}}=\left(\begin{array}{cc}1& 1\\ -1& -1\end{array}\right),E_{\text{21}}=\left(\begin{array}{cc}1& -1\\ 1& -1\end{array}\right),E_{\text{22}}=\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right).$

定理3.1^* 假设 $\Phi =\left(\begin{array}{cc}{\phi }_1& {\phi }_2\\ {\phi }_3& {\phi }_4\end{array}\right)\in L^{\infty }\left(\mathbb{T}\right)\otimes M_2$， $T_{\Phi }=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\phi }_2}\\ T_{{\phi }_3}& T_{{\phi }_4}\end{array}\right)$ 是关于共轭算子 $C_{\text{0}}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q& C_q\\ C_q& -C_q\end{array}\right)$ 的复对称算子当且仅当

$\left(\begin{array}{cc}{\hat{\phi }}_1\left(n\right)& {\hat{\phi }}_2\left(n\right)\\ {\hat{\phi }}_3\left(n\right)& {\hat{\phi }}_4\left(n\right)\end{array}\right)=\frac{q_n}{2q_0}\left[{\hat{\phi }}_1\left(-n\right)E_{11}+{\hat{\phi }}_2\left(-n\right)E_{12}+{\hat{\phi }}_3\left(-n\right)E_{21}+{\hat{\phi }}_4\left(-n\right)E_{22}\right],n\in \mathbb{Z}.$

其中 ${\phi }_j\left(z\right)={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}\hat{\phi }}\left(n\right)z^n$，且 $z\in \mathbb{T}$， $j=1,2,3,4$。

推论3.2 假设 $\Phi =\left(\begin{array}{cc}{\phi }_1& {\phi }_2\\ \text{0}& {\phi }_4\end{array}\right)\in L^{\infty }\left(\mathbb{T}\right)\otimes M_2$， $T_{\Phi }=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\phi }_2}\\ 0& T_{{\phi }_4}\end{array}\right)$ 是关于共轭算子 $C_{\text{0}}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{C}_q& C_q\\ C_q& -C_q\end{array}\right)$ 的复对称算子当且仅当

$\left(\begin{array}{cc}{\hat{\phi }}_1\left(n\right)& {\hat{\phi }}_2\left(n\right)\\ 0& {\hat{\phi }}_4\left(n\right)\end{array}\right)=\frac{q_n}{q_0}\left(\begin{array}{cc}{\hat{\phi }}_1\left(-n\right)& {\hat{\phi }}_2\left(-n\right)\\ 0& {\hat{\phi }}_4\left(-n\right)\end{array}\right),$

其中 ${\phi }_j\left(z\right)={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}\hat{\phi }}\left(n\right)z^n,z\in \mathbb{T},j=1,2,4;n\in \mathbb{Z}$。

下面研究关于另一类共轭算子的2阶复对称块Toeplitz算子。

本文以下记

$C_{\text{00}}:=\left(\begin{array}{cc}0& C_q\\ C_q& 0\end{array}\right),$

显然其为共轭算子。

定理3.3 $T_{\Phi }=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\phi }_2}\\ T_{{\phi }_3}& T_{{\phi }_4}\end{array}\right)$ 是关于共轭算子 $C_{\text{00}}$ 的复对称算子当且仅当

${\hat{\phi }}_{\text{2}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{2}}\left(-n\right),{\hat{\phi }}_3\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_3\left(-n\right),{\hat{\phi }}_{\text{4}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{1}}\left(-n\right).$

其中 ${\phi }_j\left(z\right)={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}\hat{\phi }}\left(n\right)z^n,z\in \mathbb{T},j=1,2,4;n\in \mathbb{Z}$。

证明 由 $T_{\Phi }$ 是关于共轭算子 $C_{\text{00}}$ 的复对称算子当且仅当 $T_{{\phi }_2},T_{{\phi }_3}$ 关于 $C_q$ 是复对称的，且 $T_{{\phi }_4}=C_q{T}_{{\phi }_1}^{\ast }{C}_q$。又由定理2.8可得

$\{\begin{array}{l}{\hat{\phi }}_{\text{2}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{2}}\left(-n\right)\\ {\hat{\phi }}_3\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_3\left(-n\right)\\ {\hat{\phi }}_{\text{4}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{1}}\left(-n\right)\end{array}n\in \mathbb{Z}.$

4. 向量值Hardy空间的3阶复对称块Toeplitz算子

在前文的基础上，我们研究向量值Hardy空间上的3阶复对称块Toeplitz算子。本小节给出两个共轭算子，讨论关于这两类共轭算子的复对称块Toeplitz算子。

记 $C_{\text{1}}=\left(\begin{array}{ccc}{C}_q& 0& 0\\ 0& 0& C_q\\ 0& C_q& 0\end{array}\right)=\left(\begin{array}{cc}{C}_q& \\ & C_{\text{00}}\end{array}\right)$， $C_{\text{00}}=\left(\begin{array}{cc}0& C_q\\ C_q& 0\end{array}\right)$。由前面的讨论，显然 $C_{\text{1}}$ 是共轭算子。

命题4.1 假设 $\Phi \in L^{\infty }\left(\mathbb{T}\right)\otimes M_3$， ${\phi }_j\left(z\right)={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}\hat{\phi }}\left(n\right)z^n,j=1,\cdots ,6;z\in \mathbb{T}$， $T_{\Phi }=\left(\begin{array}{ccc}{T}_{{\phi }_1}& T_{{\phi }_4}& T_{{\phi }_6}\\ 0& T_{{\phi }_2}& T_{{\phi }_5}\\ 0& 0& T_{{\phi }_3}\end{array}\right)$ 是关于共轭算子 $C_{\text{1}}$ 的复对称算子当且仅当

$\left(\begin{array}{ccc}{\hat{\phi }}_1\left(n\right)& {\hat{\phi }}_4\left(n\right)& {\hat{\phi }}_6\left(n\right)\\ 0& {\hat{\phi }}_2\left(n\right)& {\hat{\phi }}_5\left(n\right)\\ 0& 0& {\hat{\phi }}_3\left(n\right)\end{array}\right)=\frac{q_n}{q_0}\left(\begin{array}{ccc}{\hat{\phi }}_1\left(-n\right)& 0& 0\\ 0& {\hat{\phi }}_3\left(-n\right)& {\hat{\phi }}_5\left(-n\right)\\ 0& 0& {\hat{\phi }}_2\left(-n\right)\end{array}\right)n\in \mathbb{Z}.$

证明 通过划分矩阵得

$T_{\Phi }=\left(\begin{array}{ccc}{T}_{{\phi }_1}& T_{{\phi }_4}& T_{{\phi }_6}\\ 0& T_{{\phi }_2}& T_{{\phi }_5}\\ 0& 0& T_{{\phi }_3}\end{array}\right)=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\Phi }_1}\\ 0& T_{{\Phi }_2}\end{array}\right),$

其中， $T_{{\Phi }_1}=\left(\begin{array}{cc}{T}_{{\phi }_4}& T_{{\phi }_6}\end{array}\right)$， $T_{{\Phi }_2}=\left(\begin{array}{cc}{T}_{{\phi }_2}& T_{{\phi }_5}\\ 0& T_{{\phi }_3}\end{array}\right)$。

因为 $T_{\Phi }$ 是关于 $C_{\text{1}}$ 的复对称算子， $T_{\Phi }{C}_{\text{1}}=C_{\text{1}}{T}_{\Phi }^{*}$，得

$T_{\Phi }{C}_{\text{1}}=\left(\begin{array}{cc}{T}_{{\phi }_1}& T_{{\Phi }_1}\\ 0& T_{{\Phi }_2}\end{array}\right)\left(\begin{array}{cc}{C}_q& \\ & C_{\text{00}}\end{array}\right)=\left(\begin{array}{cc}{T}_{{\phi }_1}{C}_q& T_{{\Phi }_1}{C}_{\text{00}}\\ 0& T_{{\Phi }_2}{C}_{\text{00}}\end{array}\right)\text{,}$ $C_{\text{1}}{T}_{\Phi }^{*}=\left(\begin{array}{cc}{C}_q& \\ & C_{\text{00}}\end{array}\right)\left(\begin{array}{cc}{T}_{{\phi }_1}^{*}& 0\\ T_{{\Phi }_1}^{*}& T_{{\Phi }_2}^{*}\end{array}\right)=\left(\begin{array}{cc}{C}_q{T}_{{\phi }_1}^{*}& 0\\ C_{\text{00}}{T}_{{\Phi }_1}^{*}& C_{\text{00}}{T}_{{\Phi }_2}^{*}\end{array}\right)\text{,}$

对比得

$\{\begin{array}{l}{T}_{{\phi }_1}{C}_q=C_q{T}_{{\phi }_1}^{\ast }\\ T_{{\Phi }_1}{C}_{\text{00}}=0\\ 0=C_{\text{00}}{T}_{{\Phi }_1}^{*}\\ T_{{\Phi }_2}{C}_{\text{00}}=C_{\text{00}}{T}_{{\Phi }_2}^{*}\end{array}$

由定理2.8和定理3.3，有

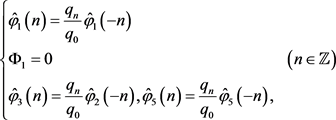
即

${\hat{\phi }}_{\text{1}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{1}}\left(-n\right),{\hat{\phi }}_{\text{3}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{2}}\left(-n\right),{\hat{\phi }}_4\left(n\right)\equiv 0,{\hat{\phi }}_{\text{5}}\left(n\right)=\frac{q_n}{q_0}{\hat{\phi }}_{\text{5}}\left(-n\right),{\hat{\phi }}_6\left(n\right)\equiv 0,$

对 $n\in \mathbb{Z}$ 成立。

同理可得以下推论，

推论4.2 假设 $\Phi \in L^{\infty }\left(\mathbb{T}\right)\otimes M_3$， ${\phi }_j\left(z\right)={\displaystyle \underset{n=-\infty }{\overset{\infty }{\sum }}\hat{\phi }}\left(n\right)z^n,j=1,\cdots ,7;z\in \mathbb{T}$， $T_{\Phi }=\left(\begin{array}{ccc}{T}_{{\phi }_1}& T_{{\phi }_4}& 0\\ T_{{\phi }_6}& T_{{\phi }_2}& T_{{\phi }_5}\\ 0& T_{{\phi }_7}& T_{{\phi }_3}\end{array}\right)$ 是关于共轭算子 $C_{\text{1}}$ 的复对称算子当且仅当

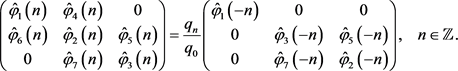
5. 向量值Hardy空间的n阶复对称块Toeplitz算子

本部分研究关于某个共轭算子 $C^{\prime }$ 的n阶复对称块Toeplitz算子。

记

$C^{\prime }={\left(\begin{array}{cccccc}0& C_q& 0& 0& \cdots & 0\\ C_q& 0& 0& 0& \cdots & 0\\ 0& 0& C_q& 0& \cdots & 0\\ 0& 0& 0& C_q& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & 0\\ 0& 0& 0& 0& 0& C_q\end{array}\right)}_{n\times n}=\left(\begin{array}{cc}{C}_{\text{00}}& 0\\ 0& {C^{″}}_{n-2}\end{array}\right),$

其中 ${C^{″}}_{n-2}={\left(\begin{array}{ccccc}{C}_q& & & & \\ & C_q& & & \\ & & \ddots & & \\ & & & \ddots & \\ & & & & C_q\end{array}\right)}_{\left(n-2\right)\times \left(n-2\right)}$ 是共轭算子。显然 $C^{\prime }$ 也是共轭算子。

命题5.1 假设 $\Phi \in L^{\infty }\left(\mathbb{T}\right)\otimes M_n$。 $T_{\Phi }=\left(\begin{array}{ccccc}{T}_{{\phi }_{11}}& T_{{\phi }_{12}}& T_{{\phi }_{13}}& \cdots & T_{{\phi }_{1n}}\\ 0& T_{{\phi }_{22}}& T_{{\phi }_{23}}& \cdots & T_{{\phi }_{2n}}\\ 0& 0& T_{{\phi }_{33}}& \cdots & T_{{\phi }_{3n}}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & T_{{\phi }_{nn}}\end{array}\right)$ 是关于共轭算子 $C^{\prime }$ 的复对称算子当且仅当

$\left(\begin{array}{ccccc}{\hat{\phi }}_{11}\left(k\right)& {\hat{\phi }}_{12}\left(k\right)& \cdots & \cdots & {\hat{\phi }}_{1n}\left(k\right)\\ & {\hat{\phi }}_{22}\left(k\right)& & & {\hat{\phi }}_{2n}\left(k\right)\\ & & \ddots & & ⋮\\ & & & \ddots & ⋮\\ & & & & {\hat{\phi }}_{nn}\left(k\right)\end{array}\right)=\left(\begin{array}{ccccc}{\hat{\phi }}_{22}\left(-k\right)& {\hat{\phi }}_{12}\left(-k\right)& 0& \cdots & 0\\ & {\hat{\phi }}_{11}\left(-k\right)& 0& \cdots & 0\\ & & {\hat{\phi }}_{33}\left(-k\right)& & 0\\ & & & \ddots & ⋮\\ & & & & {\hat{\phi }}_{nn}\left(-k\right)\end{array}\right)\left(k\in \mathbb{Z}\right).$

证明 对矩阵分块得

$\left(\begin{array}{ccccc}{T}_{{\phi }_{11}}& T_{{\phi }_{12}}& T_{{\phi }_{13}}& \cdots & T_{{\phi }_{1n}}\\ 0& T_{{\phi }_{22}}& T_{{\phi }_{23}}& \cdots & T_{{\phi }_{2n}}\\ 0& 0& T_{{\phi }_{33}}& \cdots & T_{{\phi }_{3n}}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & T_{{\phi }_{nn}}\end{array}\right)=\left(\begin{array}{cc}{T}_{{\Phi }_1}& T_{{\Phi }_2}\\ 0& T_{{\Phi }_3}\end{array}\right),$

其中 $T_{{\Phi }_1}=\left(\begin{array}{cc}{T}_{{\phi }_{11}}& T_{{\phi }_{12}}\\ 0& T_{{\phi }_{22}}\end{array}\right)$， $T_{{\Phi }_2}=\left(\begin{array}{cccc}{T}_{{\phi }_{13}}& T_{{\phi }_{14}}& \cdots & T_{{\phi }_{1n}}\\ T_{{\phi }_{23}}& T_{{\phi }_{24}}& \cdots & T_{{\phi }_{2n}}\end{array}\right)$， $T_{{\Phi }_3}=\left(\begin{array}{cccc}{T}_{{\phi }_{33}}& T_{{\phi }_{34}}& \cdots & T_{{\phi }_{3n}}\\ & T_{{\phi }_{44}}& \cdots & T_{{\phi }_{4n}}\\ & & \ddots & ⋮\\ & & & T_{{\phi }_{nn}}\end{array}\right)$。

因为 $T_{\Phi }$ 是关于 $C^{\prime }$ 的复对称算子，由于 $T_{\Phi }{C}^{\prime }=C^{\prime }{T}_{\Phi }^{*}$，对比可得

$\{\begin{array}{l}{T}_{{\Phi }_1}{C}_{\text{00}}=C_{\text{00}}{T}_{{\Phi }_1}^{*}\\ T_{{\Phi }_2}{C^{″}}_{n-2}=0\\ 0={C^{″}}_{n-2}{T}_{{\Phi }_2}^{*}\\ T_{{\Phi }_3}{C^{″}}_{n-2}={C^{″}}_{n-2}{T}_{{\Phi }_3}^{*}\end{array}$

进而

$\left(\begin{array}{cccc}{\hat{\phi }}_{13}\left(k\right)& {\hat{\phi }}_{14}\left(k\right)& \cdots & {\hat{\phi }}_{1n}\left(k\right)\\ {\hat{\phi }}_{23}\left(k\right)& {\hat{\phi }}_{24}\left(k\right)& \cdots & {\hat{\phi }}_{2n}\left(k\right)\end{array}\right)=\left(\begin{array}{cccc}0& 0& \cdots & 0\\ 0& 0& \cdots & 0\end{array}\right).$

和

${\hat{\phi }}_{ii}\left(k\right)=\frac{q_k}{q_0}{\hat{\phi }}_{ii}\left(-k\right),i=3,4,\cdots ,n\left(k\in \mathbb{Z}\right).$

由定理2.8和定理3.3可得

$\left(\begin{array}{cc}{\hat{\phi }}_{11}\left(k\right)& {\hat{\phi }}_{12}\left(k\right)\\ 0& {\hat{\phi }}_{22}\left(k\right)\end{array}\right)=\frac{q_k}{q_0}\left(\begin{array}{cc}{\hat{\phi }}_{22}\left(-k\right)& {\hat{\phi }}_{12}\left(-k\right)\\ 0& {\hat{\phi }}_{11}\left(-k\right)\end{array}\right).$

所以

$\left(\begin{array}{ccccc}{\hat{\phi }}_{11}\left(k\right)& {\hat{\phi }}_{12}\left(k\right)& \cdots & \cdots & {\hat{\phi }}_{1n}\left(k\right)\\ & {\hat{\phi }}_{22}\left(k\right)& & & {\hat{\phi }}_{2n}\left(k\right)\\ & & \ddots & & ⋮\\ & & & \ddots & ⋮\\ & & & & {\hat{\phi }}_{nn}\left(k\right)\end{array}\right)=\frac{q_k}{q_0}\left(\begin{array}{ccccc}{\hat{\phi }}_{22}\left(-k\right)& {\hat{\phi }}_{12}\left(-k\right)& 0& \cdots & 0\\ & {\hat{\phi }}_{11}\left(-k\right)& 0& \cdots & 0\\ & & {\hat{\phi }}_{33}\left(-k\right)& & 0\\ & & & \ddots & ⋮\\ & & & & {\hat{\phi }}_{nn}\left(-k\right)\end{array}\right),$

对于 $k\in \mathbb{Z}$ 成立。

6. 结论与展望

本文研究了向量值Hardy空间中的复对称块Toeplitz算子问题，利用 $C_q$ 构造了不同的块共轭算子，描述出2阶、3阶和n阶复对称块Toeplitz算子 $T_{\Phi }$ 的符号特征。

应用本文方法还会得到其他复对称块Toeplitz算子的实例。在以后的研究中，会有更复杂的共轭算子，进而可以更加深入地研究复对称块Toeplitz算子问题。