一类带有时滞效应的修正的Leslie-Gower捕食者–食饵模型动力学分析

Dynamics Analysis of a Modified Leslie-Gower Predator-Prey Model with Time Delay

摘要: 本文构建了一类带有时滞效应的修正的Leslie-Gower捕食者–食饵模型，旨在研究时滞效应对捕食者–食饵模型动力学性质的影响。运用时滞微分方程理论，分析了模型中由时滞导致的Hopf分岔的存在性。借助于中心流形定理和规范型理论进一步推导Hopf分岔的方向以及周期解的稳定性。此外，数值模拟揭示了种群的密度与平衡点的稳定性对Allee效应、食饵避难以及时滞的变化具有一定的敏感性。

Abstract: This paper constructs a modified Leslie-Gower predator-prey model with Allee effect and prey refuge. The aim of this paper is to study the effect of time delay on the population dynamics. By using delay differential equation theory, we demonstrate the existence of Hopf bifurcation which is induced by time delay. According to center manifold theorem and normal form theory, the direction of Hopf bifurcation and stability of periodic solution are discussed. Additionally, numerical simulations reveal that the population density and the stability of positive equilibrium are sensitive for variations of time delay, Allee effect and prey refuge.

1. 引言

由于捕食现象在自然界中的重要性和普遍存在性，捕食者和食饵种群之间的动力学性质一直是生物数学领域研究的重要课题之一。在过去的几十年里，捕食者–食饵模型被广泛的研究并得到了许多有趣的结果 [1] [2] [3] [4]。例如Leslie [5] 和Gower [6] 建立了如下经典的Leslie-Gower捕食模型：

$\{\begin{array}{l}\frac{\text{d}u}{\text{d}t}=u\left(r_1-a_{1}u-c_{1}v\right)\\ \frac{\text{d}v}{\text{d}t}=v\left(r_2-\frac{c_{2}v}{u}\right)\end{array}$ (1.1)

其中， $\frac{c_{2}v}{u}$ 为Leslie-Gower项。众多学者对模型(1.1)做了改进和研究 [7] [8] [9]，如Aziz-Alaoui和Okiye

考虑到捕食者在其偏好食饵种群缺乏的区域会转向其他食饵种群，从而提出了修正的Leslie-Gower捕食者–食饵模型 [10]。该模型使得经典的Leslie-Gower模型的局限性得到修正，从而吸引了众多研究者的关注 [11] [12] [13]。基于修正的Leslie-Gower模型，许多不同的因素如脉冲、扩散、随机等被引入模型中进行研究得到了大量的研究成果 [14] [15] [16] [17]。特别地，Ningjin等人 [18] 将时滞因素引入修正的Leslie-Gower捕食者–食饵模型中，通过分析平衡点的全局渐近稳定性，发现时滞会导致正平衡点失稳。

事实上，时滞在种群的动力学研究中非常常见。在自然界中，生物种群对于某些环境的变化或者种群之间的相互作用无法做出即时的反应，如从捕食者捕获食饵到转化为自身的能量需要一定的时间即消化时滞、从幼体的孕育到出生过程存在妊娠周期即妊娠时滞。为了刻画过去的状态对捕食者–食饵种群的影响，人们在捕食者–食饵模型中引入时滞项。1948年，Wright首次提出时滞的概念并将时滞引入模型中 [19]，直到1973年May将时滞项纳入捕食者–食饵模型中研究，结果表明时滞会改变系统的稳定性 [20]。此后，对于时滞的研究吸引了众多学者的兴趣。Yafia等人 [21] 在带有时滞的修正的Leslie-Gower模型中，证明了极限环的存在性。Celik等人 [22] 证明了由时滞导致的Hopf分岔，并进一步推导了分岔的方向与周期解的稳定性。Shu等人 [23] 研究了由时滞导致的稳定性转换、多重失稳与混沌现象。这些研究成果表明时滞效应在种群动力学研究中不容忽视，带有时滞因素的模型动力学性质也更加复杂。

此外，现实生态系统中还存在许多影响捕食者和食饵种群互作关系的因素如Allee效应与食饵避难等。大量的研究表明Allee效应能够丰富模型的动力学性质 [24] [25] [26] [27]；食饵种群的避难行为会影响系统的稳定性与种群密度的变化 [28] [29] [30]。然而，目前综合考虑Allee效应、食饵避难与时滞因素的研究工作较少。因此，为了研究这些不同因素对捕食者–食饵模型动力学性质的重要影响，本文建立了如下带有时滞的修正的Leslie-Gower模型：

$\{\begin{array}{l}\frac{\text{d}u}{\text{d}t}=u\left(r_1-a_{1}u-\frac{h}{b+u}-c_1\left(1-m\right)v\right)\\ \frac{\text{d}v}{\text{d}t}=v\left(r_2-\frac{c_{2}v\left(t-\tau \right)}{\left(1-m\right)u\left(t-\tau \right)+k}\right)\end{array}$ (1.2)

这里， $\tau$ 为考虑捕食者种群妊娠期的时滞，u和v分别表示食饵和捕食者种群的密度， $r_1$ 为食饵种群的内禀增长率， $r_2$ 为捕食者种群的内禀增长率， $a_1$ 表示食饵种群内部的竞争引起的内禀增长率的减少，h和b为Allee效应常数， $c_1$ 表示捕食者对食饵的捕食率，m代表食饵避难率并且 $m\in \left(0,1\right)$，k表示环境为捕食者种群所提供的保护。 $\frac{hu}{b+u}$ 为加性Allee效应， $\frac{c_{2}v}{\left(1-m\right)u+k}$ 是考虑了食饵避难效应的修正的Leslie-Gower项。

本文主要内容组织如下：第二部分为模型的动力学性质分析主要包括正平衡点的存在性与稳定性、Hopf分岔分析以及分岔的方向与周期解的稳定性；第三部分为数值模拟主要包括时序图、相图以及敏感性分析；第四部分为本文的主要结论。

2. 动力学性质

2.1. 正平衡点的存在性与稳定性

为了讨论时滞效应对模型(1.2)动力学性质的影响，我们首先分析模型(1.2)所对应的正平衡点的存在性与稳定性。

令

$A=-a_1{c}_2-c_1{\left(1-m\right)}^2{r}_2$

$D=b{r}_1{c}_2-h{c}_2-b{c}_{1}k\left(1-m\right)r_2,$

$B=r_1{c}_2-b{a}_1{c}_2-b{c}_1{\left(1-m\right)}^2{r}_2-c_{1}k\left(1-m\right)r_2.$

并给出如下条件：

$H_1:m<\frac{h{c}_2+c_{1}k{r}_2-r_1{c}_2}{k{c}_1{r}_2},B>0,\Delta =B^2-4AD>0.$

经过计算可知，当条件 成立时，模型(1.2)存在两个正平衡点 $E_4=\left(u_4,v_4\right)$ 和 $E_5=\left(u_5,v_5\right)$。其中，

$u_4=\frac{-B+\sqrt{B^2-4AD}}{2A},v_4=\frac{r_2\left(\left(1-m\right)u_4+k\right)}{c_2}$

$u_5=\frac{-B-\sqrt{B^2-4AD}}{2A},v_4=\frac{r_2\left(\left(1-m\right)u_5+k\right)}{c_2}$

下面讨论正平衡点 $E_4,E_5$ 的局部渐近稳定性。容易算得模型(1.2)在平衡点 $E_4,E_5$ 处的雅可比矩阵：

$J_{E_i}=\left(\begin{array}{cc}{u}_i\left(\frac{h}{{\left(b+u_i\right)}^2}-a_1\right)& -c_1\left(1-m\right)u_i\\ \frac{r_2^2\left(1-m\right)}{c_2}& -r_2\end{array}\right),i=4,5$

显然，

$tr\left(J_{E_i}\right)=u_i\left(\frac{h}{{\left(b+u_i\right)}^2}-a_1\right)-r_2,$ (2.1.1)

$det\left(J_{E_i}\right)=\frac{u_i{r}_2}{c_2{\left(b+u_i\right)}^2}\left(\left(a_1{c}_2+c_1{\left(1-m\right)}^2{r}_2\right){\left(b+u_i\right)}^2-h{c}_2\right).$ (2.1.2)

令

$G\left(u\right)=\left(\left(a_1{c}_2+c_1{\left(1-m\right)}^2{r}_2\right){\left(b+u_i\right)}^2-h{c}_2\right),$

计算可知， $G\left(u\right)=0$ 存在一个正根

$P_1=\frac{2bA+\sqrt{-4h{c}_{2}A}}{-2A}.$

由于 $G\left(u_4\right)<G\left(P_1\right)=0$，因此可以得到 $det\left(J_{E_4}\right)<0$，即 $E_4$ 恒为不稳定平衡点。类似地，我们可以得出 $det\left(J_{E_5}\right)>0$。即 $E_5$ 的局部渐近稳定性取决于 $tr\left(J_{E_i}\right)$ 的正负。将方程(2.1.1)整理为如下形式

$tr\left(J_{E_5}\right)=\frac{-1}{8{\left(b+u_5\right)}^2{A}^3}\left[L_1-L_2\sqrt{{\left(E-bA\right)}^2+4h{c}_{2}A}\right],$

其中，

$L_1=h\left[4A^2\left(\left(E+bA\right)+2r_2{c}_2+b{a}_1{c}_2\right)-12AE{a}_1{c}_2\right]+4{\left(E-bA\right)}^2\left(A{r}_2-a_{1}E\right),$

$L_2=h\left[-4A^2+4A{a}_1{c}_2\right]+4\left(E-bA\right)\left(a_{1}E-A{r}_2\right),$

$E=r_1{c}_2-c_{1}k\left(1-m\right)r_2.$

由 $A<0$ 可知 $tr\left(J_{E_5}\right)$ 的符号与函数 $L_1-L_2\sqrt{{\left(E-bA\right)}^2+4h{c}_{2}A}$ 一致。

经过计算，存在正根 $h_1,h_2$ 使得 $L_1\left(h_1\right)=0,L_2\left(h_2\right)=0$，其中，

$h_1=\frac{-4{\left(E-bA\right)}^2\left(A{r}_2-a_{1}E\right)}{4A^2\left(\left(E+bA\right)+2r_2{c}_2+b{a}_1{c}_2\right)-12AE{a}_1{a}_2},$

$h_2=\frac{-4\left(E-bA\right)\left(a_{1}E-A{r}_2\right)}{-4A^2+4A{a}_1{c}_2}.$

根据 $h_1$ 与 $h_2$ 的大小，我们分为下面两种情况来讨论。

1) $h_2>h_1$

在此条件下，当 $h>h_2$，可以推出 $L_1>0,L_2<0$，进而得出 $tr\left(J_{E_5}\right)>0$，即平衡点 $E_5$ 不稳定；当 $h<h_1$，可以推出 $L_1<0,L_2>0$，进而得出 $tr\left(J_{E_5}\right)<0$，即平衡点 $E_5$ 局部渐近稳定；当 $h_1<h<h_2$ 时， $tr\left(J_{E_5}\right)$ 的符号与函数 $L_1^2-L_2^2\left({\left(E-bA\right)}^2+4h{c}_{2}A\right)$ 保持一致。

经计算，

$L_1^2-L_2^2\left({\left(E-bA\right)}^2+4h{c}_{2}A\right)=h^2\left(-4A{c}_2{\left(4A{a}_1{c}_2-4A^2\right)}^2\right)+h{M}_1+M_2,$

其中，

$M_1=64A^3\left[\left(a_{1}b-r_2\right)\left(E{a}_1-A{r}_2\right)c_2^2+\left(b{A}^2\left(a_{1}b+3r_2\right)-4EA\left(a_{1}b+\frac{1}{4}{r}_2\right)+E^2{a}_1\right)c_2+A^{2}Eb\right],$

$M_2=64A^6{b}^3{r}_2-64A^{5}E{b}^2{r}_2-128A^4{E}^{2}b{r}_2+128A^4{E}^{2}b{r}_2-64A^3{E}^3{a}_{1}b.$

令

${\Delta }_1=M_1^2+16M_{2}A{c}_2{\left(4A{a}_1{c}_2-4A^2\right)}^2.$

容易看出 $M_2>0$，那么当 $M_1<0,{\Delta }_1>0$ 时，存在 $h_3,h_4$ 使得 $L_1^2-L_2^2\left({\left(E-bA\right)}^2+4h{c}_{2}A\right)$ 有两个零点分别为

$h_3=\frac{-M_1-\sqrt{{\Delta }_1}}{-8A{c}_2{\left(4A{a}_1{c}_2-4A^2\right)}^2},h_4=\frac{-M_1+\sqrt{{\Delta }_1}}{-8A{c}_2{\left(4A{a}_1{c}_2-4A^2\right)}^2}.$

因此，当 $M_1<0,{\Delta }_1>0,h_3<h<h_4$ 时， $L_1^2-L_2^2\left({\left(E-bA\right)}^2+4h{c}_{2}A\right)<0$。也即平衡点 $E_5$ 局部渐近稳定。

2) $h_2<h_1$

类似地，我们可以得出当 $h>h_1$，有 $tr\left(J_{E_5}\right)>0$ ；当 $0<h<h_2$，有 $tr\left(J_{E_5}\right)<0$ ；当 $h_2<h<h_1$ 时，则 $tr\left(J_{E_5}\right)$ 的符号与函数 $L_1^2-L_2^2\left({\left(E-bA\right)}^2+4h{c}_{2}A\right)$ 相反。

根据(1)中的分析可知，当下列条件(i)、(ii)、(iii)中任一条满足时，有 $L_1^2-L_2^2\left({\left(E-bA\right)}^2+4h{c}_{2}A\right)>0$，即平衡点 $E_5$ 局部渐近稳定。

i) $M_1>0$ ；ii) $M_1<0,{\Delta }_1<0$ ；iii) $M_1<0,{\Delta }_1>0,h\in \left(0,h_3\right)\cup \left(h_4,+\infty \right)$

因此。得到定理2.1，如下：

定理2.1当条件 $H_1$ 成立时，模型(2-1)存在两个正平衡点 $E_4$ 和 $E_5$，并且 $E_4$ 恒为不稳定的平衡点。平衡点 $E_5$ 是局部渐近稳定当且仅当下列条件中的任意一条满足，

a) $h_2>h_1,0<h<h_1$，(b) $h_2>h_1,h_1<h<h_2,M_1<0,{\Delta }_1>0,h_3<h<h_4$，

c) $h_2<h_1,0<h<h_2$，(d) $h_2<h_1,M_1>0,h_2<h<h_1$，

e) $h_2<h_1,M_1<0,h_2<h<h_1,{\Delta }_1>0,h\in \left(0,h_3\right)\cup \left(h_4,+\infty \right)$，

f) $h_2<h_1,M_1<0,h_2<h<h_1,{\Delta }_1<0$。

2.2. Hopf分岔

本小节主要研究模型(1.2)中Hopf分岔的存在性。

首先将平衡点 $E_5$ 平移至原点，令

$\{\begin{array}{l}x\left(t\right)=u\left(t\right)-u_5\\ y\left(t\right)=v\left(t\right)-v_5\end{array}$

将模型(1.2)化为

$\{\begin{array}{l}\frac{\text{d}x\left(t\right)}{\text{d}t}=a_{11}x\left(t\right)+a_{12}y\left(t\right)\\ \frac{\text{d}y\left(t\right)}{\text{d}t}=a_{21}x\left(t-\tau \right)+a_{22}y\left(t-\tau \right)+a_{23}y\left(t\right)\end{array}$ (2.2.1)

其中，

$a_{11}=u_5\left(\frac{h}{{\left(b+u_5\right)}^2}-a_1\right),a_{12}=-c_1\left(1-m\right)u_5,$

$a_{21}=\frac{r_2^2\left(1-m\right)}{c_2},a_{22}=-r_2,a_{23}=0.$

模型(2.2.1)对应的雅可比矩阵如下

$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}{\text{e}}^{-\lambda \tau }& a_{22}{\text{e}}^{-\lambda \tau }\end{array}\right]$

则特征方程为

${\lambda }^2-\left(a_{11}+a_{22}{\text{e}}^{-\lambda \tau }\right)\lambda +\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right){\text{e}}^{-\lambda \tau }=0.$ (2.2.2)

显然，当 $\tau =0$ 时，如果定理3.1中条件(a)~(f)中任一条满足，则方程(2.2.2)的所有根都具有负实部。当 $\tau >0$ 时，设存在一对纯虚根 $\lambda =\pm i\omega \left(\tau \right)\left(\omega >0\right)$，将其带入方程(2.2.2)并分离实虚部可得：

$\{\begin{array}{l}-{\omega }^2\left(\tau \right)+a_{22}\omega \left(\tau \right)\sin \omega \tau +\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)\cos \omega \tau =0\\ -a_{11}\omega \left(\tau \right)-a_{22}\omega \left(\tau \right)\cos \omega \tau +\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)\sin \omega \tau =0\end{array}$ (2.2.3)

经过化简得到：

${\omega }^4\left(\tau \right)+\left(a_{11}^2-a_{22}^2\right){\omega }^2\left(\tau \right)-{\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2=0.$ (2.2.4)

不难看出，方程(2.2.4)存在唯一的一个正根

${\omega }_0=\sqrt{\frac{\left(a_{22}^2-a_{11}^2\right)+\sqrt{{\left(a_{22}^2-a_{11}^2\right)}^2+4{\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2}}{2}}$ .

利用方程(2.2.3)可以求出：

$\cos {\omega }_0\tau =\frac{-{\omega }_0^2{a}_{21}{a}_{12}}{a_{22}^2{\omega }_0^2+{\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2},$

进一步得到，

${\tau }_j=\frac{1}{{\omega }_0}\arccos \frac{-{\omega }_0^2{a}_{21}{a}_{12}}{a_{22}^2{\omega }_0^2+{\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2}+\frac{2j\pi }{{\omega }_0},j=0,1,2,\cdots .$

显然， ${\tau }_0=\min \left\{{\tau }_j,j=0,1,2,\cdots \right\}$。下面证明Hopf分岔的横截性条件成立。

对方程(2.2.2)两边关于时滞参数 $\tau$ 求导：

${\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}=\left(\frac{2\lambda -a_{11}}{\lambda \left(a_{11}\lambda -{\lambda }^2\right)}-\frac{\tau }{\lambda }-\frac{a_{22}}{\lambda \left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)-a_{22}{\lambda }^2}\right).$

将 $\tau ={\tau }_0$ 代入上述方程 ${\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}$ 中，通过分离实部与虚部可得

${Re{\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}|}_{\tau ={\tau }_0}=\frac{a_{11}^2{\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2+2{\omega }_0^2{\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2+a_{22}^2{\omega }_0^4}{\left(a_{11}^2{\omega }_0^2+{\omega }_0^4\right)\left({\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)}^2+a_{22}^2{\omega }_0^2\right)}>0.$

易知 $sign{\left\{\frac{\text{d}\left(Re\left(\lambda \right)\right)}{\text{d}\tau }\right\}}_{\tau ={\tau }_0}=sign{\left\{Re{\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}\right\}}_{\tau ={\tau }_0}$，即横截性条件满足。

若条件 $H_1$ 成立，当定理2.1的条件(a)~(f)中任一条满足时，有如下定理：

定理2.2 当 $\tau <{\tau }_0$ 时，正平衡点 $E_5$ 是局部渐近稳定的；当 $\tau ={\tau }_0$ 时，模型(1.2)在 $E_5$ 处经历Hopf分岔；当 $\tau >{\tau }_0$ 时，平衡点 $E_5$ 是不稳定的。

2.3. Hopf分岔方向

小节2.2证明了，当 $\tau ={\tau }_j,j=0,1,2,\cdots$ 时，模型(1.2)在 $E_5$ 处经历了Hopf 分岔。因此，本小节主要利用中心流形定理与规范型理论来讨论Hopf分岔的方向以及相应周期解的稳定性。

首先做下列变换，

$x\left(t\right)=u\left(t\tau \right)-u_5,y\left(t\right)=v\left(t\tau \right)-v_5,$

$\tau ={\tau }_0+\delta ,\varphi ={\left(x,y\right)}^{\text{T}},{\varphi }_t\left(\theta \right)=\varphi \left(t+\theta \right),\theta \in \left[-1,0\right].$

将模型(1.2)化为

$\left(\begin{array}{c}\frac{\text{d}x}{\text{d}t}\\ \frac{\text{d}y}{\text{d}t}\end{array}\right)=\tau \left(B_1\left(\begin{array}{c}x\left(t\right)\\ y\left(t\right)\end{array}\right)+B_2\left(\begin{array}{c}x\left(t-1\right)\\ y\left(t-1\right)\end{array}\right)+f\right)$ (2.3.1)

这里， $B_1=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ 0& 0\end{array}\right],B_2=\left[\begin{array}{cc}0& 0\\ a_{21}& a_{22}\end{array}\right],f=f\left(\delta \right)\varphi =\left(\begin{array}{c}{f}_1\\ f_2\end{array}\right)$ 。

其中，

$a_{11}=-a_1{u}_5+\frac{h{u}_5}{{\left(b+u_5\right)}^2},a_{12}=-c_1\left(1-m\right)u_5,$

$a_{21}=\frac{r_2^2\left(1-m\right)}{c_2},a_{22}=-r_2.$

$f_1=\left(\frac{hb}{{\left(b+u_5\right)}^3}-a_1\right)x^2\left(t\right)-c_1\left(1-m\right)x\left(t\right)y\left(t\right),$

$\begin{array}{c}{f}_2=-\frac{{\left(1-m\right)}^2{r}_2^2}{c_2\left(\left(1-m\right)u_5+k\right)}{x}^2\left(t-1\right)+\frac{r_2\left(1-m\right)}{\left(1-m\right)u_5+k}x\left(t-1\right)y\left(t\right)\\ +\frac{r_2\left(1-m\right)}{\left(1-m\right)u_5+k}x\left(t-1\right)y\left(t-1\right)-\frac{c_2}{\left(1-m\right)u_5+k}y\left(t\right)y\left(t-1\right).\end{array}$

由Riesz表示定理，存在二阶矩阵 $\eta \left(\theta ,\delta \right),\theta \in \left[-1,0\right]$，使得

$L_{\delta }\left(\varphi \right)={\displaystyle {\int }_{-1}^0\text{d}\eta }\left(\theta ,\delta \right)\varphi \left(\theta \right),\varphi \in C\left(\left[-1,0\right],R^2\right).$

选取

$\eta \left(\theta ,\delta \right)={\tau }_0+\delta \left[B_1\kappa \left(\theta \right)-B_2\kappa \left(\theta +1\right)\right].$

其中 $\kappa$ 是Dirac-Delta函数

$\kappa \left(\theta \right)=\{\begin{array}{l}0\theta \ne 0\\ 1\theta =0\end{array}$

对于 $\theta \in C\left(\left[-1,0\right],R^2\right)$，定义

$P\left(\delta \right)\varphi \left(\theta \right)=\{\begin{array}{l}\frac{\text{d}\varphi \left(\theta \right)}{\text{d}\theta },-1\le \theta <0\\ {\displaystyle {\int }_{-1}^0\text{d}\eta }\left(s,\delta \right)\varphi \left(s\right),\theta =0\end{array}$

$Q\left(\delta \right)\varphi \left(\theta \right)=\{\begin{array}{l}0-1\le \theta <0\\ f\left(\delta \right)\varphi \theta =0\end{array}$

将方程(2.3.1)化为如下形式

$\frac{\text{d}U}{\text{d}t}=P\left(\delta \right)U_t+Q\left(\delta \right)U_t$ (2.3.2)

其中，

$U={\left(x,y\right)}^{\text{T}},U\left(t\right)=U\left(t+\theta \right),\theta \in \left[-1,0\right]$

对于 $\psi \in C\left(\left[-1,0\right],{\left(R^2\right)}^{*}\right)$，定义

$P^{*}\psi \left(s\right)=\{\begin{array}{l}-\frac{\text{d}\psi \left(s\right)}{\text{d}s},0<s\le 1\\ {\displaystyle {\int }_{-1}^0\text{d}\eta }\left(0,\varsigma \right)\psi \left(-\varsigma \right),s=0\end{array}$

并定义双线性内积：

$\langle \psi \left(s\right),\varphi \left(\theta \right)\rangle =\bar{\psi }\left(0\right)\varphi \left(0\right)-{\displaystyle {\int }_{-1}^0{\displaystyle {\int }_{\varsigma =0}^{\theta }\bar{\psi }}}\left(\varsigma -\theta \right)\text{d}\eta \left(\theta \right)\varphi \left(\varsigma \right).$

这里， $\eta \left(\theta \right)=\eta \left(\theta ,0\right)$。由于 $\pm i{\tau }_0{\omega }_0$ 是P的特征值，故 $\pm i{\tau }_0{\omega }_0$ 也是 $P^{*}$ 的特征值。

令 $P\left(0\right)$ 对应特征值 $i{\tau }_0{\omega }_0$ 的特征向量为 $q\left(\theta \right)$， $P^{*}$ 对应特征值 $-i{\tau }_0{\omega }_0$ 的特征向量为 $q^{*}(\; s\; )$

$q\left(\theta \right)={\left(1,\alpha \right)}^{\text{T}}{\text{e}}^{i{\omega }_0{\tau }_0\theta },q^{*}\left(s\right)=D{\left(1,\beta \right)}^{\text{T}}{\text{e}}^{i{\omega }_0{\tau }_{0}s}.$

根据

$P\left(0\right)q\left(\theta \right)=q\left(\theta \right)i{\tau }_0{\omega }_0.$

可得

$\left[i{\omega }_{0}I-\left(K_1+K_2\right){\text{e}}^{-i{\omega }_0{\tau }_0}\right]q\left(0\right)=0.$

进一步有

$\left[\begin{array}{cc}i{\omega }_0-a_{11}& -a_{12}\\ -a_{21}{\text{e}}^{-i{\omega }_0{\tau }_0}& i{\omega }_0-a_{22}{\text{e}}^{-i{\omega }_0{\tau }_0}\end{array}\right]\left(\begin{array}{c}1\\ \alpha \end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right),$

和

$\left[\begin{array}{cc}i{\omega }_0+a_{11}& a_{21}{\text{e}}^{-i{\omega }_0{\tau }_0}\\ a_{12}& i{\omega }_0+a_{22}{\text{e}}^{-i{\omega }_0{\tau }_0}\end{array}\right]\left(\begin{array}{c}1\\ \beta \end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right).$

从而计算出

$\alpha =\frac{i{\omega }_0-a_{11}}{a_{12}},\beta =-\frac{\left(i{\omega }_0+a_{11}\right){\text{e}}^{i{\tau }_0{\omega }_0}}{a_{21}}.$

进而得到

$\begin{array}{c}{q}^{*}\left(s\right),q\left(\theta \right)={\bar{q}}^{*}\left(0\right)q\left(0\right)-{\displaystyle {\int }_{-1}^0{\displaystyle {\int }_0^{\theta }{\bar{q}}^{*}}}\left(\varsigma -\theta \right)\text{d}\eta \left(\theta \right)q\left(\varsigma \right)\text{d}\varsigma \\ =\bar{D}\left(\begin{array}{cc}1& \bar{\beta }\end{array}\right)\left(\begin{array}{c}1\\ \alpha \end{array}\right)-{\displaystyle {\int }_{-1}^0{\displaystyle {\int }_0^{\theta }\bar{D}}}\left(\begin{array}{cc}1& \bar{\beta }\end{array}\right){\text{e}}^{-i{\omega }_0{\tau }_0\left(\varsigma -\theta \right)}\text{d}\eta \left(\theta \right)\left(\begin{array}{c}1\\ \alpha \end{array}\right){\text{e}}^{-i{\omega }_0{\tau }_0\varsigma }\text{d}\varsigma \\ =\bar{D}\left(1+\alpha \bar{\beta }\right)+{\tau }_0\bar{D}{\text{e}}^{-i{\tau }_0{\omega }_0}\left(\frac{\bar{\beta }{r}_2^2\left(1-m\right)}{c_2}-\bar{\beta }{r}_2\alpha \right).\end{array}$

故取

$D={\left(1+\bar{\alpha }\beta +{\tau }_{\text{0}}{\text{e}}^{i{\tau }_0{\omega }_0}\left(\frac{\beta r_2^2\left(1-m\right)}{c_2}-\beta r_2\bar{\alpha }\right)\right)}^{-1},$

使得

$\langle q^{*}\left(s\right),q\left(\theta \right)\rangle =1,\langle q^{*}\left(s\right),\bar{q}\left(\theta \right)\rangle =0.$

定义

$z\left(t\right)=\langle q^{*},U_t\rangle ,W\left(t,\theta \right)=U_t\left(\theta \right)-2Re\left\{z\left(t\right)q\left(\theta \right)\right\},$ (2.3.3)

其中， $U_t$ 表示方程(2.3.3)在 $\delta =0$ 时的解。

在中心流形 $C_0$ 处有

$W\left(t,\theta \right)=W\left(z,\bar{z},\theta \right)=W_{20}\left(\theta \right)\frac{z^2}{2}+W_{11}\left(\theta \right)z\bar{z}+W_{02}\left(\theta \right)\frac{{\bar{z}}^2}{2}+W_{30}\left(\theta \right)\frac{z^3}{6}+\cdots$ (2.3.4)

其中，z和 $\bar{z}$ 表示 $C_0$ 在方向 $q^{*}$ 和 $\overline{q^{*}}$ 上的局部坐标。

当 $\delta =0$ 时，对于 $U_t\in C_0$，有下式成立：

$\begin{array}{l}\frac{\text{d}z\left(t\right)}{\text{d}t}=\langle q^{*},\stackrel{\dot{}}{U}\left(t\right)\rangle =i{\omega }_0{\tau }_{0}z\left(t\right)+\langle {\bar{q}}^{*}\left(\theta \right),Q\left(0\right)\left(W\left(z,\bar{z},\theta \right)+2Re\left\{z\left(t\right)q\left(\theta \right)\right\}\right)\rangle \\ ={\bar{q}}^{*}\left(0\right)f\left(0\right)\left(W\left(z,\bar{z},0\right)+2Re\left\{z\left(t\right)q\left(0\right)\right\}\right)\\ \triangleq i{\omega }_0{\tau }_{0}z\left(t\right)+g\left(z,\bar{z}\right).\end{array}$

其中，

$\begin{array}{c}g\left(z,\bar{z}\right)={\bar{q}}^{*}\left(0\right)f\left(0\right)\left(W\left(z,\bar{z},0\right)+2Re\left\{z\left(t\right)q\left(0\right)\right\}\right)=\bar{D}{\tau }_0\left(f_1+\bar{\beta }{f}_2\right)\\ =g_{20}\frac{z^2}{2}+g_{11}z\bar{z}+g_{02}\frac{{\bar{z}}^2}{2}+g_{21}\frac{z^2\bar{z}}{2}+\cdots \end{array}$ (2.3.5)

由于

$q\left(0\right)={\left(1,\alpha \right)}^{\text{T}},$

$\begin{array}{c}{U}_t\left(\theta \right)={\left(x_t\left(\theta \right),y_t\left(\theta \right)\right)}^{\text{T}}=2Re\left\{z\left(t\right)q\left(\theta \right)\right\}+W\left(t,\theta \right)\\ =zq\left(\theta \right)+\bar{z}\bar{q}\left(\theta \right)+W\left(t,\theta \right).\end{array}$

可得

$x\left(t\right)=z+\bar{z}+W_{20}^{\left(1\right)}\left(0\right)\frac{z^2}{2}+W_{11}^{\left(1\right)}\left(0\right)z\bar{z}+W_{02}^{\left(1\right)}\left(0\right)\frac{{\bar{z}}^2}{2},$

$y\left(t\right)=\alpha z+\bar{\alpha }\bar{z}+W_{20}^{\left(2\right)}\left(0\right)\frac{z^2}{2}+W_{11}^{\left(2\right)}\left(0\right)z\bar{z}+W_{02}^{\left(2\right)}\left(0\right)\frac{{\bar{z}}^2}{2},$

$x\left(t-1\right)=z{\text{e}}^{-i{\omega }_0{\tau }_0}+\bar{z}{\text{e}}^{i{\omega }_0{\tau }_0}+W_{20}^{\left(1\right)}\left(-1\right)\frac{z^2}{2}+W_{11}^{\left(1\right)}\left(-1\right)z\bar{z}+W_{02}^{\left(1\right)}\left(-1\right)\frac{{\bar{z}}^2}{2},$

$y\left(t-1\right)=\alpha z{\text{e}}^{-i{\omega }_0{\tau }_0}+\bar{\alpha }\bar{z}{\text{e}}^{i{\omega }_0{\tau }_0}+W_{20}^{\left(2\right)}\left(-1\right)\frac{z^2}{2}+W_{11}^{\left(2\right)}\left(-1\right)z\bar{z}+W_{02}^{\left(2\right)}\left(-1\right)\frac{{\bar{z}}^2}{2}.$

通过计算 $g\left(z,\bar{z}\right)$ 并比较系数可得

$g_{20}=2\bar{D}{\tau }_0\left[f_{11}+f_{12}\alpha +f_{21}\bar{\beta }{\text{e}}^{-2i{\omega }_0{\tau }_0}+f_{22}\bar{\beta }\alpha {\text{e}}^{-i{\omega }_0{\tau }_0}+f_{23}\bar{\beta }\alpha {\text{e}}^{-2i{\omega }_0{\tau }_0}+f_{24}{\alpha }^2\bar{\beta }{\text{e}}^{-i{\omega }_0{\tau }_0}\right],$

$\begin{array}{c}{g}_{11}=\bar{D}{\tau }_0[2f_{11}+f_{12}\left(\bar{\alpha }+\alpha \right)+2f_{21}\bar{\beta }+f_{22}\bar{\beta }\left(\bar{\alpha }{\text{e}}^{-i{\omega }_0{\tau }_0}+\alpha {\text{e}}^{i{\omega }_0{\tau }_0}\right)\\ +f_{23}\bar{\beta }\left(\bar{\alpha }+\alpha \right)+f_{24}\bar{\beta }\left(\alpha \bar{\alpha }{\text{e}}^{i{\omega }_0{\tau }_0}+\alpha \bar{\alpha }{\text{e}}^{-i{\omega }_0{\tau }_0}\right)],\end{array}$

$g_{02}=2\bar{D}{\tau }_0\left[f_{11}+f_{12}\bar{\alpha }+f_{21}\bar{\beta }{\text{e}}^{2i{\omega }_0{\tau }_0}+f_{22}\bar{\beta }\bar{\alpha }{\text{e}}^{i{\omega }_0{\tau }_0}+f_{23}\bar{\beta }\bar{\alpha }{\text{e}}^{2i{\omega }_0{\tau }_0}+f_{24}{\bar{\alpha }}^2\bar{\beta }{\text{e}}^{i{\omega }_0{\tau }_0}\right],$

$\begin{array}{c}{g}_{21}=2\bar{D}{\tau }_0[f_{11}\left(W_{20}^1\left(0\right)+2W_{11}^1\left(0\right)\right)+f_{12}\left(W_{11}^2\left(0\right)+\frac{1}{2}{W}_{20}^2\left(0\right)+\frac{1}{2}{W}_{20}^1\left(0\right)\bar{\alpha }+W_{11}^1\left(0\right)\alpha \right)\\ +\bar{\beta }\left(f_{21}\left(W_{20}^1\left(-1\right){\text{e}}^{i{\omega }_0{\tau }_0}+2W_{11}^1\left(0\right){\text{e}}^{-i{\omega }_0{\tau }_0}\right)\right)\\ +f_{22}\left(\frac{1}{2}{W}_{20}^2\left(0\right){\text{e}}^{i{\omega }_0{\tau }_0}+W_{11}^2\left(0\right){\text{e}}^{-i{\omega }_0{\tau }_0}+\frac{1}{2}{W}_{20}^1\left(-1\right)\bar{\alpha }+\alpha W_{11}^1\left(-1\right)\right)\\ +f_{23}\left(\frac{1}{2}{W}_{20}^2\left(-1\right){\text{e}}^{i{\omega }_0{\tau }_0}+W_{11}^2\left(-1\right){\text{e}}^{-i{\omega }_0{\tau }_0}+\frac{1}{2}{W}_{20}^1\left(-1\right)\bar{\alpha }{\text{e}}^{i{\omega }_0{\tau }_0}+W_{11}^1\left(-1\right)\alpha {\text{e}}^{-i{\omega }_0{\tau }_0}\right)\\ +f_{24}\left(\frac{1}{2}{W}_{20}^2\left(0\right)\bar{\alpha }{\text{e}}^{i{\omega }_0{\tau }_0}+W_{11}^2\left(0\right)\alpha {\text{e}}^{-i{\omega }_0{\tau }_0}+\alpha W_{11}^2\left(-1\right)+\frac{1}{2}\bar{\alpha }{W}_{20}^2\left(-1\right)\right)],\end{array}$

其中，

$f_{11}=\left(\frac{hb}{{\left(b+u_5\right)}^3}-a_1\right),f_{12}=-c_1\left(1-m\right),f_{21}=\frac{{\left(1-m\right)}^2{r}_2^2}{c_2\left(u_5\left(1-m\right)+k\right)},$

$f_{22}=\frac{r_2\left(1-m\right)}{u_5\left(1-m\right)+k},f_{23}=\frac{r_2\left(1-m\right)}{u_5\left(1-m\right)+k},f_{24}=-\frac{c_2}{u_5\left(1-m\right)+k}.$

显然， $g_{20},g_{11},g_{02},g_{21}$ 的表达式中存在未知的 $W_{20}\left(-1\right),W_{11}\left(-1\right),W_{20}\left(0\right),W_{11}\left(0\right)$。因此，进一步计算 $W_{20}\left(\theta \right),W_{11}\left(\theta \right)$ 的值。

由方程(2.3.2)与(2.3.3)可得

$\begin{array}{c}\stackrel{\dot{}}{W}={\stackrel{\dot{}}{U}}_t-2Re\left\{\stackrel{\dot{}}{z}q\right\}={\stackrel{\dot{}}{U}}_t-\stackrel{\dot{}}{z}q-\stackrel{\dot{}}{\bar{z}}\bar{q}=P{U}_t+Q{U}_t-\stackrel{\dot{}}{z}q-\stackrel{\dot{}}{\bar{z}}\bar{q}\\ =\{\begin{array}{l}PW-2Re\left\{{\bar{q}}^{*}\left(\theta \right)f\left(0\right)q\left(\theta \right)\right\},0<\theta \le 1\\ PW-2Re\left\{{\bar{q}}^{*}\left(0\right)f\left(0\right)q\left(0\right)\right\}+f\left(0\right),\theta =0\end{array}\\ =PW+H\left(z,\bar{z},\theta \right)\end{array}$

其中，

$H\left(z,\bar{z},\theta \right)=\frac{H_{20}\left(\theta \right)z^2}{2}+H_{11}\left(\theta \right)z\bar{z}+\frac{H_{02}\left(\theta \right){\bar{z}}^2}{2}+\cdots .$

由方程(2.3.4)与(2.3.5)可知

$\begin{array}{c}\stackrel{\dot{}}{W}\left(z,\bar{z}\right)=W_z\stackrel{\dot{}}{z}+W_{\stackrel{\bar{z}}{z}}\stackrel{\dot{}}{\bar{z}}=W_{20}\left(\theta \right)z\stackrel{\dot{}}{z}+W_{11}\left(\theta \right)\bar{z}\stackrel{\dot{}}{z}+W_{02}\bar{z}\stackrel{\dot{}}{\bar{z}}+W_{11}\left(\theta \right)z\stackrel{\dot{}}{\bar{z}}+O\left({\left|\left(z,\bar{z}\right)\right|}^3\right)\\ =W_{20}\left(\theta \right)z\left(i{\omega }_0{\tau }_{0}z+g\left(z,\bar{z}\right)\right)+W_{11}\left(\theta \right)\bar{z}\left(i{\omega }_0{\tau }_0\bar{z}+\bar{g}\left(z,\bar{z}\right)\right)\\ +W_{11}z\left(-i{\omega }_0{\tau }_0\bar{z}+\bar{g}\left(z,\bar{z}\right)\right)+W_{02}\left(\theta \right)\bar{z}\left(-i{\omega }_0{\tau }_0\bar{z}+\bar{g}\left(z,\bar{z}\right)\right)+O\left({\left|\left(z,\bar{z}\right)\right|}^3\right)\\ =i{\omega }_0{\tau }_0{W}_{20}\left(\theta \right)z^2-i{\omega }_0{\tau }_0{W}_{02}\left(\theta \right){\bar{z}}^2+O\left({\left|\left(z,\bar{z}\right)\right|}^3\right)\end{array}$

比较系数得

$\left(2i{\omega }_0{\tau }_{0}I-P\left(0\right)\right)W_{20}\left(\theta \right)=H_{20}\left(\theta \right),$

$P\left(0\right)W_{11}\left(\theta \right)=-H_{11}\left(\theta \right),$ (2.3.6)

$\left(2i{\omega }_0{\tau }_{0}I+P\left(0\right)\right)W_{02}\left(\theta \right)=-H_{02}(\; \theta \; )$

对于 $-1\le \theta <0$，有

$\begin{array}{c}H\left(z,\bar{z},\theta \right)=-2Re\left\{{\bar{q}}^{*}\left(\theta \right)Q\left(0\right)q\left(\theta \right)\right\}=-g\left(z,\bar{z}\right)q\left(\theta \right)-\bar{g}\left(z,\bar{z}\right)\bar{q}\left(\theta \right)\\ =-\left(g_{20}\frac{z^2}{2}+g_{11}z\bar{z}+g_{02}\frac{{\bar{z}}^2}{2}+\cdots \right)q\left(\theta \right)-\left({\bar{g}}_{20}\frac{{\bar{z}}^2}{2}+{\bar{g}}_{11}z\bar{z}+{\bar{g}}_{02}\frac{{\bar{z}}^2}{2}+\cdots \right)\bar{q}\left(\theta \right).\end{array}$

从而得到

$H_{20}\left(\theta \right)=-g_{20}q\left(\theta \right)-{\bar{g}}_{02}\bar{q}\left(\theta \right),$

$H_{11}\left(\theta \right)=-g_{11}q\left(\theta \right)-{\bar{g}}_{11}\bar{q}\left(\theta \right).$ (2.3.7)

结合方程(2.3.6)、方程(2.3.7)以及 $P\left(0\right)$ 的定义知

$\dot{W_{20}}\left(\theta \right)=2i{\omega }_0{\tau }_0{W}_{20}\left(\theta \right)+g_{20}q\left(\theta \right)+{\bar{g}}_{02}\bar{q}\left(\theta \right),$

从而解得

$W_{20}\left(\theta \right)=\frac{i{g}_{20}q\left(0\right)}{{\omega }_0{\tau }_0}{\text{e}}^{i{\omega }_0{\tau }_0\theta }+\frac{i{\bar{g}}_{02}\bar{q}\left(0\right)}{3{\omega }_0{\tau }_0}{\text{e}}^{-i{\omega }_0{\tau }_0\theta }+G_1{\text{e}}^{2i{\omega }_0{\tau }_0\theta },$

$W_{11}\left(\theta \right)=\frac{-i{g}_{11}q\left(0\right)}{{\omega }_0{\tau }_0}{\text{e}}^{i{\omega }_0{\tau }_0\theta }+\frac{i{\bar{g}}_{11}\bar{q}\left(0\right)}{{\omega }_0{\tau }_0}{\text{e}}^{-i{\omega }_0{\tau }_0\theta }+G_2.$

其中， $G_1,G_2$ 为二维常数向量。

当 $\theta =0$ 时，有

$H_{20}\left(0\right)=-g_{20}q\left(0\right)-{\bar{g}}_{02}\bar{q}\left(0\right)+{\tau }_0{\left(z_1,z_2,0\right)}^{\text{T}},$

$H_{11}\left(0\right)=-g_{11}q\left(0\right)-{\bar{g}}_{11}\bar{q}\left(0\right)+{\tau }_0{\left(z_3,z_4,0\right)}^{\text{T}}.$

其中，

$z_1=f_{11}+f_{12}\alpha ,$

$z_2=f_{21}{\text{e}}^{-2i{\omega }_0{\tau }_0}+f_{22}{\text{e}}^{-i{\omega }_0{\tau }_0}\alpha +f_{23}\alpha {\text{e}}^{-2i{\omega }_0{\tau }_0}+f_{24}{\alpha }^2{\text{e}}^{-i{\omega }_0{\tau }_0},$

$z_3=2f_{11}+f_{12}\left(\alpha +\bar{\alpha }\right),$

$z_4=2f_{21}+f_{22}\left({\text{e}}^{-i{\omega }_0{\tau }_0}\bar{\alpha }+{\text{e}}^{i{\omega }_0{\tau }_0}\alpha \right)+f_{23}\left(\alpha +\bar{\alpha }\right)+f_{24}\left(\alpha \bar{\alpha }{\text{e}}^{-i{\omega }_0{\tau }_0}+\alpha \bar{\alpha }{\text{e}}^{i{\omega }_0{\tau }_0}\right).$

由P(0)的定义以及方程(2.3.6)可得

${\displaystyle {\int }_{-1}^0\text{d}\eta }\left(\theta \right)W_{20}\left(\theta \right)=2i{\omega }_0{\tau }_0{W}_{20}\left(0\right)-H_{20}\left(0\right),{\displaystyle {\int }_{-1}^0\text{d}\eta }\left(\theta \right)W_{11}\left(\theta \right)=-H_{11}\left(0\right).$

根据

$H_{20}\left(0\right)=2i{\omega }_0{\tau }_0{W}_{20}\left(0\right)-{\tau }_0{B}_1{W}_{20}\left(0\right)-{\tau }_0{B}_2{W}_{20}\left(-1\right),$

$H_{11}\left(0\right)=-{\tau }_0{B}_1{W}_{11}\left(0\right)-{\tau }_0{B}_2{W}_{11}\left(-1\right).$

解得

$\begin{array}{c}{G}_1=\frac{1}{2i{\omega }_0{\tau }_{0}I-{\tau }_0{B}_1-{\tau }_0{B}_2{\text{e}}^{-2i{\omega }_0{\tau }_0}}(H_{20}\left(0\right)+2g_{20}q\left(0\right)+\frac{2}{3}{\bar{g}}_{02}\bar{q}\left(0\right)+\frac{B_{1}i{g}_{20}q\left(0\right)}{{\omega }_0}\\ +\frac{B_{1}i{\bar{g}}_{02}\bar{q}\left(0\right)}{3{\omega }_0}+B_2\frac{i{g}_{20}q\left(0\right)}{{\omega }_0}{\text{e}}^{-i{\omega }_0{\tau }_0}+B_2\frac{i{\bar{g}}_{02}\bar{q}\left(0\right)}{3{\omega }_0}{\text{e}}^{i{\omega }_0{\tau }_0}),\end{array}$

$G_2=\frac{1}{{\tau }_0\left(B_1+B_2\right)}\left(-H_{11}\left(0\right)+\frac{B_{1}i{g}_{11}q\left(0\right)}{{\omega }_0}-\frac{B_{1}i{\bar{g}}_{11}\bar{q}\left(0\right)}{{\omega }_0}+\frac{B_{2}i{g}_{11}q\left(0\right)}{{\omega }_0}{\text{e}}^{-i{\omega }_0{\tau }_0}-\frac{B_{2}i{\bar{g}}_{11}\bar{q}\left(0\right)}{{\omega }_0}{\text{e}}^{i{\omega }_0{\tau }_0}\right).$

从而得到下列参数表达式：

$c_1\left(0\right)=\frac{i}{2{\omega }_0{\tau }_0}\left(g_{20}{g}_{11}-2{\left|g_{11}\right|}^2-\frac{{\left|g_{02}\right|}^2}{3}\right)+\frac{g_{21}}{2},$

${\beta }_2=Re\left(c_1\left(0\right)\right),{\mu }_2=-\frac{Re\left(c_1\left(0\right)\right)}{Re\left({\lambda }^{\prime }\left({\tau }_0\right)\right)},$

$T_2=-\frac{Im\left\{c_1\left(0\right)\right\}+{\mu }_{2}Im\left\{{\lambda }^{\prime }\left({\tau }_0\right)\right\}}{{\omega }_0{\tau }_0}.$

根据 $c_1\left(0\right),{\beta }_2,{\mu }_2,T_2$ 这些参数值，可以得到时滞参数临界值处的分岔方向和周期解稳定性。 ${\mu }_2>0\left(<0\right)$ 时对应超临界Hopf分岔(亚临界)； ${\beta }_2<0\left(>0\right)$ 时对应稳定的周期解(不稳定的)； $T_2>0\left(<0\right)$ 时，对应周期解的周期是增加的(减少)。

3. 数值模拟

本节利用数值模拟研究时滞、Allee效应以及食饵避难对模型动力学性质的影响。给定部分参数取值如下：

$r_1=0.6,r_2=0.3,c_1=0.1,c_2=0.1,k=0.1,a_1=0.01,b=\mathrm{0.7.}$

此时，时滞参数的临界值和正平衡点为分别为 ${\tau }_0=1.7529$， $E_5=\left(6.0051,9.3076\right)$。

在第2节的分析表明时滞会导致平衡点 $E_5$ 失稳，其对应的数值模拟结果分别如图1和图2所示。由图1和图2可以看出当时滞参数小于临界值时( $\tau =1.5<{\tau }_0$ )，平衡点 $E_5$ 是稳定的；当时滞参数大于临界值时( $\tau =1.9>{\tau }_0$ )， $E_5$ 不稳定且模型中存在稳定的极限环。

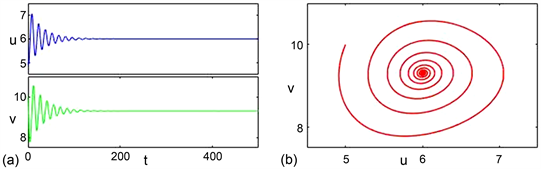
Figure 1. $m=0.5,h=0.5,\tau =1.5$. (a) Time series; (b) Phase portrait

图1. $m=0.5,h=0.5,\tau =1.5$。(a) 时序图；(b) 相图

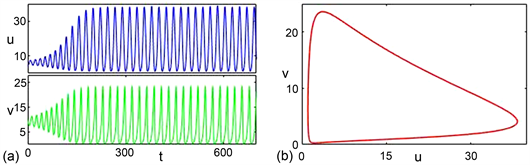
Figure 2. $m=0.5,h=0.5,\tau =1.9$. (a) Time series; (b) Phase portrait

图2. $m=0.5,h=0.5,\tau =1.9$。(a) 时序图；(b) 相图

图3表明，平衡点 $E_5$ 的稳定性关于时滞参数 $\tau$ 值的变化是敏感的。由图可以看出，当时滞参数低于临界值时，正平衡点是稳定的；当时滞参数超过临界值时，正平衡点失去稳定性，并且 $\tau$ 值的增大会增强种群密度振荡的幅度。

此外，为了进一步讨论Allee效应常数h和食饵避难项m对模型(1.2)的影响，分别对模型(1.2)关于参数h和m进行了敏感性分析。从图4中可以看出，捕食者种群密度对参数h和m的变化是敏感的。图4(a)中随着参数h值增大时，平衡点由不稳定的状态转为稳定的状态，即参数h值越大越有利于平衡点的稳定。而图4(b)显示，较大或较小参数m值有利于平衡点的稳定，处于中间范围的参数m值会导致种群密度的振荡。当参数m的值逐渐增大，稳定的平衡点由Hopf分岔变得不稳定，随着m值继续增大，平衡点再次经历Hopf分岔最终变为稳定。

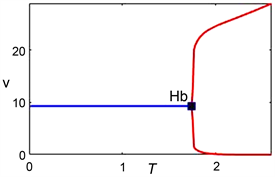
Figure 3. Analysis of sensitivity with $m=0.5,h=0.5$. The solid blue line denotes the stable equilibrium; the solid red line represents the maximal and minimal density of predator population. The point “Hb” is the Hopf bifurcation point

图3. 敏感性分析： $m=0.5,h=0.5$。蓝线为稳定平衡点，红线表示捕食者种群最大和最小密度，“Hb”为Hopf分岔点

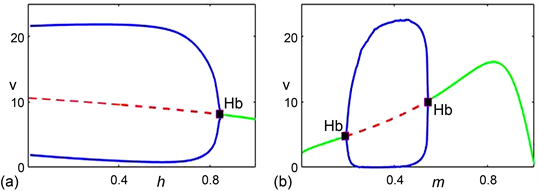
Figure 4. (a) Analysis of sensitivity with $m=0.5,\tau =1.8$ ; (b) Analysis of sensitivity with $h=0.5,\tau =1.8$. The solid green line denotes the stable equilibrium; the dashed red line indicates the positive equilibrium which is unstable. The solid blue lines represent the maximal and minimal density of predator populations. The point “Hb” is the Hopf bifurcation point

图4. (a) 敏感性分析： $m=0.5,\tau =1.8$ ；(b) 敏感性分析： $h=0.5,\tau =1.8$。其中绿线为稳定平衡点，红色虚线表示平衡点是不稳定的，蓝线表示捕食者种群的最大和最小密度，“Hb”为Hopf分岔点

4. 结论

本文建立了一类带有时滞的修正的Leslie-Gower捕食模型，旨在研究时滞效应对模型动力学性质的影响。首先，给出了模型(1.2)中正平衡点的存在性与稳定性分析。其次，证明了模型(1.2)在正平衡点处经历Hopf分岔，进而产生周期解，并进一步计算了Hopf分岔的方向以及周期解的稳定性。最后，利用数值模拟揭示了时滞使正平衡点发生失稳，并且时滞参数的增大会加剧种群密度的振荡幅度。此外，敏感性分析显示，种群的密度变化与平衡点的稳定性对Allee效应参数和食饵避难参数的变化具有一定的敏感性。因此，本文结果表明时滞、Allee效应以及食饵避难的共同作用使模型的动力学性质更加复杂。

致谢

首先，感谢我的导师——赵敏老师为我们营造了良好的学术氛围；在生活上关心我们，在科研上严格要求我们，让我们习得了良好的生活习惯和严谨的科研精神。其次，感谢我的师兄们，尤其是戴传军老师和郭庆博士一直给予我科研工作上莫大的帮助与坚持下去的信念。让我度过了一段紧张且充实，快乐而难忘的科研生活。感谢学校以及学校的各位老师们，谆谆教诲，终身难忘！最后，非常感谢百忙之中抽出时间审阅本论文的各位老师们！