1. 引言
随着网络技术的快速发展,数字图像数据成为日常生活中交流信息的主要载体,经由网络在人群中传播共享。在公众重视信息安全和个人隐私的背景下,数字图像的保密需求也日益突出,减少图像数据受到非法复制、传播等有害行为的影响,保证图像在传输过程中的安全性和保密性具有重要的意义。图像数据本身具有信息量巨大、数据冗余度高、相邻像素高度相关性等固有特性,图像数据在通信中需要很强的实时性,因此需要速度快、安全性高的加密方法。这些特点使得针对文本数据设计的传统加密系统DES、AES已经不适用于图像加密 [1]。因此有必要为图像的加密设计更有针对性的加密方法。许多学者对此作了诸多的研究,提出了许多有效算法,其中基于混沌理论的图像加密算法是被最广泛采用的方法之一。混沌现象是在非线性动力系统中出现的确定、伪随机的现象。混沌系统具有极强的初值和参数敏感性,生成的序列具有很强的伪随机性、遍历性和可重复生成等优良性质,这些属性与密码学的混淆与扩散等性质有着天然的高度相似性,因此混沌系统具有设计性能良好的图像加密系统的巨大潜力 [2] [3]。
基于混沌理论的图像加密系统一般由置换与扩散两个过程构成。置乱过程通过混沌系统的遍历性与随机性将图像的像素灰度值重新排列,破坏图像灰度值对位置的高度相关性,有效地从视觉上破坏图像像素原本的位置信息。扩散过程利用混沌系统对初始值与系统参数高度敏感等特点,设计具有优良扩散效应的扩散函数,使得任何一个像素的亮度值的改变,可以对这个像素后面的像素产生骨牌多米诺效应的效果。基于混沌系统的图像加密算法的像素置乱可以采用各种各样的变换实现,如Arnold变换,Standard变换等 [3] [4]。这些经典的变换置乱形式相对简单,单一的应用会被轻易通过选择明文、已知明文等密码分析后破解 [5] [6] [7]。为了提高加密算法抵御被黑客破解的能力,本文通过将经典的成熟混沌系统斜帐篷映射、Arnold映射组成混合的系统,设计一种新的彩色图像加密算法。混沌系统的混合应用,可以扩大密码空间的大小,增强加密系统抵御蛮力攻击的性能。另一方面,通过使用明文图像信息相关的敏感特征量来修正Arnold映射和斜帐篷映射的参数和初值,使得加密算法对明文图像的信息具有更好的敏感性,实现一次一密的加密效果。研究表明简单仅仅通过像素位置的置乱算法是脆弱的,很容易被黑客破解 [7] [8]。
灰度图像的亮度值的高比特位占据图像的主要信息,彩色图像三颜色通道的分量值的高比特位也是颜色的主要贡献部分 [9] [10]。图像相邻像素间,三颜色R、G、B分量之间均具有很强的相关性,所以设计加密算法的时候,应该考虑通过像素层次和比特层次间的置乱,达到破坏这种彩色图像的像素间和颜色分量间的强相关性。因此本文首先通过将三颜色分量的高2位比特值重组成6比特值,其他低比特值保留不变,从而可以将8比特的彩色图像重构成4个6比特的灰度图像。然后通过使用计算明文图像的信息不变量,修改斜帐篷映射的参数和初始值,使得斜帐篷映射生成的密钥流与明文高度相关。通过量化斜帐篷映射迭代生成的序列值,得到广义的离散Arnold变换的参数,并用离散Arnold变换对比特重构后的4个矩阵进行像素置乱。为了提高效率,置乱在高比特位矩阵与3个低比特位矩阵之间进行,通过斜帐篷映射的混沌序列具有均匀分布的特性,生成一个均匀分布的三值序列,来操控高比特矩阵与3个低比特矩阵之间的像素交换。通过上述比特重构和像素置乱后,达到了破坏像素值和像素位置的目的。为了进一步提高加密算法的性能和安全性,算法中还安排了一个像素层次的扩散过程,通过引入广义实数参数的Arnold变换用于生成扩散过程的密钥流。加密算法采用按位比特异或和加法模运算相结合的模式,既保证了扩散过程的可逆性也使得安全性能更好。结果表明,本文所设计的加密算法具有很好的安全性和加密性能,可以抵御蛮力攻击、统计分析攻击,差分分析攻击、选择明文和已知明文攻击等。
2. 相关知识
2.1. 斜帐篷混沌映射
斜帐篷混沌映射为分段的线性映射,广泛应用于混沌加密系统中,具体定义如(1)所示:
(1)
其中
,
是控制参数,控制着斜帐篷混沌映射的动力学特性。对于任意一个
,系统(1)的Lyapunov特征指数为
,说明该映射为混沌映射,该映射具有良好的动力学特性,生成的序列具有很好的伪随机性,分布均匀,高度依赖于初值和参数,可以用来生成加密算法的密钥流,
作为密钥。
2.2. 广义Arnold混沌映射
广义Arnold映射可以被用于置乱大小为
的图像的像素位置,其矩阵表示形式如(2):
(2)
其中
是原始像素的位置,
是置乱之后像素的位置,a和b是整数,在
中
取值。对于映射(2),容易计算得其最大Lyapunov特征指数为
,说明该映射是
混沌的 [3]。
本文将使用参数是整数和实数两种类型的广义Arnold映射。扩展(2)的整数a,b为实数,映射修改为公式(3),其中的状态变量取值在
中。这样的实参数广义Arnold映射将可以产生具有优良混沌特性的序列,其中的初值和系统参数的选择范围大大扩大,从而密钥空间也得到扩大。系统所生成的两组混沌序列,将用于扩散过程的加密。
(3)
3. 加密方案
本节提出了一种新的图像加密算法,并对其在信息安全中的应用进行了验证。加密算法中所使用的7个参数
作为密钥。加密算法的主要框架如图1所示。

Figure 1. The main frame of encryption algorithm
图1. 加密方案的主要框架
3.1. 置换操作
3.1.1. 扩张–收缩策略
文献 [9] 通过使用比特级置换代替传统的像素级置换,混淆效果得到了改善。但是该方法并没有在不同位平面之间置换,因此不能平滑不同位平面的波动分布,而是保持每个位平面的统计信息不变。文献 [10] 揭示了数字图像中比特分布的内在特征。像素的高位代表图像信息的高权重,高位平面之间有很强的相关性。统计表明,第8位平面和第7位平面的值趋于相反 [10]。在安全的密码系统中,这些特性不应被忽视。针对上述问题,文献提出一种扩张–收缩的策略,用一种新型的置换方式巧妙地同时进行位平面内和位平面间的置换,从而解决了上述的问题,有利于实现三个目标:1) 比特在彩色图像的三维矩阵中的整体分布应均匀;2)每个位平面内的比特分布应均匀;3) 相邻位平面之间的相关性应尽可能低。
为了描述方便,考虑一个大小为
的彩色图像,将原图像看作一个大小为
的三维矩阵P,P的元素值记录了原始明文图像的颜色分量值,即原图像位于像素
的R、G、B分量值
。读取彩色图像后,即可以得到图像的R、G、B分量所对应的二维矩阵。
在扩张策略中,R、G、B通道中每个像素的最高两个比特被分离出来组成一个新的6比特数值,其中最高的两位来自B通道,其次两位来自G通道,最低的两位来自R通道。各颜色通道中每个像素余下的6位比特保持不变,那么将会得到4个
的6比特像素平面。将这4个平面按顺时针次序依次放置在
矩阵的四个分块中,得到扩张矩阵M。扩张收缩策略如图2所示。随后对扩张矩阵M进行置乱与扩散,加密完成后按扩张的逆过程进行收缩得到原图像。
3.1.2. 置乱过程
在这一阶段,通过斜帐篷映射产生混沌序列,将该序列的值量化之后作为Arnold映射的参数,通过改变扩张后的矩阵M中的像素位置来对图像进行置乱处理。
首先,利用斜帐篷映射(1)生成混沌序列
,舍去前面的s个值,s为矩阵M中元素的总和:
,从而使得混沌序列
与明文图像P相关,可以很好的抵御差分攻击。
然后,利用
对区域I中的像素进行置乱,将其像素信息均匀分布至低位比特所组成的像素平面(II, III, IV)中。为此,利用
量化生成随机整数序列
,使得
。
的定义如式(4)所示:
(4)
将
重塑为
的矩阵S,根据
的取值判断区域I中对应位置的像素与II, III, IV中的哪个区域的像素进行交换。交换的位置由广义Arnold混沌映射(5)生成:
(5)
其中参数
由斜帐篷映射的值决定:
用三维坐标
表示像素在矩阵M中的位置,其中
表示像素所处的区域,
表示像素在所处区域的位置,则上述置乱过程可表示为交换关系(6):
(6)
经过一轮的置乱操作,高位比特所处的平面(第I区域)的像素被均匀分布到区域II, III, IV中去,使得相邻比特平面之间的相关性尽可能低。
3.2. 扩散操作
3.2.1. 一次扩散
Step 1. 将置乱后的扩张矩阵M按照左右均分为两个大小为
的矩阵
,然后将这两个矩阵组合得到一个大小与
矩阵一致的12比特矩阵C,其中矩阵C中数据的奇数比特位与对应位置的矩阵A的比特保持一致,偶数比特位与对应位置的矩阵B的比特保持一致。
Step 2. 用2.2节的广义Arnold映射式(3)进行迭代得到两个长度为
的混沌序列,其中
作为密钥。然后去掉该序列的前50位消除暂态影响,得到序列
,
,对这两个序列作如式(7)的处理,得到12比特序列
,
。
(7)
Step 3. 提取
的奇数比特位与
的偶数比特位组成一个新的12比特序列
,其中序列
中数字的奇数比特位与
的奇数比特位一致,
中数字的偶数比特位与
的偶数比特位一致,之后将序列
重塑为一个
的矩阵T。
Step 4. 对矩阵C和矩阵T进行异或运算(8),得到一次扩散矩阵
:
(8)
3.2.2. 二次扩散
Step 1. 对
进行进一步的扩散。首先将
按行拉直为
的向量
,将
按式(9)进行扩散操作得到二次扩散密文向量
。
(9)
Step 2. 将
重塑为
大小的密文矩阵
。
Step 3. 对
的比特进行拆分。再次将
分为两个6比特矩阵
,比特矩阵
由
的前6比特位组成,比特矩阵
由
的后6比特位组成,最后将
按收缩策略重新合并为最终的加密矩阵
,得到最后的彩色密文图像。
4. 仿真结果和安全性分析
为了说明所提出的加密方案的安全性,给出了实验结果和安全性分析。所有模拟均在2.80GHz CPU,8GB内存的计算机上运行,编译平台为MATLAB R2017a。
4.1. 初值选取
读取大小
为彩色明文图像I,并求出I的颜色分量值总和k,对k进行如式(10)的变换得到
。
(10)
构造一个初值
,控制系数
的斜帐篷映射,生成长度为
的序列,然后丢掉前
项,得到一个长度为7的序列
,对这个序列内的各个数字作如下处理得到加密所需要的各个密钥值。
,
,
,
,
,
,
.
各个密钥的具体说明如表1所示。相较于直接对密钥进行赋值,该做法将明文与混沌序列相关联,组合成密钥,可以增强明文敏感性,同时明文与密钥生成相关,可以实现一图一密的效果。在实际加密中,所有这些参数,即 ,均可以作为密钥使用。
,均可以作为密钥使用。
4.2. 仿真结果
在本节中,我们选择大小为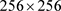 的Lenna彩色图像作为测试图像进行加密和解密实验。产生的实验的视觉效果如图3所示。结果表明,加密图像是类噪声图像,算法还可以有效地应用于各种形式的图像,如灰度图像、彩色图像和二值图像。
的Lenna彩色图像作为测试图像进行加密和解密实验。产生的实验的视觉效果如图3所示。结果表明,加密图像是类噪声图像,算法还可以有效地应用于各种形式的图像,如灰度图像、彩色图像和二值图像。
 (a) 原图像
(a) 原图像  (b) 加密图像
(b) 加密图像
Figure 3. The encryption results
图3. Lena图像的加密结果
4.3. 密钥空间分析
密钥空间是所有可行密钥构成的集合。所提出的加密算法的密钥是双精度数字。为了更好的安全性能,加密算法应该对其安全密钥的任何变化都非常敏感,并拥有大于2100的空间,足以承受强力的穷举攻击。本文构建的加密方案有7个密钥: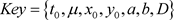 。如果实数计算精度为10−14,我们可以计算得到总的密钥空间为
。如果实数计算精度为10−14,我们可以计算得到总的密钥空间为 ,根据 [11] 中的建议,密钥空间至少为2100,故此加密算法有足够大的密钥空间,可有效的抵御穷举攻击与暴力破解。
,根据 [11] 中的建议,密钥空间至少为2100,故此加密算法有足够大的密钥空间,可有效的抵御穷举攻击与暴力破解。
4.4. 密钥敏感性分析
一个好的加密系统应该对密钥和明文图像的细微变化非常敏感。灵敏度可通过NPCR (像素数变化率)和UACI(统一平均变化强度)进行定量评价,NPCR和UACI的值越接近其数学期望值NPCR = 99.6094%,UACI = 33.4635%,加密性能越好,说明密文对密钥的变化越敏感 [12]。NPCR和UACI的计算式如(11)~(12)所示。
 (11)
(11)
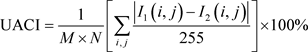 (12)
(12)
其中 和
和 是对应于两个微小差别的密钥所对应的加密图像。在实验中面对图像在加密过程中做微小调整,对密钥中的各个值进行微小的变化
是对应于两个微小差别的密钥所对应的加密图像。在实验中面对图像在加密过程中做微小调整,对密钥中的各个值进行微小的变化 ,对进行检验的密钥分别采取
,对进行检验的密钥分别采取 和
和 的变化,分别计算两次变化的NPCR与UACI值,求得两次变化的平均值如表2所示。从表2可以看出,所提出的图像加密算法对密钥均非常敏感。
的变化,分别计算两次变化的NPCR与UACI值,求得两次变化的平均值如表2所示。从表2可以看出,所提出的图像加密算法对密钥均非常敏感。

Table 2. The results of key sensitivity (%)
表2. 密钥敏感性的结果(%)
4.5. 统计分析
为了证明所提出的加密方案的安全性,我们进行了以下统计测试。
直方图分析。图像直方图可以较为直观的看出图像的灰度值分布情况,如果密文的灰度值频率直方图分布越均匀,表明加密效果越好,从加密图像中推断原图像信息越是困难。在经过置乱与扩散后,图像的R、G、B三个分量的灰度值发生了变化,对原图像和加密图像的灰度值进行直方图统计,结果如图4所示。由图4可知密文图像的R、G、B分量值的直方图发生了显著变化,直方图变得平坦,表明256个灰度级所对应的像素点个数相对平均,从直方图分析角度来看,加密效果好。
相关性分析。相邻像素相关性反映图像相邻位置像素值的相关程度。良好的图像加密算法能有效降低相邻像素的相关性。在实验中,我们从原始图像和加密图像中随机选取6000对相邻像素,并在水平、垂直和对角线方向上分析相关性。相关系数由式(13)计算。
 (13)
(13)
式中, 和
和 表示某对相邻像素的像素值。协方差与方差的计算公式如下:
表示某对相邻像素的像素值。协方差与方差的计算公式如下:
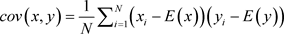 ,
,
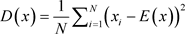 ,
, 。
。

Table 3. The correlation coefficients of adjacent pixels
表3. 相邻像素之间的相关性系数
结果如表3所示,结果显示明文图像的相邻像素相关性极强,密文图像的相邻像素相关性极弱,加密算法可以很好地削弱相邻像素的相关性。为更加直观展示结果,每种方向的相关性分布如图5所示:
从图5中可以看出明文中垂直、水平、对角线三个方向的像素点都集中在对角线方向上,表明像素之间的相关性较强。而密文中三个方向的像素点较均匀地布满整个平面,表明密文的像素之间的相关性很弱,近乎随机。
4.6. 信息熵分析
图像的信息熵是一种度量随机特征的统计形式,能测试不确定性,能反映出图像中平均信息的多少。当图像中信息量越大时熵的值越大,图像越粗糙,当图像中信息量越小是熵的值越小,图像越平滑。由于灰度值的范围是[0, 255],灰度级总数记为L = 256,所以熵的取值范围为[0, 8]。信息熵的计算公式如(14)。
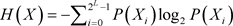 (14)
(14)
式中 表明信息
表明信息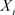 出现的频率。按式(14)计算,加密后的图像信息熵为7.9973,很接近于最大值8,表明图像中的信息不确定度很大,能被攻击的可能性很小,很难泄露信息。
出现的频率。按式(14)计算,加密后的图像信息熵为7.9973,很接近于最大值8,表明图像中的信息不确定度很大,能被攻击的可能性很小,很难泄露信息。
4.7. 明文敏感性分析
图像加密算法的差分攻击分析是研究在相同密钥下密文图像会在多大程度上受明文图像的影响,攻击者通常通过选择明文分析或选择密文分析来实现差分攻击。为了分析加密算法抵御差分攻击的能力,很有必要分析明文敏感性,分析中有两个特征量可以很好地刻画该项性能,即是公式(11),(12)所计算的NPCR和UACI,只不过这里改变量是明文,对明文实施最微小的变化,用同样的密钥加密,得到两幅密文图像并计算这两个值,如果很接近数学期望值NPCR = 99.6094%,UACI = 33.4635%,则表明算法抵御差分攻击的能力越强。本文随机选取像素图像中的100个像素,在每一次改变中对其中一个像素的值增加1,将变更后加密的图像与原加密图像进行对比,计算两副密文图像的UACI及NPCR。经过100次的试验后得到NPCR和UACI的平均值分别为99.62%和33.50%。结果表明本文的图像加密算法对明文的微小差异非常敏感,可以有效抵御差分分析的攻击。
5. 总结
本文设计了一种新的基于混沌和位平面交换的彩色图像加密算法。将彩色明文图像三颜色分量中权重大的第7~8比特位平面进行重构,结合广义Arnold映射来进行重构后的位平面之间的交换置乱,将三颜色分量的高位平面的信息均匀分散到低位平面,有效削弱了相邻像素和颜色分量间的相关性。算法还应用实参数的广义Arnold映射生成混沌序列,对置乱图像进行一种高效率的扩散,进一步提升了算法的安全性和性能。实验和安全分析表明,该加密算法具有较高的安全性和较好的加密性能,满足图像加密的需求。
基金项目
论文研究资助项目为广东省大学生创新创业项目以及国家自然科学基金项目(No. 11771265);广东省普通高校重点研究项目(No. 2019KZDXM034);广东省基础与应用基础研究基金项目(No. 2020B1515310018)。
NOTES
*通讯作者。