1. 引言
探地雷达作为一种常用的地球物理检测方法,具有无损、快速、连续成像的特点,广泛应用于各种工程检测 [1]。目前广泛使用的探地雷达都属于冲激脉冲体制,即雷达发射一个高频宽带的时域脉冲,通过接收到反射信号的时间、幅度、相位等信息推断地下介质结构。这种体制探地雷达为了提高距离分辨率一般采用短的发射脉冲,但由于受到发射功率的限制导致作用距离不远 [2],分辨率也受限于脉冲宽度,实际应用中探测深度和分辨率方面很难进一步提升。
步进频率调制连续波(Stepped-frequency Continuous. SFCW)体制探地雷达作为频域探地雷达的一种,近些年逐渐成为该领域研究热点.。不少学者或机构相继研发出了SFCW体制探地雷达系统,其相比于冲激脉冲体制探地雷达在探测性能上的优越性也在实际使用中得到体现。陶春康等 [3] 设计了一种步进扫频的宽带探地雷达前端,用该系统分别发射151个及51个步进频率脉冲,对接收到的地下物体反射的回波信号进行混频和滤波,经实验测试分辨率分别能达到5 cm和15 cm,证明SFCW探地雷达可以通过选取不同的步进频点数来达到不同的分辨率。许泽善等 [4] 将三维SFCW探地雷达应用于道路沥青厚度检测,达到超高的浅层分辨率。Tronca等 [5] 运用带宽范围在0.2~4 GHz的SFCW探地雷达和GSSI公司的中心频率为2.7 Hz的脉冲探地雷达在三种实验条件下进行了实测效果对比,结果表明SFCW探地雷达在达到较大探测深度的同时能保证较高的分辨率。Hamran等 [6] 对比研究了其机构研发的SFCW探地雷达和商用脉冲探地雷达的动态范围,证明其研发的SFCW系统动态范围比脉冲系统高40 dB,实际动态范围超过200 dB,而动态范围则影响到GPR的最大作用距离。Pieraccini等 [7] 在Hamran等的基础上,将其在对比系统动态范围时的假设条件设置的更具适用性,在15种实验条件下对两种体制探地雷达进行实测效果对比,SFCW探地雷达的结果比脉冲雷达能提供更多深部反射信号,受噪声影响更小。
对SFCW探地雷达进行数值模拟研究,对其在实际使用中采集数据的解释具有指导意义。目前针对SFCW探地雷达数值模拟效率提升的研究工作进行较少。Kafedziski等 [8] 对频带范围在1.01~2 GHz的含100个频点的SFCW探地雷达进行正演模拟,实现对均匀半空间下单一异常体的检测,但其是在每个频点逐次进行正演,虽然模型设置较小,但耗时仍然较长。SFCW探地雷达数值模拟计算量按频点数成倍增加,是进行其正演模拟时首先要解决的问题。探地雷达数值模拟方法中,时域有限差分法(FDTD)具有直接时域计算、思路清晰、编程简单等特点,是计算电磁学中最流行的方法 [9]。FDTD以电、磁场分量在时间空间上交错采样计算方法来模拟电磁波场 [10],广大学者对应用FDTD方法进行电磁波场的正演计算问题进行了研究并将其运用到探地雷达的正演模拟中 [11]。基于FDTD理论,相关学者对求解探地雷达正演问题也进行了程序编写 [12],并给出了所有源代码。其中开源程序gprMax能够实行并行计算及利用CUDA对FDTD算法进行加速,效率较高 [13],是进行探地雷达FDTD数值模拟时的优选程序。相关学者用gprMax针对实际问题进行探地雷达正演模拟,并取得了较好的效果 [14]。
综上,目前对于SFCW探底雷达的研究主要在硬件及应用方面,在数值模拟方面尚欠缺成熟高效的方法。本文给出了SFCW探地雷达正演模拟及数据处理的详细方法,在gprMax程序的基础上,结合模型的冲激响应,来解决SFCW正演模拟时计算量过大的问题,并在数值模拟基础上进行与脉冲探地雷达抗噪性能的对比研究。
2. 原理
2.1. SFCW探地雷达基本原理
常规脉冲探地雷达发射和接收的为高频宽带的脉冲信号,而SFCW探地雷达每次发射和接收的信号为单频的连续波信号,其频率变化可表示为:
(1)
其中,f0为起始频率,fn为第n个频率,Δf为频率步长,带宽
。
发射信号形式(连续正弦波)可表示为:
(2)
其中n为第n个频点。
假设信号在均匀介质中传播的速度为v,一个距离为d的目标反射回波信号可表示为:
[15] (3)
其中,An为回波幅度值,
为电磁波双程走时。
其中,第n个频率的相位变化为:
(4)
则接收到的反射回波信号可表示为:
(5)
这样目标体距离就转化为不同频点连续波对应的相移,对于频率
,对应有
,幅度
。对于序列
,
,可通过逆傅里叶变换转换到时域内进行信号融合。
2.2. gprMax正演及LTI系统的冲激响应
gprMax是用python语言编写的探地雷达FDTD正演软件,可用来进行多种电磁问题的数值模拟。其操作采用命令行窗口的形式,需要编写规定格式的模型文件(.in文件),在模型文件中定义介质的空间分布和电性参数(相对介电常数εr,电导率σ,相对磁导率μr,磁损耗σr),给出激励源的类型和位置等参数,将模型文件路径输入到gprMax命令行窗口中,即可调用程序进行计算,输出文件为若干道雷达反射数据(.out文件)。利用gprMax进行正演模拟时,首先要对正演模型进行空间离散和时间离散。
网格步长需要小于模型介质中最小波长的十分之一,即:
(6)
其中,dx、dy、dz分别为模型x、y、z三个方向上的网格步长,fmax为源信号最高频率,εmax为模型中介质的最大相对介电常数。
对于脉冲信号(如Ricker子波),信号的最高频率fmax约为信号中心频率的2到3倍。
对于步进频率信号,fmax = fn,fn为步进终止频率。
控制了网格步长后,为了满足有限差分收敛条件,时间步长由以下条件控制:
(7)
模型边界采用PML (完全匹配层)吸收边界,完成模型创建后,即可读入模型文件后进行正演,正演结果得到若干道Ascan,可合成Bscan读入Matlab进行相关处理。
由于为了满足公式(6)和公式(7)控制条件,网格步长需要剖分得很小,时间步长也很小,意味着每道Ascan要进行更多次迭代计算,也这样就导致模型正演模拟占用时间较长。尤其是对于步进频率信号而言,含有n个频率的信号,意味着需要进行n次正演计算,这将导致正演计算的时间成倍增加。尽管gprMax可利用CUDA进行加速,但计算量成倍的增加,需要从算法方面研究提升正演效率的方法。
由于正演采用的时域有限差分法满足线性时不变系统(LTI)的特性,而线性时不变系统对任意一个输入信号的响应均可以用系统对单位脉冲的响应来表示,即线性时不变系统的单位脉冲响应完全刻画了系统的特征 [16]。其原理见图1:
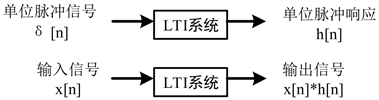
Figure 1. Impulse response theory of LTI system
图1. LTI系统冲激响应原理图
根据图1,LTI系统对任意输入信号x[n]的输出y[n]可以用输入信号与单位脉冲响应h[n]的卷积来表示:
[16] (8)
基于以上原理,可以创建单位脉冲信号进行一次正演计算获得模型的单位脉冲响应,然后用各个频率的发射信号和单位脉冲响应做卷积,便可得到各个频率信号对应的输出信号。由此相当于只进行了一次正演计算,正演效率得到成倍提升。
3. 模型正演算例
3.1. 二维地质模型构建
设置的模型为二维层状模型见图2,模型大小为10 m × 4.2 m,网格步长为0.005 m。上面一层为介质1,层厚2 m,下面一层为介质2,层厚2 m,在模型中间位置有一半径为0.3 m的圆形空洞,各介质的物性参数见表1。发射点位置在x = 0.1 m,y = 4 m处,接收点位置在x = 0.2 m,y = 4 m处,发射点和接收点移动步长为0.05 m。共采集194道数据,每道数据采样点数为8192个(时窗96 ns)。

Table 1. Electrical parameters of media in model
表1. 模型介质电性参数表
3.2. 发射信号生成及反射信号获取
选取的步进频率范围为100 MHz~300 MHz,步长1 MHz,一共有201个频率。
发射信号在Matlab中生成,每个频点上发射的信号形式见图3 (以100 MHz频率为例):
如图3所示,为了避免在正演结果中引入高频噪声,需要控制信号幅度从零缓慢增大,即发射信号形式表示为:
(9)
其中k取小于1的常数,k越小,信号幅度增大得越慢。
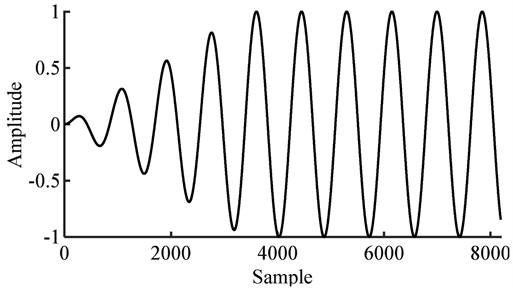
Figure 3. Transmit signal of 100 MHz
图3. 频率为100 MHz的发射信号
为了获得模型的单位脉冲响应,创建以下单位脉冲信号:
(10)
其中,dt为公式(7)控制的时间步长。
将以上单位脉冲信号作为发射信号进行正演,得到194个位置的单位脉冲响应,然后用生成的每个频率的发射信号与单位脉冲响应做卷积,即得到每个频率对应的反射信号。
为了验证该方法的准确性,用图3的连续波信号作为发射信号在第一道的位置进行正演,得到一道反射信号(见图4),将该反射信号和由图3的信号与单位脉冲响应做卷积得到的信号(见图5)做对比,分贝误差见图6。由误差对比可以看出,由冲激响应得到的反射信号和正演得到的反射信号的误差在−200 dB以下,这个误差范围是可以接受的。因此可以用这种方法得到每个频率的反射信号,正演效率得到提升,尤其是模型设置越大,频点数越多,效率提升越明显。
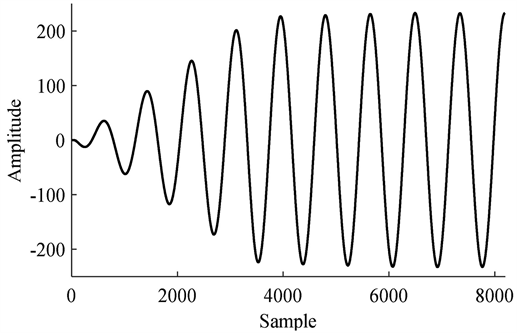
Figure 4. Reflected signal from simulation of Figure 3
图4. 由图3信号正演得到的第1道反射信号
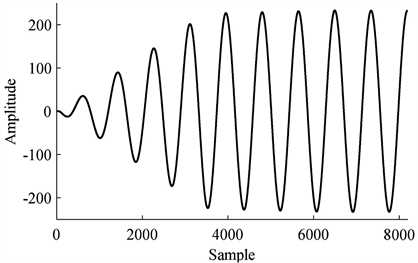
Figure 5. Signal from convolution of Figure 3 and impulse response
图5. 由图3信号和第1道冲激响应卷积得到的信号
3.3. 信号处理与融合
SFCW探地雷达正演的流程见图7,通过正演得到反射信号后,需要将得到的反射信号进行正交分解。其中同相分量I和正交分量Q分别由以下公式得到:
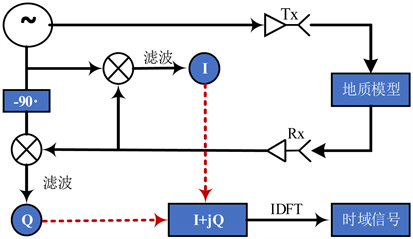
Figure 7. Flow of SFCW GPR modeling
图7. SFCW探地雷达正演流程
(11)
(12)
对I路信号和Q路信号分别用截至频率为f的低通滤波器进行处理,得到两路有用的基带信号:
(13)
(14)
则接收信号在频域内可表示为:
(15)
对于n个频点产生的频域序列Rx(n),通过逆傅里叶变换转到时域内合成单道时域信号。
第1道位置合成的数据见图8,转换到时域内后,层位界面反射信号出现在约36 ns的位置,对应的深度为2.0394 m,这与模型设置的界面在2 m深度处是符合的。
4. SFCW和脉冲体制雷达抗噪性能对比
将SFCW和脉冲信号分别用于正演,通过加入噪声对比其抗噪性能。选用的脉冲信号为中心频率为200 MHz的Ricker子波。
噪声按以下方法进行添加:对于Ricker子波信号,在其每道反射信号中添加噪声,然后合成Bscan图像;对于SFCW信号,在其每个频点的连续波反射信号中加入同等程度噪声,然后根据图7进行处理转换到时域内合成单道数据,再合成Bscan图像。正演结果需要进行增益处理以凸显深部弱反射信号,所以还需要控制相同的增益处理,以保证结果具有对比性。得到的结果分别见图9和图10。
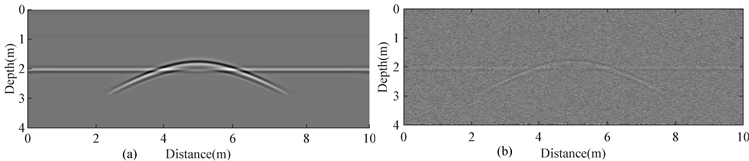
Figure 9. The simulation result of Ricker wave signal (a) Result without noise; (b) Result with noise
图9. Ricker子波信号正演结果。(a) 无噪声结果;(b) 有噪声结果
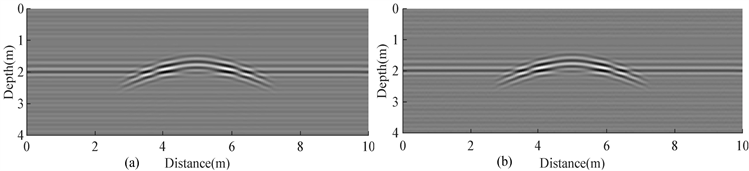
Figure 10. The simulation result of SFCW signal (a) Result without noise; (b) Result with noise
图10. SFCW信号正演结果。(a) 无噪声结果;(b) 有噪声结果
从Bscan结果(见图9(a)及图10(a))可以看出,在无噪声干扰时,两种信号正演结果都较好地反映了模型中的分层信息和异常体位置,空洞异常在两个Bscan图像上都表现为双曲线形状。成较大影响,由此说明SFCW信号用于探地雷达相比于脉冲信号具有更强的抗噪性能。在加入噪声条件下,Ricker子波信号正演结果信噪比明显下降(见图9(b)),层位界面和空洞的反射信号几乎被噪声掩盖,异常信息难以辨认;而对于SFCW信号正演结果来说,加入噪声后层位界面和空洞的反射信号仍保持高信噪比,异常特征清晰(见图10(b))。即加在每个频点连续波上的噪声对合成的时域信号并无造成较大影响,由此说明SFCW信号用于探地雷达相比于脉冲信号具有更强的抗噪性能。
5. 结论
本文通过对SFCW探地雷达进行数值模拟研究,得到结论如下:
1) SFCW信号用于探地雷达探测时,主要是将目标距离信息转化为不同频点连续波的相移,再通过逆傅里叶变换转换到时域内进行信号融合,以实现对目标体的检测;
2) 将SFCW信号进行正演计算时,结合LTI系统的冲激响应,在保证精度的条件下,可以避免重复进行正演计算,提高正演效率;
3) 根据对SFCW信号和Ricker子波脉冲信号的抗噪性能对比研究表明,在同样的噪声条件下,SFCW探地雷达结果具有更高的信噪比,抗噪性能更好。
基金项目
国家自然科学基金项目(42074171)、湖南省自然科学基金项目(2019JJ40371)联合资助。
NOTES
*第一作者。
#通讯作者。