1. 引言
脑梗死是生活中最常见的缺血性脑血管疾病,是由于各种原因造成脑动脉闭塞,引起相应供血区域脑细胞缺血、缺氧、坏死,从而出现相应功能的障碍。其中脑血栓是脑梗死最常见的一种类型,也是对脑部致命的损害,即使患者被救治回来,也多有失语、偏瘫、视物不清等后遗症状。脑血栓是由于身体其他部位血管内形成栓子后,随血液流动进入脑部血管造成堵塞,其中最常见的原因是颈部大血管动脉粥样硬化 [1]。动脉粥样硬化使得血管越来越窄,血脂过高,血栓不断形成。当脑血管和凝结的血栓聚在一起,就形成了脑血栓。
由于脑血栓等众多血管疾病的形成与动脉中的血液流动特性有着很大的关系,因此在过去的几十年来,人们对动脉中的血液流动从理论上、实验上、数值上进行了大量的研究。动脉的几何形状如狭窄、分叉等都是影响血液流动的重要因素,它很明显地影响了动脉中的局部血液动力学特性。狭窄会改变局部血液动力学特性,同时改变了的局部血液动力学又会引起血管的再狭窄发生 [2]。并且大量的临床实例表明,动脉血管的分叉处是病变的高发区域,最重要的原因之一是分叉处血流状态的改变。因为一旦发生病变,该区域的血液流动规律也将相应地发生改变,这将使得该病变进一步发展 [3]。在近年来的研究中,N. Beratlis等 [4] 对典型狭窄脉动中的血液流动进行了数值和实验研究。Farzan Ghalichi等 [5] 采用低雷诺湍流模型对健康狭窄颈动脉分叉中的生理脉动流进行数值模拟。Sonu S. Varghese等 [6] 强调了狭窄表面形态对血液流动的影响,用两种不同的实验模拟了脉动流过轴对称狭窄的过程。阚静等 [7] 通过对狭窄血管分叉局部的速度、动脉壁面剪切应力进行研究,分析冠状动脉分叉病变模型的血液动力学特性。刘赵淼等 [8] 以不同的Y型分叉冠状动脉血管为基础,研究了分叉角度及血液黏度对血流速度场、壁面剪应力、壁面压强的影响。
血流动力学数值模拟主要目的是揭示动脉血流动力学因素与动脉粥样硬化、血栓等动脉疾病之间的关系。特别是当在体或离体实验研究不可行时,数值模拟就成为惟一的可行手段。虽然仅仅依靠血流动力学的数值模拟结果,还不能完全解释有关动脉疾病,但这些数值模拟结果的确有助于人们更好地理解动脉疾病发生和发展的生理和病理基础 [9]。因此,深入分析狭窄分叉血管中的血流特性对医学会诊和临床治疗都具有重要的意义。故本文采用计算流体力学(CFD)方法,从血液流动动力学角度,通过研究不同狭窄程度对血液流动特性的影响来分析Y型分叉血管中血液流动改变对动脉血栓形成的影响。
2. 模型建立
2.1. 几何模型
本文以颈动脉血管为研究对象,颈部动脉直径一般为5.5~7.5 mm,故本文选取血管母管直径为6 mm,两条支管的血液流量比为1:1。根据能量消耗最小原则下的血管分支几何形状的结果 [10] 确定支管的直径为4.8 mm,分支角度
,以此建立血管Y型对称分支的几何模型,如图1所示。

Figure 1. Schematic diagram of the vascular branch geometry model
图1. 血管分支几何模型示意
2.2. 数学模型
2.2.1. 粘性不可压缩Navier-Stokes方程
本文假定血管壁是刚性的,这是因为如果动脉发生狭窄,动脉壁就会发生复杂的生理病变,一般来说,管壁弹性将大大减小,此时血管壁可作为刚性管壁处理 [11]。
对刚性动脉血管中的血液流动作如下假设:
(1) 血液是不可压缩的流体;
(2) 血液是均质的牛顿流体;
(3) 流动是充分发展的轴对称层流。
故血液流动的控制方程可取为粘性不可压缩的Navier-Stokes方程,即
(1)
其中:速度
;
分别为血液流动的水平、竖直方向速度;
分别为血液的密度、流场压力和黏性系数。
由于本文分析某一时刻血管中血液的流动情况,所以不考虑时间t的影响。故考虑二维区域内的Navier-Stokes方程组:
(2)
并且基于上述假设的二维血液质量守恒方程可表示为
(3)
2.2.2. 边界条件
在血管内表面上,运动方程满足无滑移条件:
,出口静压设为0。
2.2.3. 参数选取
根据表1,取血液密度为1055 kg∙m−3,血液粘度为4.012 mPa∙s。

Table 1. Related parameters of blood [12]
表1. 血液的相关参数 [12]
3. 数值模拟
3.1. 恒定初始速度对无病变血管壁压力的影响
现假设血管壁内表面无病变发生,入口初始速度为恒定速度0.5 m/s,模拟得到对应的血液流动的速度流线图和压力分布图,如图2所示。
 (a)
(a)  (b)
(b)
Figure 2. Flow line diagram and pressure diagram of blood flow when v = 0.5 m/s. (a) Velocity streamline diagram; (b) Pressure distribution diagram
图2. v = 0.5 m/s时血液流动流线图和压力图。(a) 速度流线图;(b) 压力分布图
分析图2可知,血液在血管中流动,在血管分叉交接位置处速度会发生突变,形成一个低速度区域,并且还伴随着局部涡流的产生,同时该位置附近的壁面压力会突然增大。从流体力学角度分析,这是由于血流速度在该处突然改变方向,因此血液必然会受到一个改变速度的力,该力的反作用力即为壁面压力 [3]。高壁面压力对血管壁内膜损伤较严重,使得在这一区域内聚集的血小板和血细胞粒子由于凝聚酶的作用附着在损伤的壁面上,促进炎症发生,从而形成血栓。并且随着时间的推移,血栓牢固结合在血管壁上,使血管狭窄,造成血管堵塞。
3.2. 不同程度动脉狭窄对血管内血液流动的影响
由3.1的分析知,血液的流速在血管分叉交接处会发生改变,所以当血管发生狭窄病变时,血液流经狭窄位置,速度也会发生变化。由文献 [13] 可知,当血流速度的分布呈抛物线型时,其速度达到稳定,不再改变。因此,为了更加单纯地研究动脉狭窄程度对血流的影响,本文直接假设血管入口边界上每个点的初始速度分布是抛物线型的,入口流速取为:
。
假设在Y型血管母管内壁中心对称位置附着一个近似半圆的突起,记其半径为R,则动脉狭窄的程度可用突起半圆的半径与血管半径的比值来描述,记为K。取R = 0.3 mm、0.4 mm、0.5 mm和1.5 mm,则K = 10.0%、13.3%、16.7%和50%。模拟得到对应血液流动的速度流线图和压力分布图,如图3~6所示。
 (a)
(a) 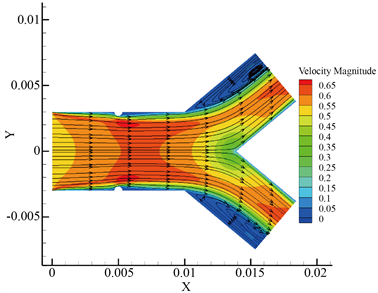 (b)
(b)
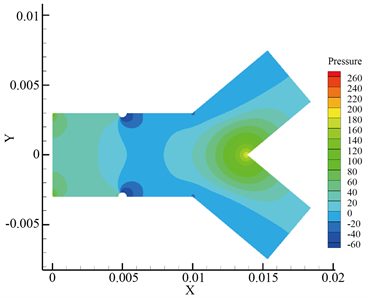
Figure 3. Pressure graph and streamline graph of blood flow at K = 10.0%. (a) Velocity streamline diagram; (b) Pressure distribution diagram
图3. K = 10.0%时血液流动流线图和压力图。(a) 速度流线图;(b) 压力分布图
 (a)
(a)  (b)
(b)
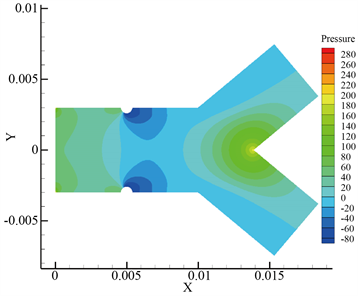
Figure 4. Pressure graph and streamline graph of blood flow at K = 13.3%. (a) Velocity streamline diagram; (b) Pressure distribution diagram
图4. K = 13.3%时血液流动流线图和压力图。(a) 速度流线图;(b) 压力分布图
分析同一狭窄程度下的速度流线图和压力分布图可知,血液在流经狭窄区域时,会产生分流现象,形成低速区域,甚至在狭窄区域附近形成局部涡流。并且壁面压力在母管狭窄周围区域、分叉交接处迅速变化,这就增加了血液在该区域的停留时间,导致血液中血小板和血细胞粒子在这一区域发生堆积,进而形成更严重的动脉狭窄 [14]。
 (a)
(a) 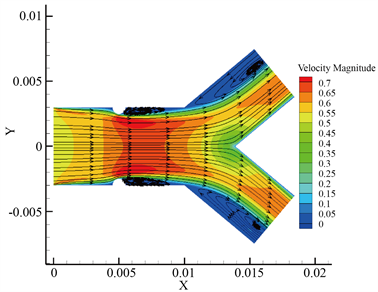 (b)
(b)
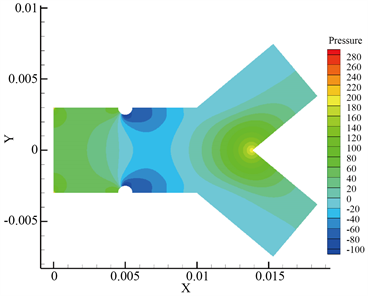
Figure 5. Pressure graph and streamline graph of blood flow at K = 16.7%. (a) Velocity streamline diagram; (b) Pressure distribution diagram
图5. K = 16.7%时血液流动流线图和压力图。(a) 速度流线图;(b) 压力分布图
 (a)
(a) 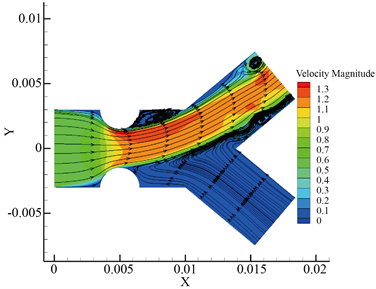 (b)
(b)
Figure 6. Pressure graph and streamline graph of blood flow at K = 50%. (a) Velocity streamline diagram; (b) Pressure distribution diagram
图6. K = 50%时血液流动流线图和压力图。(a) 速度流线图;(b) 压力分布图
分析不同狭窄程度下的速度流线图和压力分布图可知,随着狭窄区域的不断增大,低速区不断增大,涡流的面积不断增大,所以涡流的面积大小和狭窄病变的程度有着密切联系。当K = 10%时,也就是动脉局部狭窄的初期阶段,低速区非常小,几乎不产生涡流,因此动脉狭窄的存在对血液流动特性的影响是比较小的。当K = 13.3%时,低速区域增大,开始产生涡流,并且涡流是在低速区的右侧产生的,这是因为在低速区右侧压力发生突变。当K = 16.7%时,涡流面积增大,使得血液中血小板和血细胞粒子堆积的区域增大,进而扩大血栓形成的区域。而当K = 50%,即狭窄达到一定程度时,速度几乎不呈抛物线分布,此时速度流线紊乱,分布已不满足轴对称层流规律。
4. 结论
本文利用血液流动的粘性不可压缩N-S方程模型,采用计算流体方法分别对无病变血管及血管狭窄程度为K = 10%、13.3%、16.7%和50%的Y型分叉动脉模型的血液流动进行了数值模拟,分别计算出了相应血液流动的流线图及压力图,并对数值结果做了具体的分析。
(1) 当血液流过分叉交接位置时,速度会发生突变,形成低速度区域,并伴随着局部涡流的产生。同时该位置附近的壁面压力突然增大,对血管壁内膜造成损伤,使得在这一区域内聚集的血小板和血细胞粒子由于凝聚酶的作用附着在损伤的壁面上,该位置处即是研究的“最适成栓位置” [15]。
(2) 当血液流经狭窄区域时,会产生分流现象,形成低速区域,甚至在狭窄区域附近形成局部涡流。并且壁面压力的峰值出现在狭窄所在坐标附近,这是由于狭窄位置附近,血液流速明显变大,从而对壁面的压力显著增加,这与梅立泉和赵柯 [16] 对狭窄血管内血液流动所做过的理论分析基本一致。
(3) 分析不同狭窄程度对血流的影响可知,狭窄程度越大,涡流面积越大,并且当狭窄达到一定程度时,血液流动速度发生紊乱,不满足轴对称层流规律,从而形成血栓的可能性更大。
从上述分析可以看出,血栓的发病机制和病变的发展与血流动力学特征密切相关。本文为研究血栓的形成和发展提供了科学的方法,有利于为制定临床治疗方案提供客观依据。由于目前尚没有成熟的技术可以直接观察和测量人体动脉血管中的血流细节,因此在研究时,本文假定血液为不可压缩的牛顿流体,血管壁为不可渗透的刚性管壁。与真实血管中的血流相比,研究结果仅是血流过程的近似理论结果。在未来的研究中,将建立更加符合临床实际情况的三维动脉分叉血管模型。
基金项目
内蒙古大学校级大学生创新创业训练计划资助项目(202011216)。
NOTES
*通讯作者。