鲁洛克斯三角形上的Schwarz边值问题

Schwarz Boundary Value Problem on Reuleaux Triangle

摘要: 本文给出了鲁洛克斯三角形上一类特殊函数——其实部在边界上是循环对称函数——的Schwarz边值问题的解法，首先根据这类函数的特殊性将原问题进行改造，使其分别转化为实部在边界上关于实轴对称的Schwarz边值问题和实部在边界上关于实轴反对称的Schwarz边值问题，我们发现改造后的两个问题解之和就是原问题的解，然后通过对称扩张将改造后的两个问题转换为两组Riemann边值问题，最后通过求解这两组Riemann边值问题得到原问题的解。

Abstract: This paper presents the approach to the Schwarz boundary value problem of a special function on the Reuleaux triangle, the real part of this function is a cyclosymmetric function on the boundary. According to the particularity of this type of function, the original problem is first transformed into a Schwarz boundary value problem with the real part symmetric about the real axis on the boundary and the real part antisymmetric Schwarz boundary value problem with the real axis on the boundary. The sum of the solutions of these two problems is equal to the solution of the original problem. After that, the two problems after the conversion are further converted into two sets of Riemann boundary value problems through the symmetric expansion, finally, the solution of the original problem is obtained by solving the solutions of the two sets of Riemann boundary value problems.

1. 引言

记 $D_0=\left\{z\in ℂ|\left|z+1\right|<\sqrt{3},\left|z-\frac{1+i\sqrt{3}}{2}\right|<\sqrt{3},\left|z-\frac{1-i\sqrt{3}}{2}\right|<\sqrt{3}\right\}$，其边界 $L=L_1+L_2+L_3$，如图1所示。其中 $a=\frac{1+i\sqrt{3}}{2},b=-1,c=\frac{1-i\sqrt{3}}{2}$，

Figure 1. Reuleaux triangle

图1. 鲁洛克斯三角形

$D_1=\left\{z\in ℂ|\left|z-\frac{1+i\sqrt{3}}{2}\right|>\sqrt{3},Im\left(z\right)<0,\mathrm{Re}\left[\left(\sqrt{3}-i\right)z\right]<0\right\}$

$D_2=\left\{z\in ℂ|\left|z+1\right|>\sqrt{3},\mathrm{Re}\left[\left(\sqrt{3}+i\right)z\right]<0<\mathrm{Re}\left[\left(\sqrt{3}-i\right)z\right]\right\}$

$D_3=\left\{z\in ℂ|\left|z-\frac{1-i\sqrt{3}}{2}\right|>\sqrt{3},Im\left(z\right)>0,\mathrm{Re}\left[\left(\sqrt{3}+i\right)z\right]>0\right\}$

定义1 [1]：设 $f\left(t\right)$ 定义于(开口或封闭的)光滑曲线 $L$ 上，若对 $L$ 上任意两点 $t^{\prime },t^{″}$，恒有

其中 $A,\alpha$ 都是确定的常数，则称 $f\left(t\right)$ 在 $L$ 上满足 $\alpha$ 阶的Hölder条件或 $H^{\alpha }$ 条件，记为 $f\in H^{\alpha }\left(L\right)$ 或简记为 $\in H^{\alpha }$，而 $\alpha$ 称为Hölder指数，若不强调指出指数 $\alpha$，也可简记为 $f\left(t\right)\in H\left(L\right)$。

定义2 [1] [2]：设 $f\left(t\right)$ 是在射线 $L^{*}$ 上的连续复函数。如果：

1) 在任意有限闭区间 $I\subset L^{*}$ 上 $f\left(t\right)\in H^{\mu }$

2) 在 $\infty$ 的邻域 $U\left(\infty \right)$ 内满足条件

$\left|f\left(t\right)-f\left(t^{\prime }\right)\right|\le A{\left|\frac{1}{t}-\frac{1}{t^{\prime }}\right|}^{\mu }\left(0<\mu \le 1\right),t,t^{\prime }\in L^{*}\cap U(\; \infty \; )$

则称 $f\left(t\right)\in {\hat{H}}^{\mu }\left(L^{*}\right)$，或简记为 ${\hat{H}}^{\mu }$。若不强调 $\mu$，可记为 $\hat{H}$。

注 [2]：若 $f\in {\hat{H}}^{\mu }\left(L^{*}\right)$ 且 $f\left(\infty \right)=0$，我们记为 $f\in {\hat{H}}_0^{\mu }\left(L^{*}\right)$ 或简记为 $f\in {\hat{H}}_0\left(L^{*}\right)$。

2. 提出问题

求在 $D_0$ 内的全纯函数 ${\text{Φ}}_0^{+}\left(z\right)=u\left(z\right)+iv\left(z\right)$，连续到 $D_0+L$ 上，满足边值条件

$\mathrm{Re}\left[{\text{Φ}}_0^{+}\left(t\right)\right]=f\left(t\right),t\in L$ (1)

其中 $f\left(t\right)$ 是已给在L上 $\in H$ 的实函数。为简单起见，我们假设

$f\left(t\right)=f\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)$

3. 问题转化

令

${\text{Ψ}}_0\left(z\right)=\frac{1}{2}\left[{\text{Φ}}_0\left(z\right)+\overline{{\text{Φ}}_0\left(\stackrel{¯}{z}\right)}\right]$

${\text{Ω}}_0\left(z\right)=\frac{1}{2}\left[{\text{Φ}}_0\left(z\right)-\overline{{\text{Φ}}_0\left(\stackrel{¯}{z}\right)}\right]$

代入(1)式，得到

$\mathrm{Re}\left[{\text{Ψ}}_0\left(t\right)\right]=\frac{1}{2}\left[f\left(t\right)+f\left(\bar{t}\right)\right]:=\tilde{f}\left(t\right)$ (2)

$\mathrm{Re}\left[{\text{Ω}}_0\left(t\right)\right]=\frac{1}{2}\left[f\left(t\right)-f\left(\bar{t}\right)\right]:=\widetilde{\stackrel{˜}{f}}\left(t\right)$ (3)

由上述定义可知， $\tilde{f}$ 关于实轴对称， $\widetilde{\stackrel{˜}{f}}$ 关于实轴反对称，即

$\tilde{f}\left(\bar{t}\right)=\tilde{f}(\; t\; )$

$\widetilde{\stackrel{˜}{f}}\left(\bar{t}\right)=-\widetilde{\stackrel{˜}{f}}(\; t\; )$

再由 $f\left(t\right)=f\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)$ 可知

$\tilde{f}\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\frac{1}{2}\left[f\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)+f\left(\overline{t\cdot {\text{e}}^{i\frac{2\pi }{3}}}\right)\right]=\frac{1}{2}\left[f\left(t\right)+f\left(\overline{t\cdot {\text{e}}^{i\frac{2\pi }{3}}}\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)\right]=\tilde{f}(\; t\; )$

同理可知，

$\widetilde{\stackrel{˜}{f}}\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\widetilde{\stackrel{˜}{f}}(\; t\; )$

定义3：若 $z$ 与 $z^{\star }$ 满足

$z^{\star }-z_0=\frac{R^2}{\bar{z}-\overline{z_0}}$

则称 $z$ 与 $z^{\star }$ 关于 $L:\left|z-z_0\right|=R$ 互为对称点。

我们令 [3] [4] [5]

${\tau }_1\left(z\right)=\frac{\left(1+i\sqrt{3}\right)\bar{z}+4}{2\bar{z}-\left(1-i\sqrt{3}\right)}$

${\tau }_2\left(z\right)=\frac{2-\bar{z}}{\bar{z}+1}$

${\tau }_3\left(z\right)=\frac{\left(1-i\sqrt{3}\right)\bar{z}+4}{2\bar{z}-\left(1+i\sqrt{3}\right)}$

则， ${\tau }_1\left(z\right)$ 与 $z$ 关于 $C_a:\left|z-a\right|=\sqrt{3}$ 互为对称点， ${\tau }_2\left(z\right)$ 与 $z$ 关于 $C_b:\left|z-b\right|=\sqrt{3}$ 互为对称点， ${\tau }_3\left(z\right)$ 与 $z$ 关于 $C_c:\left|z-c\right|=\sqrt{3}$ 互为对称点。

由 [1] 可知，通过构造对称扩张可以将Schwarz边值问题等价转化为Riemann边值问题。下面我们给出 ${\text{Ψ}}_0\left(z\right)$ 在外域 $D_1,D_2,D_3$ 中的对称扩张，如下

${\text{Ψ}}_1\left(z\right)=\overline{{\text{Ψ}}_0\left({\tau }_1\left(z\right)\right)},z\in D_1$

${\text{Ψ}}_2\left(z\right)=\overline{{\text{Ψ}}_0\left({\tau }_2\left(z\right)\right)},z\in D_2$

${\text{Ψ}}_3\left(z\right)=\overline{{\text{Ψ}}_0\left({\tau }_3\left(z\right)\right)},z\in D_3$

记

$\text{Ψ}\left(z\right)=\{\begin{array}{c}{\text{Ψ}}_0\left(z\right),z\in D_0\\ {\text{Ψ}}_1\left(z\right),z\in D_1\\ {\text{Ψ}}_2\left(z\right),z\in D_2\\ {\text{Ψ}}_3\left(z\right),z\in D_3\end{array}$

易证， $\text{Ψ}\left(z\right)$ 是一分区全纯函数。

类似的，我们给出 ${\text{Ω}}_0\left(z\right)$ 在外域 $D_1,D_2,D_3$ 中的对称扩张，如下

${\text{Ω}}_1\left(z\right)=\overline{{\text{Ω}}_0\left({\tau }_1\left(z\right)\right)}$

${\text{Ω}}_2\left(z\right)=\overline{{\text{Ω}}_0\left({\tau }_2\left(z\right)\right)}$

${\text{Ω}}_3\left(z\right)=\overline{{\text{Ω}}_0\left({\tau }_3\left(z\right)\right)}$

记

$\text{Ω}\left(z\right)=\{\begin{array}{c}{\text{Ω}}_0\left(z\right),z\in D_0\\ {\text{Ω}}_1\left(z\right),z\in D_1\\ {\text{Ω}}_2\left(z\right),z\in D_2\\ {\text{Ω}}_3\left(z\right),z\in D_3\end{array}$

易证， $\text{Ω}\left(z\right)$ 是一分区全纯函数。

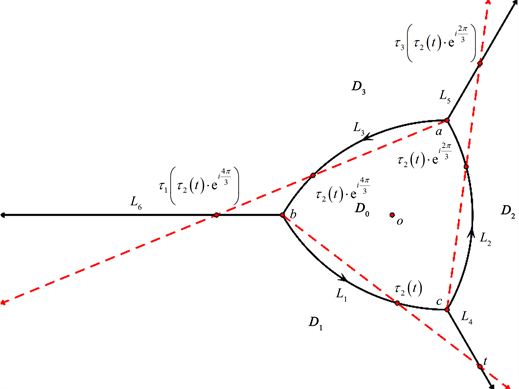
Figure 2. Positive boundary value and its equivalent relation

图2. 正边值及其等价关系

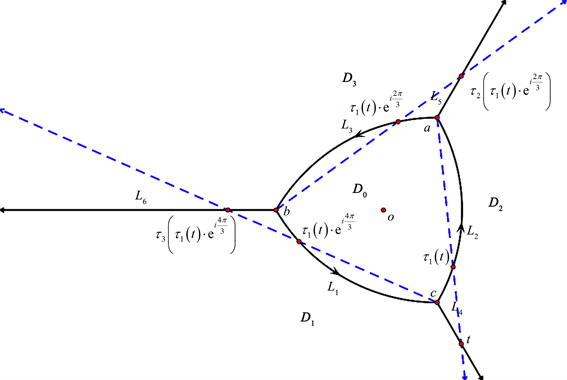
Figure 3. Negative boundary value and its equivalent relation

图3. 负边值及其等价关系

如图2和图3所示，通过计算可以得到如下性质：

${\tau }_1\left(\bar{z}\right)=\overline{{\tau }_3\left(z\right)}$

${\tau }_2\left(\bar{z}\right)=\overline{{\tau }_2\left(z\right)}$

${\tau }_2\left(z\right)\cdot {\text{e}}^{i\frac{2\pi }{3}}={\tau }_3\left(z\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)$

${\tau }_2\left(z\right)\cdot {\text{e}}^{i\frac{4\pi }{3}}={\tau }_1\left(z\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)$

${\tau }_1\left(z\right)\cdot {\text{e}}^{i\frac{4\pi }{3}}={\tau }_3\left(z\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)$

其中 $z\in D_0+L$。如图4所示，有

$\tilde{f}\left({\tau }_2\left(t\right)\right)=\tilde{f}\left({\tau }_2\left(t\right)\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)=\tilde{f}\left({\tau }_1\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)\right),t\in L_4$

$\tilde{f}\left({\tau }_1\left(t\right)\right)=\tilde{f}\left({\tau }_1\left(t\right)\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)=\tilde{f}\left({\tau }_3\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)\right),t\in L_4$

${\tau }_1\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)=\overline{{\tau }_3\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)}$

可得

$\tilde{f}\left({\tau }_2\left(t\right)\right)=\tilde{f}\left({\tau }_3\left(t\right)\right),t\in L_4$

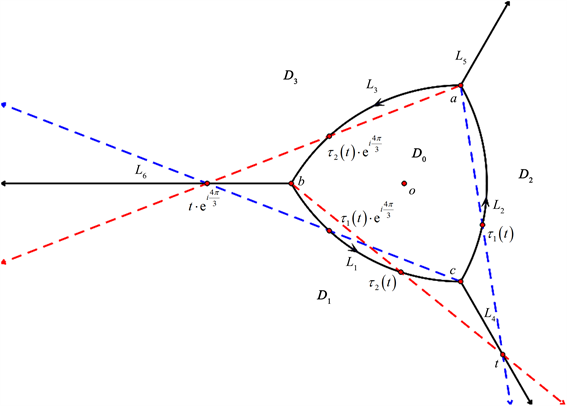
Figure 4. The boundary value problem on L₄

图4. L₄上的边值问题

同理，如图5所示，有

$\tilde{f}\left({\tau }_3\left(t\right)\right)=\tilde{f}\left({\tau }_3\left(t\right)\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\tilde{f}\left({\tau }_1\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)\right),t\in L_5$

$\tilde{f}\left({\tau }_2\left(t\right)\right)=\tilde{f}\left({\tau }_2\left(t\right)\cdot {\mathrm{e}}^{i\frac{2\pi }{3}}\right)=\tilde{f}\left({\tau }_3\left(t\cdot {\mathrm{e}}^{i\frac{2\pi }{3}}\right)\right),t\in L_5$

${\tau }_1\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\overline{{\tau }_3\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)}$

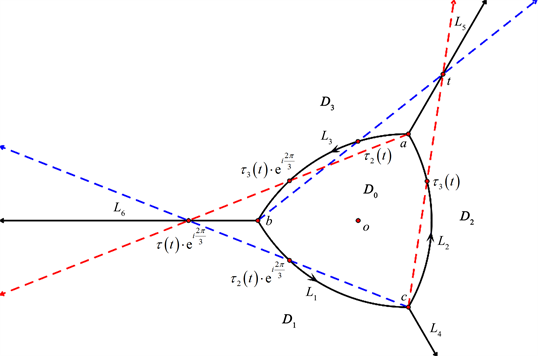
Figure 5. The boundary value problem on L₅

图5. L₅上的边值问题

可得

$\tilde{f}\left({\tau }_3\left(t\right)\right)=\tilde{f}\left({\tau }_2\left(t\right)\right),t\in L_5$

这就意味着，所求函数 $\text{Ψ}$ 在 $L_4,L_5,L_6$ 上正负边值的实部相等，接下来我们将讨论其虚部之间的关系。

设

${\text{Ψ}}_0\left(z\right)=u\left(z\right)+iv(\; z\; )$

我们有

$v\left(x_0,y_0\right)={\displaystyle {\int }_{\left(0,0\right)}^{\left(x_0,y_0\right)}{v}_x\text{d}x}+v_y\text{d}y+v\left(0,0\right)$

由C-R方程可得

$\begin{array}{c}v\left(x_0,y_0\right)={\displaystyle {\int }_{\left(0,0\right)}^{\left(x_0,y_0\right)}-u_y\text{d}x+u_x\text{d}y+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\nabla u\cdot \left(\text{d}y,-\text{d}x\right)}+v\left(0,0\right)\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\nabla u\cdot n\text{d}S}+v\left(0,0\right)\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\frac{\partial u}{\partial n}\text{d}S}+v\left(0,0\right)\end{array}$

记 $\left({x^{\prime }}_0,{y^{\prime }}_0\right)$ 是 $\left(x_0,y_0\right)$ 关于 $L_4$ 的对称点，有

$\begin{array}{c}v\left({x^{\prime }}_0,{y^{\prime }}_0\right)={\displaystyle {\int }_{\left(0,0\right)}^{\left({x^{\prime }}_0,{y^{\prime }}_0\right)}{v}_x\text{d}x+v_y\text{d}y+v\left(0,0\right)}\\ ={\displaystyle {\int }_{\left(0,0\right)}^{\left({x^{\prime }}_0,{y^{\prime }}_0\right)}-u_y\text{d}x+u_x\text{d}y+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_2}\nabla u\cdot \left(\text{d}y,-\text{d}x\right)+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_2}\nabla u\cdot n\text{d}S+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_2}\frac{\partial u}{\partial n}\text{d}S+v\left(0,0\right)}\\ =-{\displaystyle {\int }_{{\text{Γ}}_1}\frac{\partial u}{\partial n}\text{d}S+v\left(0,0\right)}\end{array}$

其中 ${\text{Γ}}_1$ 是 $\left(0,0\right)$ 到 $\left(x_0,y_0\right)$ 的直线段， ${\text{Γ}}_2$ 是 $\left(0,0\right)$ 到 $\left({x^{\prime }}_0,{y^{\prime }}_0\right)$ 的直线段。从而，有

${\text{Ψ}}_2^{+}\left(t\right)-\tilde{f}\left({\tau }_2\left(t\right)\right)=-\left[{\text{Ψ}}_1^{-}\left(t\right)-\tilde{f}\left({\tau }_1\left(t\right)\right)\right]+C,t\in L_4$

同理，我们有

${\text{Ψ}}_3^{+}\left(t\right)-\tilde{f}\left({\tau }_3\left(t\right)\right)=-\left[{\text{Ψ}}_2^{-}\left(t\right)-\tilde{f}\left({\tau }_2\left(t\right)\right)\right]+C,t\in L_5$

${\text{Ψ}}_1^{+}\left(t\right)-\tilde{f}\left({\tau }_1\left(t\right)\right)=-\left[{\text{Ψ}}_3^{-}\left(t\right)-\tilde{f}\left({\tau }_3\left(t\right)\right)\right]+C,t\in L_6$

问题(2)在满足条件

$\begin{array}{c}{\text{Ψ}}_j^{-}\left(t\right)=\overline{{\text{Ψ}}_0^{+}\left(t\right)},t\in L_j,j=1,2,3\end{array}$ (4)

时，可等价转化为

$\{\begin{array}{l}{\text{Ψ}}_0^{+}\left(t\right)=-{\text{Ψ}}_1^{-}\left(t\right)+2\tilde{f}\left(t\right),t\in L_1\hfill \\ {\text{Ψ}}_0^{+}\left(t\right)=-{\text{Ψ}}_2^{-}\left(t\right)+2\tilde{f}\left(t\right),t\in L_2\hfill \\ {\text{Ψ}}_0^{+}\left(t\right)=-{\text{Ψ}}_3^{-}\left(t\right)+2\tilde{f}\left(t\right),t\in L_3\hfill \\ {\text{Ψ}}_2^{+}\left(t\right)=-{\text{Ψ}}_1^{-}\left(t\right)+2\tilde{f}\left({\tau }_2\left(t\right)\right)+C,t\in L_4\hfill \\ {\text{Ψ}}_3^{+}\left(t\right)=-{\text{Ψ}}_2^{-}\left(t\right)+2\tilde{f}\left({\tau }_3\left(t\right)\right)+C,t\in L_5\hfill \\ {\text{Ψ}}_1^{+}\left(t\right)=-{\text{Ψ}}_3^{-}\left(t\right)+2\tilde{f}\left({\tau }_1\left(t\right)\right)+C,t\in L_6\hfill \end{array}$ (5)

由

$\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)\right),t\in L_4$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)\right),t\in L_4$

${\tau }_1\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)=\overline{{\tau }_3\left(t\cdot {\text{e}}^{i\frac{4\pi }{3}}\right)}$

可得

$\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right)=-\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right),t\in L_4$

同理，由

$\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)\right),t\in L_5$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)\right),t\in L_5$

${\tau }_1\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)=\overline{{\tau }_3\left(t\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)}$

可得

$\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right)=-\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right),t\in L_5$

设

${\text{Ω}}_0\left(z\right)=u\left(z\right)+iv(\; z\; )$

我们有

$v\left(x_0,y_0\right)={\displaystyle {\int }_{\left(0,0\right)}^{\left(x_0,y_0\right)}{v}_x\text{d}x+v_y\text{d}y+v\left(0,0\right)}$

由C-R方程可得

$\begin{array}{c}v\left(x_0,y_0\right)={\displaystyle {\int }_{\left(0,0\right)}^{\left(x_0,y_0\right)}-u_y\text{d}x+u_x\text{d}y+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\nabla u\cdot \left(\text{d}y,-\text{d}x\right)+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\nabla u\cdot n\text{d}S+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\frac{\partial u}{\partial n}\text{d}S+v\left(0,0\right)}\end{array}$

记 $\left({x^{\prime }}_0,{y^{\prime }}_0\right)$ 是 $\left(x_0,y_0\right)$ 关于 $L_4$ 的对称点，有

$\begin{array}{c}v\left({x^{\prime }}_0,{y^{\prime }}_0\right)={\displaystyle {\int }_{\left(0,0\right)}^{\left({x^{\prime }}_0,{y^{\prime }}_0\right)}{v}_x\text{d}x+v_y\text{d}y+v\left(0,0\right)}\\ ={\displaystyle {\int }_{\left(0,0\right)}^{\left({x^{\prime }}_0,{y^{\prime }}_0\right)}-u_y\text{d}x+u_x\text{d}y+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_2}\nabla u\cdot \left(\text{d}y,-\text{d}x\right)+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_2}\nabla u\cdot n\text{d}S+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_2}\frac{\partial u}{\partial n}\text{d}S+v\left(0,0\right)}\\ ={\displaystyle {\int }_{{\text{Γ}}_1}\frac{\partial u}{\partial n}\text{d}S+v\left(0,0\right)}\end{array}$

其中 ${\text{Γ}}_1$ 是 $\left(0,0\right)$ 到 $\left(x_0,y_0\right)$ 的直线段， ${\text{Γ}}_2$ 是 $\left(0,0\right)$ 到 $\left({x^{\prime }}_0,{y^{\prime }}_0\right)$ 的直线段。我们假设 $v\left(0,0\right)=0$，从而有

${\text{Ω}}_2^{+}\left(t\right)-\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right)={\text{Ω}}_1^{-}\left(t\right)-\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\right),t\in L_4$

同理，我们有

${\text{Ω}}_3^{+}\left(t\right)-\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right)={\text{Ω}}_2^{-}\left(t\right)-\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right),t\in L_5$

${\text{Ω}}_1^{+}\left(t\right)-\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\right)={\text{Ω}}_3^{-}\left(t\right)-\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right),t\in L_6$

问题(3)在满足条件

$\begin{array}{c}{\text{Ω}}_j^{-}\left(t\right)=\overline{{\text{Ω}}_0^{+}\left(t\right)},t\in L_j,j=1,2,3\end{array}$ (6)

时，可等价转化为

$\{\begin{array}{l}{\text{Ω}}_0^{+}\left(t\right)=-{\text{Ω}}_1^{-}\left(t\right)+2\widetilde{\stackrel{˜}{f}}\left(t\right),t\in L_1\hfill \\ {\text{Ω}}_0^{+}\left(t\right)=-{\text{Ω}}_2^{-}\left(t\right)+2\widetilde{\stackrel{˜}{f}}\left(t\right),t\in L_2\hfill \\ {\text{Ω}}_0^{+}\left(t\right)=-{\text{Ω}}_3^{-}\left(t\right)+2\widetilde{\stackrel{˜}{f}}\left(t\right),t\in L_3\hfill \\ {\text{Ω}}_2^{+}\left(t\right)={\text{Ω}}_1^{-}\left(t\right)+2\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right),t\in L_4\hfill \\ {\text{Ω}}_3^{+}\left(t\right)={\text{Ω}}_2^{-}\left(t\right)+2\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right),t\in L_5\hfill \\ {\text{Ω}}_1^{+}\left(t\right)={\text{Ω}}_3^{-}\left(t\right)+2\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\right),t\in L_6\hfill \end{array}$ (7)

4. 求解问题

首先考虑开口弧段 $L_1$ 上的边值问题，由于 $G\left(t\right)\equiv -1$，我们取 $\log G\left(t\right)=i\pi$。引入函数

${\text{Γ}}_1\left(z\right)=\frac{1}{2}{\displaystyle {\int }_{{\text{Γ}}_1}\frac{\text{d}t}{t-z}},z\notin L_1$

由 [1] 可知，在端点附近有

${\text{Γ}}_1\left(z\right)=\{\begin{array}{l}-\frac{1}{2}\log \left(b-z\right)+{\text{Δ}}_b\left(z\right),z\in U\left(b,ϵ\right)\hfill \\ \frac{1}{2}\log \left(c-z\right)+{\text{Δ}}_c\left(z\right),z\in U\left(c,ϵ\right)\hfill \end{array}$

其中 ${\text{Δ}}_b\left(z\right),{\text{Δ}}_c\left(z\right)$ 分别在 $z=b,c$ 附近沿 $L_1$ 剖开的邻域 $N_b,N_c$ 中全纯。

令

${\chi }_1\left(z\right)={\text{e}}^{{\text{Γ}}_1(\; z\; )}$

有

${\chi }_1\left(z\right)=\{\begin{array}{c}{\left(b-z\right)}^{-\frac{1}{2}}+{\chi }_b\left(z\right),z\in U\left(b,ϵ\right)\\ {\left(c-z\right)}^{\frac{1}{2}}+{\chi }_c\left(z\right),z\in U\left(c,ϵ\right)\end{array}$

其中 ${\chi }_b,{\chi }_c$ 分别在 $N_b,N_c$ 中全纯。

我们假设在 $h_0$ 类中求解，可知 ${\lambda }_b=0,{\lambda }_c=-1$，典则函数为

$X_1\left(z\right)={\left(z-c\right)}^{-1}{\chi }_1(\; z\; )$

易得 ${\text{Ψ}}_0$ 在端点 $z=b,c$ 附近是 $-\frac{1}{2}$ 阶的极点。

同理可知， ${\text{Ψ}}_0$ 在 $L_2$ 的端点 $z=c,a$ 附近是 $-\frac{1}{2}$ 阶的极点， ${\text{Ψ}}_0$ 在 $L_3$ 的端点 $z=a,b$ 附近是 $-\frac{1}{2}$ 阶的极点。从而，由对称扩张的性质可以推出 $\text{Ψ}$ 在 $\infty$ 处是 $-\frac{1}{2}$ 阶的极点。

记 $\text{Σ}=L_4+L_5+L_6$，给出函数

$\text{Γ}\left(z\right)=\frac{1}{2}{\displaystyle {\int }_L\frac{\text{d}\tau }{\tau -z}}$

$W\left(z\right)={\left(z-a\right)}^{\frac{1}{2}}{\left(z-b\right)}^{\frac{1}{2}}{\left(z-c\right)}^{\frac{1}{2}}{\text{e}}^{\text{Γ}(\; z\; )}$

这里引用 [1] 中幂函数正负边值的定义

$W^{+}\left(t\right)=\{\begin{array}{c}{\left(t-a\right)}^{\frac{1}{2}}{\left(t-b\right)}^{\frac{1}{2}}{\left(t-c\right)}^{\frac{1}{2}}{\text{e}}^{{\text{Γ}}^{+}\left(t\right)},t\in L\\ {\left(t-a\right)}^{\frac{1}{2}}{\left(t-b\right)}^{\frac{1}{2}}{\left(t-c\right)}^{\frac{1}{2}}{\text{e}}^{\text{Γ}\left(t\right)},t\in \text{Σ}\end{array}$

$W^{-}\left(t\right)=\{\begin{array}{c}{\left(t-a\right)}^{\frac{1}{2}}{\left(t-b\right)}^{\frac{1}{2}}{\left(t-c\right)}^{\frac{1}{2}}{\text{e}}^{{\text{Γ}}^{-}\left(t\right)},t\in L\\ -{\left(t-a\right)}^{\frac{1}{2}}{\left(t-b\right)}^{\frac{1}{2}}{\left(t-c\right)}^{\frac{1}{2}}{\text{e}}^{\text{Γ}\left(t\right)},t\in \text{Σ}\end{array}$

方程组(5)两边同时除以 $W^{+}\left(t\right)$，得

$\{\begin{array}{l}\frac{{\text{Ψ}}_0^{+}\left(t\right)}{W^{+}\left(t\right)}=\frac{{\text{Ψ}}_1^{-}\left(t\right)}{W^{-}\left(t\right)}+\frac{2\tilde{f}\left(t\right)}{W^{+}\left(t\right)},t\in L_1\hfill \\ \frac{{\text{Ψ}}_0^{+}\left(t\right)}{W^{+}\left(t\right)}=\frac{{\text{Ψ}}_2^{-}\left(t\right)}{W^{-}\left(t\right)}+\frac{2\tilde{f}\left(t\right)}{W^{+}\left(t\right)},t\in L_2\hfill \\ \frac{{\text{Ψ}}_0^{+}\left(t\right)}{W^{+}\left(t\right)}=\frac{{\text{Ψ}}_3^{-}\left(t\right)}{W^{-}\left(t\right)}+\frac{2\tilde{f}\left(t\right)}{W^{+}\left(t\right)},t\in L_3\hfill \\ \frac{{\text{Ψ}}_2^{+}\left(t\right)}{W^{+}\left(t\right)}=\frac{{\text{Ψ}}_1^{-}\left(t\right)}{W^{-}\left(t\right)}+\frac{2\tilde{f}\left({\tau }_2\left(t\right)\right)}{W^{+}\left(t\right)},t\in L_4\hfill \\ \frac{{\text{Ψ}}_3^{+}\left(t\right)}{W^{+}\left(t\right)}=\frac{{\text{Ψ}}_2^{-}\left(t\right)}{W^{-}\left(t\right)}+\frac{2\tilde{f}\left({\tau }_3\left(t\right)\right)}{W^{+}\left(t\right)},t\in L_5\hfill \\ \frac{{\text{Ψ}}_1^{+}\left(t\right)}{W^{+}\left(t\right)}=\frac{{\text{Ψ}}_3^{-}\left(t\right)}{W^{-}\left(t\right)}+\frac{2\tilde{f}\left({\tau }_1\left(t\right)\right)}{W^{+}\left(t\right)},t\in L_6\hfill \end{array}$

其中

$\frac{2\tilde{f}\left({\tau }_2\left(t\right)\right)}{W^{+}\left(t\right)}\in H_{\rho }^{*}\left(c\right)\cap {\hat{H}}_0(\; L\; 4\; )$

$\frac{2\tilde{f}\left({\tau }_3\left(t\right)\right)}{W^{+}\left(t\right)}\in H_{\rho }^{*}\left(a\right)\cap {\hat{H}}_0(\; L\; 5\; )$

$\frac{2\tilde{f}\left({\tau }_1\left(t\right)\right)}{W^{+}\left(t\right)}\in H_{\rho }^{*}\left(b\right)\cap {\hat{H}}_0(\; L\; 6\; )$

由于

$Ord\left[\Psi ,\infty \right]=-\frac{1}{2}$

故

$Ord\left[\frac{\Psi }{W},\infty \right]=-1$

从而上述方程组的解为

$\frac{\text{Ψ}\left(z\right)}{W\left(z\right)}=\frac{1}{2\pi i}{\displaystyle {\int }_{L+\text{Σ}}\frac{2\tilde{f}\left(\tau \left(t^{+}\right)\right)}{W^{+}\left(t\right)\left(t-z\right)}\text{d}t}+\frac{{\lambda }_a}{z-a}+\frac{{\lambda }_b}{z-b}+\frac{{\lambda }_c}{z-c}$

$\text{Ψ}\left(z\right)=\frac{W\left(z\right)}{2\pi i}{\displaystyle {\int }_{L+\text{Σ}}\frac{2\tilde{f}\left(\tau \left(t^{+}\right)\right)}{W^{+}\left(t\right)\left(t-z\right)}\text{d}t}+W\left(z\right)\left(\frac{{\lambda }_a}{z-a}+\frac{{\lambda }_b}{z-b}+\frac{{\lambda }_c}{z-c}\right)$

为了满足条件(4)，需构造 ${\text{Ψ}}_{*}\left(z\right)$ [1]，我们令

${\text{Γ}}_{1*}\left(z\right)=\overline{{\text{Γ}}_1\left({\tau }_1\left(z\right)\right)}=\frac{1}{2}{\displaystyle {\int }_{L_1}\frac{\text{d}t}{t-z}}-{\displaystyle {\int }_{L_1}\frac{\text{d}t}{2t-\left(1+i\sqrt{3}\right)}}$

${\alpha }_1=\frac{1}{i}{\displaystyle {\int }_{L_1}\frac{\text{d}t}{2t-\left(1+i\sqrt{3}\right)}}=\frac{\pi }{3}$

${\text{Γ}}_{1*}\left(z\right)={\text{Γ}}_1\left(z\right)-\frac{\pi }{3}i$

${\text{Γ}}_{2*}\left(z\right)=\overline{{\text{Γ}}_2\left({\tau }_2\left(z\right)\right)}=\frac{1}{2}{\displaystyle {\int }_{L_2}\frac{\text{d}t}{t-z}}-\frac{1}{2}{\displaystyle {\int }_{L_2}\frac{\text{d}t}{t+1}}$

${\alpha }_2=\frac{1}{2i}{\displaystyle {\int }_{L_2}\frac{\text{d}t}{t+1}}=\frac{\pi }{3}$

${\text{Γ}}_{2*}\left(z\right)={\text{Γ}}_2\left(z\right)-\frac{\pi }{3}i$

${\text{Γ}}_{3*}\left(z\right)=\overline{{\text{Γ}}_3\left({\tau }_3\left(z\right)\right)}=\frac{1}{2}{\displaystyle {\int }_{L_3}\frac{\text{d}t}{t-z}}-{\displaystyle {\int }_{L_3}\frac{\text{d}t}{2t-\left(1-i\sqrt{3}\right)}}$

${\alpha }_3=\frac{1}{i}{\displaystyle {\int }_{L_3}\frac{\text{d}t}{2t-\left(1-i\sqrt{3}\right)}}=\frac{\pi }{3}$

${\text{Γ}}_{3*}\left(z\right)={\text{Γ}}_3\left(z\right)-\frac{\pi }{3}i$

$W_{*}\left(z\right)=\{\begin{array}{c}{\left(\overline{{\tau }_1\left(z\right)}-\bar{a}\right)}^{\frac{1}{2}}{\left(\overline{{\tau }_1\left(z\right)}-\bar{b}\right)}^{\frac{1}{2}}{\left(\overline{{\tau }_1\left(z\right)}-\bar{c}\right)}^{\frac{1}{2}}{\text{e}}^{-i\frac{\pi }{3}}{\text{e}}^{\text{Γ}\left(z\right)},z\in D_0\cup D_1\\ {\left(\overline{{\tau }_2\left(z\right)}-\bar{a}\right)}^{\frac{1}{2}}{\left(\overline{{\tau }_2\left(z\right)}-\bar{b}\right)}^{\frac{1}{2}}{\left(\overline{{\tau }_2\left(z\right)}-\bar{c}\right)}^{\frac{1}{2}}{\text{e}}^{-i\frac{\pi }{3}}{\text{e}}^{\text{Γ}\left(z\right)},z\in D_0\cup D_2\\ {\left(\overline{{\tau }_3\left(z\right)}-\bar{a}\right)}^{\frac{1}{2}}{\left(\overline{{\tau }_3\left(z\right)}-\bar{b}\right)}^{\frac{1}{2}}{\left(\overline{{\tau }_3\left(z\right)}-\bar{c}\right)}^{\frac{1}{2}}{\text{e}}^{-i\frac{\pi }{3}}{\text{e}}^{\text{Γ}\left(z\right)},z\in D_0\cup D_3\end{array}$

${\text{Ψ}}_{*}\left(z\right)=\overline{\text{Ψ}\left({\tau }_j\left(z\right)\right)}=-\frac{W_{*}\left(z\right)}{2\pi i}{\displaystyle {\int }_{L+\text{Σ}}\frac{2\tilde{f}\left(\tau \left(t^{+}\right)\right)}{\overline{W^{+}\left(t\right)}\left(\bar{t}-\overline{{\tau }_j\left(z\right)}\right)}\text{d}\bar{t}}+W_{*}\left(z\right)\left(\frac{\overline{{\lambda }_a}}{\left(\overline{{\tau }_j\left(z\right)}-\bar{a}\right)}+\frac{\overline{{\lambda }_a}}{\left(\overline{{\tau }_j\left(z\right)}-\bar{a}\right)}+\frac{\overline{{\lambda }_a}}{\left(\overline{{\tau }_j\left(z\right)}-\bar{a}\right)}\right)$

其中 $z\in D_0\cup D_j$，

那么

${\text{Ψ}}_0\left(z\right)=\frac{1}{2}\left[\text{Ψ}\left(z\right)+{\text{Ψ}}_{*}\left(z\right)\right]$

是问题(2)的解，且满足条件(4)。

接下来，我们来求解方程组(7)，令

$Q\left(z\right)={\text{e}}^{\text{Γ}(\; z\; )}$

易得

$\frac{Q^{+}\left(t\right)}{Q^{-}\left(t\right)}=-1,t\in L$

$Q^{+}\left(t\right)=Q^{-}\left(t\right)=1,t\in \text{Σ}$

方程组(7)两边同时除以 $Q^{+}\left(t\right)$，得

$\{\begin{array}{l}\frac{{\text{Ω}}_0^{+}\left(t\right)}{Q^{+}\left(t\right)}=\frac{{\text{Ω}}_1^{-}\left(t\right)}{Q^{-}\left(t\right)}+\frac{2\widetilde{\stackrel{˜}{f}}\left(t\right)}{Q^{+}\left(t\right)},t\in L_1\hfill \\ \frac{{\text{Ω}}_0^{+}\left(t\right)}{Q^{+}\left(t\right)}=\frac{{\text{Ω}}_2^{-}\left(t\right)}{Q^{-}\left(t\right)}+\frac{2\widetilde{\stackrel{˜}{f}}\left(t\right)}{Q^{+}\left(t\right)},t\in L_2\hfill \\ \frac{{\text{Ω}}_0^{+}\left(t\right)}{Q^{+}\left(t\right)}=\frac{{\text{Ω}}_3^{-}\left(t\right)}{Q^{-}\left(t\right)}+\frac{2\widetilde{\stackrel{˜}{f}}\left(t\right)}{Q^{+}\left(t\right)},t\in L_3\hfill \\ \frac{{\text{Ω}}_2^{+}\left(t\right)}{Q^{+}\left(t\right)}=\frac{{\text{Ω}}_1^{-}\left(t\right)}{Q^{-}\left(t\right)}+\frac{2\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right)}{Q^{+}\left(t\right)},t\in L_4\hfill \\ \frac{{\text{Ω}}_3^{+}\left(t\right)}{Q^{+}\left(t\right)}=\frac{{\text{Ω}}_2^{-}\left(t\right)}{Q^{-}\left(t\right)}+\frac{2\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right)}{Q^{+}\left(t\right)},t\in L_5\hfill \\ \frac{{\text{Ω}}_1^{+}\left(t\right)}{Q^{+}\left(t\right)}=\frac{{\text{Ω}}_3^{-}\left(t\right)}{Q^{-}\left(t\right)}+\frac{2\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\right)}{Q^{+}\left(t\right)},t\in L_6\hfill \end{array}$

因为

$\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(c\right)\right)=\frac{1}{2}\left[f\left({\tau }_2\left(c\right)\right)-f\left(\overline{{\tau }_2\left(c\right)}\right)\right]=\frac{1}{2}\left[f\left(c\right)-f\left(\bar{c}\right)\right]=\frac{1}{2}\left[f\left(c\right)-f\left(c\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)\right]=0$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(\infty \right)\right)=\frac{1}{2}\left[f\left({\tau }_2\left(\infty \right)\right)-f\left(\overline{{\tau }_2\left(\infty \right)}\right)\right]=\frac{1}{2}\left[f\left(b\right)-f\left(\bar{b}\right)\right]=\frac{1}{2}\left[f\left(b\right)-f\left(b\right)\right]=0$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(a\right)\right)=\frac{1}{2}\left[f\left({\tau }_3\left(a\right)\right)-f\left(\overline{{\tau }_3\left(a\right)}\right)\right]=\frac{1}{2}\left[f\left(a\right)-f\left(\bar{a}\right)\right]=\frac{1}{2}\left[f\left(a\right)-f\left(a\cdot {\mathrm{e}}^{-i\frac{2\pi }{3}}\right)\right]=0$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(\infty \right)\right)=\frac{1}{2}\left[f\left({\tau }_3\left(\infty \right)\right)-f\left(\overline{{\tau }_3\left(\infty \right)}\right)\right]=\frac{1}{2}\left[f\left(c\right)-f\left(\bar{c}\right)\right]=\frac{1}{2}\left[f\left(c\right)-f\left(c\cdot {\text{e}}^{i\frac{2\pi }{3}}\right)\right]=0$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(b\right)\right)=\frac{1}{2}\left[f\left({\tau }_1\left(b\right)\right)-f\left(\overline{{\tau }_1\left(b\right)}\right)\right]=\frac{1}{2}\left[f\left(b\right)-f\left(\bar{b}\right)\right]=\frac{1}{2}\left[f\left(b\right)-f\left(b\right)\right]=0$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(\infty \right)\right)=\frac{1}{2}\left[f\left({\tau }_1\left(\infty \right)\right)-f\left(\overline{{\tau }_1\left(\infty \right)}\right)\right]=\frac{1}{2}\left[f\left(a\right)-f\left(\bar{a}\right)\right]=\frac{1}{2}\left[f\left(a\right)-f\left(a\cdot {\text{e}}^{-i\frac{2\pi }{3}}\right)\right]=0$

所以，有

$\widetilde{\stackrel{˜}{f}}\left({\tau }_2\left(t\right)\right)\in H_{\rho }^{*}\left(c\right)\cap {\hat{H}}_0(\; L\; 4\; )$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_3\left(t\right)\right)\in H_{\rho }^{*}\left(a\right)\cap {\hat{H}}_0(\; L\; 5\; )$

$\widetilde{\stackrel{˜}{f}}\left({\tau }_1\left(t\right)\right)\in H_{\rho }^{*}\left(b\right)\cap {\hat{H}}_0(\; L\; 6\; )$

又

$Ord\left[\frac{\Omega }{Q},\infty \right]=-\frac{1}{2}$

故解为

$\frac{\text{Ω}\left(z\right)}{Q\left(z\right)}=\frac{1}{2\pi i}{\displaystyle {\int }_{L+\text{Σ}}\frac{2\widetilde{\stackrel{˜}{f}}\left(\tau \left(t^{+}\right)\right)}{Q^{+}\left(t\right)\left(t-z\right)}\text{d}t}+\frac{{\eta }_a}{\sqrt{z-a}}+\frac{{\eta }_b}{\sqrt{z-b}}+\frac{{\eta }_c}{\sqrt{z-c}}$

$\text{Ω}\left(z\right)=\frac{Q\left(z\right)}{2\pi i}{\displaystyle {\int }_{L+\text{Σ}}\frac{2\widetilde{\stackrel{˜}{f}}\left(\tau \left(t^{+}\right)\right)}{Q^{+}\left(t\right)\left(t-z\right)}\text{d}t}+Q\left(z\right)\left(\frac{{\eta }_a}{\sqrt{z-a}}+\frac{{\eta }_b}{\sqrt{z-b}}+\frac{{\eta }_c}{\sqrt{z-c}}\right)$

同样的，为了满足条件(6)，下面需构造 ${\text{Ω}}_{*}\left(z\right)$，通过计算可得

$Q_{*}\left(z\right)={\text{e}}^{-i\frac{\pi }{3}}Q(\; z\; )$

${\text{Ω}}_{*}\left(z\right)=-\frac{Q_{*}\left(z\right)}{2\pi i}{\displaystyle {\int }_{L+\text{Σ}}\frac{2\widetilde{\stackrel{˜}{f}}\left(\tau \left(t^{+}\right)\right)}{\overline{Q^{+}\left(t\right)}\left(\bar{t}-\overline{{\tau }_j\left(z\right)}\right)}\text{d}\bar{t}}+Q_{*}\left(z\right)\left(\frac{\overline{{\eta }_a}}{\sqrt{\overline{{\tau }_j\left(z\right)}-\bar{a}}}+\frac{\overline{{\eta }_b}}{\sqrt{\overline{{\tau }_j\left(z\right)}-\bar{b}}}\frac{\overline{{\eta }_c}}{\sqrt{\overline{{\tau }_j\left(z\right)}-\bar{c}}}\right)$

其中 $z\in D_0\cup D_j$，那么

${\text{Ω}}_0\left(z\right)=\frac{1}{2}\left[\text{Ω}\left(z\right)+{\text{Ω}}_{*}\left(z\right)\right]$

是问题(3)的解，且满足条件(6)。

5. 结论

最后，我们将问题(2)与问题(3)的解相加就得到了问题(1)的解，即

${\text{Φ}}_0={\text{Ψ}}_0\left(z\right)+{\text{Ω}}_0(\; z\; )$

致谢

感谢在论文撰写期间对我提供指导和帮助的老师，感谢各位审稿专家的辛勤工作和指导。