完全图去除路P₁₀的图谱特征

Spectral Characterization of the Complete Graph by Deleting P₁₀

摘要: 如果与图G同谱的所有图同构于图G，则称图G是由其图谱所决定的。设K_n\P_l是由完全图K_n去除图P_l的边所得到的子图，其中图P_l是长为l−1的路。Cámara和Haemers给出猜想1：对于任意的整数l(2≤l≤n)，K_n\P_l可由其邻接谱所决定。本文证明在l=10的情况下猜想1是正确的。

Abstract: A graph G is said to be determined by its spectrum if any graph having the same spectrum as G is isomorphic to G. Let K_n\P_l be the graph obtained from K_n by deleting edges of P_l, where P_l is a path of length l−1. Cámara and Haemers conjectured that K_n\P_l is determined by its adjacency spectrum for every (2≤l≤n). In this paper, we show that the conjecture is true for l=10.

1. 引言

本文所考虑的图都是无向、有限的简单图，即是不包含环和多重边的图。图谱中的一些符号和定义，请参阅文献 [1]。

设 $G=\left(V,E\right)$，其点集和边集分别记为 $V\left(G\right)=\left\{v_1,v_2,\cdots ,v_n\right\}$ 和 $E\left(G\right)=\left\{e_1,e_2,\cdots ,e_m\right\}$。设 $A\left(G\right)$ 是图G的(0, 1)邻接矩阵，图G的特征多项式记为 $P_G\left(\lambda \right)=\det \left(\lambda I-A\left(G\right)\right)$。图G的图谱包含了图G的所有特征值(包含重数)。如果两个图有一样的邻接谱，那么称这两个图同谱。如果任何与图G具有相同谱的图与图G同构，则称图G是由其谱所决定的(简称DS)。

图谱能够反映出图的一些有用的组合信息。图谱理论中的一个基本问题是“哪些图是DS？”。这个问题起源于化学，可以追溯到60多年前。而在近些年来，它受到了研究者的广泛关注。

然而，证明一个图是DS通常是一个非常困难的问题。到目前为止，很少有一类具有特殊结构的图被证明是DS。通常情况下，DS的图只包含有很少数的边，如T形树图 [2]、 $\infty$ 图 [3]、棒糖图 [4] 和 $\theta$ 图 [5] 等等。对于含有大量边的稠密图，这通常很难证明他们是DS。比如在文献 [6] 中，一条路的补图 ${\bar{P}}_n$ 被证明是DS，但是这个证明远比证明路 $P_n$ 是DS涉及的多。关于这一问题的更多背景可以参阅文献 [7] [8]。

在文献 [9] 中，Cámara和Haemers等人研究了在完全图下删除了其中的一些边后所得到的图是DS。 $P_l$ 为一条长为 $l-1$ 的路， $K_n$ 为 $n$ 阶的完全图。在 $K_n$ 中删除掉路 $P_l$ 的边所得到的图记为 $K_n\backslash P_l$。他们给出了以下的猜想：

猜想1 (Cámara和Haemers [9] )对于任意的整数 $l$ 满足 $0<l\le n$， $K_n\backslash P_l$ 是DS。

在文献 [9] 中，作者已经证明了在 $l\le 6$ 时猜想1是正确的。当 $n=l$ 时，也被证明了猜想1是正确的，这也是文献 [3] 中的主要结果。Mao，Cioabǎ和Wang在文献 [10] 中证明了当 $7\le l\le 9$ 时，猜想1是正确的。本文证明了在 $l=10$ 时，猜想1是正确，即：

定理1.1 当 $l=10$ 时，图 $K_n\backslash P_l$ 是DS。

在第二部分中，将给出一些重要的引理及其证明。在第三部分中给出了定理1.1的证明。本文总结和进一步的研究问题将会在第四部分给出。

2. 一些引理的介绍和证明

在这一部分中，将给出证明定理1.1所需要的一些引理。

引理2.1 (van Dam和Haemers [7] )图G的下列性质可以从邻接谱推导出来：

1) 顶点的数量；

2) 边的数量；

3) 固定长度的闭途径数量。

引理2.2 (Mao，Cioabǎ和Wang [11] )设 $N_G\left(H\right)$ 为在图G中与图H同构的子图(不一定是诱导)的数目， $N_G\left(i\right)$ 为图G中长为i的闭途径数目。设 ${N^{\prime }}_H\left(i\right)$ 为经过图H所有边且长为i的闭途径数目， $S_i\left(G\right)$ 为图G中所有连通子图H的集合，其中 ${N^{\prime }}_H\left(i\right)\ne 0$。这可以得出 $N_G\left(i\right)$ 为

$N_G\left(i\right)={\displaystyle \underset{H\in S_i\left(G\right)}{\sum }{N}_G\left(H\right){N^{\prime }}_H\left(i\right)}$。

引理2.3 (Omidi [11] )以下给出的是图G中长为2、3、4、5的闭途径的数目：

1) $N_G\left(2\right)=2m$， $N_G\left(3\right)=6N_G\left(K_3\right)$。

2) $N_G\left(4\right)=2m+4N_G\left(P_3\right)+8N_G\left(C_4\right)$； $N_G\left(5\right)=30N_G\left(K_3\right)+10N_G\left(C_5\right)+10N_G\left(G_a\right)$。

其中m为G的边数，图 $G_a$ 为圈图 $C_3$ 上任一个顶点加上一条边得到的图(见图2(a))。

引理2.4 (Cvetković，Doob和Sachs [1] )设图G中k-闭途径的数量为c，那么该数量可以由其邻接谱决定，即

$c={\displaystyle \sum {\lambda }_i^k}$。

设n阶图G的邻接谱为 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$，n阶图 $G^{\prime }$ 的邻接谱为 ${{\lambda }^{\prime }}_1\ge {{\lambda }^{\prime }}_2\ge \cdots \ge {{\lambda }^{\prime }}_n$。众所周知，若 ${\lambda }_i={{\lambda }^{\prime }}_i$， $i=1,2,\cdots ,n$，那么有

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\lambda }_i^k={\displaystyle \underset{i=1}{\overset{n}{\sum }}{{\lambda }^{\prime }}_i^k}}$。

也就是两个图的邻接谱相同，那么它们的各特征值的k次方和也相等，所以可以得到当

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\lambda }_i^k\ne {\displaystyle \underset{i=1}{\overset{n}{\sum }}{{\lambda }^{\prime }}_i^k}}$，

则有 ${\lambda }_i$ 与 ${{\lambda }^{\prime }}_i$ 不全相等， $i=1,2,\cdots ,n$。因此结合引理2.4，可以得到这么一个结论：当两个阶数相同的图的k-闭途径数量(k为正整数)不相同时，则它们的邻接谱不相同，即这两个图不同谱。引理2.5~2.7分别给出了当 $k=3,4,5$ 时，图G补图中k-闭途径数量的计算方法。

引理2.5 (Doob和Haemers [6] )设图G有n个顶点，m条边，t个子图 $C_3$ 和其度序列为 $d_1,d_2,\cdots ,d_n$。设 $\bar{t}$ 为图G补图的子图 $C_3$ 数量。则有

$\bar{t}=\left(\begin{array}{c}n\\ 3\end{array}\right)-\left(n-1\right)m+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{d}_i^2}-t$。

引理2.6 (Cámara和Haemers [9] )设图G有n个顶点，m条边，其补图4-闭途径的数量由图G的顶点和边的数量以及图G中同构于 $P_3$， $K_2\cup K_2$， $P_4$ 和 $C_4$ 的子图(不一定是诱导)数量所决定，分别用 $m_1$， $m_2$， $m_3$ 和 $m_4$ 表示，以及将图 $K_n$ 中4-闭途径的数量表示为 $W_n={\left(n-1\right)}^4+n-1$，则图G补图中的4-闭途径数量等于

$W_n-\left(8n^2-32n+34\right)m+\left(8n-20\right)m_1+16m_2-8m_3+8m_4$，

其中

$\begin{array}{l}n:=\left|V\left(G\right)\right|,m:=\left|E\left(G\right)\right|,m_1:=N_G\left(P_3\right),\\ m_2:=N_G\left(K_2\cup K_2\right),m_3:=N_G\left(P_4\right),m_4:=N_G\left(C_4\right).\end{array}$

研究长为5的闭途径的情况会更加的困难，将由以下引理提出。

引理2.7 (Mao，Cioabǎ和Wang [10] )设图G有n个顶点、m条边，其补图5-闭途径的数量由图G的顶点和边的数量，以及图G中同构于 $s_3$， $K_2\cup K_2$， $P_4$， $K_3$， $P_3\cup K_2$， $K_{1,3}$， $P_5$， $G_a$ 和 $C_5$ 的子图(不一定是诱导)数量所决定，分别用 $m_1$， $m_2$， $m_3$， $s_1$， $s_2$， $s_3$， $s_4$， $s_5$ 和 $s_6$ 表示，以及将图 $K_n$ 中5-闭途径的数量表示为 $W_n=30\left(\begin{array}{c}n\\ 3\end{array}\right)+120\left(\begin{array}{c}n\\ 5\end{array}\right)+30\left(n-3\right)\left(\begin{array}{c}n\\ 3\end{array}\right)$，则图G补图中的5-闭途径数量等于

$\begin{array}{l}{W}_n-\left(10n^3-50n^2+90n-60\right)m+\left(10n^2-20n\right)m_1+\left(40n-120\right)m_2\\ -\left(10n-20\right)m_3-\left(30n-60\right)s_1-20s_2-30s_3+10s_4+10s_5-10s_6\end{array}$。

其中

$\begin{array}{l}{s}_1:=N_G\left(K_3\right),s_2:=N_G\left(P_3\cup K_2\right),s_3:=N_G\left(K_{1,3}\right),\\ s_4:=N_G\left(P_5\right),s_5:=N{}_G\left(G_a\right),s_6:=N_G\left(C_5\right).\end{array}$

设H为有 $l-1$ 条边的简单图，下文将用 $m_1$， $m_2$， $m_3$， $s_1$， $s_2$， $s_3$， $s_4$， $s_5$ 和 $s_6$ 表示图 $P_l$ 中同构于 $P_3$， $K_2\cup K_2$， $P_4$， $C_4$， $K_3$， $P_3\cup K_2$， $K_{1,3}$， $P_5$， $G_a$ 和 $C_5$ 的子图数量，用 ${m^{\prime }}_1$， ${m^{\prime }}_2$， ${m^{\prime }}_3$， ${s^{\prime }}_1$， ${s^{\prime }}_2$， ${s^{\prime }}_3$， ${s^{\prime }}_4$， ${s^{\prime }}_5$ 和 ${s^{\prime }}_6$ 表示图H中同构于 $K_2\cup K_2$， $P_4$， $C_4$， $K_3$， $P_3\cup K_2$， $K_{1,3}$， $P_5$， $G_a$ 和 $C_5$ 的子图数量。

在给出和证明以下引理之前，先对几类特殊图进行符号的规定。符号 $T_{a,b,c}$ 表示为图1(a)所示的图例，其中a，b，c代表三条支路对应边的数量，且满足 $c\ge b\ge a\ge 1$，如图1(d)表示为 $T_{1,2,2}$。符号 $T_{a,b,c,d}$ 表示为图1(b)所示的图例，其中a，b，c，d代表四条支路对应边的数量，且满足 $d\ge c\ge b\ge a\ge 1$，如图1(e)表示为 $T_{1,2,2,3}$。符号 $Y_{a,b,c,d}$ 表示为图1(c)所示图例，其中a，b，c，d代表四个位置对应边的数量，且满足 $b\ge a\ge 1$， $d\ge c\ge 1$，如图1(f)表示为 $Y_{1,2,2,3}$。

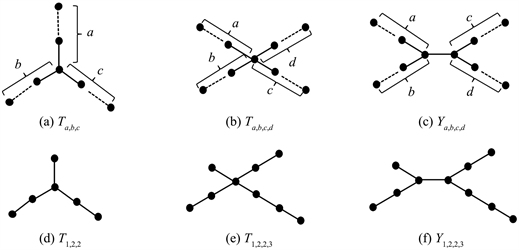
Figure 1. Special graphs of several types

图1. 几类特殊图

引理2.8 (Mao，Cioabǎ和Wang [10] )以下的三类图均与图 $K_n\backslash P_l$ 不同谱

1) 对于任意的整数 $l\ge 7$ 时，图 $K_n\backslash P_l$ 和 $K_n\backslash \left(C_4\cup P_{l-4}\right)$ 不同谱。

2) 对于任意的整数 $a\ge 1$， $b\ge 2$ 且满足 $3a+b=l$ 时，图 $K_n\backslash P_l$ 和 $K_n\backslash \left(a{K}_3\cup P_b\right)$ 不同谱。

3) 对于任意的整数 $a\ge 2$， $b\ge 1$， $c\ge 1$， $d\ge 1$ 且满足 $a+b+c+d=l\left(l\ge 6\right)$ 时，两类图 $K_n\backslash P_l$ 和 $K_n\backslash \left(P_a\cup T_{b,c,d}\right)$ 不同谱。

引理2.9 对于任意的整数 $a\ge 2$， $b\ge 1$， $c\ge 1$， $d\ge 1$ 且满足 $a+b+c+d=l-3\left(l\ge 10\right)$ 时，两类图 $K_n\backslash P_l$ 和 $K_n\backslash \left(P_a\cup T_{b,c,d}\cup K_{1，3}\right)$ 不同谱。

证明：图 $P_l$ 可以直接计算得出

$m_1=l-2,m_2=\frac{\left(l-2\right)\left(l-3\right)}{2},m_3=l-3,m_4=0.$

对于图 $P_a\cup T_{b,c,d}\cup K_{1，3}$，有

${m^{\prime }}_1=l-2,{m^{\prime }}_2=\frac{\left(l-2\right)\left(l-3\right)}{2}.$

由 $a+b+c+d=l-3$ 可得 $b+c+d<l-3$，又因为 ${m^{\prime }}_3\le b+c+d$，则

${m^{\prime }}_3<l-3,{m^{\prime }}_4=0.$

利用引理2.6，可以直接得出，图 $K_n\backslash P_l$ 和图 $K_n\backslash \left(P_a\cup T_{b,c,d}\cup K_{1，3}\right)$ 可以通过4-闭途径的数量来区分。£

引理2.10 对于任意的整数 $a\ge 1$， $4\le b\le 7$ 且满足 $2a+b=l-2\left(l\ge 9\right)$ 时，两类图 $K_n\backslash P_l$ 和 $K_n\backslash \left(a{P}_3\cup T_b\cup P_2\right)$ 不同谱，其中图 $T_b$ 表示为含有b条边的树。

证明：图 $P_l$ 可以直接计算得出

$m_1=l-2,m_2=\frac{\left(l-2\right)\left(l-3\right)}{2},m_3=l-3,m_4=0.$

对于图 $a{P}_3\cup T_4\cup P_2$， $a{P}_3\cup T_5\cup P_2$， $a{P}_3\cup T_6\cup P_2$ 和 $a{P}_3\cup T_7\cup P_2$，有

${m^{\prime }}_1=l-2,{m^{\prime }}_2=\frac{\left(l-2\right)\left(l-3\right)}{2},{m^{\prime }}_3\ne l-3,{m^{\prime }}_4=0.$

图 $P_l$ 和图 $a{P}_3\cup T_b\cup P_2$ 在n个顶点下的补图分别为图 $K_n\backslash P_l$ 和图 $K_n\backslash \left(a{P}_3\cup T_b\cup P_2\right)$，由引理2.6可知，这两类图可以通过4-闭途径的数量来区分，则不同谱。 £

引理2.11 (Mao，Cioabǎ和Wang [10] )设图 $K_n\backslash H$ 与图 $K_n\backslash P_l$ 同谱，则图H中子图 $C_3$ 数量 $t^{\prime }$ 为偶数。

引理2.12 (Mao，Cioabǎ和Wang [10] )设图 $K_n\backslash H$ 与图 $K_n\backslash P_l$ 同谱。那么图H有以下三个性质。

1) 除了 $C_3$ 和 $C_4$，图H的任何部分都不是圈。

2) 图H不包含两个不相交的圈 $C_k\cup C_s$。

3) 除了 $P_3$ 之外，图H包含两条长度不相等的路径。

3. 定理1.1的证明

设图 $G=P_l+\left(n-l\right)K_1$ 为 $K_n\backslash P_l$ 的补图，则图G有n个顶点， $l-1$ 条边，不含子图 $C_3$，并且其度序列为 $\left\{0^{n-l},1^2,2^{l-2}\right\}$。因此， $K_n\backslash P_l$ 中的子图 $C_3$ 数量 $\bar{t}$ 为

$\bar{t}=\left(\begin{array}{c}n\\ 3\end{array}\right)-\left(n-2\right)\left(l-1\right)+l-2=\left(\begin{array}{c}n\\ 3\end{array}\right)-\left(n-1\right)\left(l-1\right)+\frac{1}{2}\left(4l-6\right)$.

设图 $\Gamma =H+\left(n-\left|V\left(H\right)\right|\right)K_1$ 为 $K_n\backslash H$ 的补图，则其有n个顶点， $l-1$ 条边， $t^{\prime }$ 个子图 $C_3$，度序列为 $\left\{0^{n-{\displaystyle \sum {}_{i=1}^k{x}_i}},1^{x_1},2^{x_2},\cdots ,k^{x_k}\right\}$。那么图 $K_n\backslash H$ 中子图 $C_3$ 数量 ${\bar{t}}^{\prime }$ 为

${\bar{t}}^{\prime }=\left(\begin{array}{c}n\\ 3\end{array}\right)-\left(n-1\right)\left(l-1\right)+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{k}{\sum }}\left(i^2{x}_i\right)}-t^{\prime }$.

设图 $K_n\backslash H$ 和图 $K_n\backslash P_l$ 同谱，则两图含有相同数量的子图 $C_3$。而且由于删去了相同数量的边，那么删去的度数也是相等。因此有

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{k}{\sum }}i{x}_i}=2l-2,\\ {\displaystyle \underset{i=1}{\overset{k}{\sum }}{i}^2{x}_i=4l-6+2t^{\prime }.}\end{array}$ (1)

定理1.1的证明：当 $l=10$ 时，图H含有9条边，其最多含有7个子图 $C_3$，则有

$0\le t^{\prime }\le 7$. (2)

当 $l=10$， $t^{\prime }=7$ 时，有 ${\displaystyle \underset{i=1}{\overset{k}{\sum }}{i}^2{x}_i=4l-6+2t^{\prime }}=48$，当 $k=7$ 时不成立，所以k最大取6，则有

$0\le k\le 6$. (3)

对于 $x_i\left(i=1,2,\cdots ,6\right)$ 取值范围确定，当 $l=10$ 时，由

${\displaystyle \underset{i=1}{\overset{k}{\sum }}i{x}_i}=2l-2=18$

和

${\displaystyle \underset{i=1}{\overset{k}{\sum }}{i}^2{x}_i}=4l-6+2t^{\prime }=34+2t^{\prime }$,

可以得到

$0\le x_i\le \min \left\{\frac{18}{i},\frac{34+2t^{\prime }}{i^2}\right\}$. (4)

结合式子(1)-(4)，及Matlab计算，可以得到组合 $\left\{t^{\prime },x_1,x_2,x_3,x_4,x_5,x_6\right\}$ 的所有情况如下：

$\left\{0,2,8,0,0,0,0\right\},\left\{0,5,5,1,0,0,0\right\},\left\{0,8,2,2,0,0,0\right\},\left\{0,10,2,0,1,0,0\right\},\left\{1,0,9,0,0,0,0\right\},$

$\left\{1,3,6,1,0,0,0\right\},\left\{1,6,3,2,0,0,0\right\},\left\{1,8,3,0,1,0,0\right\},\left\{1,9,0,3,0,0,0\right\},\left\{1,11,0,1,1,0,0\right\},$

$\left\{2,1,7,1,0,0,0\right\},\left\{2,4,4,2,0,0,0\right\},\left\{2,6,4,0,1,0,0\right\},\left\{2,7,1,3,0,0,0\right\},\left\{2,9,1,1,1,0,0\right\},$

$\left\{2,13,0,0,0,1,0\right\},\left\{3,2,5,2,0,0,0\right\},\left\{3,4,5,0,1,0,0\right\},\left\{3,5,2,3,0,0,0\right\},\left\{3,7,2,1,1,0,0\right\},$

$\left\{3,11,1,0,0,1,0\right\},\left\{4,0,6,2,0,0,0\right\},\left\{4,2,6,0,1,0,0\right\},\left\{4,3,3,3,0,0,0\right\},\left\{4,5,3,1,1,0,0\right\},$

$\left\{4,6,0,4,0,0,0\right\},\left\{4,8,0,2,1,0,0\right\},\left\{4,9,2,0,0,1,0\right\},\left\{4,10,0,0,2,0,0\right\},\left\{5,0,7,0,1,0,0\right\},$

$\left\{5,1,4,3,0,0,0\right\},\left\{5,3,4,1,1,0,0\right\},\left\{5,4,1,4,0,0,0\right\},\left\{5,6,1,2,1,0,0\right\},\left\{5,7,3,0,0,1,0\right\},$

$\left\{5,8,1,0,2,0,0\right\},\left\{5,10,0,1,0,1,0\right\},\left\{6,1,5,1,1,0,0\right\},\left\{6,2,2,4,0,0,0\right\},\left\{6,4,2,2,1,0,0\right\},$

$\left\{6,5,4,0,0,1,0\right\},\left\{6,6,2,0,2,0,0\right\},\left\{6,8,1,1,0,1,0\right\},\left\{7,0,3,4,0,0,0\right\},\left\{7,2,3,2,1,0,0\right\},$

$\left\{7,3,0,5,0,0,0\right\},\left\{7,3,5,0,0,1,0\right\},\left\{7,4,3,0,2,0,0\right\},\left\{7,5,0,3,1,0,0\right\},\left\{7,6,2,1,0,1,0\right\},$

$\left\{7,7,0,1,2,0,0\right\},\left\{7,12,0,0,0,0,1\right\}.$

有这样一组参数 $\left\{t^{\prime },x_1,x_2,x_3,x_4,x_5,x_6\right\}$，如果存在一个与该参数相同的图，那么称这组参数为该图的图解。实际上，并不是所有的这些参数组合都是图解，有部分是不符合图条件要求的。并且这些有效的图解中可能存在多个图的表示。如表1所示，这里只给出有效图解的组合和其相对应的图(表1中相关的子图见图2)。

根据引理2.8~2.12，除了图 $Y_{1,1,1,1}\cup 2P_3$、 $2T_{1,1,2}\cup P_2$、和 $G_d\cup 2P_3$ 以外，这里剩余的所有图的 $K_n\backslash H$ 都与 $K_n\backslash P_{10}$ 不同谱。接下来将计算在这三个图中4-闭途径的数量，并在表2中给出它们各子图的数量。

对于图 $P_{10}$，直接计算得

$m_1=l-2=8,m_2=\frac{\left(l-2\right)\left(l-3\right)}{2}=28,m_3=l-3=7,m_4=0.$

Table 1. Complements of all possible K n   \ H of the same spectrum as K n   \ P 10

表1. 所有可能与 $K_n\backslash P_{10}$ 同谱的 $K_n\backslash H$ 的补图

Table 2. The number of related subgraphs of H

表2. 图H的相关子图数量

通过表2中图H与图 $P_{10}$ 的各子图数量对比，以及引理2.6，则这三个图作为H时，图 $K_n\backslash H$ 与图 $K_n\backslash P_{10}$ 有不同数量的4-闭途径，因此它们不同谱。综上所述，证得图 $K_n\backslash P_{10}$ 是DS。定理1.1得证。 £

Figure 2. Some related subgraphs

图2. 文中涉及到的一些相关子图

4. 小结

在本文中，主要利用图 $K_n\backslash P_l$ 的邻接谱性质，通过对与图 $K_n\backslash P_l$ 可能同谱的图做详细的分类，并且计算图的4-闭途径和5-闭途径的数量是否相同，来得到他们是否同谱，从而证明在l取值较小的情况下图 $K_n\backslash P_l$ 是DS。但在取较大值的l时，与 $K_n\backslash P_l$ 可能同谱的图的详细分类会非常的复杂和繁琐，运用以上的方法是不理想的。因此，要证明猜想1在一般情况是正确，需要新的方法和工具。

致谢

感谢审稿人对本文提出的修改意见，并感谢游志福教授在本篇文章的写作过程中给予指导。