1. 引言
目前,机械化、自动化是航空航天铆接装配制造技术发展的必然趋势,自动化铆接不仅大大提高了生产效率,减轻工人的劳动强度,而且保证了产品质量的一致性 [1] [2]。有头铆钉手工铆接工艺技术成熟,但与自动钻铆设备匹配性差,当送钉杆直径较大时,会出现送钉杆与桁条立筋干涉的现象,根本原因是铆钉钉头尺寸大于钉杆。无头铆钉的出现恰可解决这一难题,无头铆钉是一种没有铆钉头的实心圆杆干涉铆钉,它具有以下优点:1) 铆接后沿铆钉杆全长可形成较均匀的干涉配合,成倍地提高连接结构的疲劳寿命;2) 采用无头铆钉干涉配合的铆接,能够可靠地保证铆钉自身的密封性 [3]。
无头铆钉一般用于自动钻铆设备,当装配件下架后往往还需要二次上架补铆一定数量的铆钉。尽管补铆的铆钉数量很少,但二次上数控托架、定位等却要花费很多时间,影响整个自动钻铆设备的高效利用,从而增加产品制造成本。因此有必要展开无头铆钉架下铆接的工艺参数研究。本文以ABAQUS软件为基础,分析无头铆钉铆接变形的过程,以双面鼓形镦头为例,进行了以下分析:不同铆钉长度对镦头尺寸和干涉量的影响,不同钉孔直径对干涉量的影响,有头铆钉和无头铆钉的性能对比。
2. 仿真模型的建立
铆接过程中铆钉各点位移、应变和应力对称于铆钉轴线,而夹层材料在铆接过程中塑性影响区材料各点位移、应变和应力也对称于铆钉的中心轴,因此在数值模拟中的集合模型采用轴对称模型。模型中只取中轴面的1/2。铆钉和夹层网格均采用轴对称应力单元CAX4R,有限元模型及网格划分如图1所示。

Figure 1. Finite element model and meshing
图1. 有限元模型及网格划分
2.1. 材料选型及参数
本文仿真选用的无头铆钉材料为2A10,T4状态,其弹性模量为71 GPa,泊松比0.31,密度2800 Kg/m3,其应力应变关系如图2所示。铆接件材料选2A12,T4状态,其弹性模量为72 GPa,泊松比0.31,密度2800 Kg/m3 [4]。铆接工具铆接时变形较小,故仿真中以刚性平面代替。
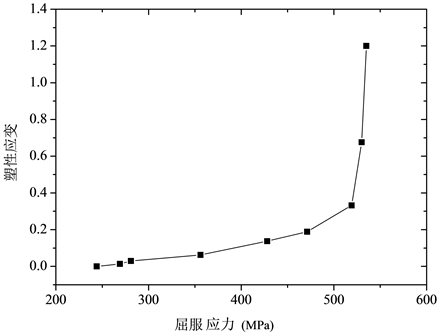
Figure 2. Stress-strain diagram of 2A12 aluminum alloy
图2. 2A10铝合金材料应力–应变关系图
2.2. 接触和摩擦处理
相互作用的切向行为为罚函数,摩擦系数为0.17。法向行为为硬接触,为分析铆接后的残余应力,允许接触后分离。
2.3. 载荷和边界条件
对上下方刚性平面施加完整约束,模拟铆枪枪头和顶铁(或枪头)实际工况;由于整个模型为轴对称建模,所以在中轴线处对模型的横向位移进行约束。
铆接成形时间较短,且整个过程中冲击力变化起伏较大,以冲击力的方式施加载荷显然不能实现,所以对上下方刚性平面施加纵向的位移约束,模拟对铆钉的位移载荷。
3. 铆接变形过程模拟分析
按铆钉镦粗情况将铆接变形分五个阶段 [5] [6]
1) 初始放置阶段:将铆钉放置在预先开有孔的被连接件中,用专用工装保证两边的外伸量一致,如图3(a)所示。
2) 铆钉压缩阶段:从压铆头和铆钉接触开始,钉杆逐渐被镦粗,随着压铆头位移的增大,压铆力逐渐增大,铆钉的钉杆从弹性变形逐渐转换到塑性变形。这一阶段中只有铆钉的挤压变形,铆钉和钉孔之间还未接触,如图3(b)所示。
3) 钉孔填充阶段:压铆头继续移动,铆钉和钉孔开始接触,接触面积逐渐增大,铆钉的径向变形受到约束,对被铆接件形成横向挤压,这一阶段铆钉中金属变形以向下流动为主,直到钉杆在整个钉孔轴向完全填充,如图3(c)所示。
4) 镦头成形阶段:在径向成形进一步受到约束时,在被连接件外的铆钉端开始局部镦粗,镦粗部分和被连接件表面相接触,在两者表面的摩擦力作用下,铆钉中金属流动方向由向下流动逐渐改变为向侧向流动,镦头逐渐增大,对被连接件形成轴向挤压,直到压铆头运动到指定的行程后,形成完整镦头,如图3(d)所示。
5) 弹性回复阶段:在压铆头运动到指定的行程后开始逐渐远离墩头,镦头和压铆头逐渐分离。铆钉和被铆接板上的弹性变形逐渐回复,如图3(e)所示。
4. 无头铆钉干涉量影响因素分析
4.1. 干涉量计算方法
铆接干涉量有绝对干涉量和相对干涉量两种,绝对干涉量为铆后孔径或钉径减去铆前直径,相对干涉量还要除以铆前直径,相对干涉量更能反应干涉情况。计算干涉量,在杆径位置取四点求平均值,取点如图4所示。
相对干涉量计算公式为:
式中,D0—铆前直径,D—铆后孔径或钉径。
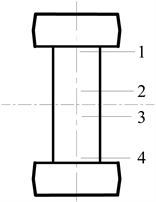
Figure 4. Schematic diagram of calculation value of interference quantity
图4. 干涉量计算取值示意图
4.2. 铆钉长度对铆接成形的影响
航空航天领用对产品重量要求严格,一个铆接成形的壳体上会有成千上万颗铆钉,铆钉长度较长则会使壳段产品重量增加,铆钉长度较短则连接强度不够 [4]。本文的研究以常用的Φ4铆钉为例,钉孔直径为Φ4.1,连接件的夹层总厚6 mm,选择铆钉长度为15 mm、16 mm、17 mm、18 mm来分析,保证成形时间一致,查看铆接成形后的镦头直径、镦头高度和干涉量。仿真结果如表1、图5所示。

Table 1. Data sheet of rivet interference of difference lengths
表1. 不同铆钉长度干涉量数据表
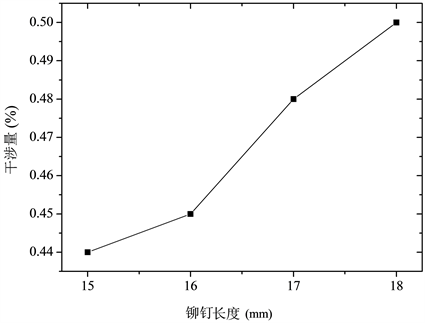
Figure 5. River length interference diagram
图5. 铆钉长度干涉量关系图
由仿真结果知,随着铆钉长度的增加,干涉量逐渐增大。因仿真中设置不同长度的铆钉成形后的镦头高度基本一致,故铆钉长度越长,成形后的铆钉镦头直径越大,镦头直径大,说明在镦头成形阶段铆钉镦粗现象明显,铆钉对连接件的轴向及侧向挤压越明显,干涉量就大。由测量的四处直径知,离镦头越近的干涉量越大,此处的镦粗现象更明显。
4.3. 钉孔直径对铆接成形的影响
铆钉直径4 mm,铆钉长度16 mm,设置不同的钉孔直径Φ4.1、Φ4.2、Φ4.3,铆钉在钉孔直径成形过程中,由于钉杆存在镦粗的情况,钉孔直径的增大使得钉杆镦粗阶段时间延长、铆钉对连接件的轴向及侧向挤压越小,使得上下干涉量相较于小钉孔更加均匀,但相对干涉量逐渐减小,如表2所示。

Table 2. Interference data table of difference nail hole diameters
表2. 不同钉孔直径干涉量数据表
5. 有头铆钉和无头铆钉的对比
航空航天常用铆钉为半圆头铆钉、90˚或者120˚沉头铆钉,为分析有头铆钉和无头铆钉的铆接性能优劣,以直径Φ4为例做仿真试验。设置钉孔直径Φ4.1,连接件的夹层总厚6 mm。选用的无头铆钉长度为16 mm,有头铆钉的长度为11 mm,保证铆钉外伸量一致。得到的仿真数据表如表3、图6所示。

Table 3. Interference data sheet for ordinary and headless rivets
表3. 有头铆钉和无头铆钉干涉量数据表
 (a)
(a)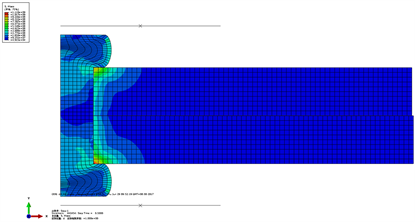 (b)
(b)
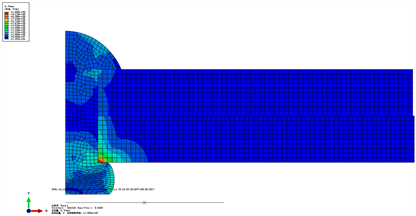
Figure 6. Stress nephogram after rivet forming. (a) ordinary rivets; (b) headless rivets
图6. 铆接成形后的应力云图。(a) 普通铆钉;(b) 无头铆钉
在初始放置阶段,有头铆钉的镦头侧外伸量为3 mm,无头铆钉的两侧外伸量均为3 mm。在铆钉压缩阶段,有头铆钉进行单侧压缩,无头铆钉是双侧压缩。在钉孔填充阶段,有头铆钉对被铆接件事单向横向挤压,无头铆钉对被铆接件是双向横向挤压。在镦头成形阶段,有头铆钉单侧形成双面镦头,无头铆钉双侧形成双面鼓形镦头。
无头铆钉因双面挤压,故靠近镦头两侧干涉量均较大。有头铆钉单面成形镦头,离镦头越远,干涉量越小,整体干涉量均值小于无头铆钉。同样外伸量下,有头铆钉的镦头直径小于无头铆钉,因有头铆钉要填充两个连接件的钉孔间隙,故在无头铆钉的外伸量及长度选择时,可适当小于有头铆钉。由应力云图可知,应力最大均集中在镦头附近,无头铆钉的应力分布相比有头铆钉更均匀。
6. 结论
通过ABAQUS仿真模型,分析铆接成形时金属流动情况,铆钉先进行径向向下镦粗,直至与钉孔接触开始横向挤压,然后铆钉侧向流动形成镦头。铆钉越长,镦粗现象越明显,干涉量越大。钉孔直径的增大,钉杆镦粗时间长,干涉量有所减小。相同条件下无头铆钉的干涉量大于有头铆钉。
本文仅定性分析参数不同干涉量变化趋势,铆接真实干涉量还需做试验研究,实际铆接有很多因素不可控,如不能保证两边伸出量完全对称,需进一步进行试验研究来验证仿真模型、探究铆接规律。
参考文献