摘要:
本文主要研究城市的公交乘车方案问题,对于乘车方案,我们以最少换乘次数为主要目标,以最少乘车时间为第二目标,结合公路交通量对道路通行时间的影响,即路阻函数,选择出一个符合要求的最优公交乘车方案;对于方案的选择,我们采用对公交线路进行搜寻的办法,寻找经过起点与终点的公交线路的集合,并根据直达、一次换乘、两次换乘对这两个集合分别进行搜寻,得到可行的方案后计算每个方案花费的时间并进行比较,从而选出最佳的乘车方案。最后,我们以湖南省长沙市为例,结合不同时间段的公路交通量计算出5组出行线路的最佳乘车方案。
Abstract:
This article mainly studies the problem of the bus ride schemes in a certain city. For riding schemes, we take the least transfer as the main goal, and the minimum time as the second goal, combined with the impact of highway traffic flow on road transit time—BPR (Bureau of Public Road) function, then select the optimal riding scheme that meets the requirements; for the choice of the strategy, we use the method of searching for bus routes, looking for the collection of bus routes passing through the starting point and ending point respectively. Then according to the direct, one-time transfer and two transfers, the two sets are searched separately, and the feasible plans are calcu-lated and the time spent on each plan is compared, so as to select the best riding scheme. Finally, we take Changsha City, Hunan Province as an example, combined with road traffic flow at different time periods to calculate the optimal riding scheme for 5 groups of travel routes.
1. 引言
随着经济社会的发展,由人类活动所排放的温室气体日益增加,造成温室效应,使得全球气候变暖。世界各国正面临着前所未有的气候问题与挑战。中国作为世界上最大的发展中国家,每年温室气体排放量约占全世界排放总量的15%。我国已成为全球温室气体排放总量最大的国家,并且短期内碳排放绝对量继续增长的趋势不会改变,因此承受着巨大的国际减排压力。并且随着十四五规划“碳中和”的提出,减少碳排放已经成为我国一个重要的工作目标。
随着汽车的普及,其过量无节制的使用是造成碳排放增加的主要原因之一。减少碳排放,实现碳中和,一方面需要合理规划小型汽车的使用,另一方面也要鼓励和倡导人们选择使用绿色能源的公共交通出行方式。在推动城市经济社会可持续发展过程中,如何完善公共交通管理制度,提供更加便捷、快捷和经济的公共交通出行方式,普及使用绿色能源的公交,这些都是我们值得探讨的问题,这也直接影响着人们是否选择公共交通出行方式。
虽然公交有着这样的优势,但在出行的便捷性和速度上却不如私家车,因此如何选择一条合适的公交线路成为一个需要解决的问题。城市交通管理要比航空和铁路运输管理复杂得多,因为航班、列车的运行时间、出发地、终点、甚至当前位置都可以知道,而城市交通,被管理的目标有各种机动车、非机动车、还有行人,关键是他们个体的出行精确数据无法得到,这就给准确的数值模拟带来了很大的困难。本项目的研究主要是基于已有的公交线路和交通量来选择一条符合人们要求的路线,重点探索缩短人们公交出行的时间的途径,本项目的研究对人们使用公共交通具有推动作用。
2. 问题分析
想要寻求一条乘车时间最短的乘车方案往往采用的是Dijkstra标号法 [1],该算法是使用最为广泛的解决有向图的最短路径的算法,该算法以每个公交站作为节点,求出从起点到终点的最短路径,如果在乘车方案中使用这个算法将会出现换乘多次才能到达终点的情况,虽然求出了最短路径,但不符合人们的乘车心理,因此这种方法不可取;同时这种方法不适合处理节点多的问题,Dijkstra标号法的时间复杂度是,对于长沙市有5000左右个节点,计算出结果往往需要花费很多时间,而公交线路只有419条。本文优先考虑换乘次数,以最少的换乘次数为第一目标,以最少乘车时间为第二目标,同时结合交通量对道路通行时间的影响建立一个数据量少、计算速度快的最优乘车方案算法。
3. 模型建立与求解
为了模型求解的方便,本文对模型做出以下假设:
1) 每条公交线路上相邻公交车站的自由行驶时间相同,为
;
2) 两辆公交车的平均换乘时间为
;
3) 公交车的实际路段通行时间只与当前路段的通行量有关;
4) 将所有的公交线路视为单向的,即使是双向也视为两条单向,且无环行线。
下面引入如下记号:
表示第
条公交线路,
表示第
条公交线的第
个公交站,
表示第
条公交线的第
个公交站到第
个公交站的实际道路通行时间,
和
分别表示第
条公交线的第
个公交站到第
个公交站的路段的道路通行量和实际通行能力,经过某公交站
的所有公交线路的集合记为
,所有公交站的集合记为
。
根据路阻函数,道路的实际通行时间与道路的自由通行时间存在以下的函数关系 [2]:
其中
和
为模型参数,本文中取
。
算法如下:
对于
,找到相应的
和
3.1. 直达车算法
若
,则说明节点
与
之间存在直达线路,对
,找出节点
与
在线路
中相对应的节点是
和
,如图1。
若
,说明是反方向的线路,此时线路
不可取;若
,此时线路
就是可行的线路,并计算乘坐此线路需要花费的时间
找出这些线路中时间花费最少的
,则最佳乘车方案即为线路
。
3.2. 一次换乘算法
若
,则说明节点
与
之间不存在直达线路,此时考虑一次换乘的方案,
,找出
在
中对应的节点是
,对于经过
之后的节点
的线路集合
,即
若
,说明此时存在一次换乘的方案,如图2,按照上述的直达车算法寻找可行的公交线路,同时计算相应趁车花费的时间加上换乘需要的时间即可得出总花费的时间,再对可行方案的集合进行比较进一步确定花费时间最少的方案。
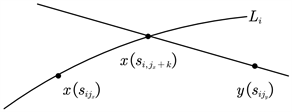
Figure 2. Map of public traffic transfer
图2. 一次换乘示意图
3.3. 两次换乘算法
若
,说明此时不存在一次换乘的方案,此时考虑两次换乘,
,找出
在
中对应的节点是
,对于经过
之前的节点
的线路集合
,即
若
,说明存在换乘两次的方案,同样按照直达车的算法找出相应的乘车路线并同时计算相应趁车花费的时间加上两次换乘需要的时间即可得出总花费的时间,再对可行方案的集合进行比较进一步确定花费时间最少的方案。
4. 实际应用——以湖南省长沙市公交线路为例
对于长沙市的公交线路网,我们得到了419条公交线路及其上的站点信息,并对公交线路进行编号,按照以上说明的算法计算下列组站点在自由通行时的最优乘车方案如下(表1,表2)。

Table 1. Optimal scheme of one public traffic transfer
表1. 一次换乘最优方案

Table 2. Optimal scheme of two public traffic transfer
表2. 二次换乘最优方案
基金项目
2020年湖南省普通高等学校教学改革研究项目“数学与应用数学专业‘二三三四’人才培养模式的研究与实践”(编号:HNJG-2020-0276)。长沙理工大学大学生创新创业训练计划项目。