1. 引言
股票市场作为一国经济的晴雨表,其波动往往引起公众的广泛关注。而股票市场的波动性一直是统计研究的热点问题,加之2020年爆发的新型冠状病毒肺炎疫情,医疗器械板块的股价波动引起本文的关注。本文选取了医疗器械板块的股票作为研究对象,对其价格进行估计预测。股市是一个复杂的非线性系统,股票价格涉及许多不确定因素,且各个因素之间的相关关系错综复杂 [1]。传统计量经济学模型认为股价波动完全是随机的,但大量事实表明,股价波动存在某种规律性 [2]。我们可以将股市看作确定的非线性动力系统。股票价格作为一种常见的金融时间序列,其波动影响因子之间关系呈现复杂的特征,基于传统的计量经济假设下的GARCH模型只能捕捉到序列之间的线性关系,而忽略了序列中复杂的非线性特征,从而导致估计结果的偏差过大,为此本文引进机器学习中的神经网络对股票价格进行预测分析,发现神经网络对于股票价格的估计预测优于传统的GARCH模型,进而对投资者而言,能够更好的规避股市风险、制定合理的投资计划 [3]。
传统的股票时间序列预测模型是通过建立在时间序列模型之间具有弱相关关系的基础上建立的,以此来预测未来的股票价格 [4]。1982年,美国经济学家Engle针对金融时间序列首次提出了ARCH模型(自回归条件异方差模型),由于ARCH模型对一个序列的预测存在滞后阶数多,参数难以估计的缺点,在此基础上,Bolerslev提出了改进的ARCH模型,GARCH (广义自回归条件异方差模型),使用较低的滞后阶数就可以很好的展现出收益的波动率特征,从而弥补了ARCH模型在参数估计方面的缺点,进一步刻画金融时间序列的波动性特征 [1]。但是由于股票市场往往存在杠杆效应,即负面影响的冲击往往大于正面影响带来的冲击,传统的GARCH模型对于股票收益率序列的非对称性无法做到较好的捕捉,在此基础上,Nelson (1991)提出了对GARCH模型的改进EGARCH (指数自回归条件异方差模型),能够更好的刻画股票收益率的非对称性。
基于ARMA-GARCH模型对股票时间序列进行建模分析预测时,往往会出现预测结果不理想、精确度不高等问题 [5]。1990年,Varies、Versino首次把人工神经网络用于经济研究领域,对金融时间序列问题进行建模,这也引起本文的兴趣。用人工神经网络对医疗器械板块股票重新进行估计,实证分析发现相比较于计量经济学分析方法,人工神经网络具有更强的预测分析能力 [6]。Weigend等把神经网络用于研究太阳黑子的年平均活动情况,通过与回归方法的比较表明神经网络的预测优于统计预测。20世纪90年代以来,利用神经网络对股票价格预测方法就已经层出不穷,本文便使用了前向传播网络与GARCH模型分别对股票价格和收益率进行对比(对于GARCH模型预测出的对数收益率,本文将其转化成价格进行比较),发现神经网络在预测方面的确优于传统的模型 [7] [8] [9]。
2. 模型简述
2.1. ARMA模型
将任意一个时间序列经过预处理后,变成蕴含相关信息的平稳非白噪声序列,这时就可以用ARMA模型对此序列进行拟合,提取出关键信息。ARMA为自回归移动平均模型,可细分为AR模型,MA模型,和ARMA模型三大类,分别具有如下形式:
(1)
(2)
(3)
AR模型有偏自相关函数截尾的性质;MA模型有相关函数截尾的性质。有些因果线性时间序列有与AR和MA类似的表现,但是不能在低阶实现偏自相关函数截尾或者相关函数截尾。ARMA模型结合了AR和MA模型,在对数据拟合优度相近的情况下往往可以得到更简单的模型,而且不要求偏自相关函数截尾也不要求相关函数截尾。在式(3)中,
为独立同分布零均值白噪声序列,
与
独立。
称为特征多项式,特征多项式的根都在单位圆外,这个条件称为可逆条件。两个多项式没有公共根,否则统一模型可能会有不同的表示。
2.2. ARCH模型
在经济研究领域,经常发现有在消除确定性非平稳因素后,残差序列大部分时段是平稳的但在某一时段会有较大波动,某一时段会有较小波动,具有异方差波动特征,存在波动聚集的现象,不满足时间序列建模的同方差的假设,也就无法使用时间序列的分析方法分析问题,于是Engle (1982)提出了ARCH模型(自回归条件异方差模型),这是对波动率定义为条件标准差,第一次提出的波动率的理论模型,基本思想是:1) 资产收益率的扰动序列
是前后不相关的,但是前后不独立;2)
的不独立性,描述为
可以用
的滞后值的线性组合表示。
具体的ARCH (m)模型为:
(4)
(5)
其中
是零均值单位方差的独立同分布的白噪声,
。
还需要满足一些条件使得
有限,类似于
序列的平稳性的特征根条件。
ARCH模型实质就是构造一个模型,利用历史波动信息,得到条件方差信息,采取自回归形式刻画波动的变化。如下式所述:
(6)
对于一个时间序列来说,不同时刻包含不同历史信息,所以有不同的条件方差,用ARCH模型可以很好的刻画时间序列的这种波动特征。
2.3. GARCH模型
ARCH模型实质是用残差平方序列的移动平均来拟合当期的异方差数值,通常只适用于短期自相关过程,对于有长期自相关性的残差序列(ARCH模型具有较高的滞后阶数),使用ARCH模型会增加它待估参数的难度和估计精确度,于是引入GARCH (广义自回归条件异方差)模型。对于一个对数收益率序列
,令
为其新息序列,称
服从
模型,如果
满足:
(7)
其中为零均值单位方差的独立同分布白噪声序列,
,
,
,
,最后一个条件是用来保证模型的
的无条件方差有限且不变,而条件方差
可以随时间t的变化而变化。
2.4. EGARCH模型
由于GARCH模型在处理时间序列中没有考虑到股票收益率的非对称效应,Christie (1982)的研究认为,当股票价格下降时,资本结构当中附加在债务上的权重增加,如果债务权重增加的信息泄漏以后,资产持有者和购买者就会产生未来资产收益率将导致更高波动性的预期,从而导致该资产的股票价格波动。因此,对于股价反向冲击所产生的波动性,大于等量正向冲击产生的波动性,这种“利空消息”作用大于“利好消息”作用的非对称性。为了克服GARCH模型处理时间序列上的问题,Nelson (1991)考虑了加权的新息,由此提出了EGARCH或指数(Exponential) GARCH模型。
(8)
其中
和
是实常数。
和
都分别是零均值独立同分布白噪声,分别为连续分布,易知
。
(9)
根据上式可见
的分布是非对称的。当
时,
模型可以用滞后算子的形式写成:
(10)
其中
为常数,其中B是滞后算子,多项式
和
的根都在单位圆外且两个多项式没有公因子。记
,则上式给出的
为一个平稳线性
序列,以
零均值独立同分布白噪声
为新息;但是,
通过
,序列依赖。原始的GARCH模型
的
直接依赖于
的,
对
影响相同。易知,
。EGARCH与GARCH模型的区别还有:1) 使用条件方差的对数建模,因为对数值可正可负,这就取消了GARCH模型对系数必须非负的
限制;2)
的使用使得波动率对
的依赖关系与
的正负号有关,可以用来描述正负收益率的不同的影响。
此外对于序列
拟合GARCH模型有一个基本要求即需为零均值,纯随机,异方差序列。但有时
不能充分提取原序列相关信息,
就不具有纯随机性。这时需要考虑AR-GARCH模型,具有如下形式:
(11)
这就是先对
拟合自回归模型,再考虑
的方差齐性,如具有异方差,对此拟合GARCH模型,称为AR(m)-GARCH(p, q)模型。
2.5. 神经网络模型
人工神经网络(Artificial Neural Network, ANN)简称神经网络(ANN),是基于生物学中神经网的基本原理,在理解和抽象了人脑结构和外界刺激响应机制后,以网络拓扑知识为理论基础,模拟人脑的神经系统对复杂信息的处理机制的一种数学模型。该模型具有高度的非线性,能够进行复杂的逻辑操作和非线性关系实现的系统。ANN是由大量处理单元经广泛互连而组成的人工网络,用来模拟脑神经系统的结构和功能。这些处理单元我们称作人工神经元。人工神经网络便可看成是以人工神经元为节点,用有向加权弧连接起来的有向图。在有向图中,人工神经元就是对生物神经元的模拟,而有向弧则是轴突—突触—树突对的模拟。
机器学习中的神经网络结构由输入层、隐含层、输出层组成。假设有N个任意样本集
,
其中
(12)
通过神经网络可以自动找寻x与y之间的非线性映射关系。对于具有L个隐含结点的单隐层神经网络的输出
可以表示为
(13)
式(13)中,g为激活函数,一般为σ函数。
为第i个隐层单元的输入权重,i为第i个隐层单元的偏置,
为第i个隐层单元的输出权重。
为神经网络的输出值。上式的矩阵形式为
(14)
其中,
单隐层神经网络对输入的N个样本集
进行自我学习,通过最小化输出值与是机智的误差平方和估计参数
,得到x与y之间的非线性映射关系:
(15)
式(11)等价于最小化损失函数:
(16)
式(15)无解析解,采用梯度下降法可得到模型参数估计。
3. GARCH模型的建立
3.1. 样本选取及处理
本文选取2019年12月2日到2020年3月16日我国医疗器械板块股票的相关数据,进行筛选得出医疗器械板块股票的日收盘价P,数据来源于聚宽量化分析网站。分别在GARCH模型与神经网络模型中进行预测分析。在神经网络模型中将2019年12月2日至2020年2月15日的数据作为训练数据,2020年2月17日至2020年3月16日数据为检验数据,从而进行日收盘价的的预测。在GARCH模型中将2019年12月5日至2020年3月16日的数据作为实验数据,从而进行收益率的预测。运用R统计建模软件,对最终筛选出的日收盘价P做时间序列图,见图1。由时序图可以看出,医疗器械板块股票日收盘价随着时间的波动而波动性,是一个非平稳的时间序列。对其进行了ADF检验,检验的P值为0.6021,大于0.05的显著性水平,我们有理由不拒绝原假设,即序列是非平稳的,这与时序图展示的结果是一致的。而在建立时间序列模型时,假设序列是平稳的,所以需要对原始数据进行差分处理使其达到建模的要求。又加之在研究金融时间序列时,人们往往关注的是收益率而并非收盘价,所以我们考虑对医疗器械板块股票日收盘价取对数,同时做差分转化成对数收益率。再对新建立的对数收益率进行平稳性检验,看其是否符合建模的要求。对数收益率的公式如下:
其中,
表示时刻t的收盘价,
表示t − 1时刻的收盘价,DR表示对数收益率。
对新建立的对数收益率序列做时间序列图,结果如图1所示。
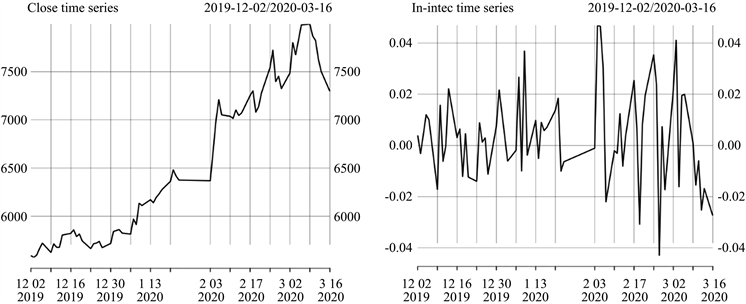
Figure 1. Medical devices sector time-series chart and yield sequence chart
图1. 医疗器械板块时序图与收益率序列图
由对数收益率的时序图可以看出序列出现了许多异常的峰值。当新冠疫情爆发之后的波动十分剧烈,也表现出了明显的波动聚集性,认为使用GARCH模型来刻画对数收益率的波动性是合理的。为验证可视化结果的真实性,即其是否真正处于平稳状态,同样做了ADF检验,检验的P值为0.09756,发现其并非为平稳时间序列,因此对对数收益率进行一阶差分后进行模型的假设,根绝ADF检验结果表明,差分后的对数收益率序列,见图2满足平稳时间序列的假设。
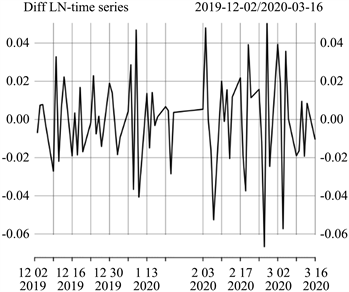
Figure 2. Rate of return difference series
图2. 收益率差分序列
描述性统计
在对使用差分后对数收益率进行建模分析之前,本文对对数收益率序列进行了整体的描述统计,结果见表1。
根据描述性统计,JB检验的P-value = 0.6392,我们有理由不拒绝服从正态分布的原假设,所以差分后的对数收益率近似的满足正态假定下的数据结构,对于之后的建模分析,在建模时,可以选择使用正态分布来对差分后的对数收益率序列进行预测分析。

Table 1. Descriptive statistical analysis table
表1. 描述性统计分析表
3.2. 建模分析
建立GARCH模型之前,首先要对序列进行ARCH效应的检验,若序列本身并不存在ARCH效应,则没有建立GARCH模型的必要。为了符号上的方便,记为均值方程的残差,则可以用平方序列来检验条件异方差性,即所谓的ARCH效应。Ljung-Box检验的P值为0.02053,小于0.05的显著性水平,所以我们有理由拒绝不存在ARCH效应的原假设,所以存在ARCH效应,可以进行GARCH建模分析。对平方序列做偏自相关图(见图3)进行ARCH模型的定阶。根据偏自相关图,选用低阶的GARCH模型,如GARCH(1, 1)模型、GARCH(1, 2)模型、GARCH(2, 1)模型等,便可以进行预测估计。
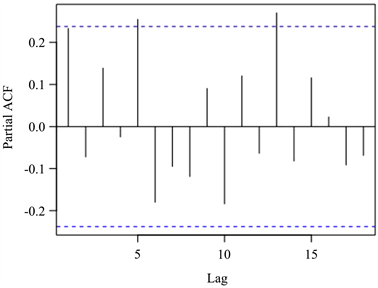
Figure 3. The partial autocorrelogram of
图3.
的偏自相关图
经过大量的回归检验及尝试对比,在对原始对数收益率序列建立EGARCH(1, 1)模型时,发现存在两个参数检验通不过的现象,而且根据赤池信息统计量最小的原则,最终对波动率的模型拟合选择了ARMA(1, 2)-GARCH(1, 1)模型,拟合后的GARCH模型为:
(17)
在模型的输出的回归结果中,各项系数都是十分显著的,并且给出了标准化残差的Ljung-Box白噪声检验结果,滞后10的p值为0.7244,承认白噪声;
的滞后10的Ljung-Box白噪声检验结果p值为0.5764在5%的显著性水平下也可以承认白噪声。所以ARMA(1, 2)-GARCH(1, 1)模型对波动率的拟合效果是比较好的。
3.3. 预测
在对模型进行选择之后,将2019年12月2日至2020年2月17日的数据做为实验数据进行模型估计,预测后12期的收益率变化,见图4。
在使用GRCH模型进行预测分析时,同样是选择以后12天的进行对比,从图中可以看出,GARCH模型与以后12天的估计有一个明显的上升趋势,并且会在第7天左右达到一个较平稳的状态,而实际情况在之后12天中存在明显的上下波动情况,并不是会在某一天趋于平稳的状态。见图5。

Figure 4. 12 steps ahead of the forecast
图4. 超前12步预测
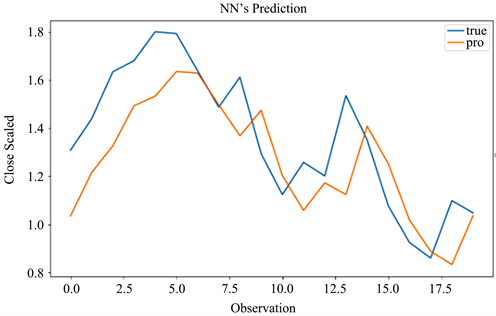
Figure 5. ANN model prediction results
图5. ANN模型预测结果
4. ANN模型的建立
在神经网络模型中将2019年12月2日至2020年2月15日的数据作为训练数据,2020年2月17日至2020年3月16日数据为检验数据,从而进行日收盘价的的预测。采用MinMaxScaler函数对数据进行归一化处理,将归一化的后的取值设定在[−1, 1],从而避免数据进入饱和区。创建一个序列模型,将医疗器械板块的日收盘价作为输入到第一层,输出维度为15,选用线性整流函数Relu (校正线性单位),损失函数选用平均绝对离差函数,为防止过拟合,选择早停法(Early Stopping),在5个周期内都没有出现提高则结束训练。最终训练结果用训练数据集、测试数据集的拟合优度来展示。利用上述假设,利用梯度下降法进行的ANN预测的结果如下。
ANN的训练数据得到的拟合优度为0.960,经过一系列参数的设定,最终测试数据得到的拟合优度为0.497。模型的训练数据集的误差达到很好的效果,在参数的选择方面,为避免过拟合现象,测试误差相比较而言偏大,但相比传统的GARCH模型,ANN模型的预测效果是优于GARCH模型的。序列的预测结果见图5。由图可知,ANN模型应用到医疗器械板块股票上的验证中,模型对于序列的波动性质拟合效果存在一定的滞后效果,本文的时间跨度区间仅仅选择了冠状病毒爆发的近100天,样本的大小也限制了模型的估计结果,但总体与传统的GARCH模型相比,充分考虑了序列的各个方面的特性,有效的抓住了非线性相关关系。为检验ANN模型的鲁棒性,选择了同时段的汽车板块的股票日收盘价作为输入。模型的预测结果见图2。由图2可知,ANN模型对选取的汽车板块股票测试中表现的依然良好,说明模型具有一定的鲁棒性。
5. 结论
针对股票市场中的非线性特征,选用ANN的模型算法与传统的GARCH模型对股票价格进行预测,结果表明选用ANN算法估计优于传统的GARCH模型估计,尽管使用最简单的ANN算法,并且由于数据的跨度较小,会产生一定的过拟合现象,但与传统的GARCH模型相对比,还是展现出了极强的预测能力。尤其是在趋势的预测上,使用ANN算法能够展现出股票日后趋势的大体走势。而传统的GARCH模型,对于时间跨度较短、波动较大的序列,没有展现出很好的估计效果,估计误差较大,在预估趋势方面也存在一定的差异。
致谢
感谢老师对课题研究与论文撰写的指导,对于该研究的实证模拟比较困难,在这一过程中,老师和同学都帮助了我很多,通过一步一步地悉心指导,帮助我完成了论文的撰写。此外,也感谢论文评阅老师们的辛苦工作。