基于分数阶反应扩散方程的传染病模型研究

Research on Epidemic Model Based on Fractional Reaction Diffusion Equation

摘要: 反应扩散方程在物理学、化学、医学及生物学等多个领域的不同模型中有广泛应用。分数阶反应扩散型方程是整数阶的推广，被广泛应用于研究传染病的传播过程、图像分析以及随机过程。本文采用分数阶反应扩散方程来模拟传染病模型的动态行为。首先，通过求解齐次Neumann边界条件下分数阶反应扩散方程的特征值，对其进行线性稳定性分析，得到图灵不稳定的条件。然后结合Kronecker积用有限差分法以及积分因子法在空间上以及时间上对反应扩散方程组进行离散并求解。最后，给出数值实验验证稳定性分析结果。本文的数值结果有助于预测传染病的流行趋势。

Abstract: Reaction diffusion equation is widely used in different models of physics, chemistry, medicine and biology. Fractional reaction diffusion equation is a generalization of integer order, which is widely used in the study of infectious disease propagation process, image analysis and stochastic process. In this paper, the fractional reaction-diffusion equation is used to simulate the dynamic behavior of the epidemic model. Firstly, by solving the eigenvalues of the fractional reaction-diffusion equation with homogeneous Neumann boundary conditions, the linear stability of the equation is analyzed, and the Turing instability condition is obtained. Then, combined with Kronecker product, the reac-tion-diffusion equations are discretized and solved by finite difference method and integration factor method in space and time. Finally, numerical experiments are given to verify the stability analysis results. The numerical results are helpful to predict the epidemic trend of infectious diseases.

1. 引言

传染病自古以来就是危害人类健康的主要敌人之一，此次暴发的新冠肺炎疫情在全球范围内都产生了巨大影响。面对日益严峻的传染病防控形势，传染病动力学模型 [1] [2] [3] 可以分析疾病的发展过程、产生的原因，有助于预测传染病流行趋势，进而为疾病的防控提供重要理论依据。目前，反应扩散模型是研究传染病的一种新模型，被广泛应用于研究传染病的斑图动力学以及疫情传播过程 [4] [5] [6]。反应扩散系统中，稳定态会在某些条件下失稳形成图灵斑图 [7]。通过求解反应扩散方程，可以得到图灵斑图以及固定模式之间的模式转换 [8]。在齐次Neumann边界条件下的反应扩散方程可以模拟流行病传播模型，研究其时空动力学可以发现病毒扩散范围对疾病形成的影响 [9]。本文研究分数阶反应扩散传染病模型的空间动力学模型，与经典的整数阶方程相比，分数阶算子的非局域性质能够捕捉空间异质性。但对于大多数分数阶微分方程，没有普遍有效的方法可以求得精确解。因此，采用数值方法模拟求解分数阶微分方程尤为重要。

近年来，许多学者利用有限元方法 [10]、有限差分方法 [11]、谱方法 [12]、间断Galerkin方法 [13] 等对反应扩散方程进行了研究。但是目前，对分数阶反应扩散传染病模型的研究很少 [14]。本文考虑具有齐次Neumann边界条件的分数阶反应扩散方程，利用分数阶拉普拉斯算子代替整数阶拉普拉斯算子。结合Kronecker积在空间上和时间上分别采用有限差分法和积分因子方法对反应扩散方程组进行离散。该方法不仅可以提高稳定性及计算效率，并且存储量小。最后，给出数值实验并对数值结果进行总结，验证了分数阶的取值对图灵斑图的产生有一定的影响。

2. 数值模型及线性稳定性分析

2.1. 分数阶传染病模型

假设空间环境连续地变化，个体随机迁移并以相同的机率向各个方向扩散，则可以用以下分数阶反应扩散方程来描述基于空间的传染病模型：

$\{\begin{array}{l}\frac{\partial S}{\partial t}=-D_1{\left(-\Delta \right)}^{\frac{{\alpha }_1}{2}}S+A-dS-\beta S^p{I}^q,\\ \frac{\partial I}{\partial t}=-D_2{\left(-\Delta \right)}^{\frac{{\alpha }_2}{2}}I+\beta S^p{I}^q-\left(d+\epsilon \right)I.\end{array}$ (1)

其边界条件为齐次Neumann边界，即 ${\frac{\partial S}{\partial n}|}_{\left(x,y\right)}=0,{\frac{\partial I}{\partial n}|}_{\left(x,y\right)}=0,\left(x,y,t\right)\in \partial \Omega \times \left(0,T\right]$。

其中 $\Delta =\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ 为二元整数阶拉普拉斯算子， $D_1,D_2$ 分别为易感个体和感染个体的扩散系数， $t$ 为时间变量，分数阶 ${\alpha }_1,{\alpha }_2\left(1<{\alpha }_1,{\alpha }_2\le 2\right)$ 分别取不同的值。 $S$ 表示易感健康人口， $I$ 表示能够将疾病传播给易感健康人口 $S$ 的感染人口， $A$ 表示人口的自然增长率， $d$ 表示人口的自然死亡率， $\epsilon$ 表示受感染者的疾病相关死亡率， $\Omega =\left[a,b\right]\times \left[c,d\right]$ 表示一个矩形区域， $\partial \Omega$ 表示边界的外导数。

2.2. 线性稳定性分析

下面考虑分数阶微分方程的其次稳态解及其稳定性。首先考虑二维空间 $\Omega$ 中具有齐次Neumann边界条件的特征值问题：

$\{\begin{array}{l}-\Delta u=\mu u,\\ {\frac{\partial u}{\partial n}|}_{\partial \Omega }=0.\end{array}$ (2)

上述问题的特征值和相应的特征函数分别为

${\mu }_{j,k}={\left(\frac{j\pi }{L_x}\right)}^2+{\left(\frac{k\pi }{L_y}\right)}^2.$ (3)

${\varphi }_{j,k}=\sqrt{\frac{2}{L_x}}\sqrt{\frac{2}{L_y}}\cos \frac{j\pi \left(x-a\right)}{L_x}\cos \frac{k\pi \left(y-c\right)}{L_y},\left(j\in Z,k\in Z\right).$ (4)

其中 $L_x=b-a,L_y=d-c$。省略系统中的分数阶扩散项，则(1)式化为

$\{\begin{array}{l}\frac{dS}{dt}=A-dS-\beta S^p{I}^q,\\ \frac{dI}{dt}=\beta S^p{I}^q-\left(d+\epsilon \right)I.\end{array}$ (5)

设对应于 $A-dS-\beta S^p{I}^q=0$， $\beta S^p{I}^q-\left(d+\epsilon \right)I=0$ 的齐次稳态解为 $\left(s^{*},i^{*}\right)$，通过 $\left(\tilde{S},\tilde{I}\right)=\left(S-s^{\ast },I-i^{\ast }\right)$ 将 $\left(s^{*},i^{*}\right)$ 平移到原点，并将 $\tilde{S},\tilde{I}$ 分别表示为 $S,I$。下面对非线性常微分方程(5)在稳态解附近进行线性化得到：

$\frac{d}{dt}\left(\begin{array}{c}S\\ I\end{array}\right)=\left(\begin{array}{cc}{f}_S& f_I\\ g_S& g_I\end{array}\right)\left(\begin{array}{c}S\\ I\end{array}\right).$ (6)

当雅可比矩阵 $J=\left(\begin{array}{cc}{f}_S& f_I\\ g_S& g_I\end{array}\right)=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)$ 特征值的实部为负时，即 $\mathrm{Re}\left(\lambda \right)<0$，齐次稳态解 $\left(S,I\right)=\left(0,0\right)$ 是稳定的。下面加上分数阶扩散项，将方程组(1)式线性化得到：

$\{\begin{array}{l}\frac{\partial S}{\partial t}=-D_1{\left(-\Delta \right)}^{\frac{{\alpha }_1}{2}}S+a_{11}S+a_{12}I,\\ \frac{\partial I}{\partial t}=-D_2{\left(-\Delta \right)}^{\frac{{\alpha }_2}{2}}I+a_{21}S+a_{22}I.\end{array}$ (7)

为了研究分数阶反应扩散系统(1)的扩散驱动不稳定性条件，需要在本文边界条件下计算下列方程的特征值：

$\{\begin{array}{l}\lambda S=-D_1{\left(-\Delta \right)}^{\frac{{\alpha }_1}{2}}S+a_{11}S+a_{12}I,\\ \lambda I=-D_2{\left(-\Delta \right)}^{\frac{{\alpha }_2}{2}}I+a_{21}S+a_{22}I.\end{array}$ (8)

设 $S,I$ 被一组完整的正态分布特征函数 $S={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\hat{S}}_j{\varphi }_j}$ 和 $I={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\hat{I}}_j{\varphi }_j}$ 分解，并将其代入(8)式，得到下列线性代数系统：

$\begin{array}{l}\left(-D_1{\mu }^{\frac{{\alpha }_1}{2}}+a_{11}-\lambda \right){\hat{S}}_j+a_{12}{\hat{I}}_j=0,\\ a_{21}{\hat{S}}_j+\left(-D_2{\mu }^{\frac{{\alpha }_2}{2}}+a_{22}-\lambda \right){\hat{I}}_j=0.\end{array}$ (9)

其中 $\mu ={\left(\frac{j\pi }{L_x}\right)}^2+{\left(\frac{k\pi }{L_y}\right)}^2$。当 $\left|\begin{array}{cc}-D_1{\mu }^{\frac{{\alpha }_1}{2}}+a_{11}-\lambda & a_{12}\\ a_{21}& -D_2{\mu }^{\frac{{\alpha }_2}{2}}+a_{22}-\lambda \end{array}\right|=0$ 时，齐次线性方程组(9)有非零解，其对应的特征多项式为

${\lambda }^2-\left(a_{11}+a_{22}-D_1{\mu }^{\frac{{\alpha }_1}{2}}-D_2{\mu }^{\frac{{\alpha }_2}{2}}\right)\lambda +\left(a_{11}-D_1{\mu }^{\frac{{\alpha }_1}{2}}\right)\left(a_{22}-D_2{\mu }^{\frac{{\alpha }_2}{2}}\right)-a_{12}{a}_{21}=0.$ (10)

解得其特征值为

$\begin{array}{c}\lambda =\frac{1}{2}\{\left(a_{11}+a_{12}-D_1{\mu }^{\frac{{\alpha }_1}{2}}-D_2{\mu }^{\frac{{\alpha }_2}{2}}\right)\pm {[\left(a_{11}+a_{12}-D_1{\mu }^{\frac{{\alpha }_1}{2}}-D_2{\mu }^{\frac{{\alpha }_2}{2}}\right)}^2\\ -4{\left(\left(a_{11}-D_1{\mu }^{\frac{{\alpha }_1}{2}}\right)\left(a_{22}-D_2{\mu }^{\frac{{\alpha }_2}{2}}\right)-a_{12}{a}_{21}\right)]}^{\frac{1}{2}}\}.\end{array}$ (11)

若 $\max \lambda \left(\mu \right)>0$，则系统将变得不稳定，进而形成图灵斑图。函数 $\lambda \left(\mu \right)$ 被称为色散曲线，从中可以得到关于非均匀平稳模态存在的信息。

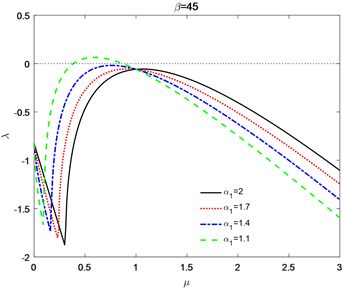
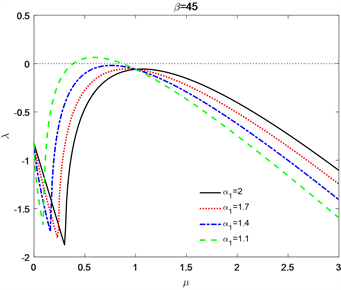
(a) ${\alpha }_1=1.1,1.4,1.7,2,{\alpha }_2=2$ (b) ${\alpha }_1=2,{\alpha }_2=1.1,1.4,1.7,2$

Figure 1. Dispersion curves of various conditions by only changing one of the parameters of ${\alpha }_1,{\alpha }_2$

图1. 仅改变 ${\alpha }_1,{\alpha }_2$ 其中一个参数时的不同情况下的色散曲线

在以往对分数阶流行病模型 [14] 的研究中，参数值设为 $A=1,\epsilon =1.8,d=1,D_1=6,D_2=1,\beta =45$。当改变分数阶拉普拉斯算子的阶数 ${\alpha }_1$ 或 ${\alpha }_2$ 时，不同情况对应的色散曲线如图1所示。可以看出，系统(1)在整数阶 ${\alpha }_1={\alpha }_2=2$ 的情况下是稳定的，将不会生成图灵斑图。随着 ${\alpha }_1$ 递减， $\max \lambda \left(\mu \right)$ 由负变为正，这意味着随着时间的变化，系统(1)将变得不稳定。图1(b)显示的是当固定 ${\alpha }_1=2$ 时， ${\alpha }_2$ 取值不同情况下对应的色散曲线。在 ${\alpha }_1=2$ 和 ${\alpha }_2=2,1.7$， $\lambda \left(\mu \right)<0$ 的情况下，系统是稳定的。而在其他情况下，即 ${\alpha }_2=1.4,1.1$ 时，由于 $\lambda \left(\mu \right)$ 有正值和负值，系统会振荡。因此在这种情况下，可以观察到各种图灵斑图。该数值结果表明，分数阶拉普拉斯算子的阶数可以影响和控制系统的稳定性。

3. 数值方法

本文以(1)式中的第一个方程为例进行求解，第二个方程的求解形式类似。在空间离散过程中，采用有限差分方法求解分数阶反应扩散方程(1)。将计算区域 $\Omega$ 等距剖分为 $M\times N$ 个网格，网格节点为 $\left(x_j,y_k\right)$，其中 $x_j=a+\left(j-1/2\right)h_x$， $y_k=c+\left(k-1/2\right)h_y$， $j=1,\cdots ,M$， $k=1,\cdots ,N$，网格步长分别为 $h_x=L_x/M$， $h_y=L_y/N$。设 $s$ 在网格节点 $\left(x_j,y_k\right)$ 的数值解为 $s_{j,k}$，定义离散解 $s_{j,k}$， $1\le j\le M$， $1\le k\le N$ 为 $M\times N$ 阶的矩阵 $S$。由本文边界条件，在网格内部点 $\left(x_j,y_k\right)$ 和边界处的二阶导数差分格式分别为

${\frac{{\partial }^{2}s}{\partial x^2}|}_{j,k}=\frac{1}{h_x{}^2}\left(s_{j-1,k}-2s_{j,k}+s_{j+1,k}\right)+O\left(h^2\right).$ (12)

${\frac{{\partial }^{2}s}{\partial x^2}|}_{\text{1},k}=\frac{1}{h_x{}^2}\left(-s_{1,k}+s_{2,k}\right)+O\left(h^2\right).$ (13)

由差分格式(12)和(13)式，得到该方程在 $x,y$ 方向的微分矩阵分别为 $B_x$ 和 $B_y$ ：

$B_x={\left(\begin{array}{cccccc}1& -1& 0& 0& \cdots & 0\\ -1& 2& -1& 0& \cdots & 0\\ 0& -1& 2& -1& \cdots & 0\\ ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& 0& 0& -1& 2& -1\\ 0& 0& 0& 0& -1& 1\end{array}\right)}_{M\times M},B_y={\left(\begin{array}{cccccc}1& -1& 0& 0& \cdots & 0\\ -1& 2& -1& 0& \cdots & 0\\ 0& -1& 2& -1& \cdots & 0\\ ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& 0& 0& -1& 2& -1\\ 0& 0& 0& 0& -1& 1\end{array}\right)}_{N\times N}$

设 $E_x,E_y$ 分别为 $M,N$ 阶单位矩阵，首先将解矩阵 $S$ 表示为如下形式：

$\mathcal{S}=\text{vec}\left(S\right)={\left(s_{1,1}\cdots s_{M,1},s_{1,2}\cdots s_{M,2},\cdots ,s_{1,N}\cdots s_{M,N}\right)}^{\text{T}}.$ (14)

结合(12)~(13)式以及Kronecker积，可以将(1)式的二阶中心差分格式写成如下形式：

$\frac{\text{d}\mathcal{S}}{\text{d}t}=-D_1{\left(E_y\otimes \frac{1}{h_x{}^2}{B}_x+\frac{1}{h_y{}^2}{B}_y\otimes E_x\right)}^{\frac{{\alpha }_1}{2}}\mathcal{S}+f\left(\mathcal{S},\mathcal{I}\right).$ (15)

将矩阵 $B_x$ 正交化，得到：

$B_x=C_x{}^{\text{T}}\Lambda C_x=C_x{}^{-1}\Lambda C_x,$ (16)

进而(15)式可以写为

$\frac{\text{d}S}{\text{d}t}=\mathcal{A}\mathcal{S}+F\left(\mathcal{S},\mathcal{I}\right),$ (17)

其中 $\mathcal{A}=-D_1{\left(C_y\otimes C_x\right)}^{-1}{\left(I_y\otimes \frac{1}{\Delta x^2}{\Lambda }_x+\frac{1}{\Delta y^2}{\Lambda }_y\otimes I_x\right)}^{\frac{{\alpha }_1}{2}}\left(C_y\otimes C_x\right)$。

下面应用积分因子法对(17)式进行求解，将(17)式两端同时左乘 ${\text{e}}^{-\mathcal{A}t}$，并从 $t_n$ 到 $t_{n+1}=t_n+\Delta t$ 进行积分得到：

${\mathcal{S}}_{{}^{n+1}}={\text{e}}^{\mathcal{A}\Delta t}\left({\mathcal{S}}_{{}^n}+\frac{\Delta t}{2}F\left({\mathcal{S}}_{{}^n},{\mathcal{I}}_{{}^n}\right)\right)+\frac{\Delta t}{2}F\left({\mathcal{S}}_{{}^{n+1}},{\mathcal{I}}_{{}^{n+1}}\right).$ (18)

令 $W_n=S_n+\frac{\Delta t}{2}F\left(S_n,I_n\right)$，对 $W_n$ 向量化，即 ${\mathcal{W}}_n=\text{vec}\left(W_n\right)={\mathcal{S}}_{{}^n}+\frac{\Delta t}{2}F\left({\mathcal{S}}_{{}^n},{\mathcal{I}}_{{}^n}\right)$。

由于矩阵 $A$ 可以对角化，有 ${\text{e}}^{A\Delta t}={\left(C_y\otimes C_x\right)}^{-1}{\text{e}}^{-D_1{\left(I_y\otimes \frac{1}{\Delta x^2}{\Lambda }_x+\frac{1}{\Delta y^2}{\Lambda }_y\otimes I_x\right)}^{\frac{{\alpha }_1}{2}}}\left(C_y\otimes C_x\right)$。可结合Kronecker积对 ${\text{e}}^{\mathcal{A}\Delta t}{\mathcal{W}}_n$ 进行求解，并将其向量化，将(18)式表示为如下形式：

${\mathcal{U}}_{{}_{{}^{n+1}}}^{}={\mathcal{H}}_3+\frac{\Delta t}{2}F\left({\mathcal{S}}_{{}^{n+1}}^{{}^{}},{\mathcal{I}}_{{}^{n+1}}^{{}^{}}\right).$ (19)

采用不动点迭代法求解，其迭代初值选取为 ${\mathcal{S}}_{n+1}^0={\mathcal{S}}_n^{}$。

4. 数值实验

应用本文提出的数值方法，下面将给出数值模拟来验证线性稳定性的分析结果，并对数值模拟结果进行分析。在区域 $\Omega ={\left[-50,50\right]}^2$ 上求解分数阶传染病模型(1)式。取参数 $A=1,\epsilon =1.8,d=1,$ $D_1=6,D_2=1$和 $\beta =45$。由于图1中表明，对于整数阶的情况，即 ${\alpha }_1={\alpha }_2=2$，没有图灵斑图。因此，为了得到图灵斑图，下面对均匀分布进行随机扰动：

$S\left(x,y,0\right)=s^{*}+\delta \ast rand\left(x,y\right),I\left(x,y,0\right)=i^{*}+\delta \ast rand\left(x,y\right)$

其中 $\delta ={10}^{-3}$， $rand\left(x,y\right)$ 表示取 $-1$ 和1之间的随机数。本文在 $100\times 100$ 个空间单元的系统中进行了数值模拟。将时间步长取为 $\tau =0.01$，并进行仿真，直到它们达到静止状态。未感染者 $S$ 的分布图像经过100次、1000次、10,000次、50,000次迭代保存。

下面将固定其中一个分数阶阶数，改变另一个分数阶阶数，进行一系列的数值模拟。首先固定 ${\alpha }_2=2$，取 ${\alpha }_1=1.1$。由图1的色散曲线可以看出，特征值的最大值为正。因此，图灵斑图会随着时间的变化而出现。

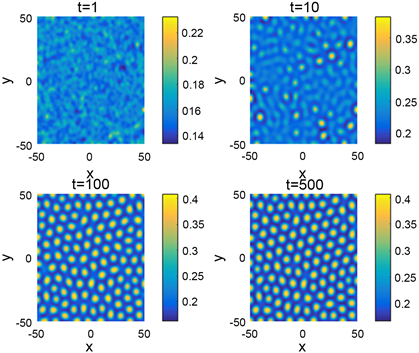
Figure 2. Turing patterns for ${\alpha }_1=1.1$ and ${\alpha }_2=2$

图2. ${\alpha }_1=1.1$ 和 ${\alpha }_2=2$ 的图灵斑图

由图2可以看出，初始随机扰动最终导致了光斑的形成。蓝色背景上的黄色六边形表示未被感染的人群是高度人口密度的隔离区域。然后取 ${\alpha }_1=1.4$，由图3可以观察到已经达到平衡态，没有图灵斑图出现。

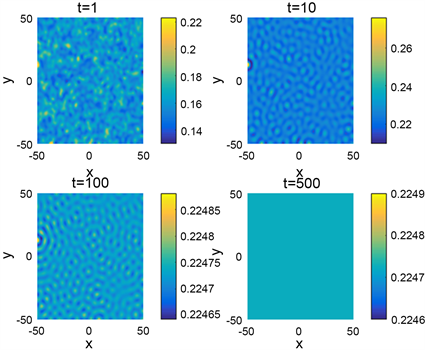
Figure 3. Turing patterns for ${\alpha }_1=1.4$ and ${\alpha }_2=2$

图3. ${\alpha }_1=1.4$ 和 ${\alpha }_2=2$ 的图灵斑图

接下来，固定 ${\alpha }_1=2$，取 ${\alpha }_2=1.1$。由图4可以看出，在这种情况下，随着时间的推移，流行病模型表现出从条纹–空洞模式向空洞模式的转变。黄色背景上的蓝洞表示未感染者为低人口密度隔离区。固定 ${\alpha }_1=2$，取 ${\alpha }_2=1.4$。由图5可以看出，一开始只有模糊的斑点模式。经过一段时间的整合后，形成条纹状的图案，并随着时间的推移逐渐增长，直到达到一定的臂长。最后得到了感染种群密度分布中固定条纹和斑点的混合模式。综上所述，分数阶拉普拉斯算子的阶数的选择对图灵斑图的生成具有一定影响。

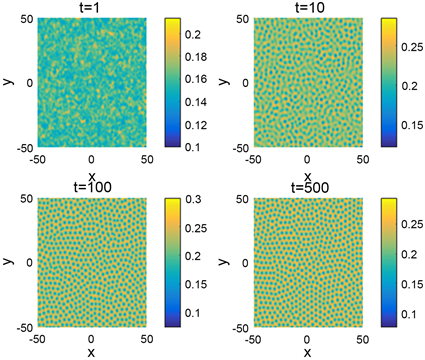
Figure 4. Turing patterns for ${\alpha }_1=2$ and ${\alpha }_2=1.1$

图4. ${\alpha }_1=2$ 和 ${\alpha }_2=1.1$ 的图灵斑图

Figure 5. Turing patterns for ${\alpha }_1=2$ and ${\alpha }_2=1.4$

图5. ${\alpha }_1=2$ 和 ${\alpha }_2=1.4$ 的图灵斑图

5. 总结

本文提出了分数阶反应扩散方程流行病模型，并分析本文边界条件下的线性稳定性，得到分数阶拉普拉斯算子的阶数可以影响和控制系统的稳定性。此外，采用有限差分方法与积分因子方法分别对分数阶反应扩散方程进行空间与时间离散，提高了计算效率。最后进行数值模拟，得到流行病系统不稳定时的图灵斑图，确定了图灵斑图产生的部分影响因素。本文的方法和结果对反应扩散方程流行病模型的研究有一定贡献，可以预测某些流行病的空间传播以及扩散趋势，在今后可以更好地预防和控制传染病的传播。