林达滑坡内部1#次级滑体稳定性研究

Study on Stability of 1# Secondary Sliding Body in the Interior of Linda Landslide

摘要: 林达滑坡的稳定性问题对其上游林达电站、下游乐安电站、乐安乡及尼古寺的安全至关重要。本文利用GeoStudio软件根据滑坡体地质模型，构建典型剖面的渗流分析模型，采用有限元GeoStudio渗流分析模块SEEP模拟渗流。运用SLOPE模块对林达滑坡进行稳定性刚体极限平衡分析。分析研究表名：天然工况下，林达滑坡主滑体内1#次级滑体处于稳定状态；暴雨工况下，主滑体内1#次级滑体处于基本稳定–稳定状态。本文的研究为今后林达滑坡的稳定性安全设计和评价提供了一定的参考依据。

Abstract: The stability of the Linda landslide is of great importance to the safety of the upstream Linda power station, the downstream Le’an power station, Le’an township and Nigu temple. In this paper, GeoStudio software is used to build the seepage analysis model of typical section according to the geological model of landslide body, and the finite element GeoStudio seepage analysis module SEEP is used to simulate seepage. The SLOPE module is used to analyze the rigid limit equilibrium of the Linda landslide stability. Table name of analysis and research: under natural working condition, No. 1 secondary sliding body in main sliding body of Linda landslide is in stable state; under the rainstorm condition, the #1 secondary sliding body in the main sliding body is in the basic stable-stable state. The research in this paper has provided a certain reference basis for the sta-bility and safety design and evaluation of Linda landslide in the future.

1. 引言

中国的滑坡灾害十分频繁，我国土地总面积的65%以上是山地地形，到目前为止大约将近20%~25%的山地地形存在滑坡的威胁。近15年来，发生了许多摧毁性很严重的大型崩滑事件 [1] [2] [3] [4] [5]。历年来发生的许多大型滑坡所造成的损害是难以估量的，如：因为受到地震能量的影响，在08年汶川地震过后出现了大量的滑坡案例。2010年的重庆武隆“6·5”特大滑坡灾害，以及发生在西藏昌都的较大规模山体滑坡。可见我国的滑坡灾害遍布全国各地而且破坏性比较大，已经严重影响到人们的生存与生活的方方面面，因此，对滑坡的综合治理来说关于滑坡的灾害提前预报显得更加重要。为此，本文针对我国滑坡的现状，对林达滑坡是否可能发生崩滑进行了系统的分析研究，来提高预测的准确性与可靠性，减少滑坡灾害所造成的各种损失，来保障人民的人生安全与财产安全以及我国地形地貌的完整性。

2. 研究现状与内容

初始阶段，对于滑坡治理的早就开始于上世纪二十年代欧洲的瑞典，并且由瑞典的学者彼得森首先提出后来被命名为瑞典条分法的研究方法。但在接下来的20年左右的时间里，世界各地对山体滑坡的研究都是基于瑞典条分法的研究，显得十分的局限与片面。由于瑞典条分法成立的基础是将研究对象视为刚体，并且在刚体的极限平衡的条件下成立。其相对比较出名的代表的研究方法还有瑞典条分 [6]、简化毕肖普 [7]、传递系数法 [8]、简布法 [9]、斯宾塞法 [10]、Morgenstern-Price法 [11] 等。

初始发展阶段(20世纪50年代)，滑坡体内部的相对结构面与构成滑坡体的土体与岩石的开始成为新的研究对象，随着理论研究的深入，出现了极限平衡理论和弹塑性理论，同时在边坡问题的具体实际上，对于极限平衡法的应用开始变得越来越成熟，不仅如此随着时间的发现也对此方法在不同问题的应用做了合适的完善 [12] [13] [14] [15]。因为影响滑坡的因素具有不确定性与随机性，从而对于滑坡的相对的评价方法也变得各不相同，存在不同角度与方式的方法，其中比较具有代表性的方法有神经网络法、模糊数学法和灰色理论法等等一系列相关的方法 [16] [17]。

深入发展阶段(20世纪60年代)，这个阶段的改变就是利用极限平衡法为基础，去研究分析滑坡体内部关于结构面之间的稳定性分析。同时利用全新的计算机分析方法来计算滑坡体的安全稳定性系数，并且由此来确定滑坡体的相对稳定性。此外，John也提出了图解法。

具体研究内容包括以下四点：1) 工程地质环境条件的研究；2) 林达滑坡基本特征研究：滑坡边界条件、物质组成、滑坡工程地质分区、变形分带特征、变形破坏现象、影响因素、成因与机理等，进一步抽象出滑坡相关基本概念的地质力学相关模型，并且依据相关的数据来对滑坡坡段的局部以及整体的稳定性进行判定。3) 接着通过一系列的物理实验来得出边坡体的相关物理力学参数，并联系实际的工程类比更进一步的来探究确定话滑坡带相关岩土体物理参数取值；4) 此次研究选取林达滑坡体内部1#次级滑坡的典型坡面，并且选用传统的极限平衡法来调查不同情况下的稳定性分析。

3. 研究区概况

雅砻江上游乐安梯级水电站库区位于四川省甘孜藏族自治州境内，隶属于甘孜藏族自治州新龙县行政区。在县城及其周围的乐安乡、角多、大盖乡、次措等地人口分布密集。库区内交通较为便利，整个库区沿江有省道S217通过，大部分河段有通县乡道路，部分河段沿江有国道及省道相通(图1)。

Figure 1. A sketch map of traffic location and administrative divisions

图1. 交通位置及行政区划简图

乐安水库河段地处于青藏高原东南部，毗邻川西南高区，其地势为呈现为北向南倾斜，地貌区属于川西高原。地貌基本形态是具夷平面的大起伏高山，山势海拔高程多在3000 m之上。河谷两岸为高达数百米至千米以上的陡峻岸坡，库区属典型的高山峡谷型地貌(如图2)。河谷呈现为“V”型峡谷，谷坡坡度一般都超过40˚。

4. 滑坡基本特征及岩体力学参数

林达滑坡在乐安水电站库区右岸，距离下坝址上游大概5.5~6.7 km。雅砻江流向近SN向，滑坡所在的江水水位约为3142 m，江面宽度约为54 m，滑坡堆积体总面积约为6 × 10⁵ m²。勘探结果表示，滑坡体分布总体呈前缘薄，中后部厚的形态，前缘平均厚度约为15 m，中后部相对较厚，平均厚度约为75 m，估计总体积为3390 × 10⁴ m³。滑坡堆积体后缘高程约为3770 m，前缘直抵河床，高程约为3141 m，相对高差约为630 m (如图3、图4)。

滑坡在平面上呈锥形，两侧以冲沟为界，后缘发育有明显的下错台坎，此外还出露有约10 m高的基岩陡壁，前缘直抵河床。堆积体整体坡度较陡，且前缘比坡体后部要陡。根据地表调查及地质勘探成果，林达滑坡目前内部有四处局部次级滑体，从下游至上游，依次为：1#次级滑体、2#次级滑体和3#次级滑体，主滑动体位于滑坡体的中后部。

Figure 2. Typical alpine and valley landforms in the reservoir area

图2. 库区典型高山峡谷型地貌

Figure 3. Linda landslide engineering geological plan

图3. 林达滑坡工程地质平面图

Figure 4. Section II-II of Linda landslide

图4. 林达滑坡II-II剖面图

滑坡渗流模拟、变形破坏及稳定性分析中，选择合理的岩土物理力学参数非常重要。目前确定滑带土抗剪强度参数(C、Φ)有工程类比、实验法和反演分析三种。此案例根据物理力学性质试验成果，结合工程类比，深入研究滑坡体各分带岩土体的参数取值。计算参数主要为滑体重度、滑带土的抗剪强度等，结合类比分析确定其值。分析计算参数取值汇总，见表1。

Table 1. Seepage analysis of Linda landslide and summary table of numerical model parameter values

表1. 林达滑坡渗流分析、数值模型参数取值汇总表

5. 基于GeoStudio的软件模拟

5.1. 渗流场数值模拟的理论原理

SEEP/W模块以达西定律为基本原理，法国水利学家达西(H. Darcy)于1856年研究水通过均匀砂柱孔隙的渗流实验，提出了线性渗透定律，就是著名的达西定律 [18]。其可用公式表述为：

Q是单位体积流量，ΔH为水头差，ΔH/ΔL为水力梯度，K_s为饱和渗透系数。

采用有限元GeoStudio渗流分析模块SEEP来计算林达滑坡在库水位波动以及降雨作用下，其变形发展过程及其稳定性。采用饱和–非饱和渗流理论计算林达滑坡地下水渗流场的动态变化过程。二维饱和–非饱和渗流微分方程可由Darcy定律和质量守恒定律联合推导得出，当采用水头h作为控制方程的因变量时，渗流微分方程可以写成如下形式：

$\frac{\partial }{{\partial }_x}\left[K_x\frac{{\partial }_h}{{\partial }_x}\right]+\frac{\partial }{{\partial }_y}\left[K_y\frac{{\partial }_h}{{\partial }_y}\right]+Q=m_w{r}_w\frac{{\partial }_h}{{\partial }_t}$

K_x，K_y分别为水平和垂直方向的饱和渗透系数；h为总水头；Q为施加的边界流量；m_w为比水容积；r_w为水的重度。

5.2. 滑坡稳定性计算的理论原理

SLOPE/W模块以极限平衡法为原理，主要针对岩土体边坡稳定性、边坡开挖、地震荷载等问题进行分析。除此之外SLOPE/W还可以用来对边坡添加锚索、织物、土钉、抗滑桩用以提高边坡的稳定性。极限平衡理论方法在前文已经详细介绍这里不再赘述。

5.3. 地质模型的建立

根据以上研究结果，明确了主滑坡对整个滑坡起着控制作用。因此选取滑坡体的主滑剖面“II-II”建立数值计算模型(图5)。该滑坡地质模型可分为7层，主滑坡体、正常岩体、弱变形区、强变形区、滑坡体内部1#次级滑体、滑坡体内部2#次级滑体和2#次级滑体。由于该软件内置边界默认为不透水边界，并且林达滑坡的左、右两侧边界可以按照不透水边界来进行渗流计算，故将其II-II坡面设为基本滑动面。依据区域水文地质资料及勘探成果，设定滑坡后缘水位高程为3300 m，为定水头边界。对林达滑坡的稳定性计算按照正常水位和暴雨两种工况进行计算：

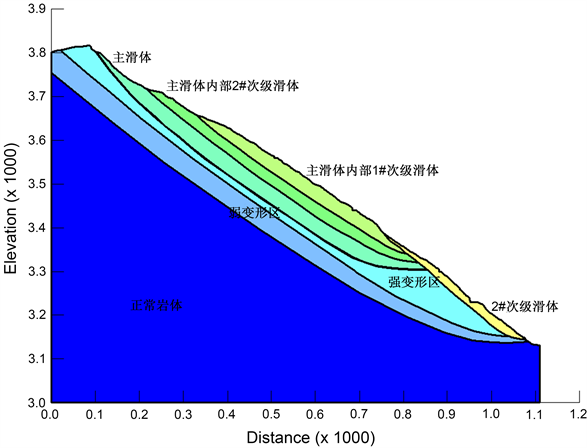
Figure 5. Sectional view of the section seepage model

图5. 剖面渗流模型剖面图

在进行渗流场计算时，左、右两侧边界设为不透水边界，坡面按照水位变化设为动水头边界。依据区域水文地质资料及勘探成果，设定滑坡后缘水位高程为3290 m，为定水头边界，不随库水位涨落而发生改变。通过上述模型，采用SEEP渗流分析模块，以1 d为时步间隔，计算获取林达滑坡在库水位升降过程中的动态地下水渗流场。考虑到主滑体内部次级滑体分两种情况，但由于主滑体不受蓄水水位的影响，故选取情况1的模型进行分析。

5.4. 模拟工况的选取

为研究林达滑坡在水库调度过程中的地下水动态渗流过程，以勘察期库水位3141 m为初始水位，从研究的目的出发，分别考虑以下2种工况条件进行分析计算：

工况一：天然状态滑体自重

工况二：天然状态滑体自重 + 暴雨

其中暴雨按50 mm/d的降雨强度考虑。

5.5. 计算结果及稳定性评价

渗流场结果与分析

根据图6~9，在降雨作用下，林达滑坡的地下水渗流场有较为明显的变化，且变化主要集中在滑体表层。当库水位从3145升至3148并伴随50 mm/d的强度降雨时，前缘次级滑体浸润线以内凹型并有一定程度的抬升，抬升速度大于无降雨条件。由此可见，降雨对林达滑坡的地下水渗流场有一定的影响，且主要集中在改为前缘次级滑体的前缘。在较大的动水、静水压力作用下，对前缘次级滑体的稳定性有一定影响。

Figure 6. Transient change of groundwater level in working condition I of section II-II

图6. II-II剖面工况一地下水位瞬态变化图

Figure 7. Contour map of pore water pressure in working condition I of section II-II

图7. II-II剖面工况一空隙水压力等值线图

Figure 8. Transient change of groundwater level in section II-II condition 2

图8. II-II剖面工况二地下水位瞬态变化图

Figure 9. Contour map of pore water pressure under section II-II condition 2

图9. II-II剖面工况二空隙水压力等值线图

5.6. 滑坡稳定性分析

目前最常用的Bishop法和Janbu法，均只考虑了条间法向力，而忽略了条间切向力，且Janbu法仅能满足水平向的法向力平衡，而不能满足力矩平衡 [19]；而Morgenstern-Price法(简称M-P法)不仅考虑了条间正应力，还考虑了条间剪应力，且同时满足力平衡与力矩平衡 [20]。本文将分别论述它们的计算结果并加以比较。

5.6.1. 计算原理及公式

根据勘察资料和前人研究的结论，综合确定林达滑坡的滑动面为折线型，所以选择传递系数法 [21] 对滑坡稳定性进行计算，稳定性系数K计算公式如下：

$K=\left\{{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}\left[R_i{\displaystyle \underset{j=i}{\overset{n-1}{\prod }}{\psi }_j}\right]}+R_n\right\}/\left\{{\displaystyle \underset{i=1}{\overset{n-1}{\sum }}\left[T_i{\displaystyle \underset{j=i}{\overset{n-1}{\prod }}{\psi }_j}\right]}+T_n\right\}$

其中： $R_n=\left[W_n\left(\left(1-r_u\right)\cos {\alpha }_n\right)-R_{Dn}\right]\tan {\psi }_n+C_n{L}_n$

$T_n=W_n\left(\sin {\alpha }_n+A\cos {\alpha }_n\right)-T_{Dn}$

式中：

${\psi }_j$ 是第i块段的剩余下滑力传递至第i + 1块段时的传递系数(j = i)，即

${\psi }_j=\cos \left({\alpha }_i-{\alpha }_{i+1}\right)-\sin \left({\alpha }_i-{\alpha }_{i+1}\right)\tan {\psi }_{i+1}$

r_u——孔隙压力比，可表示为：

$r_u\approx \frac{滑坡水下面积}{滑坡总面积\ast 2}$

5.6.2. 计算剖面的选取

为了对滑坡稳定性进一步分析求证，综合分析该滑坡自有特点，采用传递系数法对林达滑坡进行稳定性计算，选取滑坡变形区内包含1#次级滑体和主滑动体的II-II (详见图3，滑坡工程地质平面图)，建立其计算模型(如图10)采用局部搜索法和指定滑面法，计算1#次级滑体的稳定性。

Figure 10. II-II section calculation model

图10. II-II剖面计算模型

5.6.3. 计算工况的类别

考虑到滑坡体在实际土层中含有碎石、受到地下水、大气降水下渗等因素的影响故采用以下二种工况进行计算，并以暴雨状态下的稳定性计算结果为稳定性评价的首要考虑结果(如表2)。

Table 2. Summary of working conditions for landslide stability calculation

表2. 滑坡稳定性计算工况汇总表

5.6.4. 计算参数及计算条件

综合考虑野外钻探、地质分析及室内岩土测试结果，结合经验确定。根据滑面形态、含水性差异、滑面物质组成及滑面粗糙程度，取值略有差异。该滑坡计算参数具体取值如下表3。

Table 3. Landslide parameter table

表3. 滑坡参数表

5.6.5. 滑坡稳定性计算及综合评价

采用传递系数法对滑坡稳定性进行分析，利用上述确定的岩土体参数，选取了林达滑坡II-II剖面作为计算剖面，分别计算各剖面在天然工况、暴雨情况下的稳定系数，判断滑体所处的状态。本文根据《水电水利工程边坡工程地质勘察技术规程》(DL/T5337-2006)滑坡稳定状态划分标准，对滑坡各典型剖面的稳定性状况进行评价(如表4)。

Table 4. Landslide stability evaluation standard

表4. 滑坡稳定性评价标准

如图11，其他天然工况方法下的稳定性分析以此类推，这里不一一放图，具体结果见后表。

由表5可知，内部1#次级滑体在II-II剖面上稳定性系数均大于1.15，所以天然工况下内部1#次级滑体处于稳定状态。

如图12，其他暴雨工况方法下的稳定性分析以此类推，这里不一一放图，具体结果见后表。

由表6可知，内部1#次级滑体在II-II剖面上的稳定性系数分别为1.05、1.06、1.06、1.07，处于基本稳定–稳定状态。

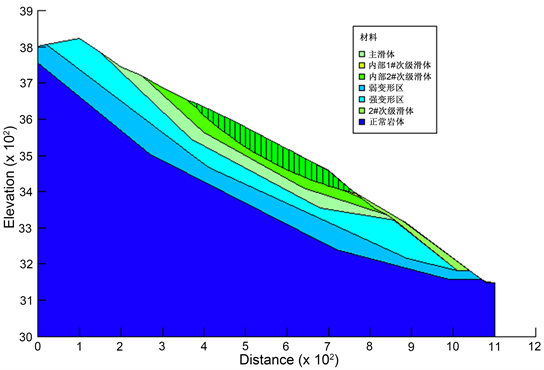
Figure 11. Morgenstern-Price method for stability analysis under natural conditions

图11. 天然工况下稳定性分析Morgenstern-Price方法

Table 5. Natural working condition 1# secondary sliding body stability calculation results

表5. 天然工况1#次级滑体稳定性计算结果

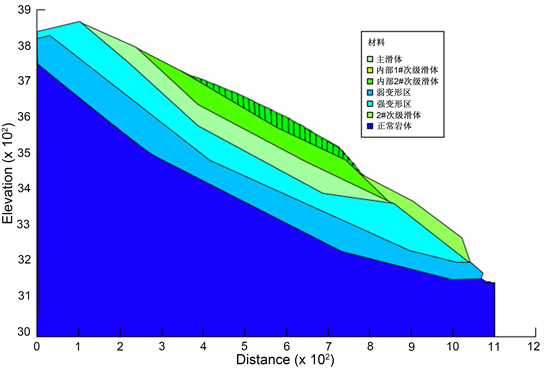
Figure 12. Morgenstern-Price method of stability analysis under heavy rain conditions

图12. 暴雨工况下稳定性分析Morgenstern-Price方法

Table 6. The calculation results of the stability of the secondary sliding body in the rainstorm condition 1#

表6. 暴雨工况1#次级滑体稳定性计算结果

6. 结论与建议

6.1. 结论

本论文通过对林达滑坡的背景资料分析，分析了林达滑坡的形成机制，并对滑坡稳定性进行了评价，在建立模型的基础上又深入研究了滑坡渗流场稳定性变化的过程。本文取得如下结论：

1) 根据野外地质勘探及调查综合分析，导致林达滑坡可能滑动的原因是水文因素、地质因素共同影响的。水文因素方面：林达滑坡水位线最高达到3154 m，降雨是滑坡滑动的主要水文因素也是重要诱发因素。此外，滑坡区地下水位埋深较浅也可能诱发滑坡发生。地质因素方面：乐安水电站水库区所处大地构造位置属特提斯–喜马拉雅造山系东缘的松潘–甘孜造山带核心部位，该地区地层受构造活动作用完整性较差，地形复杂。

2) 滑坡稳定性系数跟降雨强度有很大关系，滑坡发生蠕动失稳的主要原因是，入渗的雨水导致地下水位线上升，滑动的抗剪强度大大降低。在年均降雨强度下，滑坡中水场变化不大，在遇到强暴雨情况下，水势场有明显的变化。

3) 林达滑坡主滑体1#次级滑体在暴雨状况下处于基本稳定–稳定状态。在遇到极端暴雨天气或者持续暴雨情况下，滑坡有发生滑动的可能，滑坡急需治理；在天然状况下处于稳定状态，不用担心其滑坡隐患。

6.2. 建议

1) 本文在确定滑带土的抗剪强度参数时选择的是工程类比法，主观性很强。所以建议根据滑坡的宏观变形状况先假设滑坡的滑动面范围以及稳定性系数，反算滑带土抗剪强度参数，然后与工程类比所得的相比较再综合确定其取值。

2) 乐安水电站水库区气候湿润，雨水充沛且暴雨不在少数。因此为了减少自然因素对滑坡的影响，可以采取一些相应保护措施如：设置截排水沟、排水盲沟，防止地表水、地下水流入滑体内。

3) GeoStudio软件只能计算二维模型，不能很好的刻画渗流场、应力场以及应力突变在空间上的变化情况，具有局限性，宜选用三维模拟如Flac3d分析会更具有客观性。

NOTES

^*通讯作者。