给定度序列具有最小覆盖成本的树

doi:10.12677/AAM.2021.107270

期刊菜单

给定度序列具有最小覆盖成本的树
The Minimum Cover Cost of a Tree with Given Degree Sequence

DOI: 10.12677/AAM.2021.107270, PDF, HTML, XML,
作者: 贾雁宇, 李玉瑛^*, 郝艺方：太原理工大学数学学院，山西晋中
关键词: 度序列；覆盖成本；贪婪树；Degree Sequence； Cover Cost； Greedy Tree

摘要: 图G上顶点v的覆盖成本定义为

，H_vu是从v开始随机游走到达u的平均首达时间。本文研究了给定度序列树的覆盖成本，并且刻画出覆盖成本最小的树。

Abstract: The cover cost of a vertex v in G is defined as

, where H_vu is the expected hitting time for random walk beginning at v to visit u. In this paper, we study the cover cost of trees and characterize the unique tree with the minimum cover cost with given degree sequence.

文章引用：贾雁宇, 李玉瑛, 郝艺方. 给定度序列具有最小覆盖成本的树[J]. 应用数学进展, 2021, 10(7): 2605-2613. https://doi.org/10.12677/AAM.2021.107270

1. 引言

设G为具有顶点集 $V (G) = {v_{1}, v_{2}, \dots, v_{n}}$ 和边集 $E (G)$ 的简单连通图。任给 $v \in V (G)$ ，v的度是与v关联的边的数目，用 $d (v)$ 表示。令 $d (v_{i}) = d_{i}, i = 1, 2, \dots, n$ ，则非增序列 $π = (d_{1}, d_{2}, \dots, d_{n})$ 称为G的度序

列。图G中度至少为3的顶点称为分支点，度为1的顶点称为叶子点或者悬挂点。

Wiener指数是指图G的所有顶点对的距离和，即 $W (G) = \sum_{{u, v} \subseteq V (G)} d_{G} (u, v) = \frac{1}{2} \sum_{v \in V (G)} D_{G} (v)$ ，这里 $D_{G} (v) = \sum_{u \in V (G)} d_{G} (v, u)$ 。直到现在，Wiener指数在各种图族中被广泛研究，一些结论可以在 [1] [2] [3]

中找到。

我们称树 $(T, r)$ 是以顶点r为根的树，在这个有根树中， $P_{T} (v, u)$ 表示树T中连通顶点 $v, u$ 的唯一路， $d_{T} (v, u)$ 为路 $P_{T} (v, u)$ 上边的数目，顶点v的高度定义为 $h_{T} (v) = d_{T} (r, v)$ 。在 $(T, r)$ 中，对于任意两个不同的顶点 $u, v$ ，如果 $P_{T} (r, u) \subset P_{T} (r, v)$ ，称v是u的后序点，u是v的前序点。如果v和u相邻且 $d_{T} (r, u) = d_{T} (r, v) - 1$ ，称u是v的parent，v是u的child。如果两个顶点 $u, v$ 有同一个parent，则称 $u, v$ 是

siblings。

2008年，Wang Hua [2] 刻画出给定度序列使Wiener指数最小化的树是贪婪树。2012年，Georgakopoulos

[4] 在图G中定义了顶点v的覆盖成本 $C C_{G} (v)$ 是从v开始随机游走到达图中所有顶点的平均首达时间总和，即 $C C_{G} (v) = \sum_{u \in V (G)} H_{v u}$ ，并研究了覆盖成本的性质。2015年，Georgakopoulos和Wagner [5] 在图G中定义了顶点v的反向覆盖成本 $R C_{G} (v) = \sum_{u \in V (G)} H_{u v}$ ，并且得到了树的覆盖成本与Wiener指数关系的公式以及反向覆盖成本与Wiener指数关系的公式，即对于树T和任给 $v \in V (T)$ ，有

$C C_{T} (v) = 2 W (T) - D_{T} (v)$ ，

$R C_{T} (v) = (2 n - 1) D_{T} (v) - 2 W (T)$ 。

他们确定了给定阶数树的覆盖成本，反向覆盖成本和首达时间的极值和极图。2019年，李书超和王书晶 [6] 在给定片段序列的情况下，刻画出覆盖成本最小及反向覆盖成本最小的树，也找到了反向覆盖成本最大的唯一树。2021年，张慧慧和李书超 [7] 在给定直径，匹配数和控制数的情况下，得出覆盖成本和反向覆盖成本的上下界，并刻画了对应的极图。

基于以上研究，本文在给定度序列的情况下，刻画出覆盖成本最小的树。

2. 预备知识

下面介绍本文用到的一些定义和定理。

定理2.1 [5]. 对于树T和任给 $v \in V (T)$ ，有

$C C_{T} (v) = 2 W (T) - D_{T} (v)$ ,

$R C_{T} (v) = (2 n - 1) D_{T} (v) - 2 W (T)$ .

定义集合 $L (T) = {v \in V (T) | D_{T} (v) \geq D_{T} (u), \forall u \in V (T)}$ 。

定理2.2 [6]. 任给树T， $v \in V (T)$ 当且仅当 $C C_{T} (v) = \min_{u \in V (T)} C C_{T} (u)$ 当且仅当 $R C_{T} (v) = \max_{u \in V (T)} R C_{T} (u)$ 。任给 $v \in V (T)$ ，v是悬挂点。

定义2.1 [2]. 给定非叶子点的度，贪婪树通过下面的贪婪算法得到：

1) 将最大度的顶点命名为v (根)；

2) 将与v相邻的顶点依次命名为 $v_{1}, v_{2}, \dots$ ，给这些顶点分配可用的最大度且满足 $d (v_{1}) \geq d (v_{2}) \geq \dots$ ；

3) 将与 $v_{1}$ 相邻的顶点依次命名为 $v_{11}, v_{12}, \dots$ (v除外)，给这些点分配可用的最大度且满足 $d (v_{11}) \geq d (v_{12}) \geq \dots$ ，顶点 $v_{2}, v_{3}, \dots$ 做法类似。

4) 对所有新命名的顶点重复3)，总是从已命名且度最大的顶点的未命名邻集开始。

从上面的定义中可以得出贪婪树的性质如下：

定理2.3 [2]. 给定度序列的有根树T是贪婪树，如果满足下面条件：

1) 根v具有最大度；

2) 任意两个叶子点的高度差至多是1；

3) 对于任意两个顶点u和w，如果 $h_{T} (w) < h_{T} (u)$ ，则 $d (w) \geq d (u)$ ；

4) 对于有相同高度的任意两个顶点 $u, w$ ，如果 $d (u) > d (w)$ ，则 $d (u^{'}) \geq d (w^{'})$ ， $u^{'}, w^{'}$ 分别是 $u, w$ 的后序点， $u^{'}$ 和 $w^{'}$ 高度相同；

5) 对于有相同高度的任意两个顶点 $u, w$ ，如果 $d (u) > d (w)$ ，则 $d (u^{'}) \geq d (w^{'})$ ， $d (u^{″}) \geq d (w^{″})$ ， $u^{'}, w^{'}$ 分别是 $u, w$ 的siblings， $u^{″}, w^{″}$ 分别是 $u^{'}, w^{'}$ 的后序点， $u^{'}$ 和 $w^{'}$ 高度相同， $u^{″}$ 和 $w^{″}$ 高度相同。

例1．度序列为 $(4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 2, 2, 1, \dots, 1)$ (1的重数为15)的贪婪树如图1所示。

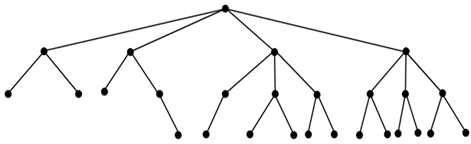
Figure 1. Greedy tree with degree sequence of (4,4,4,3,3,3,3,3,3,3,2,2,1,…,1)

图1. 度序列为(4,4,4,3,3,3,3,3,3,3,2,2,1,…,1)的贪婪树

3. 主要结论

本节研究给定度序列树的覆盖成本，并且称该条件下覆盖成本最小的树是理想树。

在理想树中选一条路，移除这条路上的所有边之后，如果一些连通分支仍然存在，取一个点将其命

名为z，将点z右边的顶点依次命名为 $x_{1}, x_{2}, \dots$ ，将点z左边的顶点依次命名为 $y_{1}, y_{2}, \dots$ 。令 $X_{i}, Y_{i}, Z (i = 1, 2, \dots)$ 表示包含对应顶点的分支， $X_{> k}$ 和 $Y_{> k}$ 分别表示由 $V (X_{k + 1}) \cup V (X_{k + 2}) \cup \dots$ 和 $V (Y_{k + 1}) \cup V (Y_{k + 2}) \cup \dots$ 导出的子树，如图2。不失一般性，假设 $| V (X_{1}) | \geq | V (Y_{1}) |$ 。

Figure 2. The components resulted from a path with z

图2. 带有顶点z的路产生的分支

定理3.1. 在如上描述的情形中，对于 $i = 1, 2, \dots, k$ ，如果有 $| V (X_{i}) | \geq | V (Y_{i}) |$ ，则在理想树中满足 $| V (X_{> k}) | \geq | V (Y_{> k}) |$ 。

证明：假设在理想树中 $| V (X_{> k}) | \geq | V (Y_{> k}) |$ 不成立，下面证明交换 $X_{> k}$ 和 $Y_{> k}$ 的位置不增加覆盖成本。当路的末端顶点都在或都不在 $V (Y_{> k}) \cup V (X_{> k})$ 中，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，这两点之间的距离不会改变。因此考虑只有一个末端顶点在 $V (Y_{> k}) \cup V (X_{> k})$ 的情况。

先计算 $W (T^{'}) - W (T)$ ，分为下面四种情况：

1) 对于 $V (X_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和 $X_{> k}$ 中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离增加2i，则总的Wiener指数增加 $\sum_{i = 1}^{k} (2 i) | V (X_{i}) | | V (X_{> k}) |$ ；

2) 对于 $V (Y_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和 $X_{> k}$ 中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离减少2i，则总的Wiener指数减少 $\sum_{i = 1}^{k} (2 i) | V (Y_{i}) | | V (X_{> k}) |$ ；

3) 对于 $V (Y_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离减少2i，则总的Wiener指数减少 $\sum_{i = 1}^{k} (2 i) | V (Y_{i}) | | V (Y_{> k}) |$ ；

4) 对于 $V (X_{i}) (i = 1, 2, \dots, k)$ 中的任一顶点和 $Y_{> k}$ 中的任一顶点，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，两点之间的距离增加2i，则总的Wiener指数增加 $\sum_{i = 1}^{k} (2 i) | V (X_{i}) | | V (Y_{> k}) |$ ；

综上分析，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，得出 $W (T^{'}) - W (T) = \sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |) (| V (X_{> k}) | - | V (Y_{> k}) |)$ 。

根据定理2.2，令 $C C_{T} (x) = \min_{v \in V (T)} C C_{T} (v)$ ，则 $x \in L (T)$ 。

情形1： $x \in V (X_{i}) (1 \leq i \leq k)$

此时， $D_{T^{'}} (x) - D_{T} (x) = 2 i (| V (X_{> k}) | - | V (Y_{> k}) |)$ ，利用引理2.1可得

$\begin{array}{l} C C_{T^{'}} (x) - C C_{T} (x) = 2 (W (T^{'}) - W (T)) - (D_{T^{'}} (x) - D_{T} (x)) \\ = 2 (| V (X_{> k}) | - | V (Y_{> k}) |) (\sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |) - i) \\ \leq 2 (| V (X_{> k}) | - | V (Y_{> k}) |) \sum_{i = 1}^{k} (2 i (| V (X_{i}) | - | V (Y_{i}) |) - 1) \end{array}$

当 $| V (X_{i}) | = | V (Y_{i}) | (i = 1, 2, \dots, k)$ 时，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，覆盖成本不增加。

存在i使得 $| V (X_{i}) | > | V (Y_{i}) |$ ，则 $\sum_{i = 1}^{k} (2 i (| V (X_{i}) | - | V (Y_{i}) |) - 1) > 0$ ，

由假设 $| V (X_{> k}) | \leq | V (Y_{> k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，最小覆盖成本不增加。

情形2： $x \in V (Y_{i}) (1 \leq i \leq k)$ 与情形1类似。

情形3： $x \in V (X_{> k})$

这时， $D_{T^{'}} (x) - D_{T} (x) = \sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |)$ ，

利用引理2.1化简可得 $C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k} 2 i (| V (X_{i}) | - | V (Y_{i}) |) (2 (| V (X_{> k}) | - | V (Y_{> k}) |) - 1)$ 。

由假设 $| V (X_{> k}) | \leq | V (Y_{> k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以，交换 $X_{> k}$ 和 $Y_{> k}$ 的位置，最小覆盖

成本不增加。

情形4： $x \in V (Y_{> k})$ 与情形3类似。

情形5： $x \in V (Z)$ ， $D_{T^{'}} (x) = D_{T} (x)$ ， $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

综上所述，在理想树中满足 $| V (X_{> k}) | \geq | V (Y_{> k}) |$ ，定理证明完毕。

定理3.2. 在如上描述的情形中，对于 $i = 1, 2, \dots, k - 1$ ，有 $| V (X_{i}) | \geq | V (Y_{i}) |$ ， $| V (X_{> k}) | \geq | V (Y_{> k}) |$ ，则在理想树中满足 $| V (X_{k}) | \geq | V (Y_{k}) |$ 。

证明：假设在理想树中， $| V (X_{k}) | \geq | V (Y_{k}) |$ 不成立，下面证明交换 $X_{k}$ 和 $Y_{k}$ 的位置不会增加覆盖成本。

根据定理2.2，令 $C C_{T} (x) = \min_{v \in V (T)} C C_{T} (v)$ ，则 $x \in L (T)$ 。

经过计算得 $\begin{matrix} W (T^{'}) - W (T) = \sum_{i = 1}^{k - 1} 2 i (| V (X_{i}) | - | V (Y_{i}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ + 2 k (| V (X_{> k}) | - | V (Y_{> k}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ \leq 0 \end{matrix}$

情形1： $x \in V (X_{i}) (1 \leq i \leq k - 1)$

$\begin{matrix} C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (X_{i}) | - | V (Y_{i}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ + 4 k (| V (X_{> k}) | - | V (Y_{> k}) |) (| V (X_{k}) | - | V (Y_{k}) |) \\ - 2 i (| V (X_{k}) | - | V (Y_{k}) |) \end{matrix}$

由假设 $| V (X_{k}) | \leq | V (Y_{k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以交换 $X_{k}$ 和 $Y_{k}$ 的位置，最小覆盖成本

不增加。

情形2： $x \in V (Y_{i}) (1 \leq i \leq k - 1)$ 与情形1类似。

情形3： $x \in V (X_{> k})$

$C C_{T^{'}} (x) - C C_{T} (x) = (\sum_{i = 1}^{k - 1} 4 i (| V (X_{i}) | - | V (Y_{i}) |) + 4 k (| V (X_{> k}) | - | V (Y_{> k}) |) - 2 k) (| V (X_{k}) | - | V (Y_{k}) |)$

由假设 $| V (X_{k}) | \leq | V (Y_{k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

又因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以交换 $X_{k}$ 和 $Y_{k}$ 的位置，最小覆盖成

本不增加。

情形4： $x \in V (Y_{> k})$ 与情形3类似。

情形5： $x \in V ( X k )$

$\begin{matrix} C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} (| V (X_{i}) | - | V (Y_{i}) |) (4 i (| V (X_{k}) | - | V (Y_{k}) |) - 1) \\ + (| V (X_{> k}) | - | V (Y_{> k}) |) (4 k (| V (X_{k}) | - | V (Y_{k}) |) - 1) \end{matrix}$

由假设 $| V (X_{k}) | \leq | V (Y_{k}) |$ ，可得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

又因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以交换 $X_{k}$ 和 $Y_{k}$ 的位置，最小覆盖成

本不增加。

情形6： $x \in V (Y_{k})$ 与情形5类似。

情形7： $x \in V (Z)$ ， $D_{T^{'}} (x) = D_{T} (x)$ ， $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

综上所述，在理想树中满足 $| V (X_{k}) | \geq | V (Y_{k}) |$ ，定理证明完毕。

定理3.3. 在如上描述的情形中，对于 $i = 1, 2, \dots, k - 1$ ，如果有 $| V (X_{i}) | \geq | V (Y_{i}) |$ 和 $| V (X_{> k - 1}) | \geq | V (Y_{> k - 1}) |$ 成立，则在理想树中满足 $d (x_{k}) \geq d (y_{k})$ 。

证明：假设在理想树中 $d (x_{k}) \geq d (y_{k})$ 不成立，设 $a = d (x_{k}) < d (y_{k}) = a + b$ ，从 $X_{k} (Y_{k})$ 中移除顶点 $x_{k} (y_{k})$ 会产生 $a (a + b)$ 个分支。从 $Y_{k}$ 中任取b个分支(令B为b个分支)，将这些分支与顶点 $x_{k}$ 连接。经过此操作有 $d (x_{k}) \geq d (y_{k})$ ，且度序列不改变。

根据定理2.2令 $C C_{T} (x) = \min_{v \in V (T)} C C_{T} (v), x \in L (T)$ 。

计算得 $W (T^{'}) - W (T) = \sum_{i = 1}^{k - 1} 2 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 2 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B |$

情形1： $x \in V (X_{i}) (1 \leq i \leq k - 1)$

$C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 4 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B | + 2 i | B |$

由已知可以得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，经过上面操作，最小覆盖成本不增加。

情形2： $x \in V (Y_{i}) (1 \leq i \leq k - 1)$ 与情形1类似。

情形3： $x \in V (Y_{> k - 1} - B)$

$C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 4 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B | - 2 k | B |$

由已知可以得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以经过上面操作，最小覆盖成本不增加。

情形4： $x \in V (X_{> k - 1})$ 与情形3类似。

情形5： $x \in V ( B )$

$\begin{matrix} C C_{T^{'}} (x) - C C_{T} (x) = \sum_{i = 1}^{k - 1} 4 i (| V (Y_{i}) | - | V (X_{i}) |) | B | + 4 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) | B | \\ - \sum_{i = 1}^{k - 1} (2 i) (| V (Y_{i}) | - | V (X_{i}) |) - 2 k (| V (Y_{> k - 1}) | - | B | - | V (X_{> k - 1}) |) \end{matrix}$

由已知可以得出 $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

因为 $\min_{v \in V} C C_{T^{'}} (v) \leq C C_{T^{'}} (x) \leq C C_{T} (x) = \min_{v \in V} C C_{T} (v)$ ，所以经过上面操作，最小覆盖成本不增加。

情形6： $x \in V (Z)$ ， $D_{T^{'}} (x) = D_{T} (x)$ ， $C C_{T^{'}} (x) - C C_{T} (x) \leq 0$ 。

综上所述，在理想树中满足 $d (x_{k}) \geq d (y_{k})$ ，定理证明完毕。

在理想树中选一条最长路，将各个顶点依次命名为 $w_{1}, w_{2}, \dots$ 和 $u_{1}, u_{2}, \dots$ ，将各个点所在的分支依次命名为 $W_{i}$ 和 $U_{i}$ ， $U_{1}$ 是拥有点数最多的分支。如图3所示。

Figure 3. The components resulted from a path

图3. 在路上的分支

定理3.4. 如上面所述，在理想树中，如果路长是奇数 $2 m - 1$ ，则有

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (U_{m}) | = | V (W_{m}) | = 1$ ;

如果路长是偶数2m，则有 $| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (W_{m}) | = | V (U_{m + 1}) | = 1$ ；

证明：本定理只证明路长为奇数，路长为偶数可类似证明。我们假设 $| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) |$ 。对

于某个k，我们可得

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (W_{k - 1}) | \geq | V (U_{k}) |$ (1)

如果(1)中除了 $| V (U_{k}) | \geq | V (W_{k}) |$ 其余都成立。我们可以交换 $W_{i}$ 和 $U_{i}$ 的命名去保证 $| V (U_{k}) | \geq | V (W_{k}) |$ (如果有必要)。否则，根据定理3.1可得 $| V (U_{> k - 1}) | \geq | V (W_{> k - 1}) |$ 。

如果 $| V (W_{k}) | \geq | V (U_{k}) |$ ，则可以得出

$| V (U_{> k}) | = | V (U_{> k - 1}) | - | V (U_{k}) | > | V (W_{> k - 1}) | - | V (W_{k}) | = | V (W_{> k}) |$

应用定理3.2 (令 $x_{i} = u_{i}, y_{i} = w_{i}, i = 1, 2, \dots$ )，由 $| V (U_{> k}) | \geq | V (W_{> k}) |$ ，会得出 $| V (U_{k}) | \geq | V (W_{k}) |$ ，与前面假设 $| V (W_{k}) | \geq | V (U_{k}) |$ 矛盾。因此，可以得出

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (U_{k}) | \geq | V (W_{k}) |$ .

如果所有的不等式成立，可以交换 $U_{i + 1}, W_{i}$ 去保证 $| V (W_{k}) | \geq | V (U_{k + 1}) |$ (如果有必要)。否则，对 $U_{> k}$ 和 $W_{> k - 1}$ 应用定理3.1，令 $Z = U_{1}, Y_{i} = U_{i + 1}, X_{i} = W_{i}, z = u_{1}, y_{i} = u_{i + 1}, x_{i} = w_{i}$ ，有 $| V (X_{i}) | \geq | V (Y_{i}) | (i = 1, 2, \dots, k - 1)$ ，由定理3.1可得

$| V (W_{> k - 1}) | = | V (X_{> k - 1}) | \geq | V (Y_{> k - 1}) | = | V (U_{> k}) |$

如果 $| V (Y_{k}) | = | V (U_{k + 1}) | > | V (W_{k}) | = | V (X_{k}) |$ ，则有

$| V (Y_{> k}) | = | V (Y_{> k - 1}) | - | V (Y_{k}) | < | V (X_{> k - 1}) | - | V (X_{k}) | = | V (X_{> k}) |$ ,

对 $Y_{k} = U_{k + 1}, X_{k} = W_{k}$ 应用定理3.2，可得 $| V (X_{k}) | > | V (Y_{k}) |$ ，与前面假设 $| V (Y_{k}) | > | V (X_{k}) |$ 矛盾，因此，有

$| V (U_{1}) | \geq | V (W_{1}) | \geq | V (U_{2}) | \geq | V (W_{2}) | \geq \dots \geq | V (U_{k}) | \geq | V (W_{k}) | \geq | V (U_{k + 1}) |$ .

定理3.5. 如上面所述，在理想树中，如果路长是奇数 $2 m - 1$ ，则有

$d (u_{1}) \geq d (w_{1}) \geq d (u_{2}) \geq d (w_{2}) \geq \dots \geq d (u_{m}) = d (w_{m}) = 1$ ;

如果路长是偶数2m，则有

$d (u_{1}) \geq d (w_{1}) \geq d (u_{2}) \geq d (w_{2}) \geq \dots \geq d (w_{m}) = d (u_{m + 1}) = 1$ ;

证明：本定理只证明路长为奇数，路长为偶数时可类似证明。对 $u_{i}, u_{i + 1} (i = 1, 2, \dots, m - 1)$ 应用定理3.3，令 $y_{1} = u_{i + 1}, y_{2} = u_{i + 2}, \dots; x_{1} = u_{i}, x_{2} = u_{i - 1}, \dots, x_{i} = u_{1}, x_{i + 1} = w_{1}$ 。则

$| V (X_{> 1}) | = \sum_{k = 1}^{m} | V (W_{k}) | + \sum_{k = 1}^{i - 1} | V (U_{k}) | > \sum_{k = i + 2}^{m} | V (U_{k}) | = V (Y_{> 1})$ ,

推出 $d (u_{i}) = d (x_{1}) \geq d (y_{1}) = d (u_{i + 1})$ 。因此，可以得出

$d (u_{1}) \geq d (u_{2}) \geq \dots \geq d (u_{m})$ .

同理，对 $w_{i}, w_{i + 1}$ 应用定理3.3，得出 $d (w_{1}) \geq d (w_{2}) \geq \dots \geq d (w_{m})$ 。

对于 $u_{i}, w_{i}$ ，如果定理3.4中的不等式处处成立，可得 $d (u_{i}) \geq d (w_{i}) (i = 1, 2, \dots, m)$ 。否则，给 $u_{i}, w_{i}$ 应用定理3.3(令 $x_{i} = u_{i}, y_{i} = w_{i}, i = 1, 2, \dots$ )得出 $d (u_{i}) \geq d (w_{i}) (i = 1, 2, \dots, m)$ 。

相似的，给 $w_{i}, u_{i + 1}$ 应用定理3.3，得出 $d (w_{i}) \geq d (u_{i + 1}) (i = 1, 2, \dots, m - 1)$ 。

定理3.6. 具有最小覆盖成本的树是贪婪树。

证明：在任意一条路中， $D_{T} (v)$ 只在一个顶点或者两个相邻的顶点取到最小值，称这些点为重心。在定理3.4，3.5的理想树中的任意一条路上， $D_{T} (v)$ 在 $u_{1}$ 处取到最小值， $d (u_{1})$ 和 $| V (U_{1}) |$ 在这条路上都是最大的。

下面有两种情况：

1) 如果重心为一个点，则命名为v。

2) 如果重心为两个点，则两个分支(移除两个顶点之间的边)有相同的顶点数。选择其中一个顶点命名为v，另一个命名为 $v_{1}$ ，

本文只证明第一种情况，第二种情况证明类似。

在以顶点v为根的理想树 $(T, v)$ 中，很容易得出v是具有最大度的顶点。(引理2.3中(1)满足)

考虑任意一条以叶子点u开始，经过顶点v，以叶子点w结束(w和u有唯一相同的前序点v)的路，在这条路上应用定理3.5，使 $u_{1} = v$ ，可以得出

$| d_{T} (u, v) - d_{T} (w, v) | \leq 1$ ，即任意两个叶子点的高度差至多是1。(引理2.3中(2)满足)

并且，可以推出对于任意两个顶点 $x, y$ (y是x的后序点)，都有 $d (x) \geq d (y)$ 。

对于高度为i的顶点x和高度为j的顶点y ( $i < j$ )，考虑下面两种情况：

a) 如果y是x的后序点，可直接由上面得出 $d (x) \geq d ( y )$

b) 否则，令u为 $x, y$ 共同的前序点，且顶点u在 $P_{T} (x, y)$ 上。在通过顶点 $y^{'}, y, u, x, x^{'}$ 的路上应用定理3.5 ( $y^{'}, x^{'}$ 分别为 $y, x$ 的后序点，且为叶子点)，有 $u_{1} = u$ ，由定理3.4可知

$x = u_{k + 1}, y = w_{l}$ 或者 $x = w_{k}, y = u_{l + 1}, (k = i - h_{T} (u), l = j - h_{T} (u), k + 1 \leq l)$ ，

根据定理3.5可推出 $d (x) \geq d (y)$ 。(引理2.3中(3)满足)

对于两个相同高度的非叶子点 $x, y$ ，满足 $d (x) \geq d (y)$ 。 $y^{'}, x^{'}$ 分别为 $y, x$ 的后序点，在通过顶点 $y^{'}, y, u, x, x^{'}$ 的最长路上应用定理3.5 (u为 $x, y$ 共同的前序点，且顶点u在 $P_{T} (x, y)$ 上)，有 $u_{1} = u$ ，根据定理3.4有，

$x = w_{k}, x^{'} = w_{l}, y = u_{k + 1}, y^{'} = u_{l + 1}, (k = i - h_{T} (u), l = j - h_{T} (u))$ ,

因此可以推出

$d (x^{'}) \geq d (y^{'})$ 。(引理2.3中(4)满足)

令 $x_{0} (x^{'}), y_{0} (y^{'})$ 分别为 $x, y$ 的parents (siblings)，令 $y^{″}, x^{″}$ (高度为j)分别为 $y^{'}, x^{'}$ 的后序点，由结论(4)可推出 $| V (T (x_{0}) / T (x^{'})) | > | V (T (y_{0}) / T (y^{'})) |$ 。现在考虑经过顶点 $y^{″}, y^{'}, u, x^{'}, x^{″}$ 的最长路，u为 $x, y$ 共同的前序点且顶点u在 $P_{T} (x, y)$ 上，应用定理3.5则有 $u_{1} = u$ ，由定理3.5有 $x^{'} = w_{k}, x^{″} = w_{l}, y^{'} = u_{k + 1}, y^{″} = u_{l + 1}, (k = i - h_{T} (u), l = j - h_{T} (u))$ ，

因此可以推出

$d (x^{'}) \geq d (y^{'}), d (x^{″}) \geq d (y^{″})$ 。(引理2.3中(5)满足)

从而覆盖成本最小的树是贪婪树，即理想树是贪婪树，定理证明完毕。

例2．度序列为 $(4, 4, 3, 3, 3, 3, 2, 2, 1, \dots, 1)$ (1的重数为10)时，覆盖成本最小的树即贪婪树，如图4所示。

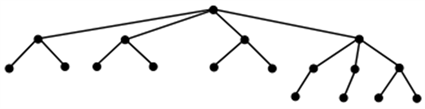
Figure 4. Greedy tree with degree sequence of (4,4,3,3,3,3,2,2,1,…,1)

图4. 度序列为(4,4,3,3,3,3,2,2,1,…,1)的贪婪树

NOTES

^*通讯作者。

参考文献

[1]	Fischermann, M., Hoffmann, A., Rautenbach, D., Székely, L. and Volkmann, L. (2002) Wiener Index versus Maximum Degree in Trees. Discrete Applied Mathematics, 122, 127-137.
[2]	Wang, H. (2008) The Extremal Values of the Wiener Index of a Tree with Given Degree Sequence. Discrete Applied Mathematics, 156, 2647-2654.
[3]	Zhang, X.D., Xiang, Q.Y., Xu, L.Q. and Pan, R.Y. (2008) The Wiener Index of Trees with Given Degree Sequences. Match-Communications in Mathematical and in Computer Chemistry, 60, 623-644.
[4]	Georgakopoulos, A. (2012) A Tractable Variant of Cover Time. arXiv:1206.6605.
[5]	Georgakopoulos, A. and Wagner, S. (2017) Hitting Times, Cover Cost, and the Wiener Index of a Tree. Journal of Graph Theory, 84, 311-326.
[6]	Li, S.C. and Wang, S.J. (2020) Extremal Cover Cost and Reverse Cover Cost of Trees with Given Segment Sequence. Discrete Mathematics, 343, 111791.
[7]	Zhang, H.H. and Li, S.C. (2021) On the (Reverse) Cover Cost of Trees with Some Given Parameters. Discrete Mathematics, 344, 112226.

为你推荐

友情链接