无线可充电传感器网络充电规划模型构建

Charging Programming Modelling and Construction of Wireless Rechargeable Sensor Networks

摘要: 随着无线可充电传感器网络(Wireless Rechargeable Sensor Network, WRSN)在社会生活中的应用越来越广泛，如何制定充电策略来应对更加灵活的充电场景是一个值得研究的问题。首先，本文规划出移动充电器(Mobile Charger, MC)移动路径能量消耗最少的单MC充电策略，在此基础上提出了周期演绎充电模型(Periodic Deductive Charging, PDC)和稳定系统充电模型(Stabilizing System Charging, SSC)，给出了单MC工作的最小电池容量(Minimum Battery Capacity, MBC)的计算方法。然后，结合实际充电场景，分别构建了基于遗传算法和最小电池容量(Minimum Battery Capacity-Genetic Algorithm, MBC-GA)的多MC路线规划模型及支持增加传感器的SSC和多MC模型，得到充电器和传感器数量增加时的路线规划及此时的传感器MBC。最后，通过实例进一步验证了模型的原理，结果证明所提出的模型能有效求解出不同条件下整个系统稳定运行的传感器MBC。

Abstract: With the more and more extensive application of wireless rechargeable sensor network (WRSN) in social life, how to formulate charging strategy to deal with more flexible charging scenarios is a problem worthy of research. Firstly, this paper plans a single mobile charger (MC) charging strategy with the least energy consumption in the mobile path of MC. On this basis, periodic deductive charging (PDC) model and stabilizing system charging (SSC) model are proposed, and the calculation method of minimum battery capacity (MBC) of single MC is given. Then, combined with the actual charging scenario, the Multi MC route planning model based on genetic algorithm and minimum battery capacity genetic algorithm (MBC-GA) and the SSC and Multi MC model supporting the addition of sensors are constructed respectively to obtain the route planning when the number of chargers and sensors increases and the sensor MBC at this time. Finally, the principle of the model is further verified by an example. The results show that the proposed model can effectively solve the sensor MBC of the whole system under different conditions.

1. 引言

无线传感器网络(Wireless Sensor Network, WSN)是物联网(Internet of Things, IoT)的常用核心部件之一，具有广阔的应用前景和较高的商业价值。然而，传统WSN电池受容量有限，生命周期较短，更换成本高等制约，进一步应用受到影响。而无线可充电传感器网络WRSN能够利用移动式充电器MC定期为传感器补充能量，保证其正常运转，具有良好的应用发展前景。目前关于WRSN的研究主要有WSN协议设计研究和充电规划研究两个方面 [1]。其中充电规划研究着重于MC移动路径规划 [2] [3] [4]，多充电器间充电协调策略 [4] 等研究方向。MC移动路径规划主要考虑在不同预设目标下对MC的移动充电路径进行规划。常见的目标如考虑移动路径上的充电器能量消耗最小化问题，这类问题通常可等价为旅行商问题(TSP)。旅行商问题是组合优化领域中著名的NP-Hard问题，分为单旅行商问题和多旅行商问题(MTSP)，已有求解算法包括适用于求解小规模TSP问题的精确算法，可得到次优解的启发式算法，现代智能算法以及机器学习方法等。目前应用最广泛的是智能算法，如遗传算法(GA) [5]，蚁群算法(ACA) [6] [7] [8]，模拟退火算法(SA) [9]，禁忌搜索算法(TSA) [10] 等，另外也不乏不同算法的结合应用 [11] [12] [13]，单/多MC充电策略方面，现有研究成果主要分为一对一和一对多充电两种模式。王杨等人探讨了一对一充电模式下，从MC调度，传感器充电时间分配，节点速度控制协同优化来提高网络性能 [14]。潘琪等人提出了一对多充电方式下WRSN中MC驻点选择策略 [15]。何聪提出了不限容量单MC的定向充电规划和容量受限多MC的定向充电规划系统模型，并设计启发式算法实现较高充电效率 [16]。

WRSN中每个传感器都有特定的能量消耗速率和固定的电池容量，要保证WRSN正常运行，MC需定期为传感器充电，从而在不同设定目标下去进行充电路线规划。本文在已知各个传感器节点的位置信息，消耗速率，MC移动路径，MC移动速度，MC充电速率以及传感器的最小工作阈值等信息的条件下，先以MC充电路径上能量消耗最少为目标进行充电路径规划，在此基础上，分别探讨了满足传感器最小容量的单充电器(Single Mobile Charger, SM)充电策略和多充电器(Multiple Mobile Chargers, MM)充电策略，求解出能保证整个系统正常运行的传感器MBC。此外，当前研究对充电场景有较多理想化的假设，对某些特殊场景关注不够，很少涉及传感器数量变化的应对策略，然而在实际生活中传感器需求日益增加，常常需要增设若干传感器以灵活地应对充电场景的改变。因此本文进而也探讨了在不改变原有传感器位置分布及属性特点的基础上，临时增加传感器所对应的单MC和多MC最优充电路径策略，以及求解新增传感器的MBC。最后本文通过一个实证验证了上述模型的有效性。

2. 问题阐述和方法研究

WRSN主要由一个数据中心DC，若干传感器和一个或多个移动充电器MC三部分组成。传感器与数据中心进行着信息的传输，WRSN中每个传感器都有特定的能量消耗速率和固定的电池容量，要保证WRSN正常运行，MC需定期为传感器的电池进行充电以避免其电量低于运行最低阈值，完成全部传感器的充电任务即完成一个充电周期。从数学上理解，WRSN系统的一个充电周期指的是MC从DC出发，遍历全部 个传感器进行充电后再次回到DC所花的时间。WRSN充电路径工作原理如图1所示(虚线箭头表示存在互相连通的路径，实线箭头表示充电路线)。

移动充电器定期为传感器的电池进行充电以保证整个无线可充电传感器网络的正常运转。若数据中心和传感器分布在一个二维空间中，则分布方式如图1所示(虚线箭头表示存在一条互相连通的路径，实线箭头表示充电路线)。

本文研究工作具体包括：

1) 充电路径能量消耗最小的单MC和多MC的充电路径规划

充电路径的能量消耗主要有两个方面：一是为传感器节点充电所导致的正常的能量消耗，在环境系统参数不变的情况下，此部分只与转移路径距离成正比，另外则是MC在转移路径上的能量消耗。路径规划的目的通常就是优化转移路径。这时，单MC的路径规划问题通常可视为经典的TSP问题，可以用较为简便的改良圈算法与精度较高的遗传算法结合寻求最短路径。改进后的算法在求解精度上比单一算法有所提升，且迭代次数能显著减少，而对于多MC充电路径规划的MTSP问题，可运用遗传算法，并考虑多MC工作量和传感器间电池容量的均衡等问题，得到每个MC的具体路线规划。为下面表述方便，不妨设所得的单MC充电路线按顺时针方向记为 $DC\to S_1\to S_2\to S_3\to \cdots \to S_{n-1}\to S_n\to DC$。

2) 单MC的传感器电池最小工作容量计算

当一个传感器的电池容量低于一个阈值时，WRSN便无法进行正常的信息采集工作，这个阈值被称为传感器电池最小工作容量(MBC)。为了让WRSN正常运转，MC需要定期为传感器进行充电以避免传感器的电池低于其MBC。因此，要求MC在最短路径下完成一个充电周期时，每一个传感器剩余电池容量恰好不低于MBC，即为模型目标。

Figure 1. Working principle of charging path on WRSN

图1. WRSN充电路径工作原理

每个传感器与数据中心的距离均不同，因此每个传感器在MC到达前的消耗并不相同，以周期为单位进行计算，可计算出MC从数据中心DC出发依次经过规划路线时各个传感器电量的消耗情况。计算时，可假定初始状态为满电量，首先计算第1个充电路径周期，之后以第1个周期所用充电时间为基础对第2个充电周期进行讨论，再以第2周期传感器的电量消耗作为参考，可推导出第3个充电周期内每个传感器的电量消耗。以此类推，直到根据第( $N-1$ )个周期计算出第N个周期的电量消耗情况，即建立了周期演绎充电模型(PDC)。以 $S_1,S_2$ 节点为例，前两个周期运行情况如图2所示：

Figure 2. Schematic diagram of charging cycle of the first two sensors

图2. 前两个传感器的充电周期示意图

不考虑意外延迟等因素，在第N周期后，系统进入稳定的充电循环，可建立稳定系统充电模型(SSC)，求解出稳定系统下每个传感器的MBC。

3) 支持增加传感器的单充电器和多充电器策略

在实际场景中，通常会根据需要增设传感器，因此有必要探讨一下传感器数量增加时的路线规划问题，以及充电系统仍保持正常工作时新增传感器的MBC。本文考虑了在SM中原传感器位置和实际MBC不变的前提下，某一周期结束时，在系统中增加若干个新的“满电”传感器，结合上述稳定系统充电模型计算新传感器的MBC。MM问题中，在系统各传感器所属原子回路和实际电池容量及消耗速率都不变的前提下，讨论增加传感器的新路径规划，并计算新增传感器的MBC。

3. 模型建立

3.1. 周期演绎充电模型(PDC模型)

依据已知的最优路径，给定移动充电器移动速度参数即可求得MC在一个周期内处于移动状态时的总时间消耗，按照路线顺序，则可推导出充电时间与充电量关系如式(3.1)：

$\{\begin{array}{l}{t}_{1i}=\frac{x_{1i}}{r-C_i},\\ x_{1i}=\left(\frac{d_{DC\to S_i}}{v}+{\displaystyle \underset{j=0}{\overset{i-1}{\sum }}{t}_{1j}}\right)\ast C_i,i=1,2,\cdots ,n\end{array}$ (3.1)

其中， $t_{1i}\left(i=0,1,\cdots ,n\right)$ 和 $x_{1i}\left(i=1,2,\cdots ,n\right)$ 分别表示第1轮充电周期里给第i个传感器的充电时间和所需充电量，设 $t_{10}=0$ ； $d_{A\to B}$ 代表节点A到节点B的移动距离， $C_i\left(i=1,2,\cdots ,n\right)$ 为第i个传感器能量的消耗速率，r为MC的恒定充电输出速率。

对于第2轮充电周期，利用第1轮所求 $t_{1i}$ 进行推导，类似于第1轮周期，可以得到第2轮的表达式。以此类推，可以推导出第 $N\left(N\ge 2\right)$ 轮充电周期的传感器的充电时间和所需充电量的计算式如式(3.2)所示：

$\{\begin{array}{l}{t}_{Ni}=\frac{x_{Ni}}{r-C_i},\\ x_{Ni}=\left(T_1+{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}{t}_{N-1,j}}+{\displaystyle \underset{j=0}{\overset{i-1}{\sum }}{t}_{N,j}}\right)\ast C_i,\\ t_{Nn}=\frac{x_{Nn}}{r-C_n},\\ x_{Nn}=\left(T_1+{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{t}_{N,j}}\right)\ast C_n.i=1,2,\cdots ,n-1\end{array}$ (3.2)

其中， $T_1$ 为计算TSP所得最短路径下的MC在路径上移动总时间，设 $t_{N0}=0$。

对于任一节点 $S_i$ 而言，第一次等待时间仅为充电器从数据中心出发到达其位置的时间，第二次等待时间为充电器以 $S_i$ 为起点的一个完整充电周期所用时间。时间的增加导致传感器电量消耗增加，进而引发一个循环周期内节点等待时间递增的连锁效应，因此对于每个传感器而言，一定存在一个足够大的电池容量使得其充满电量后足以等到下一次充电，推导可知满足各个传感器正常工作的MBC在经过多周期循环后会收敛于定值，在这个容量下整个充电循环能实现系统稳定运作。此时，每个传感器 $S_i$ 的MBC为 $E_i=x_{Ni}+f$。

3.2. 稳定系统充电模型(SSC模型)

由PDC模型的推导，在运行有限个周期之后充电模式会逐渐趋向一个稳定的充电循环系统，在该稳定系统下，MC到达传感器节点位置时传感器恰好达到最低工作电量，本文建立WRSN的稳定系统充电模型(SSC模型)并求解出稳定系统下每个传感器的MBC。

1) 传感器能量消耗模型

为了更好地结合实际情况进行分析，本模型引入MC在上一周期回到DC后距下一次出发的间隔时间 $t_0$，为简化问题，设该时间为定值，这时MC在非充电状态下消耗的时间即为定值：

$t_d=T_1+t_0.$ (3.3)

稳态时，设MC在每个传感器节点处的充电时长记为 $t_i\left(i=1,2,\cdots ,n\right)$，不影响传感器工作的电池最小阈值记为f。已知每个传感器的电池容量大小为 $E_i$，在非充电时刻，每个传感器节点的能量消耗速率为 $C_i$，则有：

定理3.1每个传感器的电池容量大小可表示为：

$E_i=C_i\left(T_2-t_i+t_d\right)+f\text{.}$ (3.4)

证由条件可知，MC对传感器充电的总时长为：

$T_2={\displaystyle \underset{j=1}{\overset{n}{\sum }}{t}_j}.$ (3.5)

则每个传感器节点在充电之后的能量贮存为：

$e_{zi}=E_i-f.$ (3.6)

则传感器节点维持工作需要消耗的总能量为：

$e_{xi}=C_i\left(T_2-t_i+t_d\right).$ (3.7)

假设MC到达每个节点的充电时刻恰为传感器节点能量到达最小阈值f的时刻，则传感器充满电之后的能量贮存正好满足其维持工作需要的能量消耗，即有：

$e_{zi}=e_{xi}.$ (3.8)

由(3.3)，(3.5)~(3.8)综合，可得证。

2) 传感器的充电模型

传感器在充电时仍存在固定速率的能量消耗，因此在已知传感器充电速率r的条件下，传感器的相对充电速率为：

$c_i=r-C_i.$ (3.9)

又有传感器能量贮存来源于充电接收能量，则有：

$c_i{t}_i=E_i-f.$ (3.10)

3) 周期性移动充电规划模型

基于以上分析，本文建立了周期性移动充电规划模型：

$\{\begin{array}{l}{E}_i-f=C_i\cdot \left(T_2-t_i+t_d\right),\\ c_i{t}_i=E_i-f\text{.}\end{array}$ (3.11)

可以求得以上模型的解析解，得每个传感器的最小电池容量 $E_i$ 和MC在每个传感器处的充电时间 $t_i$ 计算公式如下：

$\{\begin{array}{l}{E}_i=\frac{C_i\left(t_0+T_1\right)\left(r-C_i\right)}{r-C_z}+f,\\ t_i=\frac{C_i\left(t_0+T_1\right)}{r-C_z},\\ C_z={\displaystyle \underset{j=1}{\overset{n}{\sum }}{C}_j}\text{.}\end{array}$ (3.12)

因此，可根据上式计算出SSC模型下每个传感器的MBC和MC在每个传感器处的充电时间。同时由表达式也可以看出，其MBC恰好为某一常数与阈值f的和，也验证了PDC模型的推导。

3.3. 基于MBC-GA-MTSP的多MC路线规划模型

在实际情况中，为了提高充电效率，有时会派出多个充电器进行充电，此时最短路线规划由TSP问题变成MTSP问题。这时，首先考虑分组利用遗传算法求得至少通过不同个数传感器的多MC最短充电路径。进一步考虑不同路径下传感器消耗的电量不同，多MC的最优充电路径不仅仅考虑MC的移动总路程，即充电路径的最小消耗，也要考虑多个MC的工作量均衡，因此综合考虑这些因素得到的最优路线即为基于MBC-GA-MTSP的多MC的最优充电路线。

1) 基于GA-MTSP的多MC最优路线规划

利用遗传算法(GA)求解MTSP问题，在求解最短路径时控制MC至少通过的传感器个数，即可得到基于MBC-GA的多MC路线规划，该路线规划优先考虑MBC的最大值，在MBC最大值相等的情况下选择总路线长度最短的路线规划作为最优路线规划。

对于一个WRSN，我们设派出M个MC为n个传感器进行充电( $M\le n$ )，则由抽屉原理，派出的MC至少通过的传感器个数最大值为：

$k=\left[\frac{n}{M}\right]$ (3.13)

2) 基于MBC最大值考虑的多MC最优路线规划

求解MTSP问题可得到若干条路线，每条路线的MC的路径消耗和充电量同样也只与MC行走的路线长度有关；若对于整个WRSN良性运行，可进而考虑整体的协调和均衡。因此，可从MBC均衡角度考虑MTSP的分组选择。由(3.12)可计算每天线路下传感器的MBC。若有n个传感器的WRSN系统得到 $k\left(k\le K\right)$ 种可能的分组充电策略，将传感器MBC最大值最小的分组方案记入集合S中，即：

$S=\left\{i|\underset{1\le i\le k}{\min }\underset{1\le j\le n}{\max }{E}_{ij},i,j\in Z\right\}$ (3.14)

其中， $E_{ij}$ 表示第i中路线下第j个传感器的MBC。

将数据代入(3.14)式即可求出集合S。对于集合S下对应的若干条路线，我们选择总路线长度最短的路线作为最优路线，即同时满足(3.14)和(3.15)对应的路线，其中， $s_i$ 表示第i条路线的路线长度。

$\underset{i\in S}{\min }{s}_i$ (3.15)

3.4. 支持增加传感器的SSC模型

基于SSC模型，本文以系统中传感器数量稳定为前提，得到了各传感器的MBC。为保证系统能够正常工作，在增加新传感器后，充电路径长度会增加，进而导致下一周期中MC的移动时间增加，因此在移动速率不变的前提下，可以通过减少间隔时间 $t_0$，使系统能够正常工作。在上文中，已知SSC模型为PDC模型迭代后的一般化模型，随着加入新传感器后周期数的增加，新系统最终也能达到稳定系统的状态，因此在原传感器电池容量不变的情况下，可以利用SSC模型对新加入传感器的MBC进行求解。

新问题可表述为：在原有系统基础上，新增m个传感器，记作 $S_{n+1},\cdots ,S_{n+m}$。加入新传感器后，最优路径会发生变化，新路径长度增加，每个周期MC在系统中的移动时间变为 ${T^{\prime }}_1$，充电完成后的间隔时间变为 ${t^{\prime }}_0$，全部耗电速率的数值和记为 ${C^{\prime }}_z$ ：

${C^{\prime }}_z={\displaystyle \underset{j=1}{\overset{n+m}{\sum }}{C}_j}.$ (3.16)

在系统中原传感器的MBC $E_1,E_2,\cdots ,E_n$ 大小不变的前提下，利用上述公式，可求解新系统下各传感器的理论MBC：

${E^{\prime }}_i=\frac{C_i\left({t^{\prime }}_0+{T^{\prime }}_1\right)\left(r-C_i\right)}{r-{C^{\prime }}_z}+f,i=1,\cdots ,n,n+1,\cdots ,n+m\text{.}$ (3.17)

为保证原系统中n个传感器能够正常工作，需要满足：

${E^{\prime }}_i\le E_i,i=1,\cdots ,n.$ (3.18)

化简，得：

${t^{\prime }}_0\le \min \left\{t_{temp}=\frac{\left(E_i-f\right)\left(r-{C^{\prime }}_z\right)}{C_i\left(r-C_i\right)}-{T^{\prime }}_1\right\},i=1,\cdots ,n.$ (3.19)

定理3.2在支持新增加传感器的WRSN中，(3.19)式中的 $t_{temp}$ 在系统充电循环内为定值，即与 $E_i$ 和 $C_i$ 无关。

证将(3.12)式中的 $E_i$ 代入到(3.19)式，计算可得：

${t^{\prime }}_0\le \frac{\left(t_0+T_1\right)\left(r-{C^{\prime }}_Z\right)}{r-C_Z}-{T^{\prime }}_1,i=1,\cdots ,n.$ (3.20)

即上限值与原先单个传感器的 $E_i$ 与 $C_i$ 无关，新系统的间隔时间仅与加入的新传感器有关。

此时，间隔时间的改变量：

$\Delta t_0=t_0-{t^{\prime }}_0.$ (3.21)

因此，添加新传感器的位置和自身的能量消耗速率后可得到新的WRSN系统相较于原先系统的间隔时间改变量 $\Delta t_0$，将满足(3.19)式的 ${t^{\prime }}_0$ 代入到(3.17)式中计算出每个新加入传感器的MBC，这样我们就给出了支持增加传感器的SSC模型的计算公式。

3.5. 支持增加传感器的多MC模型

本节将单MC下支持增加传感器的SSC模型进行推广，由基于MBC-GA-MTSP的多MC路线规划模型得到的每个MC的最优充电路线，以原系统各传感器所属子回路和实际最小MBC不变为前提，考虑新加入传感器的多MC充电路径规划问题。

问题可表述为：设原系统有M个充电器和n个传感器 $S_i\left(i=1,2,\cdots ,n\right)$，利用MBC-GA-MTSP规划出的最优路线中M条子路线分别记作 $R_i\left(i=1,2,\cdots ,n\right)$。在此基础上，该稳定系统新增m个传感器，记作 $S_j\left(j=n+1,n+2,\cdots ,n+m\right)$。已知新传感器的位置(经纬度)和能量消耗速率，利用(3.12)式可计算原MC稳定系统下每个传感器的理论MBC，而利用(3.17)式和(3.21)式即可求出改变的间隔时间和新传感器的MBC。

为了便于说明，定义 $d_{ij}\left(i=1,\cdots ,n;j=n+1,\cdots ,n+m\right)$ 为原传感器 $S_i$ 和新传感器 $S_j$ 之间的距离，可得出与每个新传感器最近的原传感器标号：

$y_j=\left\{i|{\min }_{1\le i\le n}{d}_{ij}\right\},j=n+1,\cdots ,n+m.$ (3.22)

对于每个新传感器 $S_j\left(j=n+1,\cdots ,n+m\right)$，将与其对应的 $S_{y_j}$ 所属子路线 $R_k\left(k=1,\cdots ,M\right)$ 作为新传感器的所属路径，最终确定每条子路线新增的传感器。基于以上分析，将每一个条子路线相关数据代入(3.17)和(3.21)式中即可算出对应子路线的充电器间隔时间及新加入传感器的MBC。

4. 数据实证

4.1. 数据的描述与分析

本文将网址 [17] 提供的数据代入上述模型中进行数据实证。以原生代(青岛)科技有限公司开发的海陆两用OE-ODO型光学氧气传感器的相关工作参数为参考，设定各参数值如下：

(i) 移动充电器的移动速度 $v=5\text{m}/\text{s}$。

(ii) 移动充电器的充电速率 $r=400\text{mA}/\text{h}$。

(iii) 传感器电量的最小阈值 $f=7.3\text{mA}$。

由节点经纬度测算任意两节点A，B间的实际距离，根据该距离数据构建权矩阵，可利用“改良圈–遗传算法”获得本实例的一条最短路，具体的路线如图3所示，求解得到最优路径值为11.4850 km。

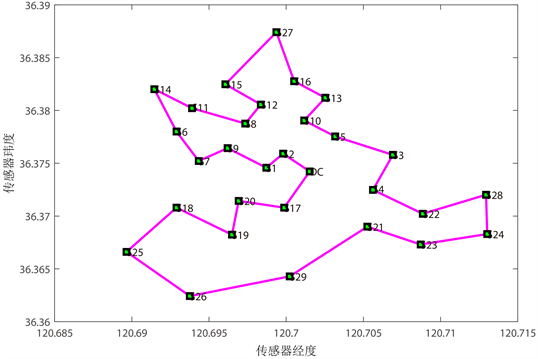
Figure 3. Charging roadmap by “improved circle + genetic algorithm”

图3. “改良圈–遗传算法”充电路线图

4.2. PDC模型和SSC模型的MBC求解

将参数值代入SSC模型的(3.12)式即可得到各传感器的MBC，同时，为了说明节点电池容量在周期跨度上的收敛性，下面也运用MATLAB分别计算了给定参数PDC模型的前10个周期的电池容量以及SSC模型下的电池容量，得到结果如表1所示。

Table 1. Comparison of solution values between PDC model and SSC model

表1. PDC模型与SSC模型求解值对比

可知，PDC模型推导的传感器MBC从第5周期开始就收敛于定值，且在给定相同参数值的情况下该值与SSC模型下传感器最小电容的求解值是一致的，则验证了SSC模型，能够较充分地说明PDC模型和SSC模型的可靠性和有效性。

4.3. MBC-GA-MTSP的多MC的路线规划求解

以派出4个移动充电器为例，利用MBC-GA-MTSP模型求解最优充电路线，此时 $k=7$，即派出的MC至少通过的传感器个数在区间[1, 7]范围内，这几种取值下的最短路线求解如图4和表2所示。

Figure 4. Path assignment graph under different minimum number of sensors

图4. 经过传感器最小个数不同情况下的路径分配图

Table 2. The shortest path with different minimum number of sensors

表2. 经过传感器最小个数不同情况下的最短路径

可以发现，虽然当MC至少经过1个传感器时的总路径最短，但此时路线分布不均匀，其中2个MC都仅通过1个传感器。得到全部路线后，我们将每种情况下的子路径节点信息代入(3.12)式计算MBC，取最大值后得到的结果如表3所示。

Table 3. Minimum and maximum battery capacity under different conditions

表3. 不同情况下的最小电池容量最大值

因此，可以得到 $S=\left\{3,4,6,7\right\}$，这些路线中， $i=3,4$ 对应的总路线长度最短，最短总路线长度为13.4845 km。所对应的4个MC的最优充电路线具体为：

※第一段： $DC\to S_2\to S_8\to S_{12}\to S_{10}\to DC$

※第二段： $DC\to S_1\to S_9\to S_7\to S_6\to S_{11}\to S_{14}\to S_{15}\to S_{27}\to S_{16}\to S_{13}\to S_5\to DC$

※第三段： $DC\to S_{17}\to S_{19}\to S_{29}\to S_{26}\to S_{25}\to S_{18}\to S_{20}\to DC$

※第四段： $DC\to S_3\to S_{28}\to S_{24}\to S_{23}\to S_{22}\to S_{21}\to S_4\to DC$

此时，每个传感器的最小电池容量也已经由(3.12)式求出。

4.4. 支持增加传感器的模型求解

假设原系统充电完成后的周期间隔 $t_0=300\text{s}$，代入到(3.12)式求解每个传感器的MBC值如表4所示。如在原传感器数据的基础上，新增1个传感器，节点编号记为30，已知传感器的经纬度及能量消耗速率分别为120.70˚，36.37˚，5.2 mA/h。利用“改良圈–遗传算法”求得新系统的最优路径值为11.6095 km，此时 ${T^{\prime }}_1=2321.9\text{s}$，代入到(3.20)式中可以算出 ${t^{\prime }}_0\le 220.7126\text{s}$。

Table 4. Relevant calculation when adding sensors

表4. 增加传感器的相关计算

最后，将计算出的结果代入到(3.21)式可以得出增加该传感器后系统间隔时间的改变量 $\Delta t_0\ge 79.2874\text{s}$，代入(3.17)式可得新增加的传感器MBC。对于支持增加传感器的多MC模型，利用类似的方法代入到相关公式即可求解。

4.5. 参数的灵敏度分析

在给定参数的情况下，能够通过SSC模型计算解析解直接求取对应的各节点MBC。由于现实中参数的设定存在一定不确定性，为使模型更具普适性，可选取不确定性较大的MC移动速度v和充电速率r两个参数进行灵敏度分析，以反映参数变化对模型解析所带来的影响。

设定 $v\in \left[1,10\right],r\in \left[200,1000\right]$，使用MATLAB软件做参数变动下MBC的变化示意图，如图5所示。

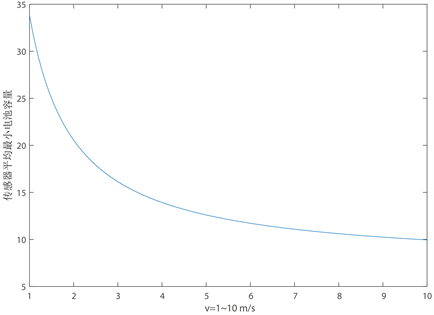
Figure 5. Sensitivity analysis of moving velocity and charging rate

图5. 移动速度和充电速率的灵敏度分析

基于上述参数的区间设定，分析上图可以发现，MC的移动速度以及其充电速率都与传感器的MBC呈现负相关关系，在距离起始点较近的有限区间里，两个参数的变动都对MBC产生了较为显著的影响，参数基数较大时的变动影响较小。

传感器的最低工作电量阈值f也会在一定程度上影响传感器的MBC，但是最低工作电量是传感器自身工作属性，与选择的传感器有关，非系统调控参数。总的来说，通过增加移动速度v以及提高充电速率r，可以达到降低传感器的MBC的目的。

5. 讨论、总结和展望

综上研究，本文从一个充电器的无线可充电传感器网络到多个充电器的无线可充电传感器网络均给出了最优路线和传感器最小电容量的求解方法，并根据实例进行了求解验证。在运用中，对于类似的无线可充电传感器网络，本方法都是适用的。

在单个充电器最小电池容量问题模型求解中，本文将数值解与解析解相结合，既解决了实际生产活动中路线规划问题，也便于对模型进行推广。本文还考虑了更一般化的场景，即在保持原有WRSN组件分布和系统参数不变的基础上，根据实际需要加入若干传感器，得到了改进的求解模型，使得充电方案规划更加灵活。在多个传感器充电问题中，本文考虑了基于最小电容量和最短移动路径及路线均衡性的最优充电路线方案，方案的适用性较好。

在后续的研究中，可以考虑传感器数量较多时针对现有算法进行优化，使其在较大网络中仍有较高的求解速度，也可以根据实际情况对均衡度进行新的定义，或者引入新的目标需求改进模型。

NOTES

^*通讯作者。