1. 引言
股票市场是金融体系中最为重要子市场,它反映了一国经济的“晴雨表” [1]。股票价格波动受到多种因素影响,其价格波动的产生、形成以及演化是一个典型的复杂系统 [2] [3] [4]。股票价格的剧烈波动会导致与其关联股票发生相应的波动,从而引发多米诺效应 [5]。最为典型的例子是2008年美国雷曼兄弟倒闭所引发的全球金融危机。因此,如何对股票市场中的重要股票进行识别就成为了一个热门的话题 [6]。
自Mantegna在1999年开创性将复杂网络理论运用于股票市场以来,运用复杂网络理论对股票市场中重要节点识别就成为了一个前沿的工具 [7]。Kenett等(2010) [8] 利用偏相关系数法构建了股票网络并运用出强度对网络中的重要节点进行识别,研究发现金融行业的股票是影响系统相关性的最有影响力的股票。谢赤等(2017) [9] 利用皮尔逊相关系数构建了股票网络并运用度对网络中的重要节点进行识别,研究发现制造业不管是在牛市还是在熊市都处于网络的中心地位。Wen等(2019) [10] 运用Copula模型构建了股票网络并运用点权对网络中重要节点进行识别,研究发现法国、英国等股票市场是网络中的重要节点。Huang等(2020a) [11] 运用滚动窗口皮尔逊相关系数构建了股票网络并运用出度、特征向量中心性等指标对网络中重要节点进行测度,研究发现新华制药、华泰股份以及航民股份是网络中的重要节点。Huang等(2020b) [12] 运用格兰杰(Granger)因果检验对中国股票市场构建了网络并运用Leaderrank值对网络中重要节点进行测度,研究发现制造业在网络中扮演了重要角色。
以上文献在构建股票网络时大多采用日度的低频数据 [7] - [12]。日度低频数据不能很好刻画股票日内波动信息。越来越多的学者认识到,频率为小时、分钟甚至更短的高频数据包含了丰富的资产价格信息,在金融风险管理中得到了广泛的研究 [13] [14] [15]。相比较于连续波动,跳跃波动能更好刻画股票市场剧烈波动 [16]。之所以选择格兰杰因果检验构建跳跃波动溢出网络,是因为格兰杰因果检验不仅能很好刻画单个股票之间联动的横截面和时变模式,而且能更直接描述市场之间波动溢出关系 [17]。本文拟通过选取2006年至2018年5分钟高频数据提取跳跃波动,并运用格兰杰因果检验构建跳跃波动溢出网络;然后,基于五种网络中心性(度中心性、接近度中心性、介数中心性、PageRank值和特征向量中心性)运用主成分分析法构建综合的网络中心性度量指标对网络中重要节点进行测度;最后,运用面板数据模型对影响网络节点的因素进行分析。
本文的创新点在于:1) 以往研究大多运用日度低频数据构建股票网络,本文通过选择5分钟高频数据构建了跳跃波动溢出网络。2) 本文在对股票网络中重要节点进行测度时运用了五种中心性测度方法,并通过主成分分析法构建了复合指标。
2. 研究方法
2.1. 跳跃波动网络的构建
2.1.1. 跳跃波动的提取
本文选取中国个股5分钟高频股价数据,并假定其对数价格服从标准的跳跃离散过程 [18]。股票对数收益的波动率可以通过二次变差来表示,它包含了跳跃波动和连续波动的无偏估计 [19]:
(1)
其中,等式右边前项表示连续波动过程;后项表示跳跃过程。
由于二次变差无法直接观察得到,本文用已实现波动率近似替代 [19]:
(2)
其中,
;Pi,t表示股票i在t时刻的收盘价;M = 48。
跳跃波动的提取可以用以下统计量进行识别 [20]:
(3)
其中,
(其中,
;
,
,
是连续波动
的估计值,通过非参数方法得到);
(其中,
)。
根据
与标准正态分布的统计量
进行比较,如果
,跳跃波动可以表示为 [19]:
(4)
其中,
为示性函数;
通常选择为0.05。
2.1.2. 基于格兰杰因果检验的跳跃波动网络的构建
在上一小节提取股票的跳跃波动之后,本小节采用基于VAR模型的格兰杰因果检验股票yt的跳跃波动是否对xt有显著的跳跃波动溢出关系。格兰杰因果检验模型表达如下 [21]:
(5)
其中,
为待估系数,
为残差项。通过计算两两股票市场之间的波动溢出关系,可以得到股票网络的邻接矩阵:
(6)
其中,V是网络的节点,E是网络边的集合,n表示网络节点个数,以及ADij表示如果Vi的跳跃波动是Vj的格兰杰因果原因,那么ADij等于1,否则等于0。
2.2. 网络节点中心性度量方法
2.2.1. 度中心性
节点的出度是指与节点i相连并指向其他节点的边数。出度反映了风险直接传递给与其连接的其他节点的情况。节点的出度越大,在风险蔓延过程中对其它节点影响就会越大。因此,度中心性定义为 [22]:
(7)
2.2.2. 介数中心性
两个不直接连接的股票之间的跳跃波动溢出取决于它们连接路径上的其他股票。当一支股票被其他许多股票之间的最短路径经过,则表示该股票在市场中很重要 [22]。其重要性或影响力可用网络节点的介数B来表征,定义为:
(8)
通过节点V最大可能的最短路径数为
,故节点V的介数中心性BC可以定义为:
(9)
2.2.3. 接近度中心性
度中心性虽然能反映一支股票直接波动溢出效应,而不是对其他所有股票的间接溢出效应。一支股票可能会直接影响到很多其他股票,但这些股票可能会与整个股票市场脱节,形成局部的社团。而接近度中心性(CC)可以衡量一个股票节点在整个股票网络中的中心程度。节点接近度中心性最自然的定义表示为 [22]:
(10)
即接近度中心性表示节点V到其他节点最短路径之和的倒数乘以其他节点个数。有向路径是一个连接其他节点的边序列,所有的边都指向同一个方向。
2.2.4. PageRank
PageRank (PR)算法 [1] 认为节点的重要性取决于与它相邻节点的重要性。假设网络中的每个节点获得一个相同的PR值,并将PR值平均的分配给它所指向的其他节点。经过多次迭代之后,各节点的PR值进入稳定的状态。PR值越大的节点越重要。公式如下:
(11)
2.2.5. 特征向量中心性
特征向量中心性 [1] 是节点重要性度量之一。它指派给网络中的每个节点一个相对得分,在对某个节点分值的贡献中,连接到高分值节点的连接比连接到低分值节点的连接大。对于节点V,它的特征向量中心性分值可以表示为:
(12)
其中,N为节点总数,
为最大的特征值。
2.2.6. 主成分分析
主成分分析(PCA)是一种数据降维技术 [22],通过对原始数据进行线性变换转换为一组线性无关的表示,用于提取数据的主要的具有代表性的分量指标。给定数据集
,其中
分别表示5种中心性度量值的列向量。首先对数据进行标准化之后计算协方差矩阵,以及协方差矩阵的特征值和相应的特征向量,我们假设特征值
降序排列,并设定阈值0.9,表示主成分贡献率计算目标维数k使方差百分比per满足:
。根据前k个特征值选择对应的k个特征向量
。通过加权相加得到综合度量值:
(13)
3. 实证分析
3.1. 数据来源、处理及基本统计描述
本文选择了2006年1月至2018年12月在中国A股上市的公司5分钟的收盘价数据。为了确保数据的可靠性,对数据进行如下处理 [23]:1) 删除在2006年1月之后上市的股票;2) 由于本文构建年度网络,因此对每年交易日数据缺失超过年总交易日20%的股票进行删除;3) 对少量缺失数据,使用前5分钟的数据进行替代。最终,我们获得了393支股票,数据来源于wind数据库。
高频数据抽样频率对股票波动率的抽样有显著的影响。抽样频率太低会导致测度跳跃波动不准确,抽样频率太高会产生微观噪音。因此,根据文献 [13] [14] [15],本文通过公式(1)~(4)计算股票的跳跃波动。各只股票跳跃波动的描述性统计分析如表1所示。
表1给出了393支股票跳跃波动值的描述性统计数据。研究发现跳跃波动序列的平均值和标准差变化范围从0.4508到3.7110以及从1.5024到12.0970。跳跃波动序列的峰度系数值远远大于0,这说明跳跃波动序列是右偏的。跳跃波动序列的峰度系数值远远大于3,这说明跳跃波动序列均是“尖峰厚尾”分布。此外,根据ADF-t值发现在1%的统计显着水平,跳跃波动是平稳的。因此,可用格兰杰因果检验对跳跃波动进行建模。

Table 1. Descriptive statistics of stock jump volatility
表1. 股票跳跃波动率的描述性统计
注:ADF检验的原假设为序列存在单位根。*,**,***分别表示在显著性水平为10%,5%,1%的情况下拒绝原假设。
3.2. 基于格兰杰因果检验的跳跃溢出网络的构建
为了构建跳跃波动溢出网络,本小节首先建立VAR模型,并选择最优的滞后阶数。然后,通过格兰杰因果检验股票i的跳跃波动对股票j的跳跃波动是否有显著的跳跃波动溢出。如果P值小于0.05,网络的边权信息保留,如果P值大于0.05,网络的边删除 [20]。最终,我们得到了13个有向股票网络。我们直接使用格兰杰因果网络的图来显示股票市场之间的跳跃波动溢出随时间的变化。图1和图2列出了在2011年和2015年市值排名前的100只股票网络。研究发现,在2015年中国“股灾”发生期间,股票市场之间的跳跃溢出效应是明显强于2011年的。
3.3. 网络节点重要性度量
中心性度量是为每个节点分配一个值,然后根据这个值的相对大小衡量节点的相对重要性。现在,我们分别从横截面和时间序列这两个维度来分析上述的五种中心性度量。图3从横截面的维度展示了2007年、2010年、2012年以及2014年样本期内平均市值最大的30支股票的五种中心性分值。为了直观的对不同中心性度量值之间进行比较,我们已将中心性分值进行归一化。从图中可以看出,在同一个网路中,不同节点的中心性分值是完全不同的。它表明,每个中心性分值都可以很好的区分股票之间的差异。例如,在2007年的网络中,第12个节点的PageRank最大,第11个节点的PageRank值最小。在同一个网络中,中心性度量的变化趋势是相似的,每个中心性度量值彼此之间正相关。例如,在2007年的网络中,度中心性度量值和PageRank值之间的Pearson相关系数为0.73。

Figure 1. The top 100 stock networks by market capitalization in 2011
图1. 基于市值排名前100的2011年股票网络

Figure 2. The top 100 stock networks by market capitalization in 2015
图2. 基于市值排名前100的2015年股票网络
图4从时间序列的维度显示了整个样本期内平均市值最大的四只股票(招商银行、上港集团、民生银行和中信证券)在样本期内的五种中心性分值。如图4所示股票的中心性测度在不同时期是动态变化的。随着时间的变化,同一股票的每个中心性度量值也将发生变化。我们以招商银行为例。其接近度中心性值在2013年上半年达到峰值,而最小值在2010年下半年出现。因此,某个节点在不同时间扮演的角色彼此之间存在很大差异。对于同一只股票,不同的中心性测度序列的变化趋势在大部分时期具有一定的相似性。我们以民生银行为例,两个网络中心性测度序列之间平均Pearson相关系数为0.62,且在1%水平下均显著。这表明中心性测度之间存在一定的正相关关系。意味着我们可以建立一个综合的中心性指数来评估网络中股票的中心性。
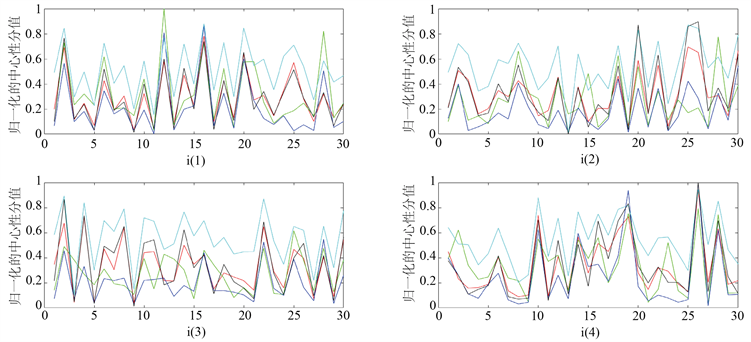
Figure 3. Centrality score in the dimensions of the cross section
图3. 横截面的维度下的中心性分值
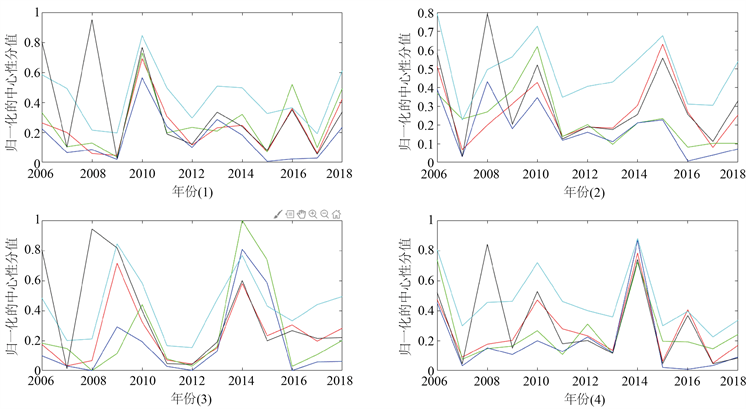
Figure 4. Centrality score under the dimension of time series
图4. 时间序列的维度下的中心性分值
接下来,我们运用主成分分析来对跳跃波动溢出网络的节点重要性进行综合度量。如前所述,在我们的分析中,我们考虑了393支股票和13个跳跃波动溢出网络。我们分别计算了13个网络节点的中心性综合度量值,并进行了排名。表2展示了在13个网络中至少3次排名在前39 (10%)名的17支股票。研究发现:1) 福星股份(SZ.000926)、上海机电(SH.600835)、长春高新(SZ.000661)是整个样本期间股票网络中的重要节点。其中,长春高新被投资者称为“百元股”,在样本期内价格上涨了5600%。2) 所展示的17支股票中,70.59%的股票市值超过了样本公司市值的中位数(6,066,199,821.78元)。这说明有影响力的股票公司通常都是大市值公司,并且在股票市场中占据了主导地位,体现了“大而不能倒”的理念。对于金融监管机构来说,应该对大市值公司予以重点关注。另一方面,也有少量的股票并不具有较大的市值,却也在跳跃波动溢出网络中起着重要作用,这也说明我们也需要关注“太关联而不能倒”。
为了保证上述结果(2)的稳健性,我们分别计算了在13个年度网络中心性综合度量值排名在前39 (10%)的股票市值,发现13年中平均每年约有26家(占39家的66.66%)大市值股票,同样意味着有影响力的股票公司通常都是大市值公司,说明我们的结果是稳健的。

Table 2. Important stocks identified by comprehensive metrics
表2. 综合度量识别的重要股票
注:第4列和第5列为股票在整个样本研究时期第一个交易日和最后一个交易日的股票收盘价。
3.4. 基于面板数据回归模型的网络节点重要性影响因素分析
如前所述,股票网络的中心性综合评估可用于衡量股票网络的节点中心性及其排名,从而分析单个股票在整个股票网络中的系统重要性。本部分旨在利用面板回归确定影响基于跳跃波动溢出网络节点重要性因素。通过借鉴Bu等(2019) [17] 和Huang和Wang (2018) [22] 的研究,选取了市值,资产收益率、负债率、换手率、市盈率、资产增长率、账面市值比这7个指标 [17]。
首先我们对变量进行平稳性检验,采用费雪式检验。表3显示了检验结果。结果强烈拒绝了面板单位根的原假设,因此,它们都是平稳的,可以作为面板数据回归模型的解释变量。我们将股票网络的中心性综合度量值作为因变量。然后我们在混合模型,固定效应模型,随机效应模型中进行选择,分别进行了F检验和LM检验,结果表4所示。在0.05的显著性水平上,拒绝F检验的原假设,接受了LM检验的原假设,故我们选择固定效应模型。面板数据回归模型的设定如式(14)。

Table 3. Test results of stationarity of panel data for each variable
表3. 各变量面板数据平稳性检验结果

Table 4. Fixed effect and random effect test
表4. 固定效应与随机效应的检验
(14)
表5是面板回归模型的估计结果。市值、市盈率、账面市值比和换手率分别在1%、5%和10%的显著性水平上具有正向影响。换手率在5%的显著性水平上具有负向影响。也就是说,具有较大的市值,市盈率,账面市值比和跳跃波动率,较小的换手率的股票在整个股票网络中具有比较重要的地位。尽管资产收益率,负债率和资产增长率的变量系数并不显著,但是模型的F检验在1%的显著性水平上是显著的。这表明数据是适合模型的。因此,在对股票市场中比较重要的股票进行监管时,可以从市场和公司会计方面的诸如市值,市盈率,账面市值比,跳跃波动率和换手率进行分析。

Table 5. The results of panel data regression
表5. 面板回归结果
4. 结论
本文通过选取中国A股股票日内5分钟高频股价数据提取各股票的跳跃波动,并采用格兰杰因果检验构建跳跃波动溢出网络。进一步地,提出主成分分析方法对五种网络中心性度量方法进行主成分方法构建测度网络中重要节点复合指标。最后,考察市值、资产收益率、负债率、换手率、市盈率、资产增长率和账面市值比这七个指标对网络中节点重要性的影响程度。本文主要结论如下:1) 福星股份(SZ.000926)、上海机电(SH.600835)、长春高新(SZ.000661)等在大部分时期是股票网络中的重要节点。2) 70%的重要节点具有较大市值,与“大而不能倒”的观点相吻合。此外,市值较小的节点在跳跃波动溢出网络中也扮演着重要角色,这也意味着不能忽视“太关联而不能倒”。3) 具有较大市值、市盈率、账面市值比以及较小换手率的股票,在跳跃波动溢出网络中占据重要的地位。
本文的政策建议如下:1) 有影响力的公司通常具有较大市值或者较强的系统关联性。监管机构部门必须更多地关注大市值公司以及在市场中具有较强关联性的公司,防范金融市场“太大而不倒”风险的同时也要关注“太关联而不倒”的风险。2) 在对股票市场中比较重要的股票进行监管时,可以从市场和公司会计方面的诸如市值、市盈率、账面市值比和换手率进行分析。监管者不但要关注股票市场因素,而且要关注上市公司财务层面的变化,来提高股票市场稳定性,确保守住不发生系统性金融风险的底线。
基金项目
湖南省自然科学基金面上项目(2019JJ40307);湖南省教育厅优秀青年基金(18B155);湖南省教育厅项目(18C0220);长沙理工大学国际合作拓展项目(2019IC38)。
NOTES
*通讯作者。