多元线性回归的中心化和标准化实验结果比较

Comparison of Centralized and Standardized Experimental Results of Multiple Linear Regression

摘要: 在讨论一元线性回归模型的时候，我们可以看出，对数据进行中心化处理后，推导计算过程会简化许多。由此想到，对于多元线性回归模型，能否也对数据进行中心化处理，或者进一步的标准化处理，以期简化计算？实际上，经过中心化和标准化处理，可得到均值为0，标准差为1的数据，从而在进行多元线性回归拟合时消除了因量纲不同或数值差异较大而引起的误差。

Abstract: When discussing the unary linear regression model, we can see that the derivation and calculation process will be much simplified after centralized data processing. Therefore, for the multiple linear regression model, can the data also be processed centrally or further standardized to simplify the calculation? In fact, data with a mean value of 0 and a standard deviation of 1 can be obtained after centralized and standardized processing, so that errors caused by different dimensions or large numerical differences can be eliminated when performing multiple linear regression fitting.

1. 实验方法与步骤

首先在一元线性模型的基础上，推导多元线性模型相关系数的求解公式；之后利用产生的随机数分别按不做处理、做中心化处理、做标准化处理计算相应的未知参数；最后通过比较计算得到的未知参数，分析中心化和标准化处理的好处。

2. 实验过程

2.1. 公式推导

2.1.1. 一元线性回归未中心 [1]

对 $y={\beta }_0+{\beta }_1{x}_1+\epsilon$

$\{\begin{array}{l}{y}_1={\beta }_0+{\beta }_1{x}_1+{\epsilon }_1\\ ⋮\\ y_n={\beta }_0+{\beta }_1{x}_n+{\epsilon }_n\end{array}$

记 $y=\left(\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right),X=\left(\begin{array}{cc}1& x_1\\ ⋮& ⋮\\ 1& x_n\end{array}\right),\epsilon =\left(\begin{array}{c}{\epsilon }_1\\ ⋮\\ {\epsilon }_n\end{array}\right)$，

则有 $L=X^{\prime }X=\left(\begin{array}{cc}n& n\bar{x}\\ n\bar{x}& {\displaystyle {\sum }_{t=1}^n{x}_t^2}\end{array}\right)$。

$L^{-1}=\frac{1}{n{\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2}}\left(\begin{array}{cc}{\displaystyle {\sum }_{t=1}^n{x}_t^2}& n\bar{x}\\ -n\bar{x}& n\end{array}\right)$

其中， $\bar{x}=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{x}_t}$， $\bar{y}=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{y}_t}$。

$\hat{\beta }=L^{-1}{X}^{\prime }y=\frac{1}{n{\displaystyle {\sum }_{t=1}^n{\left(x_t-x\right)}^2}}\left(\begin{array}{c}n\bar{y}{\displaystyle {\sum }_{t=1}^n{x}_t^2}-n\bar{x}{\displaystyle {\sum }_{t=1}^n{x}_t{y}_t}\\ n{\displaystyle {\sum }_{t=1}^n{x}_t{y}_t}-n^2\bar{x}\bar{y}\end{array}\right)$

${\sigma }^2=\frac{1}{n}{\left(y-X\hat{\beta }\right)}^{\prime }\left(y-X\hat{\beta }\right)=s_2^2-{\hat{\beta }}_1^2{s}_1^2$

其中 $s_1^2=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2},s_2^2=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(y_t-\bar{y}\right)}^2}$。

则 $\hat{y}={\hat{\beta }}_0+{\hat{\beta }}_{1}x$。

2.1.2. 一元线性回归的中心化

对 $y={\beta }_0+{\beta }_1\left(x-\bar{x}\right)+\epsilon$

即 $\{\begin{array}{l}{y}_1={\beta }_0+{\beta }_1\left(x-\bar{x}\right)+{\epsilon }_1\\ ⋮\\ y_n={\beta }_0+{\beta }_1\left(x_n-\bar{x}\right)+{\epsilon }_n\end{array}$

其中 $\bar{x}=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{x}_t}$。

对数据 $x_1,x_2,\cdots ,x_n$ 作中心化处理，利用新的n组数据 $\left(y_t,x_t-x\right)$， $t=1,2,\cdots ,n$。

建立线性回归方程 $\hat{y}={\hat{\beta }}_0+{\hat{\beta }}_1\left(x-\bar{x}\right)$。

记 $y=\left(\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right),X=\left(\begin{array}{cc}1& x_1-\bar{x}\\ ⋮& ⋮\\ 1& x_n-\bar{x}\end{array}\right)$

$L=X^{\prime }X=\left(\begin{array}{cc}n& 0\\ 0& {\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2}\end{array}\right)$

$L^{-1}=\frac{1}{n{\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2}}\left(\begin{array}{cc}{\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2}& 0\\ 0& n\end{array}\right)$

记 $s_1^2=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2},s_2^2=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(y_t-\bar{y}\right)}^2}$

$\hat{\beta }=L^{-1}{X}^{\prime }y=\frac{1}{n{\displaystyle {\sum }_{t=1}^n{\left(x_t-x\right)}^2}}\left(\begin{array}{c}n\bar{y}{\displaystyle {\sum }_{t=1}^n{\left(x_t-\bar{x}\right)}^2}\\ n{\displaystyle {\sum }_{t=1}^n\left(x_t-\bar{x}\right)y_t}\end{array}\right)=\frac{1}{n{s}_1^2}\left(\begin{array}{c}n{s}_1^{2}y\\ n{s}_{12}\end{array}\right)$

${\sigma }^2=\frac{1}{n}{\left(y-X\hat{\beta }\right)}^{\prime }\left(y-X\hat{\beta }\right)=s_2^2-{\hat{\beta }}_1^2{s}_1^2$

记 $R=\frac{s_{12}}{s_1\cdot s_2}$，

则有 ${\hat{\beta }}_1=\frac{s_{12}}{s_1^2}=R\frac{s_2}{s_1}$。

${\hat{\sigma }}^2=s_2^2-{\left(R\frac{s_2}{s_1}\right)}^2{s}_1^2=\left(1-R^2\right)s_2^2$

2.1.3. 多元线性回归的中心化

样本数据的中心化公式：

${\stackrel{\dot{}}{x}}_{it}=x_{it}-{\bar{x}}_i\left(i=1,2,\cdots ,k;t=1,2,\cdots ,n\right),{\stackrel{\dot{}}{y}}_t=y_t-\bar{y}\left(t=1,2,\cdots ,n\right)$

其中： ${\bar{x}}_i=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{x}_{it}},\bar{y}=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{y}_t}$

$\therefore \stackrel{\dot{}}{Y}=\stackrel{\dot{}}{X}B+e$

其中

$\stackrel{\dot{}}{Y}=\left(\begin{array}{c}\begin{array}{c}{\stackrel{\dot{}}{y}}_1\\ {\stackrel{\dot{}}{y}}_2\end{array}\\ \begin{array}{c}⋮\\ {\stackrel{\dot{}}{y}}_n\end{array}\end{array}\right),\stackrel{\dot{}}{X}=\left(\begin{array}{cc}\begin{array}{cc}{\stackrel{\dot{}}{x}}_{11}& {\stackrel{\dot{}}{x}}_{21}\\ {\stackrel{\dot{}}{x}}_{12}& {\stackrel{\dot{}}{x}}_{22}\end{array}& \begin{array}{cc}\cdots & {\stackrel{\dot{}}{x}}_{k1}\\ \cdots & {\stackrel{\dot{}}{x}}_{k2}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ {\stackrel{\dot{}}{x}}_{1n}& {\stackrel{\dot{}}{x}}_{2n}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & {\stackrel{\dot{}}{x}}_{kn}\end{array}\end{array}\right),B=\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_k\end{array}\right),e=\left(\begin{array}{c}{e}_1\\ e_2\\ ⋮\\ e_n\end{array}\right)$

用最小二乘原理求出参数B的估计量 $\hat{B}$ ：

根据最小二乘原理，需寻找一组参数估计值 $\hat{B}$，使残差平方和 $e^{\prime }e={\left(\stackrel{\dot{}}{Y}-\stackrel{\dot{}}{X}\hat{B}\right)}^{\prime }\left(\stackrel{\dot{}}{Y}-\stackrel{\dot{}}{X}\hat{B}\right)={\stackrel{\dot{}}{Y}}^{\prime }\stackrel{\dot{}}{Y}-2{\stackrel{\dot{}}{Y}}^{\prime }\stackrel{\dot{}}{X}\hat{B}+{\hat{B}}^{\prime }{\stackrel{\dot{}}{X}}^{\prime }\stackrel{\dot{}}{X}\hat{B}$ 最小。

于是参数的最小二乘估计值为

$\hat{B}={\left({\stackrel{\dot{}}{X}}^{\text{'}}\stackrel{\dot{}}{X}\right)}^{-1}{\stackrel{\dot{}}{X}}^{\prime }\stackrel{\dot{}}{Y}$

中心化回归模型只包含k个参数估计值 ${\hat{b}}_1,{\hat{b}}_2,\cdots ,{\hat{b}}_k$。

对于(10)：

$\begin{array}{c}{\stackrel{\dot{}}{X}}^{\prime }\stackrel{\dot{}}{X}=\left(\begin{array}{cc}\begin{array}{cc}{\stackrel{\dot{}}{x}}_{11}& {\stackrel{\dot{}}{x}}_{12}\\ {\stackrel{\dot{}}{x}}_{21}& {\stackrel{\dot{}}{x}}_{22}\end{array}& \begin{array}{cc}\cdots & {\stackrel{\dot{}}{x}}_{1n}\\ \cdots & {\stackrel{\dot{}}{x}}_{2n}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ {\stackrel{\dot{}}{x}}_{k1}& {\stackrel{\dot{}}{x}}_{k2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & {\stackrel{\dot{}}{x}}_{kn}\end{array}\end{array}\right)\left(\begin{array}{cc}\begin{array}{cc}{\stackrel{\dot{}}{x}}_{11}& {\stackrel{\dot{}}{x}}_{21}\\ {\stackrel{\dot{}}{x}}_{12}& {\stackrel{\dot{}}{x}}_{22}\end{array}& \begin{array}{cc}\cdots & {\stackrel{\dot{}}{x}}_{k1}\\ \cdots & {\stackrel{\dot{}}{x}}_{k2}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ {\stackrel{\dot{}}{x}}_{1n}& {\stackrel{\dot{}}{x}}_{2n}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & {\stackrel{\dot{}}{x}}_{kn}\end{array}\end{array}\right)\\ =\left(\begin{array}{cccc}{\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{1t}}& {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{1t}{\stackrel{\dot{}}{x}}_{2t}}& \cdots & {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{1t}{\stackrel{\dot{}}{x}}_{kt}}\\ {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{2t}{\stackrel{\dot{}}{x}}_{1t}}& {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{2t}}& \cdots & {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{2t}{\stackrel{\dot{}}{x}}_{kt}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{kt}{\stackrel{\dot{}}{x}}_{1t}}& {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{kt}{\stackrel{\dot{}}{x}}_{2t}}& \cdots & {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{kt}}\end{array}\right)\end{array}$

${\stackrel{\dot{}}{X}}^{\prime }\stackrel{\dot{}}{Y}=\left(\begin{array}{cc}\begin{array}{cc}{\stackrel{\dot{}}{x}}_{11}& {\stackrel{\dot{}}{x}}_{12}\\ {\stackrel{\dot{}}{x}}_{21}& {\stackrel{\dot{}}{x}}_{22}\end{array}& \begin{array}{cc}\cdots & {\stackrel{\dot{}}{x}}_{1n}\\ \cdots & {\stackrel{\dot{}}{x}}_{2n}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ {\stackrel{\dot{}}{x}}_{k1}& {\stackrel{\dot{}}{x}}_{k2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & {\stackrel{\dot{}}{x}}_{kn}\end{array}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}{\stackrel{\dot{}}{y}}_1\\ {\stackrel{\dot{}}{y}}_2\end{array}\\ \begin{array}{c}⋮\\ {\stackrel{\dot{}}{y}}_n\end{array}\end{array}\right)=\left(\begin{array}{c}\begin{array}{c}{\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{1t}{\stackrel{\dot{}}{y}}_t}\\ {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{2t}{\stackrel{\dot{}}{y}}_t}\end{array}\\ \begin{array}{c}⋮\\ {\displaystyle {\sum }_{t=1}^n{\stackrel{\dot{}}{x}}_{kt}{\stackrel{\dot{}}{y}}_t}\end{array}\end{array}\right)$

2.1.4. 多元线性回归的标准化

样本数据的标准化公式：

$x_{it}^{\ast }=\frac{x_{it}-{\bar{x}}_i}{\sqrt{{{\displaystyle \sum }}^{\text{}}{\left(x_{it}-{\bar{x}}_i\right)}^2/\left(n-1\right)}}=\frac{{\stackrel{\dot{}}{x}}_{it}}{\sqrt{{{\displaystyle \sum }}^{\text{}}{\stackrel{\dot{}}{x}}_{it}^2/\left(n-1\right)}}=\frac{{\stackrel{\dot{}}{x}}_{it}}{\sigma x_i}\left(i=1,2,\cdots ,k\right)$

$y_t^{\ast }=\frac{y_t-\bar{y}}{\sqrt{{{\displaystyle \sum }}^{\text{}}{\left(y_t-\bar{y}\right)}^2/\left(n-1\right)}}=\frac{{\stackrel{\dot{}}{y}}_t}{\sqrt{{{\displaystyle \sum }}^{\text{}}{\left(y_t-\bar{y}\right)}^2/\left(n-1\right)}}=\frac{{\stackrel{\dot{}}{y}}_t}{\sigma y}\left(t=1,2,\cdots ,n\right)$

同中心化类似，用最小二乘方法，求出标准化的样本数据 $\left({\tilde{y}}_t,{\tilde{x}}_{1t},{\tilde{x}}_{2t},\cdots ,{\tilde{x}}_{kt}\right)$ 的经验回归方程，记为 ${\hat{y}}_t^{\ast }={\hat{b}}_1^{\ast }{x}_{1t}^{\ast }+{\hat{b}}_2^{\ast }{x}_{2t}^{\ast }+\cdots +{\hat{b}}_k^{\ast }{x}_{kt}^{\ast }$。

其中： ${\hat{b}}_1^{\ast },{\hat{b}}_2^{\ast },\cdots ,{\hat{b}}_k^{\ast }$ 为y对自变量 $x_1,x_2,\cdots ,x_k$ 的标准化回归系数，标准化包括了中心化。

标准化回归系数与最小二乘回归系数之间存在关系式 ${\hat{b}}_i^{\ast }=\frac{\sigma x_i}{\sigma y}{\hat{b}}_i\left(i=1,2,\cdots ,k\right)$。

其中： $\sigma x_i,\sigma y$ 为 $x_i,y$ 的样本标准差，普通最小二乘估计 ${\hat{b}}_i$ (或中心化回归系数)表示在其他变量不变的情况下，自变量 $x_i$ 的每单位的绝对变化引起的因变量均值的绝对变化量。

标准化回归系数 ${\hat{b}}_t^{\ast }$ 表示自变量 $x_i$ 的1%相对变化(相对于标准差)引起的因变量均值的相对变化百分数(相对于标准差)。

由样本观测值 $x_{i1},x_{i2},\cdots ,x_{ik}\left(i=1,2,\cdots ,n\right)$，分别计算 $x_i$ 与 $x_j$ 的简单相关系数 $r_{ij}$，得自变量样本相关系

数矩阵 $R=\left(\begin{array}{cccc}1& r_{12}& \cdots & r_{1k}\\ r_{21}& 1& \cdots & r_{2k}\\ ⋮& ⋮& \ddots & ⋮\\ r_{k1}& r_{k2}& \cdots & 1\end{array}\right)$。

若记： $X^{\ast }={\left(x_{ij}^{\ast }\right)}_{n\times k}$，表示标准化的设计阵，则相关系数矩阵可以表示为

$R={\left(X^{\ast }\right)}^{\prime }{X}^{\ast }=\left(\begin{array}{cccc}1& r_{12}& \cdots & r_{1k}\\ r_{21}& 1& \cdots & r_{2k}\\ ⋮& ⋮& \ddots & ⋮\\ r_{k1}& r_{k2}& \cdots & 1\end{array}\right)$

相关系数矩阵R是对称矩阵，若 $X^{\ast }$ 满秩，则R为对称正定矩阵。

2.2. 实验数据运行

2.2.1. 一元线性模型 不做处理

matlab程序：

x_1=[143 144 145 147 148 150 153 154 155 156 157 158 159 160 161 162]';

X=[ones(16,1),x_1];

Y=[87 85 88 91 92 90 93 95 98 98 97 95 97 99 100 102]';

[b,bint,r,rint,stats]=regress(Y,X)

t=1:16;

figure(1);

y_fitting=X(t,:)*b;

plot(t,y_fitting,'r-',t,Y(t,:),'b-',t,abs(y_fitting-Y(t,:)),'k-');

legend('红--拟合值','蓝--实际值','黑--误差值');

text(8,50,strcat('相关系数R=',num2str(stats(1,1))));

text(8,40,strcat('F=',num2str(stats(1,2))));

text(8,30,strcat('P=',num2str(stats(1,3),'%f')));

nhfcsl=strcat('拟合方程式Y1=',num2str(b(1,1)),'+',num2str(b(2,1)),'*x1');

text(8,20,nhfcsl);

title('线性回归方程拟合结果');

xlabel('样本点');ylabel('y');

figure(2);

u1=rint(:,1);

I1=rint(:,2);

plot(t,I1,'b-',t,r,'R*',t,u1,'g-');

legend('蓝--残差95%置信区间的上限','红--残差值','绿--残差95%置信区间下限');

xlabel('样本点');ylabel('残差值');

运行结果如图1和图2：

stats = 0.9047132.8768 0.0000 2.5357

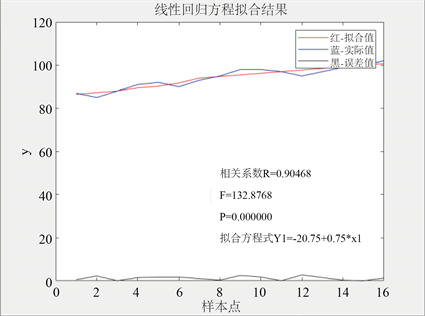
Figure 1. Fitting results of linear regression equation with one variable

图1. 一元线性回归方程拟合结果

Figure 2. Diagramof the sample residual

图2. 样本残差图

由以上运行结果可得到：

参数的估计： ${\hat{b}}_0=-20.7500,{\hat{b}}_1=0.7500$

$\therefore$ 回归方程为： $\hat{y}=-20.7500+0.7500x_1$ (1)

$b_0$ 的区间估计： $\left(-42.1526,0.6526\right)$

$b_1$ 的区间估计： $\left(0.6105,0.8895\right)$。

拟合优度(回归平方和和总离差平方和的比值) $R^2=0.9047$，表示回归值对观测值的拟合程度，值越接近1，说明回归直线对观测值的拟合程度越好。

F值(方差检验量) $F=132.8768$，是整个模型的整体检验，值越大，说明回归方程越显著。

p值 $p=0.000000$，其值小于0.05或0.01时说明系数通过检验。

结论：将残差的置信上下限和实际残差值绘制出来后可看到，残差值都在区间内，回归模型正常；将实际数据值和拟合值分别绘制成折线图之后可看到，两条曲线非常接近，可从直观上说明拟合程度较好。从数值上，拟合优度接近1，方差检验量也较大，p值也说明系数通过了检验。故上述回归方程拟合较好。

2.2.2. 一元线性模型 做中心化处理(减均值)

x_1=[143 144 145 147 148 150 153 154 155 156 157 158 159 160 161 162]';

a_1=mean(x_1')

X=[ones(16,1),x_1-a_1];

Y=[87 85 88 91 92 90 93 95 98 98 97 95 97 99 100 102]';

b_1=mean(Y')

Y=Y-b_1;

[b,bint,r,rint,stats]=regress(Y,X)

t=1:16;

类似地，可得到：

参数的估计： ${\hat{b}}_0=0.0000,{\hat{b}}_1=0.7500$

$\therefore$ 回归方程为： $\widehat{\stackrel{\dot{}}{y}}=0.7500{\stackrel{\dot{}}{x}}_1$

又 ${\bar{x}}_1=153.2500,\bar{y}=94.1875$

代回原始数据得： $\hat{y}-\bar{y}=0.7500\left(x_1-\bar{x}\right)$

即

$\hat{y}=-20.7500+0.7500x_1$ (2)

$b_0$ 的区间估计： $\left(-0.8538,0.8538\right)$

$b_1$ 的区间估计： $\left(0.6105,0.8895\right)$

拟合优度 $R^2=0.9047$ 方差检验量 $F=132.8768$ p值 $p=0.0000$。

2.2.3. 一元线性模型 做标准化处理(减均值再除以标准差)

x_1=[143 144 145 147 148 150 153 154 155 156 157 158 159 160 161 162]';

a_1=mean(x_1')

s_x=std(x_1)

X=[ones(16,1),(x_1-a_1)/s_x];

Y=[87 85 88 91 92 90 93 95 98 98 97 95 97 99 100 102]';

b_1=mean(Y')

s_y=std(Y')

Y=(Y-b_1)/s_y;

[b,bint,r,rint,stats]=regress(Y,X)

t=1:16;

参数的估计： ${\hat{b}}_0=0.0000,{\hat{b}}_1=0.9511$

$\therefore$ 回归方程为： $\widehat{\stackrel{\dot{}}{y}}=0.9511x_1^{*}$

又 ${\bar{x}}_1=153.2500,\bar{y}=94.1875,s_x=6.3193,s_y=4.9829$

代回原始数据得： $\frac{\hat{y}-\bar{y}}{s_y}=\frac{0.9511\left(x_1-\bar{x}\right)}{s_x}$

即

$\hat{y}=-20.7500+0.7500x_1$ (3)

$b_0$ 的区间估计： $\left(-0.1714,0.1714\right)$。

$b_1$ 的区间估计： $\left(0.7742,1.1281\right)$。

拟合优度 $R^2=0.9047$ 方差检验量 $F=132.8768$ p值 $p=0.0000$。

2.2.4. 多元线性模型 不做处理

matlab程序：

x_1=[143 144 145 147 148 150 153 154 155 156 157 158 159 160 161 162]';

x_2=unifrnd(2,4,16,1);

x_3=rand(16,1);

X=[ones(16,1),x_1,x_2,x_3*10];

Y=[87 85 88 91 92 90 93 95 98 98 97 95 97 99 100 102]';

[b,bint,r,rint,stats]=regress(Y,X)

t=1:16;

figure(1);

y_fitting=X(t,:)*b;

plot(t,y_fitting,'r-',t,Y(t,:),'b-',t,abs(y_fitting-Y(t,:)),'k-');

legend('红--拟合值','蓝--实际值','黑--误差值');

text(2,50,strcat('相关系数R=',num2str(stats(1,1))));

text(2,50,strcat('F=',num2str(stats(1,2))));

text(2,50,strcat('P=',num2str(stats(1,3),'%f')));

nhfcsl=strcat('拟合方程式Y1=',num2str(b(1,1)),'+',num2str(b(2,1)),'*x1','+',num2str(b(3,1)),'*x2','+', num2str(b(4,1)),'*x3');

text(2,50,nhfcsl);

title('线性回归方程拟合结果');

xlabel('样本点');ylabel('y');

figure(2);

u1=rint(:,1);

I1=rint(:,2);

plot(t,I1,'b-',t,r,'R*',t,u1,'g-');

legend('蓝--残差95%置信区间的上限','红--残差值','绿--残差95%置信区间下限');

xlabel('样本点');ylabel('残差值');

运行结果如图3：

stats = 0.9069 38.9804 0.0000 2.8884

Figure 3. Fitting results of multiple linear regression equations

图3. 多元线性回归方程拟合结果

由以上运行结果可得到：

参数的估计： ${\hat{b}}_0=-23.2385,{\hat{b}}_1=0.7629,{\hat{b}}_2=0.0390,{\hat{b}}_3=0.0781$

$\therefore \hat{y}=-23.3285+0.7629x_1+0.0390x_2+0.0781x_3$ (4)

$b_0$ 的区间估计： $\left(-48.7709,2.1139\right)$。

$b_1$ 的区间估计： $\left(0.6014,0.9244\right)$。

$b_2$ 的区间估计： $\left(-1.4414,1.5195\right)$。

$b_3$ 的区间估计： $\left(-0.2778,0.4340\right)$。

拟合优度(回归平方和和总离差平方和的比值) $R^2=0.9069$，表示回归值对观测值的拟合程度，值越接近1，说明回归直线对观测值的拟合程度越好。

F值(方差检验量) $F=38.9804$，是整个模型的整体检验，值越大，说明回归方程越显著。

p值 $p=0.000002$，其值小于0.05或0.01时说明系数通过检验。

结论：将残差的置信上下限和实际残差值绘制出来后可看到，残差值都在区间内，回归模型正常；将实际数据值和拟合值分别绘制成折线图之后可看到，两条曲线非常接近，可从直观上说明拟合程度较好。从数值上，拟合优度接近1，方差检验量也较大，p值也说明系数通过了检验。故上述回归方程拟合较好。

2.2.5. 多元线性模型 做中心化处理(减均值)

x_1=[143 144 145 147 148 150 153 154 155 156 157 158 159 160 161 162]';

x_2=unifrnd(2,4,16,1);

x_3=rand(16,1)*10;

a_1=mean(x_1')

a_2=mean(x_2')

a_3=mean(x_3')

X=[ones(16,1),x_1-a_1,x_2-a_2,x_3-a_3];

Y=[87 85 88 91 92 90 93 95 98 98 97 95 97 99 100 102]';

b_1=mean(Y')

Y=Y-b_1;

[b,bint,r,rint,stats]=regress(Y,X)

t=1:16;

类似地，可得到：

参数的估计： ${\hat{b}}_0=0.0000,{\hat{b}}_1=0.7629,{\hat{b}}_2=0.0390,{\hat{b}}_3=0.0781$

$\therefore \hat{y}=0.7629{\stackrel{\dot{}}{x}}_1+0.0390{\stackrel{\dot{}}{x}}_2+0.0781{\stackrel{\dot{}}{x}}_3$

又 ${\bar{x}}_1=153.2500,{\bar{x}}_2=3.2189,{\bar{x}}_3=6.0626,\bar{y}=94.1875$

代回原数据： $\hat{y}-\bar{y}=0.7629\left(x_1-{\bar{x}}_1\right)+0.0390\left(x_2-{\bar{x}}_2\right)+0.0781\left(x_3-{\bar{x}}_3\right)$

即

$\hat{y}=-23.3260+0.7629x_1+0.0390x_2+0.0781x_3$ (5)

$b_0$ 的区间估计： $\left(-0.9257,0.9257\right)$。

$b_1$ 的区间估计： $\left(0.6014,0.9244\right)$。

$b_2$ 的区间估计： $\left(-1.4414,1.5195\right)$。

$b_3$ 的区间估计： $\left(-0.2778,0.4340\right)$。

拟合优度 $R^2=0.9069$，方差检验量 $F=38.9804$，p值 $p=0.0000$。

2.2.6. 多元线性模型 做标准化处理(减均值再除以标准差)

x_1=[143 144 145 147 148 150 153 154 155 156 157 158 159 160 161 162]';

x_2=unifrnd(2,4,16,1);

x_3=rand(16,1)*10;

a_1=mean(x_1')

a_2=mean(x_2')

a_3=mean(x_3')

s_1=std(x_1)

s_2=std(x_2)

s_3=std(x_3)

X=[ones(16,1),(x_1-a_1)/s_1,(x_2-a_2)/s_2,(x_3-a_3)/s_3];

Y=[87 85 88 91 92 90 93 95 98 98 97 95 97 99 100 102]';

b_1=mean(Y')

s_y=std(Y)

Y=(Y-b_1)/s_y;

[b,bint,r,rint,stats]=regress(Y,X)

t=1:16;

参数的估计： ${\hat{b}}_0=0.0000,{\hat{b}}_1=0.9827,{\hat{b}}_2=-0.1857,{\hat{b}}_3=0.0260$

$\therefore \hat{y}=4.7335x_1^{*}-0.1463x_2^{*}+0.1246x_3^{*}$

又 ${\bar{x}}_1=153.2500,{\bar{x}}_2=2.8550,{\bar{x}}_3=5.1213,\bar{y}=94.1875$

$s_1=6.3193,s_2=0.4895,s_3=3.6571,s_y=4.9829$

代回原数据： $\frac{\hat{y}-\bar{y}}{s_y}=\frac{0.7629\left(x_1-{\bar{x}}_1\right)}{s_1}+\frac{0.0390\left(x_2-{\bar{x}}_2\right)}{s_2}+\frac{0.0781\left(x_3-{\bar{x}}_3\right)}{s_3}$

即

$\hat{y}=0.3140+0.6016x_1+0.3970x_2+0.1064x_3$ (6)

$b_0$ 的区间估计： $\left(-0.1580,0.1580\right)$。

$b_1$ 的区间估计： $\left(0.8137,1.1517\right)$。

$b_2$ 的区间估计： $\left(-0.4060,0.0345\right)$。

$b_3$ 的区间估计： $\left(-0.1916,0.2435\right)$。

拟合优度 $R^2=0.9327$ 方差检验量 $F=55.3995$ p值 $p=0.0000$。

3. 实验结论

对一元线性回归模型，由以上的数据模拟可看出，不做处理，做中心化处理和做标准化处理均没有改变 $R^2,F$ 的值；未代回原始数据之前，和不做处理相比，中心化处理后的线性回归方程少了常数项，相当于是做了坐标轴的平移，标准化处理后的线性回归方程不仅少了常数项，系数也发生了改变，相当于改变了坐标的分度值；但代回原始数据之后，三个线性方程相同。

对多元线性回归，可以看出，做了中心化处理之后，得到的方程不含常数项，其他系数和 $R^2,F$ 值均相同，且代回原始数据之后得到和不做处理相同的回归方程；做了标准化处理后，各系数的值均有不同程度的变化，由于有随机数的参与，此时无法准确比较，但观察数据，不做任何处理时计算出来的结果会由于值的大小，比如第一行数据和第二行数据相差近100倍，产生的相应的估计有较大的差距。但透过数据的变化情况，两个因素对响应变量的影响又很接近，这也就告诉我们，在比较影响时不能直接比较，需要做标准化处理。

总之，数据的中心化处理相当于将坐标轴的原点移至样本中心，数据的标准化处理相当于是将不同指标化为同一尺度标准和数量级，方便比较。

特别地，在用多元线性回归方程描述某种经济现象时，由于自变量所用的单位大都不同，数据的大小差异也往往很大，这就不利于放在同一标准上进行比较。将样本数据作标准化处理后就消除了量纲不同和数量级的差异所带来的影响。