一种电子回焊炉的炉温曲线模型

Furnace Temperature Curve Model of an Electronic Reflow Furnace

摘要: 在实际工业生产中，回焊炉内并不是恒温，而是根据处理工件的流程划分了不同的温区。在已知某种电子回焊炉部分内部温度数据的基础上，通过数据分析，提出了“工件在炉内升温和降温速率与它和各温区的温差有关”的假设。由此得出了升温速率与温差的函数关系式。此关系式可以应用于矫正各温区交界处的实际温度。进一步地，还可以将原始数据代回，以温度变化速率为决策变量，建立线性规划模型，根据实际需要控制工件的过炉速度，达到节能的效果。

Abstract: In actual industrial production, the temperature in the reflow furnace is not constant, but different temperature zones are divided according to the process of processing workpieces. On the basis of knowing some internal temperature data of an electronic reflow furnace and through data analysis, the hypothesis that “the heating and cooling rate of workpiece in the furnace is related to the temperature difference between it and each temperature zone” is put forward. The functional relationship between heating rate and temperature difference is obtained. This relationship can be applied to correct the actual temperature at the junction of each temperature zone. Furthermore, the original data can be substituted, and the linear programming model can be established with the temperature change rate as the decision variable to control the passing speed of the workpiece according to the actual needs, so as to achieve the effect of energy saving.

1. 问题描述

在工业中，对器件进行焊接时会将焊接炉内部分为预热区、恒温区、回焊区和冷却区等多个温区，各温区温度不尽相同。焊接时需要设定各温区的温度和控制经过焊接区的速度，使其不至于急剧升温造成器件产生不良加热反应，又不会长时间停留在炉内时间过长影响元件精度。

2. 问题分析

炉温曲线是电路板温度—时间的曲线，电路板温度变化速率和电路板本身与回焊炉内部温差存在一次函数关系，在不同时间到达回焊炉不同的位置温度也会有不同，在综合以上关系建立炉温曲线，又因为知道传送带速度，即可求出电路板到达某一位置对应的时间，在炉温曲线内即可找出对应的温度。

由于总路程固定，传送带速度与通过回焊炉所用时间成反比，传送带的最大速度，可转化为电路板通过回焊炉最短的时间。压缩时间，即让升温速率增大，处于某一状态的时间缩短，在制程界限内，可求出电路板通过回焊炉的最短时间，进而可得最大传送带过炉速度。

在实际生产中，理想的炉温曲线应使超过217℃到峰值温度所覆盖的面积最小，即设定小温区温度，改变传送带速度，让温度达到的峰值在制程界限内尽可能的小，让温度超过217℃的时间尽量的短，在尽可能的同时满足这两个条件下即可求出最优炉温曲线，再用积分方法求相应面积。

3. 模型假设

3.1. 模型的假设

1) 焊接区域的温度不会反向影响环境温度；

2) 焊接区域的升温(和降温)速率只与两个物体之间的温度差有关；

3) 焊接区域的厚度忽略不计；

4) 回焊炉启动后，炉内空气温度会在短时间内达到稳定。

3.2. 符号说明

T——电路板温度；

t——时间；

V——电路板升温速率；

T₀——小温区温度；

l——距离。

4. 模型的建立、求解与分析

设某时刻该工件温度为 $T\left(t\right)$，设升温速率为alpha，设降温速率为Beta，该时刻所在温区的温度为 $T_0$，则温区内温度与工件的温差为

$\Delta T=T_0-T\left(t\right)$ (1)

设升温与降温速率与环境温度、工件温度的温差成正比。经过 $\Delta t$ 时间后：

$T\left(t+\Delta t\right)-T\left(t\right)=\text{alpha}\ast \left[T_0-T\left(t\right)\right]\ast \Delta t$ (2)

微分形式为：

$\frac{\text{d}T\left(t\right)}{\text{d}t}=\text{alpha}\ast \left(T_0-T\left(t\right)\right)$ (3)

由常数变易法公式 $y={\text{e}}^{{\displaystyle \int P\left(x\right)\text{d}x}}\left({\displaystyle \int Q\left(x\right){\text{e}}^{-{\displaystyle \int P\left(x\right)\text{d}x}}\text{d}t}+\tilde{c}\right)$ 解得：

$T\left(t\right)=T_0-c\ast {\text{e}}^{-\text{alpha}\ast t}$ (4)

4.1. 模型完善

由于各温区设定温度不完全一样，现以温区温度分布分段 [1] 讨论：

以工件运动方向为x轴正方向，以炉前区域的起点为原点，建立平面直角坐标系；以横坐标代表回焊炉内部个点位置坐标，纵坐标代表各点温度；假设在每个小温区内部各点温度相同，均为系统设定的区域温度；假设在两温区间的间隙温度是坐标的线性函数，且每一间隙的起点温度与终点分别为其前一温区和后一温区的区域温度。

特别地，炉前区域和炉后区域视为前一温区或后一温区为炉内环境温度的特殊间隙；工件刚进入炉内即开始计时；设炉前炉后区域长度为 $l_0$，小温区长度为 $l_1$，温区间间隙长度为 $l_2$ ；每一温区记为 $a_n\left(n=1,2,\cdots ,11\right)$ ；每一间隙记为 $b_n\left(n=1,2,\cdots ,10\right)$ ；炉前区域和炉后区域分别记为 $b_0,b_{11}$ ；第i温区的环境温度记为 $T_i$ ；对炉前区域：环境温度曲线的两端点为： $\left(0,T_0\right),\left(l_0,T_1\right)$，到达炉前区域起点的时刻恰为计时起点，t时刻工件所在位置的横坐标为： $x^{\ast }=vt$。

环境温度随坐标的变化函数为：

$T_0\left(t\right)=\frac{T_1-T_0}{l_0}x+T_0$ (5)

t时刻的环境温度为： $T^{\ast }{}^{\prime }=\frac{T_1-T_0}{l_0}vt+T_0$。

对温区 $a_n\left(n=1,2,\cdots ,11\right)$，设前温区的温度为 $T_n$，后温区的温度为 $T_{n+1}$。

工件被传送到温区 $a_n$ 的起点时，经过了 $n-1$ 个温区和间隙。

走过的路程为： $x_{01n}=\left(n-1\right)\left(l_1+l_2\right)+l_0$。

此刻的时间为： $t_{01n}=\frac{x_{01n}}{v}=\frac{\left(n-1\right)\left(l_1+l_2\right)+l_0}{v}$。

则：在t时刻，此时工件所在的位置的横坐标为： $x^{*}=v\ast t$。

此时环境的温度为 $T_n$，

$T\left(t+\Delta t\right)-T\left(t\right)=\text{alpha}\ast \left[T_n-T\left(t\right)\right]\ast \Delta t$ (6)

$\frac{\text{d}T\left(t\right)}{\text{d}t}=\text{alpha}\ast \left[T_n-T\left(t\right)\right]$ (7)

$T\left(t\right)=T_n+c{\text{e}}^{-{\alpha }_{n}t},T\left(t_{01n}\right)=T_n$ (8)

对间隙 $b_n\left(n=1,2,\cdots ,11\right)$。

设前一温区的温度为 $T_n$，后一温区的温度为 $T_{n+1}$。

工件被传送到间隙 $b_n$ 的起点时，经过了n个小温区， $n-1$ 个间隙，则间隙的温度曲线的两端点为： $\left(n{l}_1+n{l}_2-l_2+l_0,T_n\right),\left(n{l}_1+n{l}_2+l_0,T_{n+1}\right)$。

设温度随坐标的变化函数为： $T_n=kx+b,k_n=\frac{T_{n+1}-T_n}{l_2}$，

$\begin{array}{c}b=T_{n+1}-\frac{T_{n+1}-T_n}{l_2}\left(n{l}_1+n{l}_2+l_0\right)\\ =T_{n+1}-\left(n+n\ast \frac{l_1}{l_2}+\frac{l_0}{l_2}\right)\left(T_{n+1}-T_n\right)\end{array}$

$T=\frac{T_{n+1}-T_n}{l_2}\ast x+T_{n+1}-\left(n+n\ast \frac{l_1}{l_2}+\frac{l_0}{l_2}\right)\left(T_{n+1}-T_n\right)$ (9)

工件到达间隙 $b_n$ 时，走过的路程为此处的坐标，即

$x_{02n}=n{l}_1+n{l}_2-l_2+l_0$ (10)

此刻的时间为：

$t_{02n}=\frac{x_{02n}}{v}=\frac{l_0+n{l}_1+n{l}_2-l_2}{v}$ (11)

则有：在t时刻，此时工件所在位置的横坐标为：

$x^{*}=x_{02n}-l_0+v\ast \left(t-t_{02n}\right)=vt$ (12)

此处的环境温度：

$T^{*}=\frac{T_{n+1}-T_n}{l_2}\ast vt+T_{n+1}-\left(n+n\ast \frac{l_1}{l_2}+\frac{l_0}{l_2}\right)\left(T_{n+1}-T_n\right)$

故有：

$\frac{\text{d}T\left(t\right)}{\text{d}t}=\text{alpha}\ast \left[T^{*}-T\left(t\right)\right],T\left(t_{02n}\right)=T_n$ (13)

设炉前区域、第一到第五温区、第六温区、第七温区、第八第九温区、第十到炉后区域工件温度随温区温度、传送速度、升温速率、降温速率和时间的函数分别为： $T0,T1,T6,T7,T8,T10$。则可解得其表达式为：

$\begin{array}{c}T0=\left(T_0\ast l_0-T_0\ast t\ast v+T_1\times t\times v\right)/l_0-\left(T_1\ast v{T}_0\ast v\right)\ast {\text{e}}^{\left(-\alpha t\right)}\\ \ast \left(T_0\times v-T_1\times v-l_0+T_0\times \alpha \times l_0\right)/\left(l_0\times \alpha \right)\end{array}$ (14)

$T1=T_1-{\text{e}}^{\left(\alpha \times l_0/v\right)}\times {\text{e}}^{\left(-\alpha t\right)}\left(T_1-a\right)$ (15)

$T6=T_6-{\text{e}}^{\alpha \left(l_0+5l_1+5l_2\right)/v}\times {\text{e}}^{\left(-\alpha t\right)}\left(T_6-b\right)$ (16)

$T7=T_7-{\text{e}}^{\left[\alpha \left(l_0+6l_1+5l_2\right)/v\right]}\times {\text{e}}^{\left(-\alpha t\right)}\left(T_7-c\right)$ (17)

$T8=T_8-{\text{e}}^{\left[\alpha \left(l_0+7l_1+6l_2\right)/v\right]}\times {\text{e}}^{\left(-\alpha t\right)}\times \left(T_8-d\right)$ (18)

$T10=T_{10}-{\text{e}}^{\left[\alpha \left(l_0+\left(183\times l_1\right)/20+9\times l_2\right)/v\right]}\times {\text{e}}^{\left(-\alpha t\right)}\times \left(T_{10}-e\right)$ (19)

其中：

$a=T_0\left(t=l_0/v\right)$ (20)

$b=T_1\left(t=\left(l_0+5l_1+4l_2\right)/v\right)$ (21)

$c=T_2\left(t=\left(l_0+6l_1+5l_2\right)/v\right)$ (22)

$d=T_3\left(t=\left(l_0+7l_1+6l_2\right)/v\right)$ (23)

$e=T_4\left(t=\left(l_0+7l_1+6l_2\right)/v\right)$ (24)

4.2. 数据处理求参数

物体吸热(或散热)速度与两个物体之间的温度差、周围的环境、两个物体的物理性质和化学性质等有关。考虑到回焊炉给内部焊接物体加热时，物体是确定不变的，因此可以根据已给温区温度下工件温度随时间变化的数据分析得出物件的升温速率和降温速率。

由于假定焊接区域的升温(或降温)速率只与两个物体之间的温度差有关，由于各区间温度不相等，受传送方向影响，气流会从前方小温区流入后方，即后方小温区有部分区间无法达到设定温度 [2]。假设小温区受流经气流的影响恰在小温区中点时达到设定温度，且两设定温度之间温度差与距离差成正比，即温度随距离的变化呈现一次函数关系，得到预设温度、实际温度与时间距离的图像如图1：

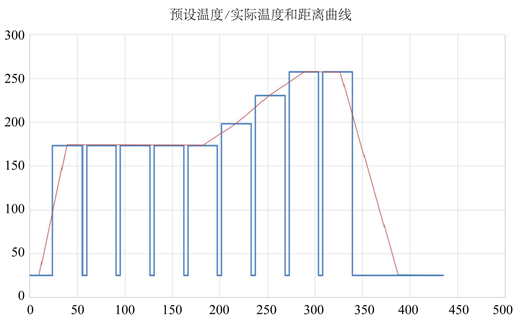
Figure 1. The curve of preset/actual temperature and distance

图1. 预设温度/实际温度与距离曲线

因各温区边界附近的温度可能受到相邻温区温度的影响，我们找了两段实际环境温度稳定，且与小温区温度一致的区域分别用于拟合升温(和降温)速率与温度差的关系。小温区2、3、4用于拟合升温速率与温度差的关系，小温区11和炉后区用于拟合降温速率与温度差的关系。

选择小温区2、3、4是因为，小温区1和5的温度与小温区2、3、4的温度相同，因此小温区2、3、4的边界不会受到相邻温区温度的影响。而小温区2、3、4中相邻小温区之间的间隙长度(5 cm)比温区长度(30.5 cm)小很多，且间隙温度(25℃)与小温区2、3、4的(175℃)温度差很大，可认为小温区2、3、4的边界温度不会受到间隙温度的影响。

选择小温区11和炉后区是因为，从温区10开始，环境设定温度保持25℃不变，小温区11的边界温度不会受到相邻温区10的影响。

对附件中的数据进行处理，计算小温区2、3、4，小温区11和炉后区的温度变化速率与温差，使用EXCEL软件进行拟合。通过增减用于拟合的数据，寻找方法最小，即拟合效果最好的一组数据。拟合结果如图2、图3所示。

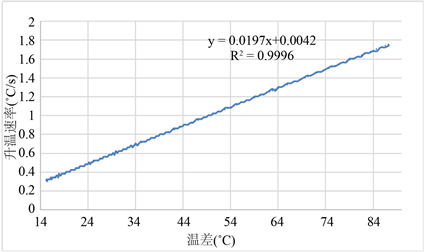
Figure 2. Fitting results of the relationship between heating rate and temperature difference

图2. 升温速率与温差关系的拟合结果

Figure 3. Fitting relation between cooling rate and temperature difference

图3. 降温速率与温差关系的拟合关系

拟合结果为：

升温速率(y)与温差(x)关系为： $y=0.02x+0.0042$ ；

降温速率(y)与温差(x)关系为： $y=0.0086x-0.2003$。

即

焊接区域温度升高时，

$T^{\prime }\left(t\right)=\frac{T\left(t+0.5\right)-T\left(t\right)}{0.5}=0.0197\ast \left(T_0-T\left(t\right)\right)+0.0042$

焊接区域温度降低时，

$T^{\prime }\left(t\right)=\frac{T\left(t+0.5\right)-T\left(t\right)}{0.5}=0.0086\ast \left(T_0-T\left(t\right)\right)-0.2003$

由此得到升温速率和降温速率常数：

$\text{alpha}=0.0197,\text{Beta}=0.0086$ (25)

对附件中的数据进行处理 [3]，计算除上述区域外的温度变化速率，带入公式(1) (2)得到每一时刻环境温度的实际值，如图4所示。

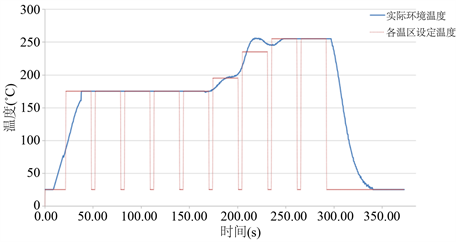
Figure 4. Comparison between the actual ambient temperature and the set temperature in each temperature zone

图4. 实际环境温度和各温区设定温度的对比图

根据图4可以看出，在小温区1的中间位置处，炉内实际温度升至小温区1的设定温度。在小温区11的中间位置处，炉内温度降至小温区的设定温度。由此我们认为，当相邻温区温度相差很大时，一半的小温区的温度会受到相邻温区温度的影响。

代入所给温区温度值，得到焊接区域中心的温度变化情况：

炉前区域

$\begin{array}{c}T0=\left(25\ast 25-25\ast t\ast 1.3+175\ast t\ast 1.3\right)/25-(175\ast 1.3-25\ast 1.3+\exp \left(-0.0197\ast t\right)\\ \ast \left(25\ast 1.3-175\ast 1.3-25\ast 0.0197\ast l_0+25\ast 0.0197\ast l_0\right))/\left(0.0197\ast l_0\right)\end{array}$

第一到第五温区

$T1=175-\exp \left(\left(0.0197\ast l_0\right)/1.3\right)\ast \exp \left(-0.0197\ast t\right)\ast \left(T_1-a\right)$

第六温区

$T6=T_6-\exp \left(\left(0.0197\ast \left(l_0+5\ast l_1+5\ast l_2\right)\right)/1.3\right)\ast \exp \left(-0.0197\ast t\right)\ast \left(T_6-b\right)$

第七温区

$T7=T_7-\exp \left(\left(0.0197\ast \left(l_0+6\ast l_1+5\ast l_2\right)\right)/1.3\right)\ast \exp \left(-0.0197\ast t\right)\ast \left(T_7-c\right)$

第八九温区

$T8=T_8-\exp \left(\left(0.0197\ast \left(l_0+7\ast l_1+6\ast l_2\right)\right)/1.3\right)\ast \exp \left(-0.0197\ast t\right)\ast \left(T_8-d\right)$

第十十一温区及炉后区域

$T10=T_{10}-\exp \left(\left(0.0197\ast \left(l_0+\left(183\ast l_1\right)/20+9\ast l_2\right)\right)/1.3\right)\ast \exp \left(-0.0197\ast t\right)\ast \left(T_{10}-e\right)$

通过matlab进行分段拟合，得到图5：

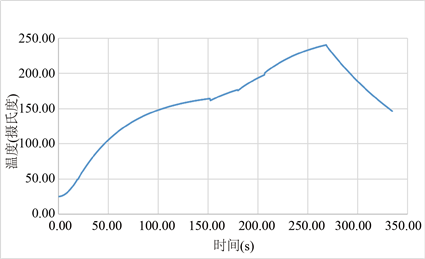
Figure 5. Results of furnace temperature curve

图5. 炉温曲线结果

特定点的温度：

通过查阅输出结果得到：

小温区3中点温度为139.28摄氏度；

小温区6中点温度为170.63摄氏度；

小温区7中点温度为190.19摄氏度；

小温区8结束处温度为222.76摄氏度。

针对制程界限的限制 [4]，建立数学规划模型：

令 $T=150$，解得 $t_1,t_2$ ；令 $T=190$，解得 $t_3,t_4$ ；令 $T=217$，解得 $t_5,t_6$

$\max v=f(\; t\; )$

$\text{s}\text{.t}\text{.}\{\begin{array}{l}\left|T^{\prime }\right|\le 3\\ {t^{\prime }}_1=\min \left\{t_1,t_2\right\}\\ {t^{\prime }}_2=\min \left\{t_3,t_4\right\}\\ \left|{t^{\prime }}_1-{t^{\prime }}_2\right|\ge 60\\ T_{\max }\ge 240\\ T_{\max }\le 250\end{array}$ (26)

解得：

$v_{\max }=1.44\text{cm}/\text{s}$

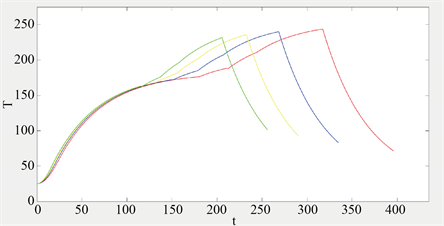
Figure 6. Furnace temperature curves corresponding to different speeds

图6. 不同速度对应的炉温曲线

据分析，在其他条件不变的条件下传送带速度越大，峰值越低，超过217℃的时间就越短，超过217℃到峰值温度所覆盖的面积(图6中阴影部分)就越小。