基于优化灰色模型算法的能源需求预测分析与应用

Analysis and Application of Energy Demand Forecasting Based on Optimized Grey Model Algorithm

摘要: 在信息化数字化的大环境下，实现能源管理系统的在线监测办法无形中成为了企业能源管理最基础的措施。而系统中的能源需求预测功能为企业的节能降耗提供最有力的数据支撑。为提高预测准确率，本文提出了一种改进的多维灰色模型能源预测算法，先使用指数加权方式进行源特征数据处理增加趋势平滑度，再用自适应粒子群与多维灰色模型算法组合，使预测的精度在原始数据不完整的情况下达到最高，为能源信息化水平不足提供了新的解决思路，解决了企业的系统优化，能源调度和管理的问题。将提出的改进算法在实际的企业项目中运行，结果显示：优化后的自适应粒子群多维灰色模型预测算法正确率最高可达到93.573%，比传统的预测算法精确度提高约36%左右。

Abstract: In the information and digital environment, the online monitoring method of energy management system has virtually become the most basic measure of enterprise energy management. The energy demand prediction function in the system provides the most powerful data support for energy conservation and consumption reduction of enterprises. In order to improve the prediction accuracy, this paper proposes an improved multidimensional grey model energy prediction algorithm. Firstly, the exponential weighting method is used to process the source characteristic data to increase the trend smoothness, and then the adaptive particle swarm optimization and multidimensional grey model algorithm are combined to maximize the prediction accuracy when the original data is incomplete, It provides a new solution for the lack of informatization of energy data, and solves the problems of enterprise system optimization, energy scheduling and management. The results show that the accuracy of the optimized adaptive particle swarm multidimensional grey model prediction algorithm can reach 93.573%, which is about 36% higher than that of the traditional prediction algorithm.

1. 引言

中国已经迅速成为能源消耗量最大的国家。2019年全年能源消费总量达48.6亿吨标准煤，比上年增长3.3%，以钢铁行业为例：2020年中国的粗钢产量达10.65亿吨，占全球粗钢产量的一半以上，中国钢铁行业的能耗约占全国总能耗的8.9% [1] [2]。

这些惊人的数据都表明着传统工业制造业能源消耗和二氧化碳排放都对地球造成了巨大的压力。对于这种高耗能企业来说，产销，季节性周期，环境因素，国家政策等因素都对能源损耗有不同权重的影响，选择合适的能源预测方法，结合企业运行的能源需求数据，预测未来一段时间的能源损耗情况，进而提高能源利用率，促进企业进行能源优化调度，以达到节能减排，提高生产效率，减少生产成本的目的 [3] [4]。

目前进行能源预测的方法有很多 [5] [6]，综合运用系统动力学模型、灰色系统模型、向量自回归模型、变权重组合预测模型等。因样本量少，不需要考虑特征数据的分布状态和趋势，因此对灰色模型进行能源需求预测进行研究分析。为提高预测精确度，本文提出的改进灰色模型也是基于这几个方面的缺陷。

传统的灰色模型理论是由我国学者邓聚龙先生于1982年提出的，主要用来研究样本信息匮乏的数据预测问题，根据部分已知的信息推算出系统发展规律，对未来状态做出定量考察。传统的灰色模型预测算法有着很多影响预测结果的问题，原始数据序列的光滑度，数据的级别偏差，多维自变量因素。张怡 [7] 提出一种将X(1)的第n个分量作为灰色微分模型的初始条件与优化背景值相结合的方式改进GM(1,1)。谢乃明 [8] 用麦克劳林公式解释了传统灰色模型不稳定的原因，提出一种离散预测灰色模型(DGM(1,1))。陈淑燕 [9] 提出嵌入型，并联和串联型三种灰色模型预测结构与神经网络进行组合，在高速公路断面实时交通量数据中进行结果验证。牛东晓 [10] 考虑两种非线性趋势的复杂季节型负荷预测问题，对于这种具有波动性趋势的电力负荷，提出一种季节型负荷预测的组合优化灰色神经网络模型，经实验证明该模型兼顾了季节型和同季波动性的特性，对电力负荷预测提供了一个新颖精确度高的方法。自适应粒子群算法 [11] 是一种通过设定迭代终止条件来在随机生成的粒子中求解出最优解。本文所提出的优化多维灰色预测模型其实是利用自适应粒子群算法收敛速度快，全局优化能力强的优点求解灰色模型中的参数，提高模型的预测精度。

2. 能源预测算法简述

2.1. 传统灰色模型算法

能源管理系统是针对明确的高耗能企业进行个性化能源管理，因此针对能源预测功能所用的模型必须具有广泛性的特点 [12]。我们结合所有的设计需求，最终选用灰色系统方法对能源数据进行预测。灰色预测是指采用GM(1,1)模型对系统行为特征值的发展变化进行预测。高耗能企业的能源种类并不是单一的，是一个多能源融合的数据分析。企业的能源损耗依赖于产品的生产。而产品的需求很大程度上依赖于大环境的影响。考虑这些不确定因素，综合来看，灰色系统办法处理此类问题理论上是有效的。在我们的测试过程中也被证实是有效的。

设变量的原始序列为：

$X^{\left(0\right)}=X^{\left(0\right)}\left(i\right),i=1,2,3,\cdots ,n$ (1)

首先对 $X^0$ 进行一次累加，生成的一次累加序列为：

$X^{\left(1\right)}=X^{\left(1\right)}\left(k\right),k=1,2,3,\cdots ,n$ (2)

最终的灰色预测模型序列满足以下关系：

${\hat{X}}^{\left(1\right)}\left(k\right)=\left(X^{\left(0\right)}\left(1\right)-u/a\right)\ast {\text{e}}^{-a\left(k-1\right)}+u/a$ (3)

其中k为时间序列，a，u为待定系数，可以用 $\hat{a}={\left[a,u\right]}^{\text{T}}$ 来表示，并利用最小二乘法进行求解 $\hat{a}={\left(B^{\text{T}}B\right)}^{-1}{B}^{\text{T}}{Y}_n$。其中：

$B=\left(\begin{array}{cc}-1/2\left(X^1\left(1\right)+X^1\left(2\right)\right)& 1\\ -1/2\left(X^1\left(2\right)+X^1\left(3\right)\right)& 1\\ ⋮& ⋮\\ -1/2\left(X^1\left(n-1\right)+X^1\left(n\right)\right)& 1\end{array}\right)$ (4)

$Y_n={\left(X^{\left(0\right)}\left(2\right),X^{\left(0\right)}\left(3\right),X^{\left(0\right)}\left(4\right),\cdots ,X^{\left(0\right)}\left(n\right)\right)}^{\text{T}}$ (5)

经过累加后的数据序列已经失去意义，必须通过累减还原为原来数据序列：

$\{\begin{array}{l}{\hat{X}}^{\left(0\right)}\left(k\right)={\hat{X}}^{\left(1\right)}\left(k\right)-{\hat{X}}^{\left(1\right)}\left(k-1\right)k>2\\ X^{\left(0\right)}x=1\end{array}$ (6)

时间序列k递增至未来，即为预测数据。

原始数据是否可以进行灰色预测，则需要对数据进行可行性检验：

$\lambda \left(k\right)=X^{\left(0\right)}\left(k-1\right)/X^{\left(0\right)}\left(k\right),k=2,3,4,\cdots ,n$ (7)

若满足 $\lambda \left(k\right)\in \left[{\text{e}}^{-2/n+1},{\text{e}}^{2/n+1}\right]$，其中n表示原始数据序列的个数，则 $X^{\left(0\right)}$ 可建立灰色模型，进行灰色预测。

否则需要对数据进行处理，使其落在有效范围内，如平移转换：

$y^{\left(0\right)}\left(k\right)=x^{\left(0\right)}\left(k\right)+c,k=1,2,3,\cdots ,n$ (8)

此算法可实现企业的能源需求预测，也可实现在企业采取节能措施后的效果预测，或者将生产数据和设备能耗数据的关系函数数值进行预测，对设备进行全生命周期的管理，由被动维修变为主动保养，减少由于设备停摆或者老化所带来的损失。为能源系统的安全稳定和持续经济运行提供了很好的支持。

2.2. 指数加权法

GM(1,1)是一种呈指数增长模型的预测方法，其预测精确度受原始数据序列光滑度离散性的限制，提高原始数据序列光滑度的办法有指数加权法，对数变换，和开n次方等方法。对于不同趋势的原始数据，预测结果的误差率比较则不同。我们这里研究的是指数加权法。

设原始数据为：

$X^{\left(0\right)}=X^{\left(0\right)}\left(i\right),i=1,2,3,\cdots ,n$ (9)

对原始数据按照以下公式进行处理，生成新序列 $Y^{\left(0\right)}(\; i\; )$

$Y^{\left(0\right)}\left(i\right)=\alpha X^{\left(0\right)}\left(i\right)+\left(1-\alpha \right)Y^{\left(0\right)}\left(i-1\right),i=1,2,3,\cdots ,n$ (10)

将新序列带入GM(1,1)模型进行预测，获得预测序列 ${\hat{Y}}^{\left(0\right)}(\; i\; )$

$X^{\left(0\right)}\left(i\right)=\left[{\hat{Y}}^{\left(0\right)}\left(i\right)-\left(1-\alpha \right){\hat{Y}}^{\left(0\right)}\left(i-1\right)\right]/\beta ,i=1,2,3,\cdots ,n$ (11)

最后按照下列公式对序列进行还原。

在此过程中， $\alpha ,\beta$ 的参数调整控制预测结果和精度。

2.3. 多维灰色模型算法

在传统一维灰色模型的基础上，增加了相关的影响因子序列。原始数据序列为 $X^{\left(0\right)}$ 相关因素序列为：

$\begin{array}{l}{X}_2^{\left(0\right)}\left(i\right)=\left(X_2^{\left(0\right)}\left(1\right),X_2^{\left(0\right)}\left(2\right),X_2^{\left(0\right)}\left(3\right),\cdots ,X_2^{\left(0\right)}\left(n\right)\right)\\ ⋮\\ X_N^{\left(0\right)}\left(i\right)=\left(X_N^{\left(0\right)}\left(1\right),X_N^{\left(0\right)}\left(2\right),X_N^{\left(0\right)}\left(3\right),\cdots ,X_N^{\left(0\right)}\left(n\right)\right)\end{array}$ (12)

再将原始特征数据和因素数据进行累加

$X_k^{\left(1\right)}\left(i\right)={\displaystyle \underset{i-1}{\overset{n}{\sum }}{X}_k^{\left(1\right)}}\left(i\right),i=1,2,3,\cdots ,n$ (13)

紧邻均值序列计算公式为：

$Z_1^{\left(1\right)}\left(i\right)=1/2\left[X_1^{\left(1\right)}\left(i\right)+X_1^{\left(1\right)}\left(i-1\right)\right],i=1,2,3,\cdots ,n$ (14)

最后建立灰色理论方程：

$X_1^{\left(0\right)}\left(i\right)+\alpha Z_1^{\left(1\right)}\left(i\right)={\displaystyle \underset{k-2}{\overset{N}{\sum }}{b}_k{X}_1^{\left(0\right)}}\left(i\right),i=1,2,3,\cdots ,n$ (15)

2.4. 自适应粒子群算法

在迭代中不断缩小种群搜索空间，使粒子能够跳出之前的搜索最优解，在更大的空间开展搜索，增加搜索到最优解的可能性。第i个粒子在L维空间的搜索位置是X_i，他所经历的最好的位置是 $Pbes{t}_i=\left(p_{i1},p_{i2},\cdots ,p_{il}\right)$，整个粒子群所经历最好的位置为 $Gbes{t}_i=\left(p_{k1},p_{k2},\cdots ,p_{kl}\right)$。

$V_i^{\left(t+1\right)}=W{V}_i^{\left(t\right)}+c_1{r}_1\left(Pbes{t}_i^{\left(t\right)}-X_i^{\left(t\right)}\right)+c_2{r}_2\left(Gbes{t}_g^{\left(t\right)}-X_i^{\left(t\right)}\right)+\cdots$ (16)

$X_i^{\left(t+1\right)}=X_i^{\left(t\right)}+V_i^{\left(t+1\right)}$ (17)

其中 $c_1,c_2$ 是加速度因子， $r_1,r_2$ 是[0,1]之间的随机数， $X_i^{\left(t\right)}$ 和 $V_i^{\left(t\right)}$ 分别是第i个粒子的当前位置和飞行速度。

3. 实验仿真结果与分析

对于应用型的系统设计来说，我们需要考虑到物理层数据采集不完整或者运行初期样本数量少的情况，为满足客户对这一功能的使用，基于对原始数据样本要求不高，但能预测出相对误差较小的能源损耗趋势。因此本文选择研究灰色模型来进一步改进提高预测精确度。根据钢铁行业的能源损耗监测的结果来看，电力负荷类型复杂，对电力数据进行预测分析是整个系统的重头戏。为验证对能源需求预测算法的准确度，我们对比了传统灰色模型，指数加权优化灰色模型和自适应粒子集群优化多维灰色模型的预测误差率结果。选取变电站南钢2P64线——表记耗电量原始特征数据。在预测之前对样本选择做了限制：原始数据进行时间序列的特征提取，系统的数据采集频率是每分钟，因减少差异性所以设定同一个区域同一个设备级别的：

· 小时级别的(这是每天的第几个小时)；

· 天级别的(这是每周的第几天，每月的第几天，每年的第几天)；

· 周级别(星期几，每年的第几周)；

· 月级别(哪一月，是否是月初，是否是月末)；

· 季度级别(对系统运行时间，采集到的数据周期跨度有要求)；

· 年度级别(对系统运行时间，采集到的数据周期跨度有要求)。

我们选取2021年1月份到3月份的每周一上午10:00的变电站南钢2P64线电力损耗数据，具体数据如下表1所示：

Table 1. Power consumption data of substation Nangang 2P64 line

表1. 变电站南钢2P64线——表记耗电量数据

经过计算，数据满足级别要求，可选用传统灰色模型算法进行预测。预测结果的平均准确率为57.143%。经过计算，预测处理的能源数据的总体误差很大，预测准确率太低，数据趋势也与实际情况有很大出入。作为预测模型进行能源损耗数据的预测是不可取的。传统灰色模型预测误差分析如下表2所示：

Table 2. Prediction and analysis of traditional Grey Model

表2. 传统灰色模型预测分析表

为提高预测准确度，我们对原始数据的平滑度进行优化。通过调节指数加权算法中的α，β参数，优化后的一维灰色模型预测结果平均准确率为67.376%。考虑的可能原因如下：对于钢铁行业来说，能源损耗与产销，与季节性周期，环境因素，国家政策等因素有不同权重的影响，这是传统灰色模型的理论缺点。随后列举出影响能源需求数据的所有因素，按照能源管控平台所能提供的其他因素数据，我们选取企业运行温度，生产产量作为影响因子序列，用自适应粒子群求解粒子的位置和更新速度，通过不停地迭代，确定Pbesti，Gbesti和w，输出灰色模型的参数带入目标函数。

利用表1的原始数据进行实验验证，实验结果如图1所示，其中Testing data1为指数加权改进的灰色模型预测结果，Testing data2为自适应粒子群多维灰色模型的预测结果：

由图知，原始数据为非单调增长趋势函数类型，传统的灰色模型预测出来的曲线趋势近似指数函数。这也是传统灰色模型的预测缺陷，即对原始数据的要求严格。当特征数据呈指数趋势，预测效率是最好的。我们通过指数加权的方式对原始数据的平滑度进行处理，改进后的预测精确度和传统模型比，有了初步的提高。而自适应粒子群多维灰色模型预测结果是最好的，整体趋势更接近于原始特征数据，在多个时间节点上都更接近于原始数据。经过计算，预测准确度高达93.573%。

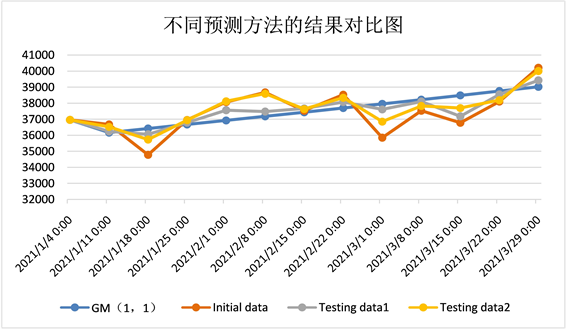
Figure 1. Broken line comparison of results of several different prediction algorithms

图1. 几种不同预测算法的结果折线对比图

4. 总结

就目前的工业企业来说，生产，供应，销售，管理等各个环节都存在一定的能源浪费 [13]。这些节能减排需求和运行短板，使得企业生产效率低下，能源浪费 [14] [15]。本文所设计的自适应粒子群与灰色模型结合，在实际的非单调增长趋势的能源数据预测中，得到了很好的应用，改善了传统的灰色模型预测数据的局限性。该模型运用在能源管理系统中，可为企业提供最有力的数据支持，在满足企业生产的前提下，最大限度地进行能源调度，实现节能减排，优化生产过程，减少生产成本。

该算法在实验中虽然大大提高了预测准确度，但是影响因素的选择有待考量。生产企业的电力损耗相关性因素有待挖掘。原始数据的不同曲线趋势与预测模型的选择的相关性也是值得研究的话题。