1. 引言
涡致振动是海底悬跨管道的主要振动形式。当漩涡脱落的频率接近悬跨管道自振频率时,悬跨管道的振动会使漩涡脱落的频率固定在悬跨管道自振频率附近,而不按其本身的频率发放,此即为频率“锁定”现象。由涡致振动以及频率“锁定”导致的结构失稳以及疲劳破坏是海底管线破损的重要形式,而这种破坏形式在浅海区尤其明显。过去的几十年里,国内外学者针对悬跨管道振动的一系列相关问题开展了大量数值分析、理论与实验研究,取得了一定的研究成果。
国外研究起步较早,以挪威海洋技术研究所(MARINTEK)和挪威科技大学(NTNU)在该领域做出的贡献最为突出 [1]。1997年,Larsen领导的研究团队研发了VIVANA商业软件,该软件能够实现海底悬跨管道和海洋立管涡激振动分析和疲劳分析 [2]。为了进一步完善软件功能,2015年,Larsen等人 [3] 使用了频域和时域方法研究悬跨管道涡激振动现象。2017年,Larsen领导的课题组人 [4] 利用非线性时域方法进一步研究了悬跨管道的涡激振动。2018年,Furns和Berntse [5] 假设IL和CF挠曲是通过任意时刻的轴向张力耦合的,研究了海流作用下悬跨管道IL方向和CF方向运动的耦合性,结果表明悬跨管道涡合效应明显,不可忽略。我国学者余建星 [6] [7] 等人根据建立的悬跨管道的非线性涡激振动方程对涡激振动疲劳可靠度进行了研究。黄维平 [8] 等人对输液模型管道进行了涡激振动实验研究,根据实验结果修正了涡激升力模型中IL方向上流速的影响。
2002年,挪威船级社发布DNV-RP-F105 [9] 给出是否需对涡激振动及波浪导致海管的疲劳问题进行详细疲劳寿命计算的判断准则,准则的核心是判断固有频率需要满足的条件 [10],研究表明判断准则中应采用悬跨管道工况条件下的固有频率,论文采用数值方法研究了不同端部约束条件、不同悬跨长度、不同内压荷载、不同轴向受力等工况条件对悬跨管道固有频率的影响。
2. 悬跨管道涡激振动仿真模型的建立
考虑到管线内流影响的复杂性,仅考虑管线控制方程,亦不考虑固体管道和管内流体的流固耦合现象,采用文献 [11] 的三维弹性动力学的基本方程:
平衡方程:
(1)
几何方程:
(2)
物理方程:
(3)
边界条件:
(在位移边界上)
(在应力边界上)
初始条件:
(4)
(5)
式中:ρ是物质密度;μ是阻尼系数;
为弹性常数;
和
分别是
对t的一次导数和二次导数。
3. 悬跨管道涡激振动数值分析可靠性验证
3.1. 悬跨管道模态分析网格无关性分析
如不做特殊说明,研究悬跨管道物理参数如表1所示:

Table 1. The physical parameters of span ning pipeline
表1. 悬跨管道物理参数
图1可以看出,径向网格密度对悬跨管道模态分析几乎没有影响;随着环向网格密度的增加,一阶、二阶模态自振频率逐渐升高;而随着轴向网格密度的增加,一阶、二阶模态自振频率逐渐降低。依据图1的内容,本文选择网格密度80。

Figure 1. The impact on modal analysis of span ning pipeline mesh density
图1. 网格密度对悬跨管道模态分析的影响
3.2. 涡激振动数值分析实验验证
表2,表3分别表示不同雷诺数对悬跨管道升力系数、曳力系数的影响,从表2,表3可以看出,本文的计算与已有公布的研究成果较为接近,只是较其中3~4例计算结果偏大,因此可认为本文的计算结果能够满足研究要求。

Table 2. The effects on CL of Reynolds number
表2. 雷诺数对升力系数的影响

Table 3. The effects on CD of Reynolds number
表3. 雷诺数对曳力系数的影响
4. 悬跨管道涡激振动模态分析
4.1. 不同端部约束条件悬跨管道模态分析
悬跨管道端部约束条件是管跨涡激振动的重要研究内容,也是决定悬跨管道涡激响应的重要因素。
图2描述了悬跨管道各阶自振频率随线性弹簧约束条件的变化,从图2可以看出,变化曲线以对数函数的方式呈现。

Figure 2. The impact on modal analysis of span ning pipeline with different restraint
图2. 不同端部约束悬跨管道模态分析图
悬跨管道端部约束条件对其涡激振动有重要影响,但当弹簧刚度达到一定数值以后,悬跨管道各阶自振频率变化已经不大。
4.2. 不同悬跨长度管道模态分析
图3描述了悬跨管道各阶自振频率随管道悬跨长度的变化,从图3可以看出,变化曲线以乘幂函数的方式呈现,悬跨管道横向和顺向振动频率的变化规律和变化量一致;随着悬跨长度的增加,管道各阶振动频率几乎是成倍的减小,影响非常明显。

Figure 3. The impact on modal analysis of span ning pipeline with different span ning length
图3. 不同悬跨长度管道模态分析
4.3. 不同内压荷载悬跨管道模态分析
图4描述了悬跨管道各阶自振频率随管道内压荷载的变化,图4曲线变化表明内压荷载对悬跨管道各阶自振频率的影响存在临界值,超过临界值自振频率快速升高,随着内压荷载的增加,悬跨管道横向和顺向振动频率逐渐增大,但当内压荷载较小时,悬跨管道自振频率升高有限,只有当内压荷载达到某一高值,约3000 kPa后,悬跨管道各阶自振频率才会有明显的提升。
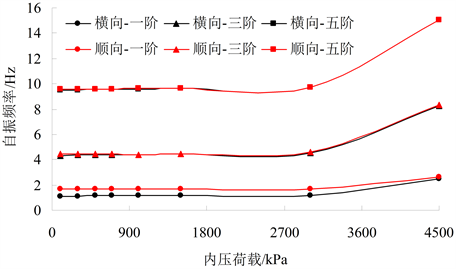
Figure 4. The impact on modal analysis of span ning pipeline with different internal pressure
图4. 不同内压荷载悬跨长度管道模态分析图
4.4. 不同轴向受力悬跨管道模态分析
4.4.1. 轴向拉力
图5描述了悬跨管道各阶自振频率随管道轴向拉力的变化,从图5可以看出,悬跨管道顺向和横向五阶自振频率存在差异,一阶、三阶自振频率的变化一致。从图中可以看出,当轴向拉力不太高时,悬跨管道自振频率随轴向拉力呈现线性函数的变化趋势,随着模态阶数的提高,线性函数变化的临界轴向拉力值变小;超过线性函数变化的临界轴向拉力值,曲线变化趋势不明显;轴向拉力对悬跨管道自振频率的影响非常明显;随着轴向拉力的增加,悬跨管道横向和顺向振动频率逐渐增大,但这种影响随着模态阶数的提高而弱化。
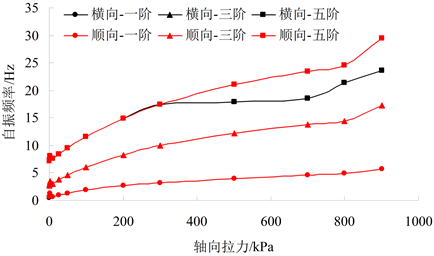
Figure 5. The impact on modal analysis of span ning pipeline with different axial tension
图5. 不同轴向拉力悬跨管道模态分析图
4.4.2. 轴向压力
图6描述了悬跨管道各阶自振频率随管道轴向压力的变化,从图6可以看出,悬跨管道自振频率随轴向拉力呈现线性函数的变化趋势;随着轴向压力的增加,悬跨管道横向振动频率逐渐减小,轴向压力越大,这种变化趋势越明显;轴向压力对悬跨管道顺向振动频率的影响较小。

Figure 6. The impact on modal analysis of span ning pipeline with different axial pressure
图6. 不同轴向压力悬跨管道模态分析图
5. 结论
1) 仿真结果实验验证证明论文采用数值仿真方法得到的悬跨管道各阶模态结果是可靠的。
2) 悬跨管道各阶模态主要受悬跨长度、轴向力、端部约束条件以及内压荷载的影响,尤其以悬跨长度、轴向力、端部约束条件的影响最为严重。
3) 悬跨长度对悬跨管道模态的影响以乘幂函数呈现,轴向力和端部约束条件悬跨管道模态的影响以对数函数呈现。
4) 内压荷载对悬跨管道各阶自振频率的影响存在临界值,超过临界值自振频率快速升高。
5) 当轴向拉力不太高时,悬跨管道自振频率随轴向拉力呈现线性函数的变化趋势,随模态阶数提高,线性函数变化的临界轴向拉力值变小。
6) 超过线性函数变化的临界轴向拉力值,曲线变化趋势不明显;悬跨管道自振频率随轴向拉力呈现线性函数变化。