气候变化情景下杨房沟水电站未来设计洪水计算

The Future Design Flood Estimation of Yangfanggou Hydropower Station under the Climate Change Scenario

摘要: 受气候变化和下垫面变化的影响，水文序列的一致性遭到破坏，传统基于水文序列一致性假设的水文频率计算方法已不再适用。针对变化环境下杨房沟水电站的非一致性设计洪水问题，采用ASD降尺度模型进行未来降水预测，基于贝叶斯模型加权平均法进行未来降水的不确定性分析，应用GAMLSS模型对洪水序列进行非一致性洪水频率分析，估算水电站未来设计洪水，为变化环境下的水电站防洪设计及防洪调度提供科学依据。

Abstract: The stationary of hydrologic series has been undermined by climate change and underlyding surface change, and the traditional hydrologic frequency calculation method based on the hypothesis of hydro-logic series stationary is no longer applicable. In view of the problem of non-stationary design flood of Yangfanggou hydropower station in the changing environment, this study uses the ASD downscaling model to forecast future precipitation, and uncertainty analysis of the precipitation based on Bayesian model averaging. Then, the future design flood of the projection is estimated by the GAMLSS model, which will provide scientific basis for design flood and flood control operation of hydropower station under changing environment.

1. 引言

水文时间序列是一定时期内气候因素、下垫面条件及人类活动等因素共同作用下的结果。传统水文频率分析工作的一个基本前提是水文序列样本满足一致性假设，然而在气候变化和人类活动的影响下，该假设越来越难满足，水文序列存在非一致性已成为不争的事实 [1]。2008年Milly [2] 就已提出：流域水文情势的变化使得水文序列的“一致性”不复存在，水文序列的一致性假设受到了质疑。

近年来，国内外对非一致性水文序列的频率计算开展了大量的研究，主要集中在以下两方面：一是基于还原/还现途径，将不同时期不同环境的水文序列还原为同分布序列 [3] [4]；二是采用时变矩法，假定水文变量的分布类型不变，分布的参数随时间或其它协变量变化 [5] [6] [7] [8] [9]。无论是“还原”还是“还现”，所推求水文序列的概率分布只能反映过去或者现状环境下的水文情势，仍然无法反映未来水文情势。时变矩法在一定程度上可以避免此问题，其中，基于位置、尺度和形状参数的广义可加模型(简称GAMLSS模型) [6]，可以建立水文变量的统计参数与协变量之间的统计关系，是目前应用最为广泛的非一致性水文频率分析方法。为此，本文选用第五次耦合模式比较计划(CMIP5)的未来3种典型排放浓度(RCP2.6, RCP4.5, RCP8.5)，采用多种全球气候模式(GCM)进行未来不同情景降水的预测，并以降水为协变量，采用GAMLSS模型进行杨房沟水电站时变设计洪水计算，为该水电站的防洪安全提供科学依据。

2. 流域概况及数据资料

2.1. 流域概况

杨房沟水电站位于四川省凉山彝族自治州木里县境内的雅砻江干流处(101˚13'E, 28˚35'N)，是雅砻江中游河段“一库七级”开发方案中的第六级水电站，上游为孟底沟水电站，下游为卡拉水电站。杨房沟水电站坝址位于雅江水文站(上游)与麦地龙水文站(下游)两个控制断面之间，集水面积为80,880 km²，设计洪峰流量为9320 m³/s，校核洪峰流量为11,200 m³/s。雅江水文站设立于1947年12月，麦地龙水文站设立于2000年6月，其中麦地龙水文站为杨房沟水电站设计代表站，该站控制面积为81,161 km²。杨房沟水电站坝址以上流域(以下简称研究区域)水系概化图如图1所示。

2.2. 数据资料

本文所用数据包括：研究区域1953~2012年的历史实测洪水资料和同期面平均年降水资料；研究区域CNRM、MIROC、CanESM和GFDL4种GCM在基准期1984~2005年的模拟降水数据，以及在未来RCP2.6、RCP4.5和RCP8.5情景下2021~2100年的模拟降水数据，由ASD降尺度模型得到，详见文献 [10]。

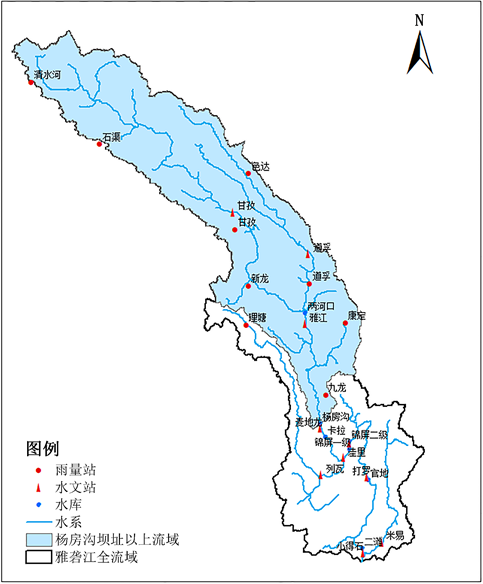
Figure 1. An overview of the water system in the basin above the dam site of Yangfanggou Hydropower Station

图1. 杨房沟水电站坝址以上流域水系概化图

3. 研究方法

3.1. BMA不确定性分析方法

贝叶斯模型加权平均方法(BMA)是一个通过加权计算不同模型的预报结果，来获取更为可靠的综合预报结果的方法 [11]。

假设D为实测序列、Q为模拟序列，K为模型数量，对实测数据和模拟序列进行正态化后可根据BMA加权平均公式求得平均预报值，BMA加权平均公式为：

$E\left(Q|D\right)={\displaystyle \underset{k=1}{\overset{K}{\sum }}p\left(f_k|D\right)}\cdot E\left[g\left(Q|f_k,{\sigma }_k^2\right)\right]={\displaystyle \underset{k=1}{\overset{K}{\sum }}{\omega }_k{f}_k}$ (1)

其中： $p\left(f_k|D\right)$ 为给定实测数据第k个模型预报 $f_k$ 的后验概率， $g\left(Q|f_k,{\sigma }_k^2\right)$ 表示均值为 $f_k$ 、方差为 ${\sigma }_k^2$ 的正态分布， ${\omega }_k$ 为第k个模型的权重。

由BMA方法求得的权重 ${\omega }_k$ 和模拟误差 ${\sigma }_k^2$ 即可采用蒙特卡罗抽样法确定预报值的不确定性区间。

3.2. GAMLSS模型

近年来，随着统计分析数据量的猛增，为克服广义线性模型和广义可加模型等相关性模型的局限性，Rigby等提出了基于位置、尺度和形状参数的广义可加模型(GAMLSS) [6]。GAMLSS模型假定变量x服从参数为 ${\theta }_i\left(i=1,2,\cdots ,p\right)$ 的分布函数，p为参数个数， $g_i\left({\theta }_i\right)$ 表示 ${\theta }_i$ 与解释变量 $Z_i$ 的单调函数关系

$g_i\left({\theta }_i\right)={\eta }_i=Z_i{\beta }_i$ (2)

式中： ${\theta }_i$ 、 ${\eta }_i$ 为长度为n的向量，n为变量x的样本长度， $Z_i$ 是 $n\times I_i$ 的解释变量矩阵， ${\beta }_i={\left({\beta }_{1i},{\beta }_{2i},\cdots ,{\beta }_{I_{i}i}\right)}^{\text{T}}$ 是长度为 $I_i$ 的回归系数向量， $I_i$ 为解释变量的个数。GAMLSS模型以 ${\beta }_i$ 的最大似然函数为目标函数，采用RS算法进行回归系数 ${\beta }_i$ 的最优值估计。

4. 未来设计洪水计算

4.1. 未来降水的不确定性分析

文献 [10] 利用ASD模型，将CNRM、MIROC、CanESM和GFDL4种GCM输出的RCP2.6、RCP4.5和RCP8.5情景下的气候因子，统计降尺度到雅砻江流域的15个气象站点，对比分析了4种GCM对研究区域的降水模拟效果。结果表明，各GCM在雅砻江流域均有一定的适用性。本文基于上述成果，进一步统计了研究区域未来不同情景下的年降水量，如图2所示。

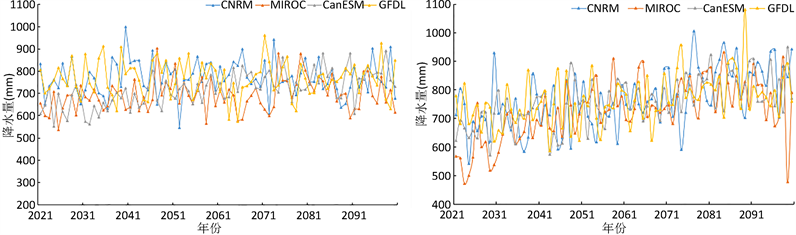(a) RCP2.6情景 (b) RCP4.5情景 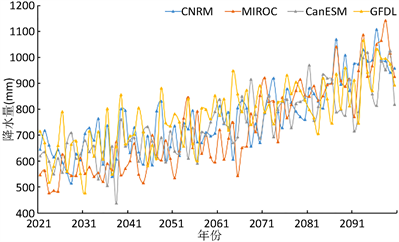(c) RCP8.5情景

Figure 2. The results of the next year's precipitation calculation of GCM in different scenarios in the future

图2. 未来不同情景不同GCM下年降水量计算结果

可以看出，尽管各GCM未来年降水的变化趋势大致相同，但每年的模拟结果差别较大，不同模式生成的未来降水存在较大程度的不确定性。利用上述4个GCM在基准期的模拟降水值及实测值，采用BMA方法对其进行不确定性分析，得出年降水的集合平均值及不确定性评价指标，如表1所示。

Table 1. Evaluation of 4 GCM and BMA annual precipitation forecast values

表1. 4种GCM和BMA年降水量模拟值不确定性分析评价表

综合分析，BMA模型的模拟精度更高，不确定性更小，可将其作为未来非一致性设计洪水的依据，BMA的模拟结果如图3所示。

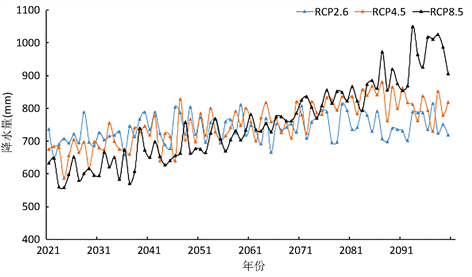
Figure 3. BMA results for precipitation in different scenarios in the future

图3. 未来不同情景下年降水量BMA结果

4.2. 非一致性水文频率分析

通过构造位置、尺度和形状参数的链接函数，建立基于P-III分布的广义可加模型，以年降水量为协变量，对杨房沟水电站洪峰序列进行非一致性水文频率分析。为使模型在不过多增加自由度的前提下仍可体现水文序列的时间变化趋势，仅考虑分布参数的线性变化情况，其中P-III分布中的形状参数非常敏感而难以估计，故将其视为固定值，不考虑该分布形状参数的非一致性变化。P-III分布的概率密度函数及其函数关系如下：

$f_x\left(x|\mu ,\sigma ,\nu \right)=\frac{1}{\sigma \mu \nu \Gamma \left(1/{\nu }^2\right)}{\left(\frac{x-\mu }{\mu \sigma \nu }+\frac{1}{{\nu }^2}\right)}^{\frac{1}{{\nu }^2}-1}\exp \left[-\left(\frac{x-\mu }{\mu \sigma \nu }+\frac{1}{{\nu }^2}\right)\right]$ (3)

式中， $\mu =Ex,\sigma =Cv,\nu =0.5Cs$，分别为P-III分布的位置、尺度和形状参数。链接函数为：

$g_1\left(\mu \right)=\ln \left(\mu \right),g_2\left(\sigma \right)=\ln \left(\sigma \right),g_3\left(\nu \right)=\nu$ (4)

当以年降水为协变量时，P-III分布的GD、AIC和SBC值如表2所示。由表2可得，以年降水量为协变量时，第三种时变参数变化情况的GD、AIC和SBC值均为最小，因此选取P-III分布中位置参数随年降水变化，尺度参数和形状参数均为常量的模型为最优非一致性模型。

Table 2. A statistical table of GD, AIC, and SBC values for the non-consistent model with precipitation as a covariate

表2. 以降水为协变量的非一致性模型的GD、AIC和SBC值统计表

(a) QQ图 (b)百分位图

Figure 4. The QQ and centile curves of the optimal non-conformity model of the flood peak flow sequence with precipitation as the covariate

图4. 洪峰流量序列以降水为协变量最优非一致性模型的QQ图及百分位图

由图4可得，残差正态QQ图显示除个别点偏离外，大部分点都分布在1:1线附近，百分位曲线图也直观展示了实测点据在不同区间的分布情况，这些都说明所选非一致性模型效果较好。表3为杨房沟站洪峰序列以年降水量为协变量时的最优非一致性GAMLSS模型残差定量评价指标。在显著性水平 $\alpha =0.05$ 时，当Filliben相关系数Fr大于临界值0.978时可认为模型通过检验。由此结果，可定量地判断出模型的总体模拟效果较好。

Table 3. The quantitative evaluation index with GAMLSS model of residual residuals of the Yangfanggou station’s Hongfeng sequence is optimal and non-consistent

表3. 杨房沟站洪峰序列最优非一致性GAMLSS模型残差定量评价指标

由GAMLSS模型可以输出P-III分布的参数与协变量的线性表达式为

$\ln {\mu }_t=6.7524+0.0024P_{t}t=1953~2012$ (5)

式中： ${\mu }_t$ 为P-III分布时变的位置参数， $P_t$ 为年降水量。由式中参数与协变量之间的关系可进行未来时期非一致性设计洪水研究。

4.3. 未来设计洪水计算

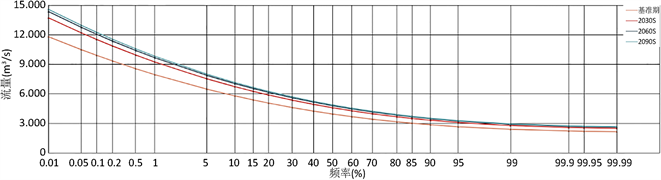
将未来2021~2100年分成3个时期，分别为2021~2050年(简称2030S)、2051~2075年(简称2060S)和2076~2100年(简称2090S)。未来设计洪水采用P-III分布计算，由于以年降水为协变量的时变设计洪水每年都是变化的，实际应用中既无必要，也难以实施，因此，可以分时期计算未来的设计洪水，其均值由式(5)得到，其中，未来年降水量为各个时期的BMA多年平均降水；未来时期的Cv和Cs采用基准期的参数值，即Cv = 0.29，Cs = 4Cv。由此可以得到未来不同情景各个时期的设计洪水频率曲线，如图5所示。

(a) RCP2.6情景 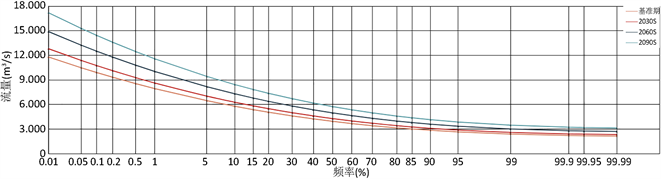(b) RCP4.5情景 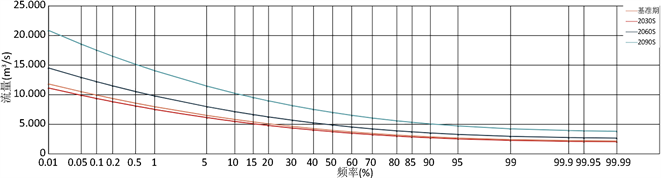(c) RCP8.5情景

Figure 5. Design flood frequency curves for each period of future scenarios

图5. 未来情景各个时期的设计洪水频率曲线

采用以年降水为协变量的GAMLSS模型进行未来设计洪水的计算，未来设计洪水一定程度上取决于BMA计算的未来年降水，未来情景下年降水预测结果如表4所示。可以看出，除RCP8.5情景下2030S时期的年降水小于基准期外，其余各个情景各个时期均大于基准期，其中RCP2.6情景下，增幅为10.30%~14.19%；RCP4.5情景下，增幅为5.93%~24.7%；RCP8.5情景下，增幅为−3.15%~36.92%。增幅最大的为RCP8.5情景下2090S时期，相比基准期增加为39.51%。由此得到的设计洪水也呈现不同程度的增加，如表4所示。可以看出，在未来情景下除RCP8.5情景下2030S时期的设计洪水和校核洪水小于基准期外，其余各个情景各个时期均大于基准期，其中RCP2.6情景下，超设计洪水的增幅为16.29%~23.61%，超校核洪水的增幅为16.57%~23.91%；RCP4.5情景下，超设计洪水的增幅为8.58%~45.79%，超校核洪水的增幅为8.84%~46.3%；RCP8.5情景下，超设计洪水的增幅为−5.85%~76.76%，超校核洪水的增幅为−5.63%~77.09%；设计洪水和校核增幅最大的均为RCP8.5情景下2090S时期，相比基准期分别增加为76.66%和77.09%。

Table 4. Future design flood and school nuclear flood calculation table

表4. 未来设计洪水和校核洪水计算结果表

5. 结论

本文以杨房沟水电站为研究对象，计算了考虑未来降水的水库设计洪水，主要研究结论如下：

1) 以年降水为协变量进行时变设计洪水计算，不仅使得模型具有一定的物理意义，更能充分利用已有的一些先验信息，提高了洪水频率计算的精度。

2) 基于基准期的最优非一致性GAMLSS模型，以BMA方法得出的未来不同情景下的年降水为协变量，对杨房沟水电站未来不同时期的设计洪水进行了计算，在一定程度上提高了未来设计洪水的可靠性。

3) 未来3种气候变化情景下，杨房沟水电站设计及校核洪水均有一定程度的增加，需加强防范。

基金项目

中国电力建设股份有限公司项目(DJ-ZDZX-2016-02)。

参考文献