1. 引言
深部高承拉含水层上采煤一直是我国向深部工作面不断拓展而出现的一些特殊地质条件下难度较大的采煤开采技术问题 [1],在煤炭安全开采中,有效防治采煤突水问题也是一个重要的采矿工程问题,且目前来说一直都未解决 [2] [3]。目前有很多相关学者提出很多理论,“关键层”理论是由中国矿业大学黎良杰、钱鸣高于早年提出,认为煤层中隔水承载力性能最强的底板隔水层为关键层 [4]。对于关键层的力学分析,通常考虑水压力作用下导致的煤层弯曲变形以及裂缝产生,因此煤层底板抵抗水压力的强度是关键。在实际运用中关键层的力学分析很重要,关键层的强度决定着顶底板的破坏形式。关于矿井工作面突水的研究已经达到了一个较为先进的水平,形成了一些比较完善的理论。可是在形成的这些突水理论中都或多或少的存在着条件的限制和相对理想化的成分。目前对关于隔水关键层的浅梁理论运用还缺乏研究,本文将关键层的厚度和跨度比模拟成于梁的高跨比,探究浅梁理论是否适合关键层的应用。目前梁在人们日常工程活动中广泛运用,在建筑的使用过程中作为主要承重和受弯构件的梁高度不断增大,当梁构件高度和跨度之比达到一定界限,即相应的高跨比大于等于0.2时,就应考虑剪切变形对挠度产生的影响,以满足精度要求,此时的梁即可认为是深梁构件,就形成高度较大的深梁结构,现阶段深梁构件由于其巨大的承载能力而得到越来越广泛的应用 [5]。梁的受力和变形分析既是力学的基础理论问题,也是工程结构设计中最关心的问题。一些学者对静定梁的受力和变形全过程进行过分析 [6] [7] [8] [9] [10]。随着工程技术的发展,应考虑剪切变形影响的深梁问题越来越多,如结构界面尺寸相对于跨径来说较大情况、梁的高阶振动、局部高度承载、弹性地基梁的地基沉降问题等问题,运用初等梁理论分析将导致计算结果偏小 [11]、计算精度不足等问题。为解决这些问题,各国学者提出了很多深梁理论 [12] [13],出现了大量研究成果和工程应用,促进了深梁理论的发展。本文将关键层模拟成固定梁,采用不同高跨比的固定梁进行研究,采用弹性力学中解决超静定梁的应力函数法以及材料力学中关于梁截面的应力计算方法,对比FLAC3D的数值解,分析关键层适用于浅梁理论的条件,作为底板突水研究的一个重要方面,可以更好地为突水事故预测提供理论支撑。
2. 模型建立
将关键层视为固定梁,研究不同高跨比下的固定梁的平面应力问题。取梁的长度为L,横截面积高为h,宽为b,梁上部承受均布荷载q的作用,高跨比h/l分别取值为0.1, 0.2, 0.3, 0.4。基于梁左端边界中点为圆心建立x, y, z坐标轴。材料力学和弹性力学均建立相同的坐标系,其固定梁平面模型图如下图1所示:
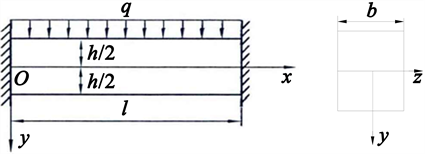
Figure 1. Plane model of fixed beam at both ends
图1. 两端固定梁平面模型
根据关键层固定梁特点,上、下边界条件为:
3. 两种算法解析解
3.1. 弹性力学解
关于两端固定梁的解,文献 [14] 给出的关于超静定梁应力解答为:
其中,
,
,
,
,
,
。
3.2. 材料力学解
关于两端固定梁的解,综合文献 [15] [16] [17] 给出材料力学关于超定梁应力解答为:
其中,
,
,
,
。
4. 算例分析
为研究不同高跨比下两种解法的应力区别,将矩形截面梁的长固定为40m。高度进行变化,取泊松比v = 0.25。弹性模量E = 20 Gpa,均布荷载q = 0.5 Mpa。将材料力学解、弹性力学的理论用matlab计算,再对比FLAC3D数值解。为验证以上两种解析解在深梁下的影响,将解析解与数值解对比成图2。为关键层是否适用浅梁理论作指导。

Figure 2. Stress model of simulated beam in water-proof key layer
图2. 隔水关键层模拟梁的受力模型
由于弹性力学解和材料力学解的剪切应力表达式是一样的,所以各高跨比取x = 15 m处节点进行比较。
1) 当h/l = 0.1时,取h = 4, L = 40
取边缘x = 0处节点和x = 15m处节点为考察点,通过弹性力学解和材料力学解得到不同高跨比条件下的正应力解和剪应力解见图3~5。
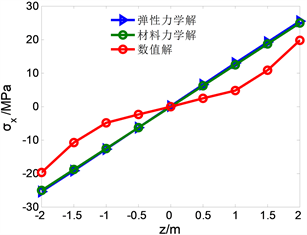
Figure 3. Change with z when x = 0 m
图3. x = 0 m时,
随z的变化
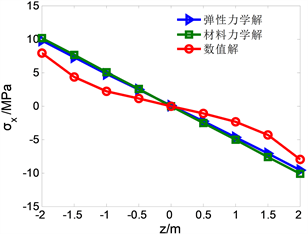
Figure 4. Change with z when x = 15 m
图4. x = 15 m时,
随z的变化
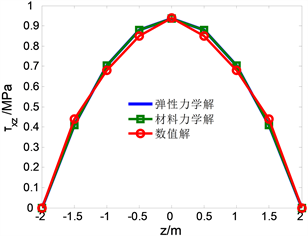
Figure 5. Change with z when x = 15 m
图5. x = 15 m时,
随z的变化
分析图3,当在支座处x = 0的时候,可看出材料力学解和弹性力学解相差不多,且模型上下应力趋势接近,较为对称,理论解有效;FLAC3D计算的数值解为19.98 MPa。matlab计算两种力学解误差如下:弹性力学解理论值为23.03 MPa,误差为15.2%;材料力学解理论值为23.09 MPa,误差为15.6%。分析图4,在模型x = 15 m时,弹性力学解更为接近。FLAC3D计算的数值解为8.85 MPa,matlab计算两种力学解误差如下:弹性力学解理论值为9.85 MPa,误差为11.3%;材料力学解理论值为10.03 MPa,误差为13.1%,综合上面两个位置正应力曲线图,弹性力学解更加精确些。
分析图5得出两钟力学解与数值解十分接近,在x = 15 m处时,数值解的最高点,即最大切应力为0.94 Mpa,弹性力学解理论值和材料力学解理论值均一样,最大切应力为0.93 MPa,误差为1.1%,符合实际工程精度。
2) 当h/l = 0.2时,取h = 8, L = 40
取边缘x = 0处节点和x = 15 m处节点为考察点,通过弹性力学解和材料力学解得到不同高跨比条件下的正应力解和剪应力解见图6~8。
分析图6,当在支座处x = 0的时候,可看出模型上下应力趋势接近,且较为对称。其中弹性力学解和材料力学解都较为接近数值解,说明两种力学解可行;FLAC3D计算的数值解为10.45 MPa,matlab计算两种力学解误差如下:弹性力学解理论值为12.59 MPa,误差为20.4%;材料力学解理论值为7.25 MPa,误差为30%。对比图7,在模型x = 15 m时,可看出模型上下应力趋势接近,且较为对称。其中弹性力学解和材料力学解都较为接近数值解。FLAC3D计算的数值解为3.42 MPa,matlab计算两种力学解误差如下:弹性力学解理论值为4.11 MPa,误差为20.1%;材料力学解理论值为2.51 MPa,误差为26.3%。
分析图8得出两钟力学解与数值解十分接近,在x = 15m处时,数值解的最高点,即最大切应力为0.49 Mpa,两种力学理论解均一样,最大切应力为0.46 MPa,误差为6.1%,符合实际工程精度。
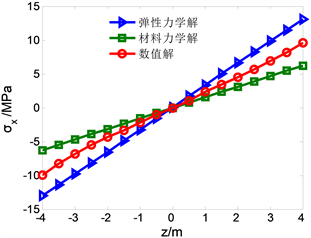
Figure 6. Change with z when x = 0 m
图6. x = 0 m时,
随z的变化
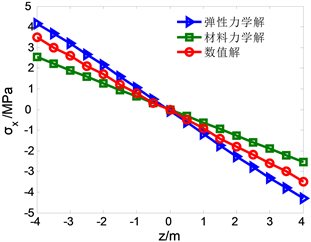
Figure 7. Change with z when x = 15 m
图7. x = 15 m时,
随z的变化
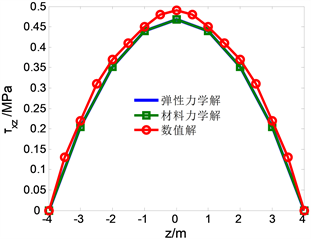
Figure 8. Change with z when x = 15 m
图8. x = 15 m时,
随z的变化
3) 当h/l = 0.3时,取h = 12, L = 40
取边缘x = 0处节点和x = 15 m处节点为考察点,通过弹性力学解和材料力学解得到不同高跨比条件下的正应力解和剪应力解见图9~11。
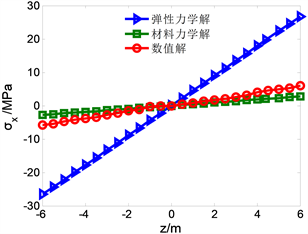
Figure 9. Change with z when x = 0 m
图9. x = 0 m时,
随z的变化

Figure 10. Change with z when x = 15 m
图10. x = 15 m时,
随z的变化
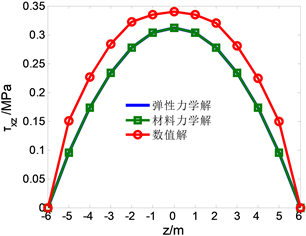
Figure 11. Change with z when x = 15 m
图11. x = 15 m时,
随z的变化
分析图9,当在支座处x = 0的时候,可看出模型上下应力趋势接近,且较为对称,材料力学解更为接近,理论解有效。且上下应力大部分呈对称分布;FLAC3D计算的数值解为5.99 MPa,matlab计算两种力学解误差如下:弹性力学解理论值为28 MPa,误差较大;材料力学解理论值为3.09 MPa,误差为48%。对比图10,在模型中间位置即x = 15 m时,可看出模型上下应力趋势接近,且较为对称。弹性力学解和材料力学解与数值解开始误差加大。FLAC3D计算的数值解为11.8 MPa,matlab计算两种力学解误差如下:弹性力学解理论值为23.1 MPa,误差相对较大;材料力学解理论值为2.12 MPa,误差为82%。
分析图11得出两钟力学解与数值解十分接近,在x = 15 m处时,数值解的最高点,即最大切应力为0.345 Mpa,弹性力学解理论值和材料力学解理论值均一样,最大切应力为0.313 MPa,误差为9.2%,符合实际工程精度。
4) 当h/l = 0.4时,取h = 16, L = 40
取边缘x = 0处节点和x = 15 m处节点为考察点,通过弹性力学解和材料力学解得到不同高跨比条件下的正应力解和剪应力解见图12~14。
分析图12,当在支座处x = 0的时候,可看出模型上下应力趋势接近,且较为对称,材料力学解更为接近数值解,弹性力学的误差相对较大;FLAC3D计算的数值解为6.18 MPa,matlab计算两种力学解误差如下:弹性力学解理论值为58.1 MPa,误差越来越大;材料力学解理论值为1.09 MPa,误差为78.9%。对比图13,在中点处x = 15 m时,弹性力学解误差相对较大,材料力学解虽较为接近但也超出了误差范围。FLAC3D计算的数值解为13.85MPa。matlab计算两种力学解误差如下:弹性力学解理论值为58.56MPa,误差比较大;材料力学解理论值为2.32 MPa,误差为83.2%。
分析图14得出两钟力学解与数值解十分接近,在x = 15m处时,数值解的最高点,即最大切应力为0.26 Mpa,两种力学理论解均一样,最大切应力为0.23 MPa,误差为11.5%,符合实际工程精度。

Figure 12. Change with z when x = 0 m
图12. x = 0 m时,
随z的变化
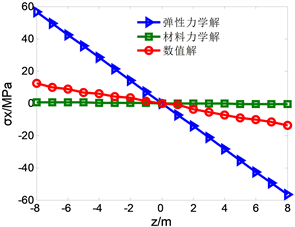
Figure 13. Change with z when x = 15 m
图13. x = 15 m时,
随z的变化
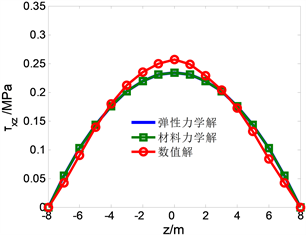
Figure 14. Change with z when x = 15 m
图14. x = 15 m时,
随z的变化
取边缘x = 0处节点和x = 15 m进行应力分析,得到不同高跨比条件下的正应力解和剪应力解见表1、表2。

Table 1. Comparative analysis of tensile stress of two mechanical solutions under different height-span ratios
表1. 不同高跨比条件下两种力学解的拉应力对比分析

Table 2. Comparative analysis of elastic and material mechanical shear stress solutions under different height-span ratios
表2. 不同高跨比条件下弹性力学解与材料力学解剪应力对比分析
从表1正应力对比分析可以看出,高跨比为0.1时,弹性力学解的最大误差为15.2%,材料力学解最大误差为15.6%,弹性力学略微精确。当达到临界值0.2时,材料力学解最大误差达到30%,与弹性力学解的误差在10%左右。当高跨比超过0.2时,弹性力学解误差出现陡增,材料力学解误差也在逐渐增大,浅梁理论不在适用。
从表2剪应力对比分析,由于两者公式相同,故解析解值一样。在高跨比0.1~0.4中。剪切应力解与数值解的最大误差不超过11.5%,符合精度要求。
通过对比不同高跨比下两力学解的应力和数值分析,发现当跨比不超过0.2时,弹性力学解较为精确,高跨比超过0.2时,两者浅梁理论不在适用关键层应力分析运用。
5. 结论
1) 数值计算表明,当h/l ≤ 0.2时,弹性力学解和数值解相差不大,在实际误差范围内。虽然在理论分析中材料力学对于杆件受力分析的方法在工程误差范围内,但弹性力学解略微精确,建议首选采用弹性力学解对隔水关键层进行受力分析.超过0.2时,两者浅梁理论不在适用隔水关键层。
2) 当将水压力近似看场均布荷载施加在关键层的时候,可以近似看出两端固定力学模型;由于均布荷载下固定梁的特点,下部受拉应力影响,而岩石抗拉强度一般较小,底板容易因开采扰动引起的应力重分布导致突水发生,故关键层的端部最底部的位置是防治底板突水的关键部位。而在x = 15 m处,靠近中层位置,弹性力学解浅梁解误差在11.3%相比材料力学解13.1%更为精确。在端点X = 0处两者误差相差不多,为0.4%。
3) 综合考虑
和
随着x、z的变化以及两种算法的精确程度,当高跨比不超过0.2时,弹性力学解应对浅梁分析更为贴切工程实际,且计算较为精确,在实际工程运用中,对于关键层的位移以及受力的内部应力变化有较好的理论支撑,可为底板突水的预测预报情况起到较好的指导作用。
基金项目
安徽省教育厅2019年高校自然科学研究重大项目(KJ2019ZD11);国家自然科学基金面上项目(No. 41977253)。
参考文献