基于时间序列模型的货币供应量预测

Forecast of Money Supply Based on Time Series Model

摘要: 货币供给是重要的金融变量和重要的宏观经济变量，对稳定宏观经济运行以及金融市场起着不可忽视的作用。本文对2010年1月~2020年4月的货币供应量月度数据拟合SARIMA(2,1,1)(1,0,0)12模型，并预测2020年5~9月的数据，将预测值与实际观察值进行对比。根据SARIMA(2,1,1)(1,0,0)12拟合结果发现，第一，我国广义货币供应量变动规律主要受上两期货币供给的影响和上一期货币供给随机干扰的影响。第二，2020年5月~9月份数据的平均相对误差为0.228%，说明模型的预测效果良好。第三，选择的模型不仅能很好地拟合序列趋势，对未来长期货币供应量的预测也有很好的借鉴意义。

Abstract: Money supply is an important financial variable and an important macroeconomic variable, which plays an important role in stabilizing macroeconomic operation and financial market. In this paper, the monthly data of money supply from January 2010 to April 2020 is fitted with SARIMA(2,1,1)(1,0,0)12 model, and the data from May to September 2020 are predicted. The predicted value is compared with the actual observed value. According to SARIMA(2,1,1)(1,0,0)12 fitting results, it is found that, firstly, the change law of broad money supply in China is mainly affected by the last two periods of money supply and the random interference of the last period of money supply. Second, the average relative error of the data from May to September in 2020 is 0.228%, which shows that the prediction effect of the model is good. Third, the selected model can not only fit the trend of the series well, but also provide a good reference for the prediction of the future long-term money supply.

1. 引言

国际金融危机爆发以来，全球性信贷紧缩，各国中央银行因此实施更加宽松的货币政策，加大信贷资金，但也于事无补。经济学家对此的解释之一为货币供应量的错误发行。货币当局实施长期持续的宽松的货币政策，以高收益报酬率刺激投资，通过次贷证券化来提高资产流动性，贷款公司为了高收益推波助澜，相互推动泡沫扩大，结果导致越来越多资金进入虚拟经济，与实体经济增长不相适应，而美国陷入一个债务链，最终促使了金融危机的爆发。为了减缓此次金融危机对我国经济造成的影响，我国政府同样颁布了宽松的货币政策和财政政策，以解决沉重的国际债务问题。

在中国，狭义的货币供应量(M1)的流动性较强，而M2是货币存量的总体，包括流动性较强的货币和流动性较低的存款总额，M2的可控性、可测性较强。80年代以来，很多学者对M1进行预测，随着中国金融市场和房地产市场的快速发展，中国经济的组成成分、结构、形态越来越多样化，对M1的预测日益不能满足中国经济发展需要，目前更多学者关注于对广义货币供应量(M2)的预测，使用M2作为我国货币政策的中介目标。那么货币供应量的长期趋势是怎么样的？应该如何预测短期中的货币供应量呢？如何选择最优预测模型呢？

2. 文献综述

目前对于货币供给量的主要预测方法有灰色预测、建立自回归移动平均(ARIMA)模型、传统回归模型以及向量自回归(VAR)模型。自回归移动平均模型常用于金融时间序列数据的分析预测中，是一种预测精度较高的短期预测方法。大多数学者在预测货币供给量的走势上都运用到ARIMA模型。孙亚星、徐庭兰(2009) [1] 利用ARIMA模型对我国2000年1月~2009年4月实际货币供应量数据进行定量研究，并预测了往后十个月的货币供应量走势，结果显示模型的预测精度和稳定性都较高。刘畅(2011) [2] 以时间的多项式为因变量建立回归模型，采用ARIMA对回归模型进行调整发现，货币当局以前两个月的货币供应量为参考标准制定货币发行量。刘宝宁、张辉(2014) [3] 利用ARIMA模型对我国2013年的货币供应量作出预测，发现预测结果与实际值的平均相对误差仅有1.1%。

一些学者在ARIMA模型的基础上添加了季节性因素和方差因素，陈雄强、张晓峒(2011) [4] 设定虚拟变量来克服货币供应量的交易日效应，采用加权的方法克服移动假日效应，对货币供应序列建立X-13ARIMA模型进行了季节调整分析，并说明环比数据比同比数据更能发现经济指标的转折点。雷祥善(2015) [5] 认为货币供给量序列存在季节性，利用SARIMA分析了货币供应量的变动规律并根据该模型预测变量未来的走势。董晓羿、申世昌(2019) [6] 发现2005年1月到2019年2月的广义货币供应量数据具有异方差性，选择拟合EGARCH(1,1)模型对数据进行分析。谈星(2020) [7] 通过残差检验、样本内外的比较选择拟合SARIMA(2,1,1) × (0,1,1)模型。胡成雨等(2020) [8] 对货币供给数据建立SARIMA模型并引入“剪刀差”的概念探讨广义货币供给增速与狭义货币供给增速的关系。

为了考虑其他宏观变量对货币供给的影响，周天(2009) [9] 以1978~2006年的实际狭义货币供给序列为被解释变量，以实际国民收入为解释变量建立传统回归模型，并且与ARIMA模型的预测精度作对比，发现传统回归模型具有更精确的短期预测精度。胡俊华(2010) [10] 从金融市场上选取三个会影响我国货币供给量的宏观因素，建立多变量回归模型说明可通过观察金融市场中宏观重要变量的变化来预测货币供给的变化。刘顺飞，谢圣远(2017) [11] 对国内生产总值(GDP)、货币供应量、准货币供应量建立VAR模型，发现从短期来看，GDP会影响到货币供应量和准货币供应量的预测，而长期来看，GDP只能影响到准货币供应量的预测。

近些年，灰色预测方法也被用来预测货币供给量，丁少玲、江鹏辉(2019) [12] 通过GM(1,1)灰色预测模型预测2018~2020年我国货币发行量，但模型相对误差序列未达到预期精度。龚旭云、蒋祝仙(2020) [13] 使用GM(1,1)灰色预测模型预测货币的构成成分，然后使用Divisia货币指数来加总货币，并使用M2占GDP的比例检验了预测数据的可靠性。

少数学者在选择变量、测度方法上与原来的传统方法有所不同。池启水、王振全(2015) [14] 运用计量经济学的断点检验分析历史上重大离散事件对货币供应量的影响。王洪平(2020) [15] 运用支持向量机(SVM)来反映货币供应量与金融机构贷款之间的复杂非线性关系，取得了较好的预测效果。

综上所述，建立回归模型和VAR模型预测货币供给量的缺陷在于模型无法将货币供给的影响因素完全考虑进去，如果仅仅使用几个主要因素判断未来货币供给量，会由于考虑不全面而低估了货币供给。而灰色预测模型虽然对样本要求不高，但预测结果有很大误差，因此本文选择对2010年1月~2020年4月的货币供应量月度数据拟合恰当的SARIMA模型，并预测2020年5~9月的数据，将预测值与实际观察值进行对比，根据模型的AIC值与平均相对误差来选择最优的SARIMA模型。

3. 理论模型

3.1. 单位根检验

建立ARMA模型之前，一个必要步骤是对序列进行平稳性检验。一般可以根据时序图和自相关图来判断序列的平稳性，此外也可以运用单位根检验的结果来判断序列是否平稳，而ADF检验在实践中最为常用的。ADF检验包括三种模型，分别为无常数项无趋势项、有常数项无趋势项、无常数项无趋势项的模型：

$\Delta x_t=\delta x_{t-1}+{\displaystyle {\sum }_{i=1}^m{\beta }_i\Delta x_{t-i}+{\epsilon }_t}$ (1)

$\Delta x_t=\alpha +\delta x_{t-1}+{\displaystyle {\sum }_{i=1}^m{\beta }_i\Delta x_{t-i}+{\epsilon }_t}$ (2)

$\Delta x_t=\alpha +\beta t+\delta x_{t-1}+{\displaystyle {\sum }_{i=1}^m{\beta }_i\Delta x_{t-i}+{\epsilon }_t}$ (3)

检验的原假设为序列存在值为1的单位根，也可将其表示为 $H_0$ ： $\delta =0$，原序列平稳的条件就是ADF检验的统计值小于临界值，或其对应的P值小于显著性水平，否则就将原序列视为非平稳。检验模型的选择具体看序列时序图是否有截距项和趋势性，模型阶数的选择一般从高阶到低阶，直到模型最后一阶的参数显著为止。上述模型中若m = 0，则为DF检验，DF检验是ADF检验的简单模式。如果进行检验后，结果显示序列不平稳，则需对原序列作差分处理，使其成为平稳序列。

3.2. 自回归移动平均(ARIMA)

Box、Jenkins在1976年最早提出了ARIMA模型，它是对ARMA模型的一个扩展。如果一个时间序列不平稳，对差分平稳后的序列建立的ARMA模型即为ARIMA模型，可记为ARIMA(p,d,q)。其中，d表示差分阶数，它使得原序列在d阶差分后变得平稳；p和q分别表示自回归和移动平均的阶数。ARIMA模型的具体形式为：

$\left(1-{\displaystyle {\sum }_{i=1}^p{\phi }_i{B}^i}\right){\left(1-B\right)}^d{X}_t=\left(1+{\displaystyle {\sum }_{i=1}^q{\theta }_i{B}^i}\right){\epsilon }_t$ (4)

其中， $x_t$ 是原始序列， ${\epsilon }_t$ 是白噪声序列，B是滞后算子。

3.3. 季节性差分自回归移动平均(SARIMA)

ARIMA模型通过对序列差分提取序列的趋势性，但有时候序列不仅仅只包含趋势特征，很多金融时间序列还呈现出一定的周期性和季节性，此时ARIMA模型不能很好地拟合有周期性特征的序列，而SARIMA模型通过将序列进行S步差分提取出序列的周期性特征，S即为序列的周期。如果原序列同时存在趋势和周期波动，则可表示为SARIMA(p,d,q)(P,D,Q)^s模型，其中d为逐期差分的阶数，p、q分别为自回归和移动平均的阶数；D则代表季节差分的阶数，P、Q分别表示在季节上的自回归和移动平均阶数，模型可表示为：

${\phi }_p\left(B\right){\Phi }_p\left(B^S\right){\left(1-B\right)}^d{\left(1-B^S\right)}^D{X}_t={\theta }_q\left(B\right){\Theta }_Q\left(B^S\right){\epsilon }_t$ (5)

其中， ${\left(1-B^S\right)}^D$ 表示季节性差分。

3.4. 建模思想

3.4.1. 建模步骤

建立ARIMA和SARIMA模型时，第一步是对序列的平稳性检验，若序列不平稳则需要差分处理，直至序列平稳后才可以对差分序列建立模型。第二，对序列进行随机性检验，假如序列检验为白噪声，则停止对序列建立模型，因为序列当中已经没有可以提取的信息，假如序列检验为非白噪声，再进行下一步。第三，模型的识别与定阶。根据差分后平稳序列的自相关和偏自相关图的拖尾和截尾特征，可以判断能够尝试拟合何种ARMA模型。第四，模型诊断检验，该步骤是通过检验所建立模型的残差序列是否纯随机，以此来判断模型是否是显著的。除此之外，根据模型的特征根也可以检验其平稳性。第五，在模型定阶过程中，会选择多个适合的模型进行拟合，比较多个模型的AIC和SC值，最小的即为最优模型。

3.4.2. 预测和预测评价

对于模型的预测效果，学者一般选择一个历史时间点，对该时间点之前的历史数据建立模型，然后利用模型对该时间点之后的历史数据进行预测，比较计算实际值和预测值的差别。有以下两个指标可以比较实际值和预测值的差别：

1) 平均相对误差绝对值

$MAPE=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n\left|\frac{x_t-{\hat{x}}_t}{x_t}\right|}$ (6)

2) Thiel不相等系数

$U=\frac{\sqrt{\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left({\hat{x}}_t-x_t\right)}^2}}}{\sqrt{\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left({\hat{x}}_t\right)}^2}}+\sqrt{\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{\left(x_t\right)}^2}}}$ (7)

如果平均相对误差较小，U值接近于0，那么预测模型效果是较好的。

4. 数据来源和处理

随着中国经济的组成成分、结构、形态越来越多样化，至2007年以后正式只提广义货币供应量M2增长目标。因此本文选择广义货币供应量M2作为分析对象。考虑到2010年以前的数据年代太久远，不具有预测意义，因此选择时间区间为2010年至2020年的月度数据，其中2020年5月至9月的数据用于检验模型的预测能力，其他数据(共124个样本)用于模型建模。数据全部来源于东方财富网。

5. 实证分析

5.1. 数据特征检验

将数据导入R软件，绘制2010年1月~2020年4月的中国货币供应量(M2)的时序图，如图1所示，M2序列的时序图呈逐步上升趋势，需要对该序列进行差分处理以消除上升趋势。

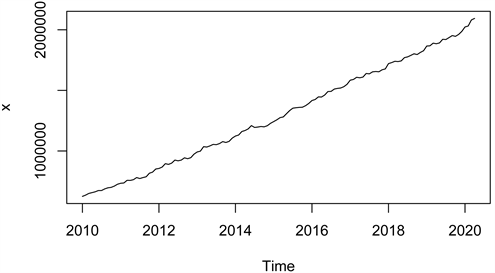
Figure 1. Curve: China’s money supply from January 2010 to April 2020

图1. 2010年1月~2020年4月的中国货币供应量时序图

对该序列做一阶差分，绘制出一阶差分后的序列时序图如图2，图2显示序列无明显的趋势，在一条水平线上上下波动，可认为一阶差分序列是平稳的。

对序列采用ADF单位根检验来进一步对序列平稳性做出判断，首先选择有趋势项、有截距项的模型三作为检验模型，检验结果显示模型的趋势性和截距项均显著不为0，因此将模型三作为检验模型是合理的。ADF统计量为−8.5951，查表得5%的显著性水平下临界值为−3.43，差分后的序列有95%的概率是平稳的。

接着对差分后序列进行白噪声检验(表1)，取显著性水平为5%，延迟6阶和12阶的LB统计量P值均显著小于5%，序列有95%的概率为白噪声，一阶差分后的货币供应量序列不是纯随机的，序列当中还有未提取完全的信息，需继续拟合模型。

Figure 2. Curve: The first-order difference of China’s money supply from January 2010 to April 2020

图2. 2010年1月~2020年4月的中国货币供应量一阶差分时序图

Table 1. White noise test of first-order difference Chinese money supply series

表1. 一阶差分中国货币供应量序列白噪声检验

5.2. 模型选择和优化

观察货币供给量平稳后序列的自相关图和偏自相关图(图3)来进行模型的定阶，发现序列的自相关函数在每个阶数为12阶的周期上均显著，说明序列有阶数为12阶的周期性，这对于月度数据来说是很常见的，考虑对数据进行12步差分提取序列的周期性，并进行纯随机检验，发现季节差分后序列通过了纯随机的检验，季节差分后序列为白噪声，不能继续拟合模型。本文的做法是不对原始序列进行季节差分，但是拟合季节系数，即拟合SARIMA(p,1,q)(P,0,Q)模型。

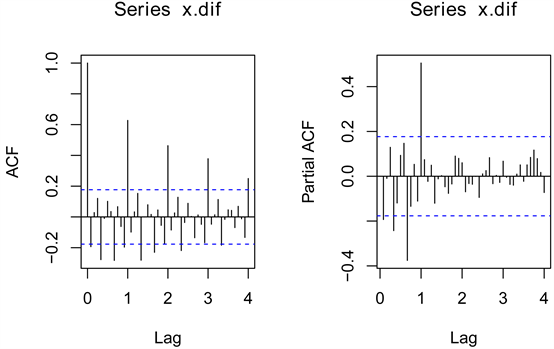
Figure 3. Autocorrelation and partial correlation diagrams of China’s money supply based on first-order difference

图3. 一阶差分的中国货币供应量自相关、偏相关图

由自相关图可看出自相关系数周期上拖尾，周期内也拖尾，偏自相关系数周期上2阶截尾，周期内拖尾，因此可选择P = 2，Q = 0，而p、q的选择从低阶的(1,1)开始，逐渐升阶，对比各个模型系数显著性、模型显著性以及AIC，选择最优模型。在拟合模型时发现若P = 2模型中SAR(2)系数均不显著，因此选择P = 1，最终可供选择的模型有SARIMA(1,1,1)(1,0,0)₁₂、SARIMA(2,1,1)(1,0,0)₁₂、SARIMA(1,1,2)(1,0,0)₁₂、SARIMA(2,1,2)(1,0,0)₁₂模型。

每个模型对应的显著性和AIC值如下表2：

Table 2. Saliency and AIC value corresponding to the model

表2. 模型对应的显著性和AIC值

选择模型显著、参数也通过显著性检验中AIC值最小的模型即SARIMA(2,1,1)(1,0,0)₁₂模型为最优模型。

5.3. 参数估计

SARIMA(2,1,1)(1,0,0)₁₂模型参数拟合结果如表3。在10%的显著性水平下，各参数都通过显著性检验。

Table 3. SARIMA(2,1,1)(1,0,0)12 model parameter estimation

表3. SARIMA(2,1,1)(1,0,0)₁₂模型参数估计

模型展开式可写成：

$\left(1-0.8452B-0.1538B^2\right)\left(1-0.7046B^{12}\right)\left(1-B\right)X_t=\left(1-0.9789\right){\epsilon }_t$ (8)

5.4. 模型检验

对拟合模型的残差进行白噪声检验，若残差序列为白噪声，说明模型整体显著，否则，序列中还存在未提取完整的信息，模型不显著。残差白噪声检验结果如表4，计算序列延迟6期之前的LB统计量，取显著性水平为5%，延迟1~6阶LB统计量P值均高于5%，残差序列有95%的概率为白噪声，对货币供给量拟合SARIMA(2,1,1)(1,0,0)₁₂模型是合适的。

5.5. 预测

利用上述得到AIC最小的SARIMA(2,1,1)(1,0,0)₁₂模型预测2020年5月~9月的货币供应量拟合预测，将预测值与实际值之差除以实际值，计算相对误差，得到表5。

Table 4. SARIMA(2,1,1)(1,0,0)12 Residual white noise test

表4. SARIMA(2,1,1)(1,0,0)₁₂模型残差白噪声检验

Table 5. Forecast result of money supply

表5. 货币供应量预测结果

预测值与实际值的走势对比如图4。

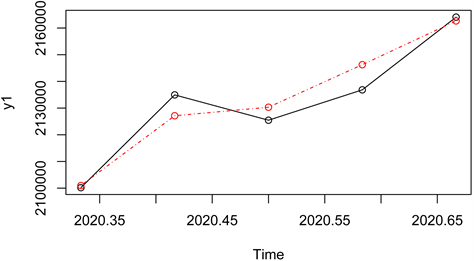
Figure 4. Comparison of model prediction results

图4. 模型预测结果对比

由上表和上图可以看出，SARIMA(2,1,1)(1,0,0)₁₂模型拟合2020年5月~9月份数据的误差百分比都很小，都小于1%，计算得到平均相对误差为0.228%，预测精度均达99.5%以上，说明模型的预测效果良好。一般SARIMA模型都只能预测短期数据，在本例子中，对于滞后5期的预测误差仅为0.065%，预测精度甚至高于前三期的精度，进一步说明选择的模型不仅能很好地拟合序列趋势，对未来货币供应量的预测也有很好的借鉴意义。

6. 结论

货币供给量发行不足会导致供不应求，制约我国的经济发展，发行过多则会导致通货膨胀的发生，也不利于经济的稳定发展，因此正确地预测适度的货币供应量是货币政策的关键。中央银行通过调节货币供应量的变化来调控社会经济发展，研究货币供应量的变化对国家宏观经济管理部门有着重要的建设意义。本文选择广义货币供应量M2作为分析对象。因此选择时间区间为2010年至2020年的月度数据，其中2020年5月至9月的数据用于检验模型的预测能力，其他数据(共124个样本)用于模型建模。

本文中使用的数据(广义货币供应量M2)是非平稳的，通过一阶差分后变得平稳。在对一阶差分序列进行12步差分后进行纯随机检验，发现季节差分后序列通过了纯随机的检验，季节差分后序列为白噪声，因此不对原始序列进行季节差分，但是拟合季节系数。最终拟合SARIMA(2,1,1)(1,0,0)₁₂模型作为最终预测模型。根据SARIMA(2,1,1)(1,0,0)₁₂拟合结果发现，第一，我国货币当局以前两个月的广义货币供应量为参考标准，还将上一期的随机干扰考虑进去，以此制定广义货币发行量。第二，2020年5月~9月份数据的误差百分比都很小，都小于1%，计算得到平均相对误差为0.228%，预测精度均达99.5%以上，说明模型的预测效果良好。第三，一般SARIMA模型都只能预测短期数据，在本例子中，对于滞后5期的预测误差仅为0.065%，预测精度甚至高于前三期的精度，进一步说明选择的模型不仅能很好地拟合序列趋势，对未来货币供应量的预测也有很好的借鉴意义。