1. 引言
对考试结果进行进一步分析,不仅有助于教师了解学生们对其所授知识点的掌握情况,还将有益于教师检验、完善自己的教学方法,提升自己的教学技能,从而使得紧密相连的“教”与“学”相互启发、相互促进、相互补充。近年来已有众多研究者从不同角度对此展开了讨论和研究。
2005年连德忠 [1] 通过编译MATLAB程序,基于难度系数 = 1 − 该题平均得分值/该题满分值,区分度 = (高分组该题平均得分值 − 低分组该题平均得分值)/该题满分值,实现了成绩统计和考试质量分析。2018年吴楠等人 [2] 提出了一种基于试卷难度系数变化的修正模型,实践证明该修正模型可以提升预测精度、减少误差。2019年陈志江 [3] 结合“大数据”下积累的数学教研分析资料,示范如何以教研指导教学,形成了区域教研特色。2020年薛井杰和冰洁 [4] 在设定和修改试题各组成要素的过程中,通过试题结构模型和难度系数的界定标准真正实现对试题难度系数的把控。2020年唐莹莹 [5] 基于统计分析工具SPSS和合肥工业大学2019年春季学期二级大学英语期末考试的成绩数据,探讨了考试难度、信度、各类型题型成绩的相关性以及不同学生群体成绩的差异性,进一步验证了考试的效度。张团笑等人 [6] 使用SPSS统计软件包和Excel对川北医学院临床医学专业2005~2009级4886名本科生的生理学考试成绩进行数据处理和统计分析,发现学生的生理学成绩从年级角度来看无明显差异,但从男女性别来看却存在较大的差异。段宝军等人 [7] 运用SPSS对河西学院随机抽取的8个系16门考试课成绩进行统计分析,结果表明不同的大类学科与难度系数等级以及区分度系数等级之间的卡方检验没有显著的统计学意义。最近,杨君和陈志国 [8] 对等级性考试的等级赋分方案和相应的区分要求、等级成绩的呈现方式和使用以及相应考生成绩分布和难度结构展开了深入的研究。边迅 [9] 尝试在教学过程加入“学子出单元卷”的新考核方式,活跃了学生的思维,加深了学生对知识的理解,并加强了学生之间的团队协作能力,不过作者也对该考核方式存在的问题提出了改进措施。此外,基于AHP理论、SPSS等分析工具对试卷质量展开分析和评价的相关文献还有很多,读者可以参见 [10] - [17]。
本文基于扬州大学数学科学学院2021年春季学期数学1902~1905四个班级153人(含1名重修生和1名休学班的同学)的《概率论与数理统计》课程考试成绩数据,运用统计学中方差分析理论和MATLAB工具,对此次考试成绩进行了详细的分析和探讨。
2. 考试及课程目标达成度分析
2.1. 考试基本情况
基于扬州大学数学与应用数学专业课程教学大纲(2019版) [18],笔者设计了对应课程目标的考核试题,具体课程目标详见附录,基本题型和分值详见表1。

Table 1. Correspondence table of course objectives and final examination papers
表1. 课程目标与期末试卷对应表
本次试卷综合考察了Bayes公式的应用、随机变量的分布函数、随机变量的数字特征、二维随机变量的边际密度、联合分布函数、密度函数等、分布函数的极限(极限分布)、多项分布的边际分布的证明以及中心极限定理和大数定律的综合证明等。考试题型为判断题(10分)、选择题(15分)、计算题(60分)、证明题(15分)。数学1902~1903班级(合班上课)实际平均得分为:判断题(6分)、选择题(8.79分)、计算题(28.11分)、证明题(5.83分);数学1904~1905班级(合班上课)实际平均得分为:判断题(5.65分)、选择题(10.04分)、计算题(35.86分)、证明题(8.14分)。
· 从监考时观察学生用时来看,试卷题量适中;
· 从阅卷后学生的高分分布来看,难度略微偏难,但总体成绩还是服从正态分布(详见图1);

Figure 1. Frequency histogram and theoretical normal distribution function
图1. 频率直方图和理论正态分布函数
· 从卷面的题型以及综合客观题和主观题的因素看,数学1902~1905学生掌握情况较为平均,数学1902~1903的判断题和选择题的得分率在60%,计算题的得分率不到50%,证明题的得分率在40%;数学1904~1905的判断题和选择题的得分率在63%,计算题的得分率不到60%,证明题的得分率在54%;
· 从卷面考核的具体内容看,数学1902~1905的同学们对分布函数的应用掌握的均较差,对中心极限定理和大数定律的基本概念掌握的均较好,但是数学1902~1903对于如何通过中心极限定理(非契比雪夫不等式)证明贝努利大数定律掌握的较差,而数学1904~1905对此知识点掌握的程度稍好。
2.2. 平时学习分析
平时成绩主要分为出勤(10分)、课堂表现(15分)、平时作业(20分)、平时测验(40分)、反思总结(15分),四个班级部分同学虽然在平时随堂测验表现有些差强人意,但同学们平时学习表现积极,课堂上能够和教师探讨解题的类型和方式,作业情况也完成的很好,总体来说非常不错。数学1904~1905在具有突击检查性质的平时随堂测验却表现出了比平行班级数学1902~1903更好的成绩,平时学习课堂表现积极,作业情况也完成的很好,总体来说非常不错。
2.3. 总成绩分析
鉴于卷面得分率不是很高,课程总成绩的构成按照期末成绩占比60%,平时成绩占比40%计算。数学1902~1903的均分66.2分,最高分86分,最低分12分,补考16人(含重修和休学班2人)占班级总人数的22.22%,60~79分的学生数约占班级总人数的68.06%,80分以上的学生占到班级总人数的9.72%。数学1904~1905均分74分,最高分92分,最低分51分,补考4人占班级总人数的4.94%,60~79分的学生数约占班级总人数的65.43%,80分以上的学生占到班级总人数的29.63%。笔者第十个年度教授《概率论与数理统计》这门课程,由于所授班级的每年录取成绩、专业、班级学风等诸多因素的影响,在教学方法和技能上虽无法同笔者往年教授的其他班级直接比较,但同笔者同学期教授的平行班级数学1904~1905相比,数学1902~1903的补考人数占到了总补考人数的75%,正好为数学1904~1905补考人数的4倍,数学1904~1905的补考人数仅占总补考人数的25%,尤其是数学1905班表现出色,没有同学补考。此外,如图2和图3所示,数学1904~1905在正态性上以及箱线图中的表现也比数学1902~1903要更胜一筹。
此外,在显著性水平0.05下,笔者通过方差齐性检验发现检验的p值p = 0.4893 > 0.05,说明四个班级的学生成绩服从方差相同的正态分布,也就是满足方差分析的基本假定,具体结果详见表2。

Figure 2. The experience distribution of the scores of mathematics classes 1902~1905
图2. 数学1902~1905班级总成绩的经验分布
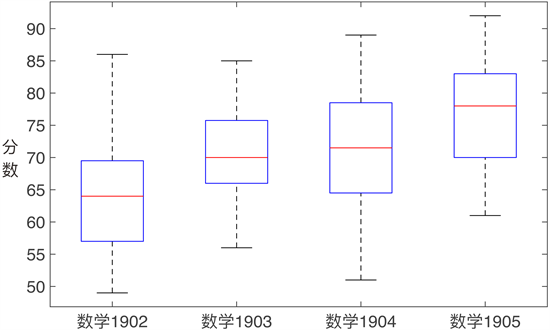
Figure 3. Box diagram for the course examination of mathematics classes 1902~1905
图3. 数学1902~1905班级课程考试的箱线图

Table 2. Analysis of variance results for four classes
表2. 四个班级的方差分析结果
3. 存在问题分析
从卷面和总成绩看,笔者认为数学1902~1903学生主要在概率论知识的应用方面存在较大困难,比如期末考试关于求陀螺的分布函数的题目,其原理和所授学期的随堂测试内容以及2021年考研数学二的最后一题相同,但得分率依然很低;同时,同学们在计算方面的出错也略多,比如关于协方差和相关系数的计算的得分率也较低。除此之外,近十年来的教学让笔者感受到很多的同学背负的学习压力较大,对于分数的在意程度和渴求超越了常态,在随堂测验和期末考试之后部分同学会为了自己的分数联系教师“要分”,存有分数是可以“要到”而不是“考出来”的错误观念。在课程教学中,学生们倒没有展现不好之处,反而体现出热爱学习、讨论问题的健康画面。数学1904~1905学生在概率论知识的应用方面也存在一定的理解困难,还有贝努利大数定律的另类证明理解的还不够透彻。在课下,数学1904~1905的同学和教师互动很好,在课程教学中,课堂气氛也较好,但相比平行班级数学1902~1903,学生缺少平时主动讨论问题的习惯,考前几天却爆发性地咨询问题。通过和同学们的实际沟通,笔者发现数学1905多是转专业的学生,为了不挂科或者“赶上”原先数学专业的学生,大家学习的主观能动性非常强,相反数学1902的少数同学抱有大一是高分被录进来的心理“优势”,不是非常重视中学阶段就接触到的概率论,结果被其他班级极速反超。

Table 3. Achievement of the teaching goals of mathematics classes 1902~1903
表3. 数学1902~1903班级的教学目标达成情况

Table 4. Achievement of the teaching goals of mathematics classes 1904~1905
表4. 数学1904~1905班级的教学目标达成情况
4. 进一步思考与改进措施
考虑试题的难度系数后,根据对应课程目标的具体卷面得分,数学1902~1903的本课程目标达成度为82% (如表3所示),数学1904~1905的本课程的目标达成度为83.7% (如表4所示),虽然都不同程度地达到了课程教学目标,然而平时暴露出来的问题却会潜在影响着同学们后续课程的学习以及对低年级的同学可能也会起到不好的引导作用,因此建议具有类似情况的授课教师:
1) 在课程教学中的例题讲解环节,尽量紧扣同学们关心的事件以及时事热点,最大限度地激发同学们的学习热情,比如讲解全概率公式以及事件的加法公式等知识点时可以列举有关新冠肺炎等实例;
2) 在教学中设置更加及时且有效的随堂突击测试环节,从而掌握同学们真实的薄弱环节,有针对性地进行“补缺”教学;
3) 充分利用课下空余时间和同学们进一步交流平时的学习方式和复习方法,根据同学们不同的实际情况给出合适同学们自己学习途径的建议,以避免部分同学考前爆发性地仅仅为了考试而学习、仅仅为了分数而准备考试,或者以各种渠道获取往年试题,结果偏离课堂教学的内容。
基金项目
国家自然科学基金项目(Nos. 12172322, 11672259)、国家留学基金项目(No. 201908320086)和江苏高校品牌专业建设工程资助项目(No. PPZY2015B109)资助。
附录:
《概率论与数理统计》课程的教学目标 [18] 如下:
课程目标1:以概率论与数理统计知识为载体,培养学生树立正确的科学素养,凸显良好的数学品质;通过介绍我国学者成就,进行爱国主义教育、渗透辩证唯物主义思想;通过教师的言传身教,学生能积极践行社会主义核心价值观,坚定从教信念;体会随机的思想方法,感受用随机的方法解决问题的创造性思维,理解随机的数学思想,形成随机与确定相统一的辩证唯物主义观点,完善认识世界的方法;利用案例教学进行道德品质教育,增强师生互动激发学习动力,促进学生思维品质的提升。
课程目标2:通过对概率论与数理统计的学习,理解概率、随机变量、分布函数、数字特征和统计量等概念,学会求概率、分布函数、分布列、密度函数、数字特征和掌握参数估计的方法,提高学生的计算能力,逻辑推理能力,抽象概括能力。
课程目标3:通过对概率论与数理统计课程的研究对象、方法和内容以及学科特点、发展趋势等系统介绍,使学生掌握概率和统计的基本思想、基本理论,提高学生用概率论与数理统计的知识分析和解决实际问题的能力,也为以后进行研究打下坚实的基础。