具有Allee效应和恐惧效应的捕食–食饵系统动力学性质

Dynamic Behavior of a Predator-Prey System with Allee Effect and Fear Effect

摘要: 本文研究一类具有Allee效应和恐惧效应的捕食–食饵模型。我们讨论系统平衡点的存在性，接着分析边界平衡点和正平衡点的稳定性。同时证明系统存在鞍结分支。当Allee效应越强时，越不利于食饵和捕食者种群生存。通过数值模拟，验证系统存在极限环，同时出现双稳现象。增大恐惧效应，会使得正平衡点从不稳定变成稳定，也就是较大的恐惧效应可以促进系统的稳定。

Abstract: This paper studies a predator-prey system with Allee effect and fear effect. We discuss the existence of the equilibria in the system, and analyze the stability of the boundary equilibria and positive equilibria. Also we prove that the system has a saddle-node bifurcation. When the Allee effect is large, it is unfavorable to the survival of prey and predator populations. Through numerical simulation, it is verified that the system has a limit cycle, and show the bistable phenomenon. Increasing the fear effect will make the positive equilibrium from unstable to stable, that is, a larger fear effect can promote the stability of the system.

1. 引言

本文考虑如下具有Allee效应和恐惧效应的捕食–食饵系统：

$\begin{array}{l}\stackrel{\dot{}}{x}=x\left(\frac{ax}{\left(1+ky\right)\left(A+x\right)}-d-bx\right)-mxy,\\ \stackrel{\dot{}}{y}=nmxy-ey,\end{array}$ (1)

其中x和y分别表示食饵和捕食者在t时刻的种群密度，a表示食饵种群的出生率，d和e分别表示食饵和捕食者的死亡率，b表示食饵种群的种群竞争强度，m是捕食者的捕获率，n表示捕食者对食饵的转化

率。参数 $a,A,k,d,b,m,n,e$ 都是正数，并且 $a>d$。定义恐惧效应 $f\left(k,y\right)=\frac{1}{1+ky}$ [1]，其中k表示恐惧的水平。另一方面考虑到Allee效应也会影响食饵种群的出生率，定义 $\frac{ax}{x+A}$ [2] 表示食饵的出生率受到Allee效应的影响，其中 $\frac{x}{x+A}$ 表示食饵的Allee效应，A表示Allee效应的参数。Allee效应的大小取决于参数A，即参数A越大，Allee效应就越强。

在生态系统中，恐惧效应是生态系统中的普遍现象，也就是食饵能感受到被捕食的风险并产生恐惧，同时做出一些相应的改变。所以Wang等学者 [1] 考虑到恐惧效应会影响到食饵种群的出生率，提出如下具有恐惧效应的捕食–食饵模型：

$\begin{array}{l}\stackrel{\dot{}}{u}=u{r}_{0}f\left(k,v\right)-du-a{u}^2-g\left(u\right)v,\\ \stackrel{\dot{}}{v}=v\left(-m+cg\left(u\right)\right),\end{array}$ (2)

其中u和v分别表示食饵和捕食者在t时的种群密度，r₀和d分别表示食饵的出生率和死亡率，a表示食饵种群的种群竞争强度，m表示捕食者的死亡率，c表示捕食者对食饵的转化率， $g\left(u\right)$ 表示功能性反应

函数， $f\left(k,v\right)=\frac{1}{1+kv}$ 表示恐惧效应，k表示恐惧的水平。在文 [1] 中，作者对系统的动力学行为进行了

详细的研究，说明了相对较低的恐惧水平可以通过Hopf分支产生极限环，从而导致双稳现象。最近学者们 [3] [4] [5] 对具有恐惧效应的生态学模型进行了详细的研究，分析系统的动力学性质。

当种群数量较少时，种群的自然增长率是一个负函数或者递减函数，这种现象被称为Allee效应 [6]。近年来，越来越多的野生动物濒临灭绝，Allee效应也引起了广大学者的注意，并得到了广泛的研究 [7] [8]。然而，很少有学者在捕食–食饵模型中，同时考虑出生率都受到Allee效应和恐惧效应的影响。因此，本文提出了系统(1)，并研究系统的动力学性质。

对于系统(1)，为了减少参数的数量，做如下变换

$\begin{array}{l}\bar{x}=\frac{nm}{e}x,\bar{y}=\frac{n{m}^2}{be}y,\bar{t}=\frac{be}{nm}t,\\ \bar{A}=\frac{nm}{e}A,\bar{k}=\frac{eb}{n{m}^2}k,\bar{d}=\frac{nm}{be}d,s=\frac{nm}{b}.\end{array}$

并重新用 $x,y,t,A,k,d$ 分别表示 $\bar{x},\bar{y},\bar{t},\bar{A},\bar{k},\bar{d}$，得到下面的系统

$\begin{array}{l}\stackrel{\dot{}}{x}=x\left(\frac{ax}{\left(1+ky\right)\left(A+x\right)}-d-x\right)-xy,\\ \stackrel{\dot{}}{y}=sy\left(x-1\right),\end{array}$ (3)

其中参数 $a,A,k,d,s$ 都是正数，并且 $a>d$。

为了方便计算，对于系统(3)，作时间变换， $\text{d}t=\left(1+ky\right)\left(A+x\right)\text{d}\tau$ (仍使用t代替 $\tau$ )，得到下述等价系统：

$\begin{array}{l}\stackrel{\dot{}}{x}=x\left[ax-\left(d+x+y\right)\left(1+ky\right)\left(A+x\right)\right],\\ \stackrel{\dot{}}{y}=sy\left(x-1\right)\left(1+ky\right)\left(A+x\right),\end{array}$ (4)

由于拓扑等价的原理，本文将具体分析系统(4)的动力学行为。

2. 平衡点的存在性

显而易见，系统(4)中存在边界平衡点 $E_0\left(0,0\right)$。为了研究系统(4)的其它平衡点，考虑如下方程：

$\{\begin{array}{l}x\left[ax-\left(d+x+y\right)\left(1+ky\right)\left(A+x\right)\right]=0,\\ sy\left(x-1\right)\left(1+ky\right)\left(A+x\right)=0.\end{array}$ (5)

首先，分析边界平衡点的存在性。将 $y=0$ 带入方程(5)的第一个方程，可得：

$x^2+\left(A-a+d\right)x+Ad=0.$ (6)

当 $A-a+d\ge 0$ 时，即 $A\ge a-d$ 时，方程(6)无正根，下面只需要讨论 $A<a-d$ 的情况。记 ${\Delta }_1\left(A\right)={\left(A-a+d\right)}^2-4Ad$，解得 $A_1={\left(\sqrt{a}-\sqrt{d}\right)}^2$ 和 $A_2={\left(\sqrt{a}+\sqrt{d}\right)}^2$。容易得到 $A_1<a-d<A_2$。记 $A^{*}={\left(\sqrt{a}-\sqrt{d}\right)}^2$，所以当 $A^{*}<A<a-d$ 时，有 ${\Delta }_1\left(A\right)<0$。当 $A=A^{*}$ 时，有 ${\Delta }_1\left(A\right)=0$。当 $0<A<A^{*}$ 时，有 ${\Delta }_1\left(A\right)>0$。

综合上述讨论，当 $0<A<A^{\text{*}}$ 时，方程(6)有两个正根，分别记为 $x_1=\frac{a-A-d-\sqrt{{\Delta }_1\left(A\right)}}{2}$， $x_2=\frac{a-A-d+\sqrt{{\Delta }_1\left(A\right)}}{2}$。当 $A=A^{*}$ 时，方程(6)只有一个正根，记为 $x^{\text{*}}=\sqrt{d}\left(\sqrt{a}-\sqrt{d}\right)$。当 $A^{*}<A<a-d$ 时，方程(6)没有实根。所以我们有如下边界平衡点存在的定理。

定理2.1系统(4)的边界平衡点为：

1) 当 $0<A<A^{\text{*}}$ 时，除 $E_0\left(0,0\right)$ 外，系统(4)存在边界平衡点 $E_1\left(x_1,0\right)$ 和 $E_2\left(x_2,0\right)$ ；

2) 当 $A=A^{\text{*}}$ 时，除 $E_0\left(0,0\right)$ 外，系统(4)存在边界平衡点 $E^{*}\left(x^{*},0\right)$ ；

3) 当 $A^{*}<A<a-d$ 时，除 $E_0\left(0,0\right)$ 外，系统(4)不存在边界平衡点。

下面考虑正平衡点的存在性。将 $x=1$ 带入方程(5)的第一个方程中，可得：

$y^2+\left(1+d+\frac{1}{k}\right)y+\frac{1}{k}\left(1+d-\frac{a}{1+A}\right)=0.$ (7)

由于 $1+d+\frac{1}{k}>0$，故当 $1+d-\frac{a}{1+A}<0$ 时，即 $0<A<\frac{a}{1+d}-1$ 时，方程(7)只有唯一的正根 $y_1$。记 ${\Delta }_2\left(A\right)={\left(1+d+\frac{1}{k}\right)}^2-\frac{4}{k}\left(1+d-\frac{a}{1+A}\right)$，则 $y_1=\frac{-\left(1+d+\frac{1}{k}\right)+\sqrt{{\Delta }_2\left(A\right)}}{2}$。

定理2.2当 $0<A<\frac{a}{1+d}-1$ 时，系统(4)存在唯一的正平衡点 $E_3\left(1,y_1\right)$。

3. 平衡点的稳定性

系统(4)在边界平衡点 $\left(x,0\right)$ 处的雅克比矩阵为：

$J\left(x,0\right)=\left(\begin{array}{cc}x\left(a-A-d-2x\right)& -x\left(x+A\right)\left(xk+dk+1\right)\\ 0& -s\left(1-x\right)\left(x+A\right)\end{array}\right),$

并且矩阵 $J\left(x,0\right)$ 的行列式和迹分别为

$\begin{array}{l}\text{Det}\left[J\left(x,0\right)\right]=-sx\left(a-A-d-2x\right)\left(1-x\right)\left(x+A\right),\\ \text{Tr}\left[J\left(x,0\right)\right]=x\left(a-A-d-2x\right)-s\left(1-x\right)\left(x+A\right).\end{array}$

定理3.1系统(4)的边界平衡点 $E_0\left(0,0\right)$ 是稳定的结点。

证明：系统(4)在边界平衡点 $E_0\left(0,0\right)$ 处的雅克比矩阵为

$J\left(E_0\right)=\left(\begin{array}{cc}-Ad& 0\\ 0& -As\end{array}\right),$

特征值 ${\lambda }_1=-Ad<0$ 和 ${\lambda }_2=-As<0$，那么边界平衡点 $E_0\left(0,0\right)$ 是稳定的结点。

定理3.1证明完毕。

注记3.1.当 $d<a\le d+1$ 和 $A>A^{\text{*}}$ 时，容易知道平衡点 $E_0\left(0,0\right)$ 外，不存在正平衡点和边界平衡点，所以系统不存在位于第一象限内部的极限环(因为极限环内部必须要有平衡点)，同时由定理3.1可知， $E_0\left(0,0\right)$ 是稳定的结点。所以 $E_0\left(0,0\right)$ 是全局渐近稳定的。

定理3.2当 $0<A<A^{\text{*}}$ 时，系统(4)的边界平衡点 $E_1\left(x_1,0\right)$ 有以下结论：

1) 如果 $0<x_1<1$，则 $E_1\left(x_1,0\right)$ 是鞍点；

2) 如果 $x_1>1$，则 $E_1\left(x_1,0\right)$ 是不稳定的。

证明：矩阵 $J\left(x,0\right)$ 在点 $E_1$ 处的行列式和迹分别为

$\begin{array}{l}\text{Det}\left[J\left(E_1\right)\right]=-s{x}_1\sqrt{\Delta }\left(1-x_1\right)\left(x_1+A\right),\\ \text{Tr}\left[J\left(E_1\right)\right]=x_1\sqrt{\Delta }-s\left(1-x_1\right)\left(x_1+A\right).\end{array}$

所以当 $0<x_1<1$ 时，有 $\text{Det}\left[J\left(E_1\right)\right]<0$，即 $E_1\left(x_1,0\right)$ 是鞍点。当 $x_1>1$ 时，有 $\text{Det}\left[J\left(E_1\right)\right]>0$ 和 $\text{Tr}\left[J\left(E_1\right)\right]>0$，那么 $E_1\left(x_1,0\right)$ 是不稳定的。

定理3.2证明完毕。

定理3.3当 $0<A<A^{\text{*}}$ 时，系统(4)的边界平衡点 $E_2\left(x_2,0\right)$ 有以下结论：

1) 如果 $0<x_2<1$，则 $E_2\left(x_2,0\right)$ 是稳定的；

2) 如果 $x_2>1$，则 $E_2\left(x_2,0\right)$ 是鞍点。

证明：矩阵 $J\left(x,0\right)$ 在点 $E_2$ 在处的行列式和迹分别为

$\begin{array}{l}\text{Det}\left[J\left(E_2\right)\right]=s{x}_2\sqrt{\Delta }\left(1-x_2\right)\left(x_2+A\right),\\ \text{Tr}\left[J\left(E_2\right)\right]=-x_2\sqrt{\Delta }-s\left(1-x_2\right)\left(x_2+A\right).\end{array}$

所以当 $0<x_2<1$ 时，有 $\text{Det}\left[J\left(E_2\right)\right]>0$ 和 $\text{Tr}\left[J\left(E_2\right)\right]<0$，那么 $E_2\left(x_2,0\right)$ 是稳定的。当 $x_2>1$ 时，有 $\text{Det}\left[J\left(E_2\right)\right]<0$，则 $E_2\left(x_2,0\right)$ 是鞍点。

定理3.3证明完毕。

定理3.4当 $A=A^{\text{*}}$ 时，系统(4)的边界平衡点 $E^{*}\left(x^{*},0\right)$ 有以下结论：

1) 如果 $d<a<{\left(\sqrt{d}+\frac{1}{\sqrt{d}}\right)}^2$，那么 $E^{*}\left(x^{*},0\right)$ 是吸引的鞍结点；

2) 如果 $a>{\left(\sqrt{d}+\frac{1}{\sqrt{d}}\right)}^2$，那么 $E^{*}\left(x^{*},0\right)$ 是排斥的鞍结点。

证明：当 $A=A^{\text{*}}$ 时，系统(4)在 $E^{*}$ 处的雅克比矩阵为

$J\left(E^{*}\right)=\left(\begin{array}{cc}0& -x^{*}\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right)\left(1+k\sqrt{ad}\right)\\ 0& -s\sqrt{a}\left(1-x^{\text{*}}\right)\left(\sqrt{a}-\sqrt{d}\right)\end{array}\right),$

并且矩阵 $J\left(E^{\text{*}}\right)$ 的行列式和迹分别为

$\text{Det}\left[J\left(E^{\text{*}}\right)\right]=0,\text{Tr}\left[J\left(E^{\text{*}}\right)\right]=-s\sqrt{a}\left(1-x^{\text{*}}\right)\left(\sqrt{a}-\sqrt{d}\right).$

当 $x^{*}\ne 1$，即 $a\ne {\left(\sqrt{d}+\frac{1}{\sqrt{d}}\right)}^2$ 时，则矩阵 $J\left(E^{\text{*}}\right)$ 有一个零特征值。作变换 $u=x-x^{\text{*}}$ 和 $v=y$，将边界平衡点 $E^{*}$ 平移到原点，并在原点进行泰勒展开，可得：

$\begin{array}{l}\stackrel{\dot{}}{u}=a_{10}u+a_{01}v+a_{20}{u}^2+a_{11}uv+a_{02}{v}^2+o\left({\left|u,v\right|}^2\right),\\ \stackrel{\dot{}}{v}=b_{10}u+b_{01}v+b_{20}{u}^2+b_{11}uv+b_{02}{v}^2+o\left({\left|u,v\right|}^2\right),\end{array}$ (8)

其中

$\begin{array}{l}{a}_{10}=0,a_{01}=-x^{*}\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right)\left(1+k\sqrt{ad}\right),a_{20}=-x^{*},a_{11}=-2ak{x}^{*}-a+d,\\ a_{02}=-x^{*}k\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right),b_{10}=0,b_{01}=-s\sqrt{a}\left(1-x^{*}\right)\left(\sqrt{a}-\sqrt{d}\right),b_{20}=0,\\ b_{11}=s\left(a-d-1\right),b_{02}=-sk\sqrt{a}\left(1-x^{*}\right)\left(\sqrt{a}-\sqrt{d}\right).\end{array}$

为了将系统(8)化为标准型，作变换

$\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{cc}1& -x^{*}\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right)\left(1+k\sqrt{ad}\right)\\ 0& -s\sqrt{a}\left(1-x^{\text{*}}\right)\left(\sqrt{a}-\sqrt{d}\right)\end{array}\right)\left(\begin{array}{c}X\\ Y\end{array}\right),$

且作时间变换 $\text{d}\tau =-s\sqrt{a}\left(1-x^{\text{*}}\right)\left(\sqrt{a}-\sqrt{d}\right)\text{d}t$ (仍使用t代替 $\tau$ )，那么系统(8)可以写成

$\begin{array}{l}\stackrel{\dot{}}{X}=c_{20}{X}^2+c_{11}XY+c_{02}{Y}^2+o\left({\left|X,Y\right|}^2\right),\\ \stackrel{\dot{}}{Y}=Y+d_{20}{X}^2+d_{11}XY+d_{02}{Y}^2+o\left({\left|X,Y\right|}^2\right),\end{array}$ (9)

其中

$\begin{array}{l}{c}_{20}=\frac{x^{*}}{s\left(\sqrt{a}-\sqrt{d}\right)\left(1-x^{*}\right)},c_{11}=-\frac{P}{s\left(1-x^{*}\right)},c_{02}=\frac{\left(\sqrt{a}-\sqrt{d}\right)Q}{s\left(1-x^{*}\right)},d_{20}=0,\\ d_{11}=-\frac{a-d-1}{\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right)\left(1-x^{*}\right)},d_{02}=\frac{x^{*}\left(1+k\sqrt{ad}\right)}{1-x^{*}},\\ P=2x^{*}\left(1+k\sqrt{ad}\right)+s\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right)-ks{x}^{*}\sqrt{a}\left[a\sqrt{d}-\left(1+d\right)\left(2\sqrt{a}-\sqrt{d}\right)\right]ks,\end{array}$

$\begin{array}{c}Q=-a^{\frac{3}{2}}{\left[x^{*}\left(1-x^{*}\right)ks\right]}^2-a^{\frac{3}{2}}\sqrt{d}{x}^{*2}\left(a\sqrt{d}-2\sqrt{a}d+d^{\frac{3}{2}}-2\sqrt{a}+\sqrt{d}\right)k^{2}s\\ -ad\left(a^2\sqrt{d}-4a^{\frac{3}{2}}d+6a{d}^{\frac{3}{2}}-4a{d}^2+d^{\frac{5}{2}}-3a^{\frac{3}{2}}+7a\sqrt{d}+2d^{\frac{3}{2}}\right)ks\\ +\sqrt{a}{x}^{*3}{\left(1+k\sqrt{ad}\right)}^2+s\sqrt{a}{x}^{*}\left(\sqrt{a}-\sqrt{d}\right).\end{array}$

由文 [9] 中定理7.1， $E^{*}$ 是鞍结点。注意到 $X^2$ 的系数为 $c_{20}$，当 $d<a<{\left(\sqrt{d}+\frac{1}{\sqrt{d}}\right)}^2$ 时， $c_{20}>0$，时间变换为负，那么 $E^{*}$ 是吸引的鞍结点；当 $a>{\left(\sqrt{d}+\frac{1}{\sqrt{d}}\right)}^2$ 时， $c_{20}<0$，时间变换为正，那么 $E^{*}$ 是排斥的鞍结点。

定理3.4证明完毕。

下面讨论系统(4)的正平衡点的稳定性。在正平衡点 $E_3\left(1,y_1\right)$ 处的雅克比矩阵为：

$J\left(E_3\right)=\left(\begin{array}{cc}a-\left(1+k{y}_1\right)\left(A+2+d+y_1\right)& -\left(1+A\right)\left(dk+2k{y}_1+k+1\right)\\ s{y}_1\left(1+A\right)\left(1+k{y}_1\right)& 0\end{array}\right),$

并且矩阵 $J\left(E_3\right)$ 的行列式和迹分别为

$\begin{array}{l}\text{Det}\left[J\left(E_3\right)\right]=s{y}_1\left(1+k{y}_1\right){\left(1+A\right)}^2\left(dk+2k{y}_1+k+1\right)>0,\\ \text{Tr}\left[J\left(E_3\right)\right]=a-\left(1+k{y}_1\right)\left(A+2+d+y_1\right).\end{array}$

定义 $k^{*}=\frac{1}{y_1}\left(\frac{a}{A+2+d+y_1}-1\right)$。

定理3.5当 $0<A<\frac{a}{1+d}-1$ 时，有以下结论：

1) 如果 $0<k<k^{*}$，那么系统(4)的唯一正平衡点 $E_3$ 是不稳定的；

2) 如果 $k>k^{*}$，那么系统(4)的唯一正平衡点 $E_3$ 是稳定的；

3) 如果 $k=k^{*}$，那么系统(4)的唯一正平衡点 $E_3$ 是中心或细焦点。

证明：如果 $0<k<k^{*}$，那么 $\text{Tr}\left[J\left(E_3\right)\right]>0$，则系统(4)的正平衡点 $E_3$ 是不稳定的。如果 $k>k^{*}$，那么 $\text{Tr}\left[J\left(E_3\right)\right]<0$，则系统(4)的正平衡点 $E_3$ 是稳定的。如果 $k=k^{*}$，那么 $\text{Tr}\left[J\left(E_3\right)\right]=0$，则系统(4)的正平衡点 $E_3$ 是中心或细焦点。

定理3.5证明完毕。

4. 分支分析

根据定理2.1，除边界平衡点 $E_0$ 外，当 $0<A<A^{\text{*}}$ 时，系统(4)存在边界平衡点 $E_1\left(x_1,0\right)$ 和 $E_2\left(x_2,0\right)$ ；当 $A=A^{\text{*}}$ 时，系统(4)存在边界平衡点 $E^{*}\left(x^{*},0\right)$ ；当 $A^{*}<A<a-d$ 时，系统(4)不存在边界平衡点。由上述分析，选取参数A作为分支参数，当参数A在阈值 $A^{\text{*}}$ 附近改变时，边界平衡点的个数发生改变，所以系统会发生鞍结分支。

定理4.1设 $x^{*}\ne 1$，当系统(4)的参数A满足条件 $A=A_{SN}=A^{\text{*}}$ 时，系统(4)会在 $E^{*}\left(x^{*},0\right)$ 处发生鞍结分支。

证明：系统(4)在点 $E^{*}\left(x^{*},0\right)$ 处的雅克比矩阵为

$J\left(E^{*};A_{SN}\right)=\left(\begin{array}{cc}0& -x^{*}\sqrt{a}\left(\sqrt{a}-\sqrt{d}\right)\left(1+k\sqrt{ad}\right)\\ 0& -s\sqrt{a}\left(1-x^{\text{*}}\right)\left(\sqrt{a}-\sqrt{d}\right)\end{array}\right).$

通过计算，当 $x^{*}\ne 1$ 时，矩阵 $J\left(E^{*};A_{SN}\right)$ 有一个零特征值。令V和W是矩阵 $J\left(E^{*};A_{SN}\right)$ 和 $J^{\text{T}}\left(E^{*};A_{SN}\right)$ 零特征值的特征向量，通过计算得到

$V=\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right),W=\left(\begin{array}{c}{W}_1\\ W_2\end{array}\right)=\left(\begin{array}{c}1\\ -\frac{x^{*}\left(1+k\sqrt{ad}\right)}{s\left(1-x^{*}\right)}\end{array}\right).$

之后令

$F\left(x,y\right)=\left(\begin{array}{c}{F}_1\\ F_2\end{array}\right)=\left(\begin{array}{c}x\left[ax-\left(d+x+y\right)\left(1+ky\right)\left(A+x\right)\right]\\ sy\left(x-1\right)\left(1+ky\right)\left(A+x\right)\end{array}\right).$

那么

$\begin{array}{l}{F}_A\left(E^{*};A_{SN}\right)=\left(\begin{array}{c}-x^{*}\left(d+x^{*}\right)\\ 0\end{array}\right),\\ D^{2}F\left(E^{*};A_{SN}\right)\left(V,V\right)={\left(\begin{array}{c}\frac{{\partial }^2{F}_1}{\partial x^2}{V}_1^2+2\frac{{\partial }^2{F}_1}{\partial x\partial y}{V}_1{V}_2+\frac{{\partial }^2{F}_1}{\partial y^2}{V}_2^2\\ \frac{{\partial }^2{F}_2}{\partial x^2}{V}_1^2+2\frac{{\partial }^2{F}_2}{\partial x\partial y}{V}_1{V}_2+\frac{{\partial }^2{F}_2}{\partial y^2}{V}_2^2\end{array}\right)}_{\left(E^{*};A_{SN}\right)}=\left(\begin{array}{c}-2x^{*}\\ 0\end{array}\right).\end{array}$

通过计算可知

$W^{\text{T}}\cdot F_A\left(E^{*};A_{SN}\right)=-x^{*}\left(d+x^{*}\right)\ne 0,$

$W^{\text{T}}\cdot D^{2}F\left(E^{*};A_{SN}\right)\left(V,V\right)=-2x^{*}\ne 0.$

由 [10] 中的Sotomayor’s定理，可知系统(4)在 $E^{\text{*}}$ 处发生鞍结分支。

定理4.1证明完毕。

5. 数值模拟

根据定理3.4，当 $A=A^{\text{*}}$ 时，系统(4)的边界平衡点 $E^{*}\left(x^{*},0\right)$ 是鞍结点。

例1对于系统(4)，选取参数 $a=2.25$， $d=1$， $A=A^{*}=0.25$， $k=0.5$， $s=0.5$，边界平衡点 $E^{*}\left(0.5,0\right)$ 是吸引的鞍结点(见图1)。

由图1可知，系统表现出双稳现象，一部分轨线趋向于原点，另一部分轨线趋向于 $E^{*}$，也就是初值条件在不同的区域内，食饵和捕食者有可能同时绝灭，或者稳定于边界平衡点 $E^{*}$，即食饵不绝灭，捕食者绝灭。

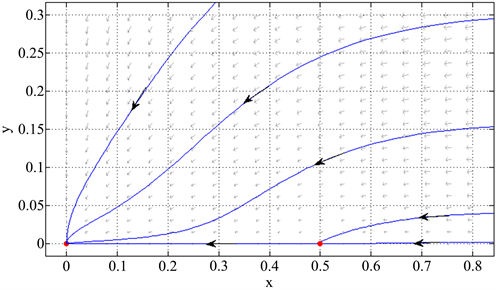
Figure 1. When $a=2.25$, $d=1$, $A=0.25$, $k=0.5$, $s=0.5$, $E^{*}$ is an attracting saddle-node

图1. 当 $a=2.25$， $d=1$， $A=0.25$， $k=0.5$， $s=0.5$， $E^{*}$ 是吸引的鞍结点

根据定理3.5，当 $0<k<k^{*}$ 时， $E_3$ 是不稳定的；当 $k>k^{*}$ 时， $E_3$ 是稳定的；当 $k=k^{*}$ 时， $E_3$ 是中心或细焦点。当k的数值在 $k=k^{*}$ 处发生改变时， $E_3$ 的稳定性也会发生改变，因此在 $E_3$ 处可能存在Hopf分支。下面通过数值模拟来验证Hopf分支的结果。

例2对于系统(4)，选取参数 $a=5$， $d=0.5$， $A=1$， $k=k^{*}=0.5$， $s=1$，此时 $\text{Tr}\left[J\left(E_3\right)\right]=0$，通过计算可知一阶焦点量 $l_1\approx -44.933<0$。扰动参数k，使 $k=k^{*}$ 减小到 $k=k_1=0.5-0.01$，那么系统(4)产生超临界Hopf分支，并且在 $E_3\left(1,0.5\right)$ 附近出现了一个稳定的极限环(见图2)。

由图2可知，系统的吸引域分成两部分，一部分轨线趋向于原点，也就是食饵和捕食者都绝灭，另一部分轨线趋向于稳定的极限环，也就是食饵和捕食者的种群是周期振荡，食饵和捕食者能够共存。

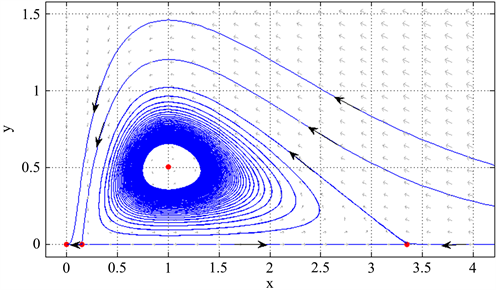
Figure 2. When $a=5$, $d=0.5$, $A=1$, $k=0.5-0.01$, $s=1$, there exists a stable limit cycle around $E_3$

图2. 当 $a=5$， $d=0.5$， $A=1$， $k=0.5-0.01$， $s=1$， $E_3$ 附近出现了一个稳定的极限环

下面讨论恐惧效应对系统的动力学性质的影响。当没有恐惧效应时(即 $k=0$，见图3)，这时正平衡点是不稳定的，食饵和捕食者都绝灭。保持其它参数不变，考虑恐惧效应的影响(即 $k=0.5$，见图2)，这时正平衡点仍然是不稳定的，但是出现了稳定的极限环的，系统出现双稳现象，即食饵和捕食者有可能都绝灭或者趋向于周期振荡。增大恐惧效应(即 $k=1$，见图4)，这时正平衡点变成稳定的，系统也出现双稳现象，即食饵和捕食者有可能都绝灭或者两者同时趋向于一个稳定的值。所以增大恐惧效应，会使得正平衡点从不稳定变成稳定，也就是较大的恐惧效应可以促进系统的稳定。

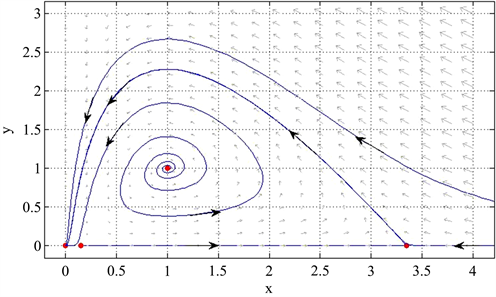
Figure 3. When $a=5$, $d=0.5$, $A=1$, $k=0$, $s=1$, $E_3$ is unstable

图3. 系统(4)中，当 $a=5$， $d=0.5$， $A=1$， $k=0$， $s=1$， $E_3$ 是不稳定的

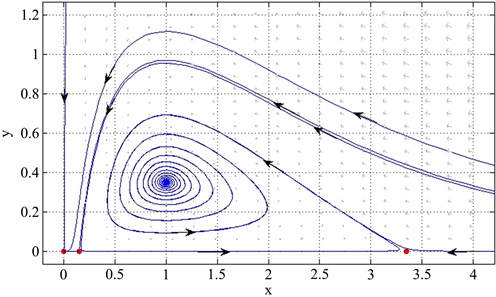
Figure 4. When $a=5$, $d=0.5$, $A=1$, $k=1$, $s=1$, $E_3$ is stable

图4. 系统(4)中，当 $a=5$， $d=0.5$， $A=1$， $k=1$， $s=1$， $E_3$ 是稳定的

6. 结论

本文中，我们讨论了具有Allee效应和恐惧效应的捕食–食饵模型动力学行为。讨论系统(1)的平衡点存在性和稳定性。当系统的原点 $E_0$ 是局部渐进稳定的，若食饵出生率充分小和Allee效应参数A充分大时( $d<a\le d+1$ 和 $A>A^{*}$ )，系统只存在边界平衡点 $E_0$，此时 $E_0$ 是全局渐进稳定，这意味着食饵和捕食者都将趋于灭绝。故当Allee效应越强时，越不利于食饵和捕食者种群生存。同时当k的数值在 $k=k^{*}$ 处发生改变时， $E_3$ 的稳定性也会发生改变，通过数值模拟，我们验证了系统(4)存在Hopf分支，导致系统会出现双稳现象，也就是轨线趋向于原点或者稳定的极限环，同时较大的恐惧效应可以使极限环消失，并且正平衡点是稳定的，所以较大的恐惧效应会促进系统的稳定。