基于PCA的土壤含水量高光谱反演模型比较研究

Comparison of Hyperspectral Soil Water Content Inversion Models Based on PCA

摘要: 土壤含水量(SMC)是农作物生长过程中的重要指标之一，快速测定土壤水分状况对于农业发展极为重要。针对高光谱波段信息冗余和共线性特点以及光谱测定中无关信息和噪声带来的影响，对原始光谱进行倒数对数一阶微分变换预处理，利用主成分分析(PCA)对光谱信息进行降维，提取出12个主成分作为自变量；利用偏最小二乘、支持向量机、随机森林、BP神经网络建立SMC预测模型并进行综合对比分析。结果表明：利用PCA对光谱信息降维后的主成分建立的模型均有良好的预测能力，选取的主成分累积贡献率达到92%以上；通过对光谱变换前后模型的综合对比可以发现PCA-RF模型精度最高(R2分别为0.8362，0.9630，RPD分别为2.4229、3.7019)。

Abstract: Soil moisture content (SMC) is one of the important indexes in the process of crop growth. How to quickly measure soil moisture is very important. In the previous SMC water content inversion research, the characteristic band and linear empirical model are mostly used to construct the inversion model, and the characteristics of hyperspectral band information redundancy and collinearity are not fully considered, so the prediction ability of the model needs to be improved. In order to reduce the influence of irrelevant information and noise in spectral determination, the original spectrum was preprocessed by reciprocal logarithm first-order differential transformation; In order to weaken the redundancy and collinearity of hyperspectral band information, principal component analysis (PCA) is used to reduce the dimension of the original spectral information, and 12 principal components are extracted as independent variables; The SMC prediction model is established by using partial least squares, support vector machine, random forest and BP neural network. The results show that PCA has good prediction ability for the principal component model after spectral dimensionality reduction, and the cumulative contribution rate of the selected principal component is 99.99%; Through the comprehensive comparison of the models before and after spectral transformation, it can be found that the accuracy of PCA-RF model is the highest (R2 is 0.8362 and 0.9630 respectively, RPD is 2.4229 and 3.7019 respectively).

1. 引言

土壤含水量(soil moisture content, SMC)是影响农作物生长、发育和墒情监测的重要因素之一，也是农业灌溉、管理决策中重要的基础数据 [1]。通过快速、准确的SMC监测可以判定出农作物所需求的水分指标，对农业生产建设具有建设性的指导意义，传统的SMC监测方法费时费力、成本高昂，迫切需要采用一个高效准确可信度高的监测方式 [2]。高光谱遥感具有光谱分辨率高、波段连续性强、信息量丰富、无损零污染等特点 [3] [4]。

利用高光谱技术来快速监测土壤含水量已成为近年来的一个研究热点 [5]。Tao Song等 [6] 利用高光谱数据分析与SMC的敏感波段，建立单线性回归模型预测土壤水含量；Gao Y等 [7] 利用了多元线性回归(SMLR)和偏最小二乘法(PLSR)等线性回归方法建立了土壤含水量反演模型，并发现在一阶土壤反射率的基础上模型精度较高；Xia K等 [8] 通过相关系数方法挑选出敏感特征波段，将特征波段组合成光谱指数建立了偏最小二乘法(PLSR)对研究区土壤含水量进行反演。目前国内外在选择建立土壤含水量反演模型的方式上大多利用特征波段或光谱指数建立线性回归模型，虽然取得了较好的效果，但其实高光谱数据具有波段信息冗余、共线性、噪声的问题，针对这一问题，大多数学者只是通过相关性分析的方法挑选出几个敏感特征波段，丢失了大量重要的信息，且仅用几个波段与土壤某一个属性之间的关系不具有得到最优预测解的可能性 [9]。因此选择一种可以充分代表波段信息又减少了输入变量的方法极为重要。当前研究中建立土壤含水量模型多采用多元线性回归或偏最小二乘回归法等线性回归模型，较少使用非线性模型来预测土壤含水量 [10]。因此简单地使用线性模型不能够充分说明它们之间的关系。

本文以贵阳市花溪区采集的农田土壤样品为研究对象，针对高光谱土壤水分反演中波段信息噪声、共线性、冗余等问题，利用PCA算法对光谱信息降维，以获取的主成分为自变量建立多种土壤含水量反演模型，对比筛选出最有效的土壤含水量反演模型，验证了基于PCA算法实现土壤含水量高精度反演的可行性，以期为实现高光谱影像快速、精确土壤水分含量区域反演及监测提供科学技术基础和参考。

2. 试验材料与方法

2.1. 研究区概况与土样采集

以贵州省贵阳市花溪区(106˚27'~106˚352'E, 26˚11'~26˚34'N)为研究区，花溪区地貌主要为山地、丘陵，处云贵高原东斜坡和苗岭山脉中段，为典型的喀斯特地质区域，总面积大约964 km²，平均海拔高度为1100 m左右，属于亚热带温润温和型气候，年平均气温在15.5℃，年平均降水1215.70 mm。根据研究区耕地的分布状况和地理条件合理布设50个采样点，使用直径、深度分别为7.2 cm、5 cm的环刀采集黄壤土壤样品，采集时剔除表层杂草、碎石等，保持土壤原状，同时使用GPS记录采样点坐标，将环刀密封编号后称重记录。

2.2. 土壤光谱与含水量测定

研究选用ASD FieldSpec4地物光谱仪在暗室中测定土样反射率光谱，该仪器波段范围为350~2500 nm，采样间隔分为1.4 nm (波段350~1000 nm)、2 nm (波段1000~2500 nm)，经重采样后变为1 nm间隔。在暗室中将土样置于实验黑色器皿中并刮平土壤表面，光谱测定使用高探头测量，测定光谱时需要贴紧土壤表面，测量前需要校准标准白板的参数并去除暗电流，在土壤表面4个不同位置测量，在每个位置上采集5条光谱曲线，共采集20条光谱曲线，利用ViewSpecPro求其平均值作为土样的反射率光谱数据，由于350~399、2451~2500 nm范围光谱在测定时噪声比较大，故剔除这两个范围波段后作为原始数据。待光谱测量完毕之后，将土样放入铝盒中称重，记为 $w_a$，并记录铝盒编号。将土样放入烘干机中进行烘干实验，时间为24 h，温度为110℃，待土样烘干之后，分别测定土样加铝盒及单独铝盒的重量，记为 $w_b$ 、 $w_c$，SMC的计算公式为：

$\text{SMC}=\frac{w_a-w_c}{w_b-w_c}\times 100\%$ (1)

2.3. 光谱数据预处理与主成分分析

通过光谱对数微分变换可以去除或减少土样表面粗糙度不一致、观测光照强度变化对目标光谱产生的影响，能够增强光谱特征、去除背景噪声 [11]，故对原始数据进行倒数对数的一阶导数变换。计算公式如下：

$\log \text{'}\left(1/R\left({\lambda }_i\right)\right)=\left[\log \left(1/R\left({\lambda }_{i+1}\right)\right)-\log \left(1/R\left({\lambda }_{i-1}\right)\right)\right]/\left({\lambda }_{i+1}-{\lambda }_{i-1}\right)$ (2)

式中 ${\lambda }_i$ 、 ${\lambda }_{i-1}$ 、 ${\lambda }_{i+1}$ 表示各相邻波长。

主成分分析(Principal components analysis, PCA)是一种可靠性强、使用最广泛的数据降维算法 [12]，PCA的思想是将m维特征向量映射到n维特征向量上，即将高维特征转换为少数几个主成分，且主成分之间互不相关，并使其具有最大信息量，从而达到简化数据的目的。假定包含有m个样本、n个特征指标的数据集，则其可以构成矩阵：

$X=\left(\begin{array}{ccc}{x}_{11}& \dots & x_{1n}\\ ⋮& \ddots & ⋮\\ x_{m1}& \cdots & x_{mn}\end{array}\right)=\left(x_1,x_2,\cdots ,x_n\right)$ (3)

PCA主要步骤如下：

1) 首先将矩阵X进行标准化变换，其均值为 ${\bar{x}}_n=\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{x}_{in}}$，标准差为 $S_n=\sqrt{\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{\left(x_{in}-{\bar{x}}_n\right)}^2/\left(n-1\right)}\right)}$，标准化公式为：

$X_{mn}=\frac{x_{mn}-{\bar{x}}_n}{S_n}$ (4)

原始矩阵经过标准化得到矩阵 $X=\left(X_1,X_2,\cdots ,X_n\right)$。

2) 计算矩阵X的协方差矩阵及其对应的特征值和特征向量，若满足

$\{\begin{array}{l}{B}_1=a_{11}{X}_1+a_{12}{X}_2+\cdots +a_{1n}{X}_n\\ B_2=a_{21}{X}_1+a_{22}{X}_2+\cdots +a_{2n}{X}_n\\ ⋮\\ B_m=a_{m1}{X}_1+a_{m2}{X}_2+\cdots +a_{mn}{X}_n\end{array}$ (5)

且 $a_{11}^2+a_{12}^2+\cdots +a_{1n}^2=1$ 、 $\text{Var}\left(B_1\right)$ 值最大，则称 $B_1$ 为原数据的第一主成分；若 $a_{21}^2+a_{22}^2+\cdots +a_{2n}^2=1$， $\left(a_{21},a_{22},\cdots ,a_{2n}\right)$ 与 $\left(a_{11},a_{12},\cdots ,a_{1n}\right)$ 向量垂直，且 $\text{Var}\left(B_2\right)$ 值最大，则称 $B_2$ 为原数据的第二主成分；可以由此推出第三、第四，……，等n个主成分。通常选取累计方差贡献率达到90%以上的前h个主成分，可以有效减少主成分的个数，同时保证了信息量的可靠性，并将选取的h个主成分作为模型的输入变量。

2.4. 土壤含水量反演模型的建立与验证

研究采用线性模型PLSR和非线性模型RF、BPN、SVM综合分析对比SMC预测能力。通过对反射率光谱以及光谱变换后进行主成分分析筛选出主成分，选其作为自变量、SMC为因变量建立模型估算土壤含水量。PLSR是一种在高光谱遥感模型中广泛使用的新型统计方法，它可以很好的解决高光谱反演中自变量数据之间存在的多重共线性的问题 [13]。BPN神经网络是一种多层的前馈神经网络，主要包含输入层、隐含层和输出层，可以满足复杂的多维函数映射需求，仅需通过训练数据进行自身的训练，得到某种映射关系，就可以给出最接近期望值的结果 [14]。RF是以决策树为基学习器构建Bagging集成的基础上，进一步构建无数个小决策数引入随机属性选择，使得最终集成的泛化性能可通过个体学习器之间的差异度的增加而进一步提升 [15]。SVM是一种基于统计学的模式识别方法，它在解决小样本、非线性、高维数据集的回归问题上有许多独特的优点 [16]。

模型的精度评价指标选用决定系数(R²)、均方根误差(RMSE)、相对分析误差(RPD)，通常越好的模型，其R²和RPD越高，而RMSE越低 [17]。R²的值越接近1越代表模型的估测效果好，RPD的值大于2时代表模型具有非常好的估测能力，RPD的值在区间[1.4, 2]时代表模型具有较好的估测能力，RPD的值小于1.4时代表模型不具备估测能力。

3. 结果与分析

3.1. 土壤含水量概况

从表1可以看出，样本划分为37个训练集和13个验证集，训练集、验证集SMC的平均值分别为0.156、0.154，总样本的SMC均值为0.155，且变异系数为0.407，介于训练集0.385和验证集0.455之间，属于中等变异。

Table 1. Description and statistics of SMC

表1. 土壤含水量描述统计

3.2. 光谱变换与PCA主成分分析

土壤样本的原始反射率光谱曲线如图1(a)所示，所有的光谱曲线走势大致一致且总体呈下降趋势，在可见光波段范围内反射率快速变化，在近红外波段后整体变化速率较为缓慢，可以发现土壤水分在1400、1900、2200 nm波段附近存在明显的吸收峰。图1(b)为经过倒数对数的一阶导数变换后的光谱曲线，所有的光谱曲线走势相同且在小范围波段发生剧烈变化，在1400、1900 nm波段附近形成较明显的波峰。

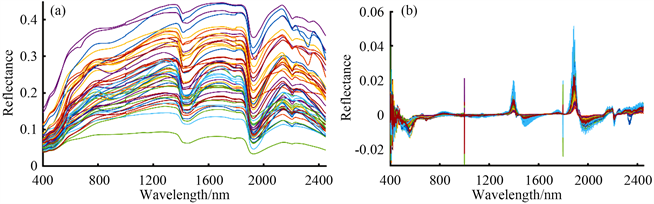
Figure 1. (a) The original reflectance spectrum curve; (b) The first derivative reflectance spectral curve of reciprocal logarithm

图1. (a) 原始反射率光谱曲线；(b) 倒数对数的一阶导数反射率光谱曲线

研究利用PCA算法对光谱2050个波段降维并筛选主成分。通过对土样反射率数据以及对数微分预处理后的数据进行主成分分析后，按照通常研究中选取主成分累积贡献率达到90%以上的要求，选出前12个主成分分量，如表2所示。选取了PCA降维后前12个主成分，光谱原始反射率以及倒数对数一阶导数反射率曲线的各主成分累积贡献率分别为99.996%、92.061%。将PCA降维后获取的12个主成分作为自变量输入模型。

Table 2. The principal component contribution rate of soil spectrum

表2. 土壤光谱主成分贡献率

3.3. SMC反演模型建立与检验

3.3.1. 原始光谱建模

利用PCA对原始光谱数据提取主成分光谱特征，将12个主成分作自变量，SMC作为因变量，得到PCA-PLSR、PCA-SVM、PCA-BPN、PCA-RF四种SMC反演模型，模型精度评价如图2(a)所示。由图2(a)、表3可得：PCA-RF的决定系数(R² = 0.8362)最高，RPD值达到2.4229，表明了PCA-RF模型的预测能力非常好，是优异的SMC预测模型；PCA-BPN的预测能力次之，同样具有良好的预测能力，R²和RPD分别为0.7844、2.1835；而PCA-SVM和PLSR的预测能力稍差一些，R²分别为0.7646、0.7234，RPD值都大于1.8，具有较好的预测能力。客观的说，通过PCA主成分建立的SMC估测模型具有良好的预测效果。

3.3.2. 倒数对数的一阶导数光谱建模

基于PCA对倒数对数的一阶微分光谱进行4种反演模型构建[图2(b)]，其模型精度评价如表3所示。根据图2(b)以及表3可知，PCA-RF模型的反演能力仍是最好的，其R²高达0.9630，RPD值为3.7019，表明其具有非常好的预测精度；PCA-BPN次之，其R²为0.8642，RPD为2.7942，模型的精度也很好；PCA-SVM的R²为0.8571，RPD为2.7624；而PCA-PLSR反演精度最低，其R²为0.7341，RPD为1.9095。

3.3.3. 模型对比分析

根据图3中不同模型的拟合效果可知，4种模型的中PCA-RF模型在光谱对数微分变换前后的精度都是最高的，PLSR精度最低，在进行对数微分变换后各模型预测能力都得到了提升，其中PCA-RF提升效果最为明显，其R²值提高了15.16%；RPD值提高了52.79%；其次为PCA-SVM模型，其R²值提高了12.1%；RPD值提高了42.8%；PCA-BPN模型，其R²值提高了10.17%；RPD值提高了27.97%；而PCA-PLSR模型提升不明显。

通过各模型的预测精度对比可以发现，非线性模型PCA-BPN、PCA-RF、PCA-SVM的预测能力优于线性模型PCA-PLSR，光谱对数微分变换可以有效的提升模型的预测能力，其能够降低光谱测定中背景噪声、无关信息带来的影响。

4. 讨论

光谱数学变换可以极大的消除光谱测定中不同背景、噪声带来的影响 [17]。本文选用对数微分变换算法对原始光谱进行预处理，利用PCA算法对变换前后的数据降维提取主成分，结合RF、BPN、SVM、PLSR建立不同的土壤含水量估测模型，比较选出最佳SMC预测模型。一般研究中，通常选择累积方差贡献率达到90%以上的主成分个数，本文中选取的12个主成分累积方差贡献率达到了92%以上，非常具有代表原始信息的能力，同时也简化了模型输入自变量，提高了模型运算速度。

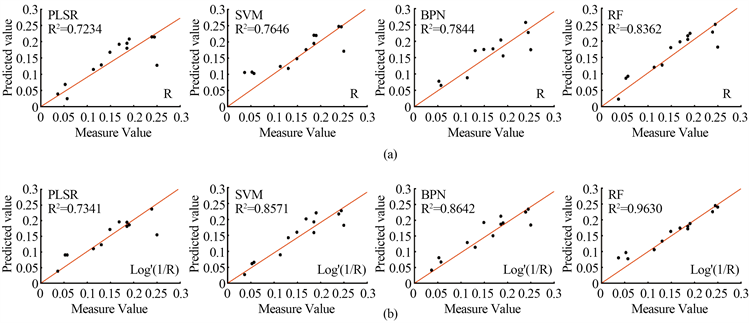
Figure 2. (a) Scatter diagram of different prediction models of original spectrum; (b) Scatter diagram of different prediction models of first-order differential spectrum of reciprocal logarithm

图2. (a) 原始光谱不同预测模型散点图；(b) 倒数对数的一阶微分光谱不同预测模型散点图

Figure 3. The original spectrum reciprocal logarithm first-order differential comparative analysis diagram

图3. 原始光谱–倒数对数一阶微分对比分析图

Table 3. Accuracy analysis of different models based on original spectrum reciprocal log differential spectrum

表3. 基于原始光谱–倒数对数微分光谱不同模型精度分析

通过对比不同SMC估测模型可以发现，在对光谱数据预处理后，除了线性模型提升不明显以外，非线性模型的精度都得到了较大提升，其R²值都高于0.8，表明了光谱对数微分变换处理能提高模型预测的精度。这主要是因为对数微分变换可以去除光谱测定中不同背景、噪声的影响，特别是一阶微分可以最大的消除一次方项噪声的影响，提高光谱分辨率和灵敏度 [18]。目前在土壤水含量以及有机质反演研究中，已经证明了对数微分变换处理能有效提高模型的预测精度 [19]。在本研究中也证明了光谱对数微分预处理对于模型的预测能力有很好提升效果，且非线性模型的预测能力要优于线性模型。通常情况下土壤光谱会受到土壤质地、有机质含量、土壤颗粒大小等的影响，其反射光谱会随之产生变化 [20]。本次研究的土壤为单一黄壤土壤，未考虑其他土壤质地和不同有机质含量对模型的影响，所以还需要考虑在其他背景条件下模型的预测效果；研究主要选用PCA算法对高光谱数据进行降维，虽然取得了很好的效果，但并未考虑其他降维算法，有待进一步研究。

5. 结论

本文以贵阳市花溪区50个不同含水量土壤样本为研究对象，以其室内光谱和土壤含水量为基础，利用光谱变换结合PCA算法提取出的主成分为自变量，建立了不同的SMC估测模型，并对其进行综合对比分析得出：1) 经过倒数对数一阶微分变换后建立的模型预测能力得到了有效提升，非线性模型的提升效果明显优于线性模型，表明倒数对数一阶微分变换可以有效降低光谱测定中无关信息和噪声带来的影响。2) 利用PCA提取出的12个主成分建立的模型均具有很好的预测能力，表明通过PCA可以有效地简化数据量。3) 光谱变换后PCA-RF模型预测能力最优，R²和RPD分别为0.9630、3.7019，表明PCA-RF模型在SMC估测中更为有效。

基金项目

贵州省科技支撑计划项目(黔科合支撑[2021]一般496)。

NOTES

^*通讯作者。