基于共享停车的停车请求决策与车位分配模型

Decision-Making and Parking Slots Allocation Model of Parking Requests Considering Sharing Parking

摘要: 为提高城市停车位的时空资源利用率，本文基于单个停车场共享停车位的实时状态，动态收集停车请求数据，以停车场时空资源可持续利用性最大化为目标，同时考虑停车场的收益，建立了两阶段动态化车位分配模型并采用隐枚举法进行求解，从而对停车请求做出决策并为通过的停车请求分配车位。算例分析表明，相比传统先到先得的车位分配方式，本文提出的两阶段动态化车位分配模型在牺牲较小的停车收益、时空资源利用率以及停车请求接受率的同时可以获得较大的可持续利用性的提升，从长远考虑，较高的可持续利用性可以更好地应对停车需求的不确定性，最终实现更高的时空资源利用率。本文的研究可以为实践中的动态化车位分配提供理论支撑，对提高城市停车位的时空资源利用率有着重要意义。

Abstract: To increase the utilization of the urban parking slots, based on the real-time status of sharing parking slots of one single parking lot, this article collects information of parking requests dy-namically, and establishes a two-stage dynamic sharing parking slots allocation model with objective of maximizing the spatiotemporal resource’s sustainable utilization of parking slots and consideration of the parking revenue to make decisions on parking requests and allocate a parking slot for every accepted parking request. The model can be solved through the implicit enumeration method. Analysis of examples shows that compared to traditional first-come-first-served allocation method, the proposed two-stage dynamic sharing parking slots allocation model can increase the resources sustainable utilization a lot while decreasing the parking revenue, the utilization of parking slots and the acceptance rate of parking requests a little bit. And, while taking the long view, the high sustainable utilization of resources can be beneficial to facing the uncertainty of parking requests so that the final spatiotemporal resources utilization of parking slots will be much higher. The research can provide theoretical support for dynamic sharing parking slots allocation in practice, and it is of great significance to improving the utilization of spatiotemporal resources of urban parking spaces.

1. 引言

随着经济的不断发展，中国人均汽车保有量在逐年增加。根据2018年上海市国民经济和社会发展统计公报，2018年年末全市私人汽车数量已达302.17万辆，较2017年增长10.1% [1]。汽车数量的急剧增长直接导致了停车难的问题，进而产生了更大的环境污染和交通拥堵。

为解决停车难问题，很多学者提出了共享停车的方式，此概念产生于20世纪80年代的美国 [2]，近40年来诸多学者针对停车位共享展开了大量研究，主要分为三个方面：共享停车位的可行性研究 [3] [4] [5]、用户停车选择行为和车位需求预测研究 [6] - [12] 以及共享停车请求决策和车位分配模型的研究 [13] - [20]。在对单停车场的车位分配问题研究方面，Dušan Teodorović和Panta Lučić [13]以停车场管理方收益最大化为目标建立模型动态地对用户的停车请求做出接受与否的决策。Shao等人 [14] 针对单停车场以收益最大化和停车拒绝损失最小化为目标提出了一种共享停车预定和车位分配模型。Yanfeng Geng等人 [15] 针对单停车场以用户停车价值最大化(包括停车质量和停车费用)为目标提出了一种基于停车位资源分配和储存的共享车位分配系统模型，模型在每次计算时会将待分配和已分配但未使用的停车请求统筹分配以使目标更优。林小围等人 [16] 以停车场使用效率最大化为目标建立了共享私家车位动态预约和分配模型，并提出提前获知车位供给信息对提高停车场使用效率有很大帮助。张文会等人 [17] 基于单停车场和非动态化信息建立了以停车位利用率最大化和用户停车后步行距离最小化为目标的双目标停车位分配模型。孙琢 [18] 指出停车场时空利用率低是用户的停车请求时段不能被完全覆盖、车位分配产生过多时间碎片以及热点时间段的时间碎片过多导致的，因此，他提出了一种多模式车位预约实时匹配算法，利用多模式预约策略细化用户需求以减少用户退订或反复预约，同时利用时间碎片检测算法和时间重要度检测算法评估车位可持续利用的能力。Jingwei Yu等人 [19] 以停车场收益最大化为目标，基于大商场的停车场提出了夜间车位共享的整数线性规划模型。Qinggang Wang等人 [20] 将停车位视为一个二维的停车资源池(包含时间和空间)，以不连续停车资源最小化为目标建立动态车位分配的整数规划模型，并采用停车资源空置率、停车资源沉没率、停车需求满意率等指标进行评价。

关于单停车场共享车位分配的研究为共享停车的发展提供了理论基础，大多数研究都假设停车请求数据和车位共享数据可以提前获得，而在实践中，停车请求数据往往不可提前获知，此时基于停车请求数据和车位共享数据已知建立的车位分配模型便不再适用。故本文假设一个对外共享车位的停车场，其最初的空闲车位数据是已知的，未来即将在此停车的具体需求数据(车辆数量、到达时间、停车时间)是未知的，在此基础上，本文将以停车场时空资源可持续利用性最大化为目标，同时考虑停车场的收益，建立两阶段动态化车位分配模型，以期降低前序车位分配对后序车位分配的不利影响，从而使最终的分配结果更优。

2. 模型功能说明

本文建立的两阶段动态化车位分配模型包含停车请求决策模型和车位分配模型。停车请求决策模型用于车主发出停车请求时做出是否接受该请求的决策，车位分配模型用于为已接受的停车请求分配具体的车位，模型在整个共享停车流程中的功能如图1所示。

Figure 1. Sharing parking system

图1. 共享停车流程

3. 模型建立

3.1. 模型概念说明

模型以停车场时空资源可持续利用性最大化为目标，同时考虑停车场的收益：停车场时空资源可持续利用性包含车位分配产生的碎片时间的碎片化程度和时间重要度两个概念，停车场收益即是指停车费收入，各概念具体含义如下。

3.1.1. 时间碎片化程度

由于停车时间的随机性，可能会将共享车位的某个空闲时段分割为多个较短且不连续的时间段，即碎片化。例如，一个车位在10点到15点间有5 h的完整空闲时间，当停车请求占用11点至14点的时段时，就会产生两个时长为1 h的时间段，这些较短的时间段被再次利用的概率较低，因为很可能无法满足用户停车需求。类似的碎片时间过多会导致大量空闲时间段无法被利用，从而造成车位资源浪费。空闲时间段的长度可以用时间碎片化程度来表征，孙琢 [18] 给出了时间碎片化程度的计算方式：通过对停车场停车数据进行采集分析，得到车辆停车时长的分布，记频率最高的停车时长为 $T_{\max }$，则碎片时间T的时间碎片化程度为：

$f\left(T\right)=T_{\max }/T$ (1)

其中， $f\left(T\right)$ 表示碎片时间的碎片化程度；T表示该碎片时间的长度(h)。由式(1)可知，碎片时间越长，时间碎片化程度越低，反之越高。

3.1.2. 时间重要度

高峰时刻的车位资源比平峰时刻更加珍贵，这就是时间重要度的概念。车位分配时除了尽可能降低产生的碎片时间的碎片化程度以外，还应使时间碎片尽可能远离高峰时刻，即时间碎片的时间重要度尽可能低，以降低危害。时间重要度可通过以下方式计算：将一天24 h划分为96个时长15 min的时间段，收集停车场在各时间段的停车位使用数量，则各时间段的时间重要度 $g\left(t\right)$ 为：

$g\left(t\right)=a\left(t\right)/a_{\max }$ (2)

式中 $g\left(t\right)$ 表示时间段t的时间重要度； $a\left(t\right)$ 表示时间段t的停车位使用数量； $a_{\max }$ 表示最大的停车位使用数量。

3.1.3. 停车场收益

本研究假设停车费只与停车时间有关，高峰时刻的停车费高于平峰时刻，而避免车位资源浪费，很重要一部分是要避免高峰时刻的车位资源闲置，故停车场收益越高对资源的浪费就会越小。本文假设停车费率与时间的重要度呈正比，则某时段的停车费率为：

$w\left(t\right)=c\cdot g\left(t\right)$ (3)

式中， $w\left(t\right)$ 表示某一时间段t的停车费率(元/h)，c表示高峰时段的停车费率(元/h)， $g\left(t\right)$ 表示时间段t的时间重要度。

3.2. 模型的建立

3.2.1. 请求决策模型

本研究假设停车场共享时间为08:00~20:00，以15 min长的时间段作为时间度量的最小颗粒度，将12小时分为48个时间段，用 $t\left(t=1,2,3,\cdots ,48\right)$ 表示，时间段t对应的时间为： $8:00+(t-1)\times 15\min$ 至 $8:00+t\times 15\min$。用户在提交停车请求时需要输入停车的开始时间段(st)和结束时间段(et)，预约成功后只需在预定的时间段进入和离开停车场即可。

基于以上假设，建立停车请求决策模型如下：

$\max {\displaystyle \underset{n=1,2,\cdots ,N}{\sum }{x}_{jn}\left({\displaystyle \underset{t=1,2,\cdots ,48}{\sum }{q}_{jt}\cdot w\left(t\right)-{\displaystyle \underset{碎片时间}{\sum }w\left(t\right)}}\right)}$ (4)

s.t.

${\displaystyle \underset{n=1}{\overset{N}{\sum }}{x}_{jn}\le 1}$ (5.1)

$a_{nt}+q_{jt}{x}_{jn}\le 1,t=1,2,\cdots ,48,n=1,2,\cdots ,N$ (5.2)

$x_{jn}\in \left\{0,1\right\},n=1,2,\cdots ,N$ (5.3)

$T=0,f\left(t\right)\le 阈值$ (5.4)

式(4)中：

1) n表示车位编号， $n=1,2,\cdots ,N$ ；

2) $x_{jn}=\{\begin{array}{ll}1,\hfill & 第j个请求被分配到车位n\hfill \\ 0,\hfill & 第j个请求未被分配到车位n\hfill \end{array}$，为决策变量；

3) t表示时间段；

4) $q_{jt}=\{\begin{array}{ll}1,\hfill & 第j个请求需要占用t时段\hfill \\ 0,\hfill & 第j个请求不需要占用t时段\hfill \end{array}$，表示第j个停车请求 $q_j=\left(q_{j1},q_{j2},\cdots ,q_{j48}\right)$ 是否需要占用时间段t；

5) 碎片时间指某一车位接受停车请求 $q_j$ 后产生的碎片时间。

式(5)中：

约束(5.1)表示请求 $q_j$ 最多只能被一个车位接受；

约束(5.2)表示同一个车位在同一时间段只能被一辆车占用，其中， $a_{nt}=\{\begin{array}{ll}1,\hfill & 第t时段已被占用\hfill \\ 0,\hfill & 第t时段未被占用\hfill \end{array}$，表示车位的被占用状态；

约束(5.3)表示决策变量为0~1变量；

约束(5.4)表示当接受某一请求产生的碎片时间的时间碎片化程度不大于给定阈值时，认为不会对车位时空资源的可持续利用造成影响，可以接受该请求。

3.2.2. 车位分配模型

成功预约停车的用户会在其预定的开始时间段到达，同一时间段还会有多辆车到达，系统时间段的开始时刻为所有即将驶入的车辆分配车位，车位分配模型如下：

$\min {\alpha }_1{\displaystyle \underset{时间碎片}{\sum }f\left(T\right)}+{\alpha }_2{\displaystyle \underset{时间碎片}{\sum }g\left(t\right)}$ (6)

s.t.

${\displaystyle \underset{n=1}{\overset{N}{\sum }}{x}_{jn}=1,}j=1,2,\cdots ,J$ (7.1)

$a_{nt}+{\displaystyle \underset{j=1}{\overset{J}{\sum }}{q}_{jt}{x}_{jn}\le 1},t=1,2,\cdots ,48,n=1,2,\cdots ,N$ (7.2)

$x_{jn}\in \left\{0,1\right\},j=1,2,\cdots ,J,n=1,2,\cdots ,N$ (7.3)

公式(6)中：

${\alpha }_1$， ${\alpha }_2$ 分别为碎片化程度和时间重要度的权重值，需满足 ${\alpha }_1+{\alpha }_2=1$ ； $f\left(T\right)$， $g\left(t\right)$ 分别为时间碎片的碎片化程度和时间重要度值。

公式(7)中：

约束(7.1)表示每个请求能且只能被分配给一个车位；

约束(7.2)表示车位n的空闲时段t最多只能被一辆车占用；

约束(7.3)表示决策变量为0~1变量。

4. 模型求解与算例分析

4.1. 模型求解

请求决策模型是线性0~1规划模型，车位分配模型是非线性0~1规划模型，本文采用隐枚举法对模型进行求解。

4.1.1. 算法一、停车请求决策模型的求解算法

4.1.2. 算法二、车位分配模型的求解算法

4.2. 算例分析

本研究采用kaggle网站上吉隆坡会议中心的停车场实时停车可用性数据进行算例分析，并对车位分配模型中的碎片化程度和时间重要度的权重 ${\alpha }_1$ 、 ${\alpha }_2$ 做进一步研究。

经过对数据的清洗和处理，得到停车场不同时间段的时间重要度、50个共享车位的初始状态数据、212条停车请求数据。此外，研究采用孙琢在《多模式车位预约实时匹配算法研究》 [18] 中提出的时间碎片化程度计算公式：

$f\left(T\right)=3/T$ (8)

其中 $f\left(T\right)$ 为时间碎片化程度，T为某碎片时间的时间长度(单位h)，多个时间碎片的碎片化程度用如下方式：

$f_{1+2+\cdots +t}=f_1+f_2+\cdots +f_t$ (9)

设高峰时段的停车费率 $c=1$，因为时间碎片化程度的阈值会影响请求决策结果，故首先分析可接受停车请求数与时间碎片化程度阈值之间的关系。利用决策模型求解得二者间关系如下图2：

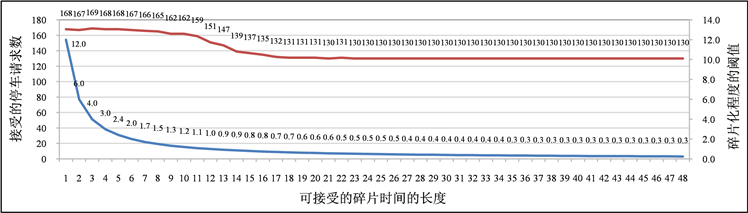
Figure 2. Relationship between parking request decision results and time fragmentation threshold

图2. 停车请求决策结果与时间碎片化程度阈值间的关系

由图2可知，当时间碎片化程度的阈值大于1.5时，可接受的停车请求数随着阈值的减小而急剧减小；当阈值小于1.5时，可接受的停车请求数变化较小；当阈值小于0.7时，可接受的停车请求数趋于稳定。

继续对不同碎片化程度阈值下的车位分配结果进行分析，令碎片化程度和时间重要度的权重分别取不同值，利用车位分配模型进行求解。由于时空资源利用率和停车收益仅与决策结果有关，与分配结果无关，故不受碎片化程度权重的影响，其随碎片化程度阈值的变化如表1：

Table 1. Change of the spatio-temporal resource utilization and parking revenue as the fragmentation threshold changes

表1. 时空资源利用率和停车收益随碎片化程度阈值的变化

注：车位时空资源利用率 = 已利用的时空资源/总可利用的时空资源。

由表1可知，当碎片化程度阈值为1.5时，车位时空资源利用率和停车收益均可达到最大值，且根据图2可知，碎片化程度阈值大于1.5时，可接受的停车请求数方随着阈值减小而急剧减小，故本研究取碎片化程度阈值为1.5。在此阈值下，当时间碎片化程度的权重和时间重要度的权重分别取不同值时，车位分配产生的时间碎片的碎片化程度和时间重要度如表2：

Table 2. Benefits of parking space allocation as α1 and α2 varies

表2. 不同α₁、α₂对应的车位分配效益

注：表中各值为所有请求都已被分配车位后的结果。

由表2可知，当 ${\alpha }_1=0.7$， ${\alpha }_2=0.3$ 时，结果是最优的，故在后续分析中取 ${\alpha }_1=0.7$， ${\alpha }_2=0.3$。将两阶段车位分配模型的分配效益与决策阶段初步分配的效益以及先到先得传统分配方式的分配效益进行对比，结果如表3：

Table 3. Comparison of benefits of three distribution modes

表3. 三种分配方式的效益对比

由表3可知，两阶段分配模型的效益优于决策阶段初步分配的结果，当与传统先到先得分配方式对比时，两阶段分配模型的允许停车数(降低3.51%)、车位时空资源利用率(降低1.05%)、停车收益(降低1.05%)均有所下降，但剩余可用时间的碎片化程度降低了31.67%，且剩余可用时间的时间重要度几乎不变，这表明车位的可持续利用性有了较大提高。

根据以上数据，我们可以发现两阶段动态化车位分配模型在现时情况下无法提高停车收益、时空资源利用率以及停车请求的接受率，但却可以显著提高停车位时空资源的可持续利用性，从长远考虑，较高的可持续利用性可以更好地应对停车需求的不确定性，最终实现更高的时空资源利用率。

5. 结论

本文提出的两阶段动态化车位分配模型包括停车请求决策模型和车位分配模型。算例分析表明，相比传统先到先得的车位分配方式，本文提出的模型在牺牲较小的停车收益、时空资源利用率以及停车请求接受率的同时可以获得较大的可持续利用性的提升，从长远考虑，较高的可持续利用性可以更好地应对停车需求的不确定性，最终实现更高的时空资源利用率。后续研究可对车位分配模型的求解算法做进一步优化，并可以将研究对象从单停车场扩展至区域内多停车场。