交通拥堵形态的聚类判别实现

The Clustering and Discrimination of Traffic Congestion Form Is Realized

摘要: 城市道路中司机对路况全貌不了解，极有可能驶入拥堵路段耽误行程，预知实时路况可以避开拥堵路段尽快到达目的地。驾驶过程需要观察前方，因此语音播报成为必须，但逐条路段播报不利于司机掌握全貌且播报不及时，本文通过聚类分析方法，对路网中的拥堵分布给予高度归纳概括、准确的信息表达，从而使得机器自动识别并在有限时间内语言推送表达信息，避免对司机形成信息干扰。有利于司机有限时段内掌握前方路况全貌。

Abstract: Drivers don’t know the full picture of road conditions in the urban road network, so it is very likely to delay the journey when driving into the congested road sections. Predicting the real-time road conditions can avoid the congested road sections and reach the destination as soon as possible. In the driving process, it is necessary to observe the front, so voice broadcast is necessary, but it is not conducive to the driver’s grasp of the whole picture and the broadcast is not timely enough. In this paper, through clustering analysis method, the congestion distribution in the road network is highly summarized and accurately expressed, so that the machine can automatically recognize and push the expression information in a limited time, avoiding the formation of information for the driver Interference. It is beneficial for the driver to master the full view of the road ahead in a limited period of time.

1. 引言

随着城市化进程的加速，城市交通拥堵成为了常见现象，司机行驶中对路况全貌不易了解，极有可能驶入拥堵路段耽误行程，且对于交通管理来说，大量不明路况车辆陆续涌入拥堵加剧，增加了交通疏散难度。因此对于司机来说，预知实时路况可以避开拥堵路段尽快到达目的地，提高通行效率。

国内有不少学者研究交通拥堵，兰州交通大学的刁爱霞 [1] 分析了兰州市交通拥堵现状，然后解析了导致其交通拥堵原因，根据兰州市交通的具体情况给出相应的缓解拥堵的措施，如优先发展公共交通系统、实施交通需求管理、大力发展智能交通系统等。牛凯 [2] 通过寻求城市交通拥堵预测判别方法，从人为、车辆、道路、环境4方面提取出6个造成交通拥堵的关键因素，采用BP神经网络建立城市交通拥堵预测模型，通过案例分析验证了模型的准确度。袁浩 [3] 为了揭示城市建成环境对交通拥堵状态影响的空间异质性，以西安中心城区街道为基本研究单元，采用拥堵延时指数表示交通拥堵状态，基于多源数据构建地理加权回归模型进行实证研究。韦清波 [4] 在分析城市道路交通拥堵指数总体变化规律的基础上，综合考虑天气、节假日、重大活动等因素对交通的影响。刘张 [5] 提出了一种添加调节项的高阶多变量马尔可夫模型(AAT-HO3M)，证明了模型的收敛性，进行了参数估计，并参考城市道路交通运行评价指标体系，对城市拥堵进行预测分析。晏雨婵 [6] 针对各交通时段对交通拥堵的不同影响、单因素无法准确表征交通拥堵状态的问题，提出了一种采用多指标模糊综合评价的交通拥堵评价预测方法。姚志洪 [7] 发现了与经典的Robertson车队离散模型相比，动态异质交通流车队离散模型对下游交叉口的到达车辆流量分布预测效果更好，平均预测均方根误差可减少26.51%。陈清元 [8] 利用最小方差法搜索变点，建立了基于交通流平稳性突变的交通事件检测算法，最后通过VISSIM仿真实验验证该算法的有效性。杨连坤 [9] 通过卷积长短期记忆网络对时空信息及交通模式相似信息进行特征捕捉用于交通速度预测，之后根据预测速度与路段自由流速度的关系计算交通指数并评估未来交通状态变化。实验验证了预测模型在速度预测与交通状态估计上的有效性。邹延权 [10] 选取深圳市作为研究对象，以浮动车GPS数据、土地利用数据和路网数据为基础，将深圳全市划分为1031个交通小区，分别使用全局回归模型、空间Durbin模型和变尺度GWR模型来量化分析城市建成环境对O-D时空分布的影响。

目前较为有效的手段有关注交通广播的路况播报和运用导航软件设定开启目的地导航。交通广播是针对全市范围的路况播报且时间有限，并不针对每个司机个体当前位置提供信息，对具体司机的路况指引服务是有限的；车载导航系统是考虑路况后为司机提供最优路径。然而，多数城市驾驶为熟悉型出行，即上下班、上学放学、到常去的购物消费场所等，由于嫌麻烦或熟悉目的地等原因基本上不会开启导航服务，因此无法得知前方路况信息。车载装置语音播报是一种新的诱导形式，为方便用户无需开启导航，系统自动伺服侦听当前位置，下载路况数据，在车辆临近交叉口转向选择时，将前方路况播报给司机，使其提前知道前方路况，及时避免驶入拥堵区域，可有效缓解拥堵压力。

但是，司机关注的往往前方一定区域范围内的路况，而拥堵时标定在每个路段上的，范围内路段众多，车辆临近交叉口很短时间内全部播报，根本来不及，另一方面，分路段的零散信息使司机无法掌握整体路况，故而需要对前方路况做一个高度归纳概括，即进行路况的形态识别(图1)，从而在短时间内快速播报前方路况整体全貌。

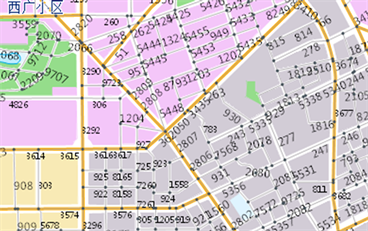
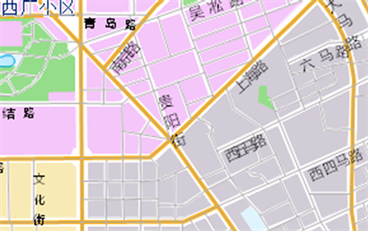注：整体概括表述比分路段表述更简洁且获得整体性，此时路段用的编号示意

Figure 1. Section is summarized as the overall description

图1. 路段归并为整体描述示意

2. 拥堵形态的人工智能判别

2.1. 拥堵形态分类与特征描述

本文分析认为城市内部的拥堵在形态上可表述为“点、线、面”三种形态。

1) 节点性拥堵

由于道路为线性结构，因此拥堵的基本形态也是呈线性展开，但拥堵长度较小时，往往表述为在某个点上发生拥堵，如：某某路某处局部性拥堵、某某交叉口拥堵。

2) 线性拥堵

节点拥堵长度达到一定量值时，可称为线性拥堵，在语音播报时根据拥堵在整条道路中的分布，可分为间断性拥堵、一端拥堵、全程拥堵等形式。表述为：某某路在某处–某处拥堵，如：中山北路山西路到鼓楼段拥堵或某某路某处有多长的拥堵。

3) 区域性拥堵

拥堵分布于相互关联的路段且形成一定团状规模，实质是多个道路拥堵形成拥堵网络，但语音播报时，用网络比较抽象，故而称为区域性拥堵。区域范围及内含的点和线有一定数量标准。表述时，以组团中地标称谓，如某大厦周边2公里范围内区域拥堵。

2.2. 基于聚类分析归并拥堵形态

驾驶过程中为安全起见，司机不可能时刻紧盯地图人工识别拥堵现状，本文考虑通过人工智能聚类分析将相同和相近拥堵段归并为整体形态，以利于后续根据标准，判定拥堵形态，即由机器自动识别概括电子地图上的拥堵状态语音推送给司机。

聚类是通过函数算法的形式提取相似对象的过程。本文为了将对象聚类归并，需要将数据对象划分为若干组，通过函数计算出每一个对象之间的距离，对象之间的距离表明它们是否相似，同组属性类似的对象组合，并将其看作一个对象。

2.2.1. 基于Q型聚类测段分解

聚类分析一般分为Q型聚类和R型聚类，Q型聚类分析主要是针对已经观测到的数据进行聚类分析，将相似的一类分组，而R型聚类分析是针对较多变量时通过降维的方法进行聚类分析。本文主要对测点路段的拥堵程度的不同进行聚类，属于观测数据，较适合使用Q型聚类分析。

Figure 2. Cluster analysis and regression results of the road test sections

图2. 道路测段聚类归并示意

基于对数据聚类的考虑，本文首先是将路段按一定步长分解为若干测段，形成由众多测段组成的道路网络。各测段内的拥堵程度(按照交通部交规院标准分为五级拥堵描述)成为聚类的基本元素(图2)。

2.2.2. 聚类相关参数选择

鉴于聚类分析是依次合并的过程，规定类间距离和类内各数据的距离，让n个参数各为一类，开始时，因每个样本为一类，类间距离与类中距离相等；然后，将距离最近的两个类合并；如此重复，每个循环将减少一个类，直至所有的样本归为一类为止。但是将所有的数据归成一个类别并不是实验所需要的结果，因此，当聚类方法迭代到某一程度就需要停止计算，获得有意义的聚类结果，需要合理选择聚类分析方法。

通过各类聚类方法的对比分析，本文认为改进主成分法具备了一系列聚类算法的优点，其运用均值化的标准化方法，将标准化的变量进行主成分分析，提取主成分，再进行聚类分析，其优点是可以保持数据的真实性，并且通过降维减少计算量。鉴于改进后因为某些变量具有相关性，可提高分类的精准度且符合本本文面对问题，本文将选用其中的K-均值聚类方法，此方法是发现给定的数据集的k个簇的算法，每个簇通过质心，即簇中所有点的中心来描述。数据 $\stackrel{\rightharpoonup }{x_i}$ 和 $\stackrel{\rightharpoonup }{x_j}$ 之间的距离为 $d_{ij}$，距离越小表示他们之间越相似，在方法中采用欧式距离平方计算对象之间的距离，采用最短距离法计算K-均值聚类的类别距离。

欧氏距离 $d_{ij}=\sqrt{{\displaystyle \underset{k=1}{\overset{p}{\sum }}{\left(x_{ik}-x_{jk}\right)}^2}}$。

2.2.3. 算法流程

K-均值聚类支持函数算法主要有以下几个函数，第一个loadDataSet()，此函数方法是将数据导入算法中，并将数据存入dM矩阵中，第二个distEclud()，用来计算计算欧式距离，最后一个randCent()，该函数主要是建立一个集合去存放产生的随机质心，并构建算法使用的数据集。关于质心的选取必须要数据集的范围之内，因此可以通过查找每一个数据集的边界大小来完成此项工作。

在上述函数搭建完成后，本文建立完整的k-均值算法。首先，随机确定k个初始点(本文中为测段)作为质心。然后将数据集中的每个点分配到一个簇中，为每个点找距离其最近的质心，并将其分配给该质心所对应的簇。这一步完成后，每个簇的质心更新为该簇的所有点的平均值，迭代计算。迭代次数取决于数据点的分配计算是否还在变动。流程图如图3所示。

将测段拥堵值作为参数传入kMeans()函数。然后按照上述算法反复迭代。为了判断是否迭代需要设置变量ca(主要用于判断赋值)，如果该值输出为Ture，则继续迭代。上述迭代过程通过使用循环来实现。最后，程序会返回所有的类质心与分配结果并给出聚类结果，得出测点拥堵值的聚并归类。

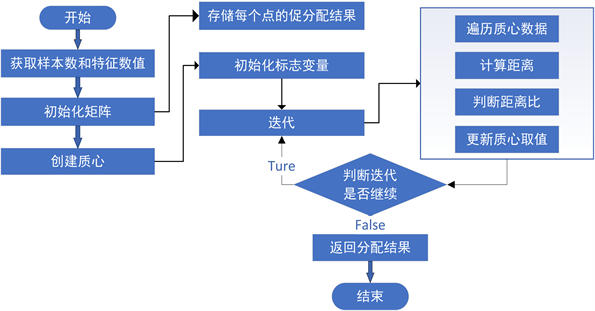
Figure 3. K-mean clustering algorithm flow

图3. K-均值聚类算法流程

2.3. 基于回归算法识别拥堵形态

聚类归并完成后，需要依据标准机器判别拥堵形态，对于确定点、线、面形态的标准，目前学术界并没有明确的界定，本文通过调查问卷、专家打分结合的方式加以确定，本处重点在于给出基于标准进行判别的方法，通过Logistic回归实现。

Logistic回归的一般过程为收集数据，准备数据，分析数据，训练算法，测试算法，使用算法。要使Logistic回归能接受所有的输入然后预测出分类结果，需要使用海维塞德阶跃函数(Heaviside step function)，但是该函数从0到1时间过快，因此过程非常难处理。但是经过研究发现Sigmoid函数具有海维塞德阶跃函数类似性质，并且在跳跃时更容易处理，因此选用Sigmoid函数。

2.3.1. 确定回归系数

因为在使用Logistic回归算法时需要确定每个样本的回归系数，本文采用基于最优化方法的即梯度上升法确定最佳系数。流程图如图4所示：

Figure 4. Gradient ascending flow

图4. 梯度上升流程

然后通过分析数据，找出决策边界，最后通过测试进行Logistic回归进行分类。

2.3.2. 设定Sigmoid函数

根据上文所述已经将近似路段归并聚类，对拥堵形态的判别时采用基于Logistic回归和Sigmoid函数分类。Sigmoid函数设计如下：

$\sigma \left(z\right)=\frac{1}{1+{\text{e}}^{-z}}$ (1)

将此函数的输入记为z，则表示如下：

$z=w_0{x}_0+w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n$ (2)

上述公式为线型方程的形式，其向量形式可以写成 $z=w^{T}x$。其中向量x是分类器的输入数据，向量w也就是本文要找的最佳分类参数。此算法主要的思想是找到某个函数曲线中的最大值，最佳路径即为

梯度变化的方向。可以通过 $\nabla f\left(x,y\right)=\left(\begin{array}{c}\frac{\partial f\left(x,y\right)}{\partial x}\\ \frac{\partial f\left(x,y\right)}{\partial y}\end{array}\right)$ 来求得函数梯度值。若算子移动的步长记作 $\alpha$，则梯度上升算法的迭代公式如下：

$w:=w+\alpha {\nabla }_{w}f\left(w\right)$ (3)

2.3.3. 算法流程

在计算分类边界时将上述的问卷调查结果作为一个系数矩阵传入算法。最后对交通拥堵形态进行Logistic回归分类，其决策边界程序流程如图5所示，分类函数程序流程如图6所示：

Figure 5. Decision boundary flow

图5. 决策边界流程

图6中colic_test()，是将数据进行格式化处理函数。数据初始化有三个标签“点”、“线”、“面”，数据导入之后，对数据集进行迭代。最后通过此分类算法将“点”、“线”、“面”判别出来。

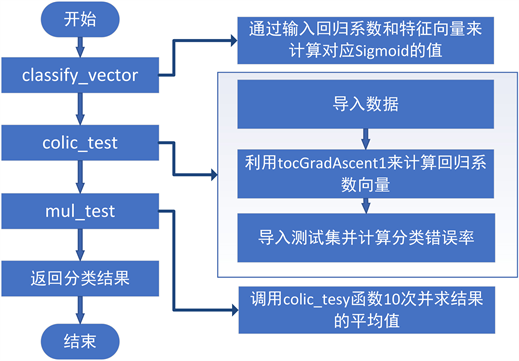
Figure 6. The Logistic regression classification process

图6. Logistic回归分类流程

3. 算例分析

3.1. 实验过程

在通常情况下，“点”、“线”、“面”这三种基本组成类型体现了市域交通拥堵的空间分布，需要实时获取发生交通拥堵的地点以及信息，并且将其呈现在路网结构上且传入到数据库中，本文爬取高德地图的拥堵道路数据进行拥堵形态分析。对数据库中的数据进行计算来判断发生交通拥堵形态，将基于Logistic回归和Sigmoid函数分类算法改写为java语言嵌入到地图API中去做二次开发。

3.2. 测试结果

3.2.1. 聚类实验

本文选取南京市北京西路设置20个测段进行举例实验，获取测点数据作为输入样本将其带入基于排序指标的拥堵测度模型中计算的拥堵值如表1所示：

Table 1. Congestion value data

表1. 拥堵值数据

将拥堵值传入放入datMat中，因为算法将用于Android系统中，因此本文将算法改写为java语言(程序核心为附录四)执行对道路进行具并归类结果如下：

从数据中可以发现测点3的数据并不是畅通，以及测点15是非常拥堵，经过K-均值聚类算法近似测段聚类归并后的结果符合预期结果。

3.2.2. 形态识别

本文选取南京市南部区域进行分析，多次行驶不同路况的路网皆可以准确的判别出车辆前方的拥堵形态，下面列出典型测试实验结果如下：

系统对于拥堵形态的判断结果，如图7的图7(a)、图7(b)、图7(c)。图7(a)中行驶区域都为畅行，仅交叉口由南向北100米为为轻微拥堵，系统将其拥堵形态判断为“节点性拥堵”，表述为雨花南路与共青团路交叉口由南向北发生节点性拥堵。

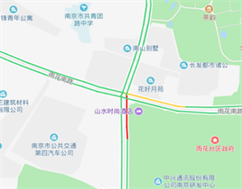(a) 节点拥堵 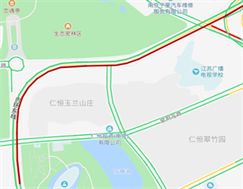(b) 线性拥堵 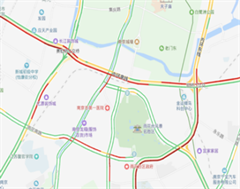(c)区域拥堵

Figure 7. Congestion clustering and morphological analysis

图7. 拥堵聚类与形态分析

图7(b)中识别出了全线拥堵，由于本段路拥堵性质较均匀，较易被聚类算法所识别，表述为内环东西自科技宫至广播电视学校段发生较严重线性拥堵。

图7(c)中，不仅识别出了内环南线双向的全线拥堵，并且因为附近的几条道同样出现不同程度的拥堵，并且有3个以上的交叉口参与达到定性为区域性拥堵标准，算法将其分类为“区域性拥堵”。表述为雨花台公园周边3公里多条路段发生区域性拥堵。需要说明的是，区域北侧道路为严重拥堵和中度拥堵相间的非均匀状态，算法通过聚类分析确定为整体线性拥堵。

4. 结论

本文首先梳理了城市道路中拥堵形态的分类并分析其特征和表述方式；针对车辆了解前方路况过程中遇到的信息众多难以即使播报的问题，采用基于Q型聚类方法进行拥堵形态的分析，归并前方复杂路段信息；基于回归算法进行拥堵形态的识别，对路网中的拥堵分布给予高度归纳概括、准确的信息表达，从而使得机器自动识别并在有限时间内语言推送表达信息，避免对司机形成信息干扰。通过算例分析测试能有效识别拥堵形态并在有限时间通知司机，起到了良好的效果，有利于司机有限时段内掌握前方路况全貌。

文中对于判断点线面的标准是否合理未予展开讨论，重点讨论聚类方法以及基于标准的人工智能判别方法，根据聚类归纳出的各形状对象，采用基于Logistic回归和Sigmoid函数分类算法在问卷调查数据形成标准的基础上进行分类，做出决策边界。

基金项目

本项目受无锡市住建局科技计划“基于LBS的被动式行车路况预报装置研究”资助。