基于Hopfield神经网络模型的验证码识别问题

Hopfield Neural Network Based Approach to Recognizing the Verification Code

摘要: 为了避免恶意破解密码、刷票、论坛注水、黑客攻击等行为，验证码因此而生，它通过强制人机交互的方法来抵御机器自动化攻击。但准确识别验证码是当前还未完全解决的难题。本文的研究对象为四位数字的验证码，采用分割分析和Hopfield神经网络的方法对验证码识别及其精度进行分析。建立并训练Hopfield网络对验证码图像变换后的矢量进行模式识别，比对的结论表明，Hopfield神经网络算法可以得到比较好的测试结果，具有推广应用的价值。

Abstract: In order to avoid malicious cracking of passwords, ticket brushing, forum water injection, hacking, etc., verification codes are born. It uses the method of forcing human-computer interaction to resist machine automation attacks. But accurately identifying the verification code is a difficult problem that has not yet been completely resolved. The research object of this article is a four-digit verification code. The method of segmentation analysis and Hopfield neural network is used to analyze the verification code recognition and its accuracy. Establish and train the Hopfield network to perform pattern recognition on the transformed vector of the captcha image. The conclusion of the comparison shows that the Hopfield neural network algorithm can get better test results and has the value of popularization and application.

1. 引言

图像识别问题是人工智能领域上一个复杂的问题，其本质是图像被计算机分析和处理，对于不同种类的图像处理方式也会有所不同，是一种被开发出识别各种模式的目标和对象的技术。图像识别的种类繁多，验证码识别是其中一种，也是互联网上常用的真实人机交互验证的有效方法 [1] [2]。

对于识别数字验证码这个问题，国内外众多学者进行了许多研究，李成建等 [3] 在识别数字验证码问题上使用了卷积神经网络算法；潘浩等 [4] 利用Tesseract引擎，在经过训练之后，能够分别识别简单和复杂的验证码；冯军军等 [5] 提出了一种多模块验证码识别方法，这种方法涉及python3、selenium、PIL等模块。但是这些算法着重研究模块化识别，考虑到常用的验证码有四位数字和字母验证码以及目前最新的汉字验证码，本文主要考察的验证码是由四位数字以及一些噪声组成的图片。本文先对数字验证码使用了如下预处理操作：灰度化、二值化和边缘检测分割。再通过中值滤波的方法去除噪点，将图片转变成Hopfield神经网络进行模式识别。这么做具有一定的抗干扰能力是因为其结合了神经网络的联想记忆功能。图形用户界面(GUI)测试结果表明，Hopfield神经网络模型具有良好的稳健性。

2. 图像的预处理

如图1，验证码为带噪声的数字，计算机无法直接识别和处理带有太多噪声的验证码，因此，就需要预处理验证码，首先将每个图像中的四个数字全部转化为单独分开的数字，再利用归一化把每个数字转为7*5的二值图像，然后根据灰度值把图像转化成维数为35的向量，最后把向量放入Hopfield网络进行识别。

Figure 1. Digital verification code

图1. 数字验证码

2.1. 灰度化

在对数字验证码图像做识别研究的过程中，如果想要让计算机更快速和有效的识别数字验证码图像，有一个步骤是不可省略的，那就是对彩色图像进行灰度化处理 [6] [7]，阈值分割是灰度化处理的目的。计算阈值有很多的方法，本文考虑了最大亮度法，它的计算方法为：

$g\left(i,j\right)=\text{Max}\left(R\left(i,j\right),G\left(i,j\right),B\left(i,j\right)\right)\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}$

验证码图像经过灰度化后的结果如下图2所示：

(a) (b) (c) (d)

Figure 2. Retain the grayscale results of the maximum brightness method

图2. 保留最大亮度法的灰度化结果图

2.2. 二值化

设背景色用0表示，目标像素用1表示。则灰度图的二值化 [8] 可以表示为：

$g\left(i,j\right)=\{\begin{array}{cc}1& f\left(i,j\right)>T\\ 0& f\left(i,j\right)\le T\end{array}$

其中T指的是确定的阀值。

二值化的核心步骤就在于此阀值，本文采用最大类间方差法确定T的取值 [7] [8]。

最大类间方差法是由Otsu在1978年提出的一种算法 [7] [8]，这种算法一经提出就被广泛使用。定义类内方差 ${\sigma }_w^2$，类间方差 ${\sigma }_{\beta }^2$ 和总体方差 ${\sigma }_T^2$，还定义了三个等价的标准度量：

$\lambda =\frac{{\sigma }_{\beta }^2}{{\sigma }_W^2},K=\frac{{\sigma }_T^2}{{\sigma }_W^2},\eta =\frac{{\sigma }_{\beta }^2}{{\sigma }_T^2}$

为了避免过多的计算，通过简化下面的公式进行简化：

${\sigma }^2\left(T\right)=W_A{\left(\mu a-\mu \right)}^2+W_b{\left(\mu b-\mu \right)}^2$

其中， ${\sigma }^2$ 为两类间最大方差， $W_A$， $W_b$ 分别为A，B类概率， $\mu a$， $\mu b$ 为分别为A，B类平均灰度， $\mu$ 为平均灰度。

不同阈值会将图像分割成两个不同的部分，若T能使分成两部分的总方差 ${\sigma }^2\left(T\right)$ 取得最大值，那么该值就是最佳阈值。下图3是对原图利用上述方法后的对比。

Figure 3. Maximum interclass method binarization

图3. 最大类间法二值化

2.3. 中值滤波

噪声是识别数字验证码图像中的一个阻碍，它会大大降低计算机识别的准确性，因此需要对数字图像进行降噪处理。降噪效果的好坏会影响之后的处理，因此根据噪点的特点，本文使用中值滤波的方法去除噪声，主要利用高频噪声，孤立偏差大的特点进行的 [9] [10]。几种常用的识别窗口如下图4所示，窗口的中心与确认识别的像素对齐。

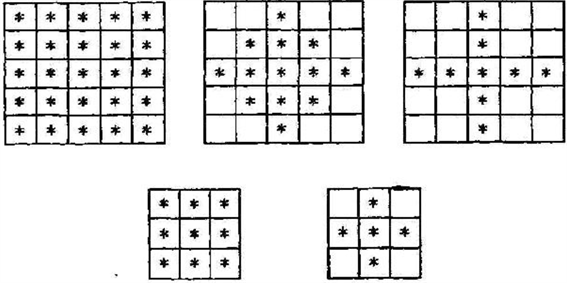
Figure 4. Gray value recognition window

图4. 灰度值识别窗口

本文使用了图4中的3*3模板，过滤结果如图5所示。

从图5可以看出，第二组数字验证码的效果较好，消去了大量的噪点。与之相对比，由于另外三组验证码的噪点不是很多，因此滤波效果不明显，但总体来看，经过中值滤波后的图像上的噪点比未经过滤波图像上的噪点要少，且可以保护图像边缘，因此使用中值滤波效果较好。

Figure 5. Median filter

图5. 中值滤波

2.4. 字符串分割和归一化

神经网络识别的采样要求是单个字符，因此需要分割图像。采用有效的方法能提升识别的准确率。字符串分割的方法有多种，有积分投影法和边缘检测分割法 [9] [10] [11] 等，但利用积分投影法进行字符串的分割时，不同验证码的字符分割位置以及长度和宽度等存在差异，并且不同的字符还可能会相连，难以用简便的算法统一处理。为此，本文构造了基于图像边缘检测的分割方法。

2.4.1. 边缘检测分割法

图像处理中的关键问题是边缘检测，目的是识别图像中光度变化明显的点 [12] [13]。边缘指的是图像中物体与背景之间以及物体与物体之间灰度变化较大的所有点连接起来形成的线，数字图像中物体的边缘可利用灰度的不连续性来寻找，如果将一个边界定义为一组具有一定数量光强变化的点，则边缘检测就是计算光强变化的导数。因此，可以通过使用差分运算来定位对象的边缘，以获得信号的转换率。边缘是两个区域的边界，这是图像分割所依赖的重要定义。这个定义可以用来分割图像。为了解决图像分割问题，就需要识别图像的边缘以便于图像分割。

边缘检测算法的主要思想为：对一个连续的图像 $f\left(x,y\right)$，在位置 $\left(x,y\right)$ 的梯度可以表示成一个矢量，假设用 $G_x$ 和 $G_y$ 来表示 $f\left(x,y\right)$ 沿着x方向和y方向的梯度，对 $G_x$ 和 $G_y$ 分别使用不同模板，然后将两个模板拼在一起，形成梯度算子。对图像使用微分运算，图像灰度变化较小时，计算出的微分值较小。微分值是否边缘点取决于阈值是否小于微分值，如果阈值小于微分值，则将该点定义为边缘点。

本文采用了以Sobel微分算子为基础的边缘检测分割的方法 [12] [14]。

图6是四组验证码图像经过边缘检测后的结果图。

根据图6，我们可以看出，经过边缘检测后的图像与之前的图像相对比少了很多的数据，也能起降噪的作用，并且保留了原图中的重要数据信息。

2.4.2. 归一化

由于Hopfield网络需要输入相同的格式，但切割后的字符大小存在差异，为了让识别的标准性和准确率更高，就需要把图像标准化，统一尺寸。因此需要将切割后的字符图像尺寸归一化为7*5，然后逐行化为长度为35的一维向量P。

Figure 6. Image after edge detection

图6. 边缘检测后的图像

3. Hopfield网络识别模型的建立与验证

3.1. 神经网络的基本原理

Hopfield网络全连接网络 [13]。图7就很好地展示出了一个Hopfield网络，其中 是神经元的数量，V是输入向量，U是输出向量，W是神经元之间的连接权值。在离散Hopfield网络中，是每个神经元仅有“1”与“−1”这两个可输出的状态值。可用向量 $V=\left\{v_1,v_2,\cdots ,v_n\right\}$ 表示当前神经元的状态，其中 $v_i$ 表示第i个神经元的状态。由于神经元两两相连，因此两个不同神经元之间可以相互传递信息。

Figure 7. A fully interconnected network with feedback

图7. 有反馈的全互联型网络

设一个Hopfield网络由n个神经元构成， $V_i$ 和 $V_j$ 分别表示第i，j个神经元节点的状态，W表示神经元i和j的连接权值， $\theta$ 表示神经元i的阈值。那么节点的能量可表示为：

$E_i=-\left(\underset{j\ne 1}{\overset{n}{{\displaystyle \sum }}}{w}_{ij}{v}_i-{\theta }_i\right)v$

因此，网络整体能量的函数表示如下：

$E_i=-\frac{1}{2}\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j\ne i}{\overset{n}{{\displaystyle \sum }}}{w}_{ij}{v}_i{v}_j+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{\theta }_i{v}_i$

设一个Hopfield网络由n个神经元构成的，在t时刻，记第i个神经元接收来自剩下 $n-1$ 个神经元输入值的总和为 $u_i\left(t\right)$。在 $t+1$ 时刻，如果第i个神经元的输出值 $v_i\left(t+1\right)$ 是符号函数作用于 $u_i\left(t\right)$ 中的某个阈值时，则该神经元称为活跃神经元。此迭代步骤为：

步骤1：将i作为随机选择的一个神经元；

步骤2：计算选中神经元 $i\left(1\le i\le n\right)$ 的总输入

$u_i\left(t\right)={\displaystyle {\sum }_{j\ne i}^n{w}_{ij}{v}_i-{\theta }_i}$ ；

步骤3：根据 $u_i\left(t\right)$ 值大小，改变神经元的状态

if $\left(u_i\left(t\right)\right)\ge 0$

then $v_i\left(t+1\right)=1$

else $v_i\left(t+1\right)=0$ ；

步骤4：除神经元i以外的其他神经元j状态不发生改变；

步骤5：转到(1)，循环至网络稳定为止。

Hopfield网络具固定的稳定状态，权矩阵W可以根据网络的学习求得，再利用计算的方法进行联想。对于给出的M个模式，可以使用Hebb规则进行学习。

$W_{ij}=\{\begin{array}{ll}0\hfill & i=j\hfill \\ \underset{k=1}{\overset{M}{{\displaystyle \sum }}}{v}_i\left(k\right)v_j\left(k\right)\hfill & i\ne j\hfill \end{array}$

依照上述的法则求得权矩阵后，就已经把这 个模式存入到网络的连接权中。

3.2. Hopfield神经网络建立

3.2.1. 输入样本的设计

对每个数字图像进行数字化处理，并将数字图像转换为神经网络可以处理的输入值和输出值，这样就得到输入样本。

0~9中的每个数可以用带布尔值的7*5矩阵表示。比如“0”可以表示为：

$r0=\left[\begin{array}{ccccc}0& 0& 1& 0& 0\\ 0& 1& 1& 1& 0\\ 1& 1& 0& 1& 1\\ 1& 0& 0& 0& 1\\ 1& 1& 0& 1& 1\\ 0& 1& 1& 1& 0\\ 0& 0& 1& 0& 0\end{array}\right]$.

每个数字都可以用7*5 = 35个元素组成一个行矩阵，再将10个数字均被定义成输入向量，每个数字的输入向量都有35个元素，全部数字组成一个10*35输入向量矩阵alphabet。把这10个数字输入到变量Number中，变量成为网络的输入样本矩阵：

$\text{Number}=\left[r1,r2,r3,r4,r5,r6,r7,r8,r9,r10\right]$.

3.2.2. 输出样本的设计

输出样本定义为10*10单位矩阵。对于每个数字输入，输出在其行的相应位置为1，在其余位置为0。利用下面的MATLAB命令能简单实现：

Figure 8. The sum of error squares and the change in learning rate

图8. 误差平方和及学习速率的变化图

Targets = eye (10)。

每输入一个数字，网络就可以输出一个向量。

3.2.3. 网络结构的设计

根据上文可知，神经网络需要输入35个神经元和输出10个神经元 [14] [15]。建立BP网络的必要条件是确定隐层和隐层神经元的数目，本文所用的BP网络只有一个隐层，隐层神经元的个数必须经过多次重复实验才能确定一个合适的值，一种比较好的方法就是：每次调试时，为了加快误差下降的速率，只增加1或2个神经元。根据这种方法，经过测试，最终选定10个神经元作为隐含层神经元的数量。

网络接受的输入向量应该为布尔向量，但是实际上，接收到的输入向量并不是布尔向量，这是因为存在一定的误差。为了避免这样的误差给实验带来不便，就需要设计的网络有一定的容错能力。可以设置噪声的均值为0并且标准偏差小于或等于0.2，这样网络就有一定的容错能力辨别输入向量。

把该网络设计成两层的BP网络结果，这样能够识别数字。在隐含层和输入层之间的神经元传递使用logsigmoid函数，这个函数输出的值为布尔值，再将输出的值输入到输入层中。

3.2.4. 初始化

首先生产10个样本数据，让它们每个能代表0~9中的每个数，再构造双层网络，本文使用了newff函数，再定义第一隐含层权值WI和B1初始值，本文采用初始化的nwlog.m函数，用随机数选取后一层的初始值。这便是对hopfield网络的初始化过程。

3.3. 无噪声网络训练

上述设计的网络没有抗干扰的能力，为了使其具备这个能力，就需要对网络进行训练，经过训练的网络能正确的处理由于错误输入导致的问题。如果能得到一个可以识别带有噪声的输入值的网络，就能把干扰噪声数字化处理转换成有均值的随机值。

为了训练一个具有低平方误差和理想输入的网络，本文的无噪声训练采用学习速度快捷、附加动量因子的BP算法 [14] [15]。

图8表现了在网络训练过程中，误差平方和、学习速度在各个学习阶段的变化。从图8中可以看到，网络的稳定性会随着学习次数的增加而提高。从图中还可以看出，在学习次数大约为196次时，我们设计的神经网络会达到稳定状态。

3.4. 网络测试

在网络测试中，通过GUI界面，来提高交互性。得到的测试结果分别如下图9所示。

Figure 9. Test result

图9. 测试结果

4. 小结

验证码的自动识别归根到底是人工智能的问题，这里主要考察数字验证码的识别问题，采用的是Hopfield神经网络与模式识别的研究方法。神经网络模型本身发展并不成熟，一些基础的理论也有待完善，拥有自身固有的优缺点 [16]。由图9可以看出，本模型有一定的识别价值。但是其正确率有待提高，特别是数字验证码识别的难点主要体现在3、5、9身上，因为这些字符特征很相近，再加上一些随机性的干扰，很容易将其误识，这也是符合常理的。另外，在进行网络训练时，应保证对充足的样本来进行训练。对于含噪声的数字样本的识别问题，值得进一步研究。

基金项目

海南省自然科学基金(120RC451)，国家自然科学基金(11761025, 11961018, 11901114)，广东省教育厅青年创新人才类(2017KQNCX081)，广州市科技创新一般项目(201904010010)，中山大学广东省计算科学重点实验室开放课题基金资助(2018001)，海南省研究生创新科研课题项目(Hys2020-108)。

NOTES

^*通讯作者。