基于隐马尔可夫模型的危险跟驰行为识别研究

Identification of Dangerous Car Following Behavior Based on Hidden Markov Model

摘要: 随着汽车智能化发展，碰撞危险预警已成为主动安全技术中的重要研究内容。进行碰撞危险预警的关键是对车辆危险驾驶行为如危险换道、危险跟驰等进行高效和准确的识别与分析。基于此，本文以危险跟驰行为作为研究对象，通过对高速公路交通流特征参数的分析，提出了考虑行驶速度和车辆碰撞时间(time to collision, TTC)的危险跟驰行为分类标准及标定方法。通过使用前向–后向算法降低计算复杂度并利用Baum-Welch算法进行含隐状态的参数学习，构建了基于隐马尔可夫(HMM)模型的危险跟驰行为识别方法。结果分析和案例验证表明，本文所提出的HMM模型对于危险跟驰行为的识别精度较高，可以用于危险跟驰的碰撞预警，提升道路交通安全。

Abstract: With the development of automotive intelligence, collision warning has become an important re-search content in active safety technology. The key of collision warning is to recognize and analyze dangerous driving behaviors such as dangerous lane changing and dangerous car following efficiently and accurately. Based on this, the paper takes dangerous car following behavior as the research object, and puts forward the classification standard and calibration method of the behavior considering driving speed and time to Collision (TTC) by analyzing the characteristic parameters of the highway traffic flow. By using the forward-backward algorithm to reduce the computational complexity and the Baum-Welch algorithm to learn parameters with hidden states, a method based on Hidden Markov Model (HMM) is constructed to identify the dangerous car following behavior. The result analysis and case verification show that the HMM model proposed in this paper has high recognition accuracy for dangerous car following behavior, which can be used for collision warning of dangerous car following behavior to improve road traffic safety.

1. 引言

随着我国城市化水平的进一步提高和道路系统的不断完善，汽车已成为我国普通民众享受出行便利所必不可少的交通工具。汽车保有量增加所带来的交通问题也日益严重，威胁着人们的生命财产安全。根据历史数据统计，我国每年有超过10万人死于交通事故，而其中80%都是人为因素导致的 [1]，其外在表现就是“危险驾驶行为”。危险驾驶行为的出现会对道路交通安全造成不同程度的影响，因此，提前获取驾驶人的车辆运动状态信息，对潜在风险进行预警，可以减少事故的发生。

近年来，研究者们针对驾驶人行为的识别进行了广泛的研究。Oliver等人 [2] 通过驾驶人感知和车辆动力学数据建立隐马尔可夫模型，识别了换道、转弯等七种驾驶行为。同济大学的吕岸基于驾驶模拟器实验数据，验证了隐马尔可夫模型对高速公路中车辆超车行为辨识的有效性 [3]。Xing等人 [4] 利用驾驶图像数据进行驾驶员分心识别，开发了基于深度卷积神经网络(CNNs)的驾驶员行为识别系统。宋晓琳 [5] 等人将驾驶人总收益引入意图识别网络，提出了一种基于长短期记忆网络(Long Short Term Memory, LSTM)的换道意图识别方法。现有研究分析表明，学者们主要基于多元数据，利用机器学习算法实现车辆换道、超速等驾驶行为的识别。但针对危险跟驰行为的定义及研究较少，存在驾驶行为难以刻画和观测等问题。

针对上述问题，本文在前人研究的基础上，提出考虑危险划分方法的高斯混合隐马尔可夫模型，对车辆危险跟驰这类不可观测的驾驶状态进行识别，在一定程度上对危险跟驰行为进行提前预警，以提高驾驶安全性，有效避免交通事故的产生，提升道路通行能力。

2. 跟驰行为特征参数分析

根据国家统计局官网提供的数据，2019年，我国追尾事故占高速事故总量的45.7%，日常驾驶过程中有不少驾驶员存在着不良的跟驰驾驶习惯从而导致事故的发生。研究表明，结合速度、加速度这两个瞬时运动参数来描述车辆的驾驶动机，来分析驾驶人的危险驾驶行为是可行且有效的 [6]。因此，本节主要对美国联邦公路公路局所采集的NGSIM数据中的I-80高速场景的轨迹数据进行分析和统计学描述，作为模型输入参数的选择依据。

I-80数据的拍摄地点是美国加州80号洲际公路，数据为0.1 s/帧的车辆轨迹数据。该数据集的主要数据信息如表1所示，包括车辆纵向的速度、加速度，车辆的全局、局部坐标以及与前车的间距等。

Table 1. Characteristic information in NGSIM data set

表1. NGSIM数据集特征信息

2.1. 车辆速度特征分析

车辆速度是反应车辆运动状态的最基础和重要的参数，当驾驶员驾驶行为发生改变时，速度会发生最直接的变化。因此，对该数据集中的车辆速度参数进行统计分析。速度频率分布拟合图、累计百分频率图以及统计参数表如下所示。可以看出其分布符合期望为8.67，标准差为3.83的正态分布规律。结合图1和表2可以看出，该数据集的平均速度在8.65 m/s，车辆在该条道路上的行驶速度较慢。根据美国限速标准来看，该数据集中并没有车辆超速行驶。

Table 2. Statistics of speed parameter

表2. 速度参数统计表

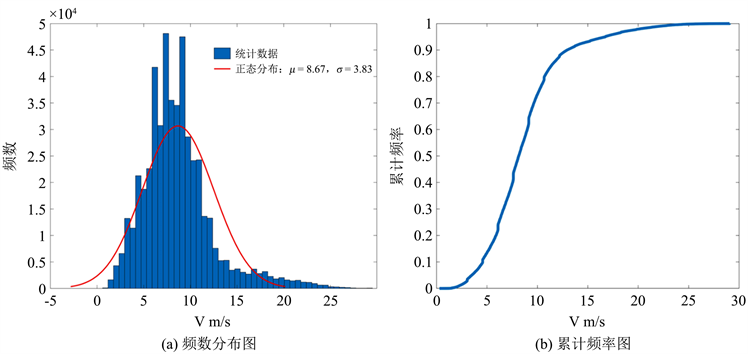
Figure 1. Analysis of Velocity characteristic

图1. 速度特征分析图

2.2. 车辆加速度特征分析

加速度表示速度的变化量，它能直接反映驾驶人对于周围环境的反应以及对车辆的控制。其频率分布拟合图如图2所示，符合期望为−0.08，标准差为1.15的正态分布。可以看出加速度在0值分布远远大于其他值的概率，这可能是由于车辆大都匀速行驶或者加速度传感器在数据趋于0时不准确而造成的。

Figure 2. Distribution of acceleration frequency

图2. 加速度频数分布图

2.3. 车头时距特征分析

车头时距是评价驾驶安全性的重要指标，与驾驶行为密切相关。其频率分布拟合图如图3所示，符合期望为0.85，标准差为0.39的对数型正态分布。可以看出，该数据集的车头时距分布主要集中于[1, 3]区间内。当车头时距大于10 s时，其频数趋近于0。

Figure 3. Distribution of time headway frequency

图3. 车头时距频数分布图

3. 危险跟驰行为的定义与划分

目前，国内外在车辆的防碰撞预警和危险划分指标的研究上有了一定的成果，工程中应用最广泛的为TTC指标 [7]，指两车保持当前时刻速度差至两车发生碰撞的时间，也就是驾驶员避免碰撞的最短反应、操作时间。研究者们通常采用1.5~10 s的固定TTC阈值来进行冲突风险的评价，Hirst等 [8] 将TTC处于0~3 s时定义为高风险，3~5 s定义为中风险，认为大于5 s时不存在碰撞风险。Wang Chang等 [9] 经过实车实验，将人的主观感知考虑到TTC中，根据换道车辆不同的相对时间及相对速度进行TTC阈值的划分。王颖等 [10] 基于TTC探究了车辆类型、载荷、超速三因素对于车辆碰撞风险的影响。但基于上述的固定TTC阈值在实际的车辆运行环境中可能会造成对低速行驶车辆的提前危险预判以及对高速行驶车辆的延迟危险预判。

以前后车相对距离为20 m，速度差为5 m/s，驾驶员反应时间为0.5 s为例：

1) 如图4所示，可以看出当相对距离和速度一定，TTC保持不变为4 s，以固定阈值进行划分时车辆始终为中风险跟驰状态。

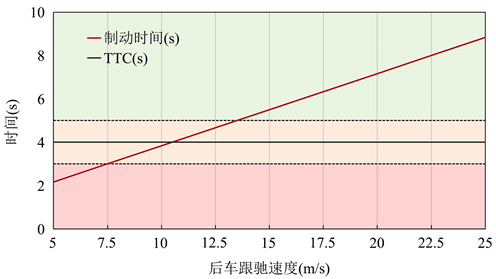
Figure 4. Classification of dangerous car following behavior by different methods

图4. 不同方法危险跟驰行为划分

2) 低速行驶车辆的提前危险预判：当车速低于7.5 m/s时，制动时间和固定TTC阈值都判断车辆处于危险跟驰状态，但TTC划分方法比制动时间提前1 s进行危险判定，提前危险预判预警在实际行驶中可能造成驾驶员对危险情况的不重视。

3) 高速行驶车辆的延迟危险预判：当车速位大于7.5 m/s时，制动时间判定车辆为危险跟驰状态，而固定阈值认为车辆处于中低风险跟驰状态，这会导致高速行驶车辆追尾事件的发生。

由于车辆跟驰状态存在差异性，为避免过早或过晚对危险跟驰行为进行识别预警，在以TTC进行危险定义时，需将后车跟驰速度考虑进来，使其状态划分呈线性增长趋势。因此，本文结合I-80数据集速度分布特征对危险跟驰行为状态进行标准定义，主要根据车速分为低速、中速和高速三种阈值等级的划分，如图5和表3所示。

Figure 5. Division of dangerous car following behavior

图5. 危险跟驰行为划分图

Table 3. Division of dangerous car following behavior

表3. 危险跟驰行为划分

基于驾驶员危险感知理论可知：当车辆可能与前车发生冲突时，若车辆驾驶人能适当地调整汽车行驶速度、方向或路线，及采取合适的避险行为，便可以化险为夷使碰撞得以避免。因此，避险行为的产生标志着交通冲突的产生，避险行为的采取又可以减轻和避免进一步的交通冲突。一般在发生冲突时，冲突当事者会采取制动、转向、加速、制动转向、加速转向等避险行为来减轻冲突严重程度。此外，结合第2章有关跟驰行为的特征参数分析，本文选择速度、加速度以及车间距作为特征因子输入模型，并以表3作为危险跟驰行为的判定标准进行数据标定。

4. 基于HMM的危险跟驰行为识别方法

4.1. 模型选择

4.1.1. 隐马尔可夫模型

隐马尔可夫模型(Hidden Markov Model, HMM)是一种在马尔可夫模型(Markov Model)基础上，由美国科学家Leonard E. Baum等人在二十世纪六十年代后半叶提出的可通过外部观测变量描述具有隐含状态的马尔可夫过程的数据统计模型，目前已成为经典的机器学习模型之一。HMM模型主要包含五个要素，分别是两个序列和三个模型参数；其中两个序列分别为隐藏序列 $Q=\left(q_1,q_2,\cdots ,q_T\right)$ 和观测序列 $O=\left(o_1,o_2,\cdots ,o_T\right)$。隐藏序列中的变量 $q_i$ 是指不可以被观测到的变量，也被叫做隐状态；观测序列O中的变量 $o_i$ 可以被直接观测到，因此也被叫做可观测变量。隐状态的取值集合可表示为 $S=\left(S_1,S_2,\cdots ,S_N\right)$，N表示可能的状态数；可观测变量分为离散和连续两种情况，对于离散的可观测变量来说，取值集合可表示为 $V=\left(V_1,V_2,\cdots ,V_M\right)$ ；其中M为可观测的变量数。

HMM的模型参数由λ表示，λ包含了初始概率分布π，状态转移概率矩阵A；观测概率矩阵B。隐马尔可夫模型λ用三元符号表示如下：

$\lambda =\left\{\text{π},A,B\right\}$ (1)

始概率分布表示为：

$\text{π}=\left\{{\text{π}}_1,{\text{π}}_2,\cdots ,{\text{π}}_N\right\},{\text{π}}_i=P\left(q_1=S_i\right)$ (2)

其中i表示初始时刻处于状态 $S_i$ 的概率。

状态转移概率矩阵A表示为：

$A={\left[a_{ij}\right]}_{N\times N}$ (3)

其中， $a_{ij}=P\left(q_{t+1}=S_j|q_t=S_i\right)$， $1\le i$， $j\le N$。 $a_{ij}$ 表示在t时刻处于状态 $S_i$ 的条件下，在t + 1时刻转移到状态 $S_j$ 的概率。

观测概率矩阵B表示为：

$B={\left[b_{jk}\right]}_{N\times M}$ (4)

其中， $b_{jk}=b_j\left(O_t\right)=P\left(O_t=V_k|q_t=S_i\right)$， $1\le k\le M$， $1\le i\le N$。 $b_{jk}$ 表示在t时刻处于状态 $S_i$ 的条件下产生观测序列 $V_k$ 的概率。

4.1.2. 高斯混合隐马尔可夫模型

根据隐马尔可夫模型中观测概率矩阵B分布的不同，可以将其分为连续型隐马尔可夫模型、半连续型隐马尔可夫模型和离散型隐马尔可模型。由于车辆行驶是一个连续的过程，因此我们使用的是连续的观测序列值，而高斯混合隐马尔可夫模型(Gaussian Mixed Model-Hidden Markov Model, GMM-HMM)在连续的观察序列中有着良好的表现，故本文选择使用GMM-HMM。该模型使用混合高斯函数来拟合连续性的观测值，混合高斯概率密度的形式为：

$b_j\left(O\right)={\displaystyle {\sum }_{m=1}^M{c}_{jm}N\left(O,{\mu }_{jm},U_{jm}\right),}1\le j\le N$ (5)

其中，O表示待拟合的观测序列； $c_{jm}$ 表示混合权重，即隐状态为 $S_i$ 时第m个混合系数，同时也满足 ${\displaystyle {\sum }_{m=1}^M{c}_{jm}}=1$， $c_{jm}\ge 0$ ；M为隐状态为 $S_i$ 时高斯分量的数目； $N\left(O,{\mu }_{jm},U_{jm}\right)$ 表示的是高斯概率密度函数； ${\mu }_{jm}$ 表示的是隐状态为 $S_i$ 时第m个混合成分的均值向量； $U_{jm}$ 表示的是隐状态为 $S_i$ 时第m个混合成分的协方差矩阵。GMM-HMM的模型参数可以表示为：

$\lambda =\left\{\text{π},A,c,\mu ,U\right\}$ (6)

此外，本文在利用隐马尔可夫模型进行危险跟驰行为识别建模时主要涉及两个问题：一是观测序列概率 $P\left(O|\lambda \right)$ 的计算，由于直接计算时间复杂度太高，因此在解决该问题时利用动态规划中的前向–后向算法，通过递归方式简化计算复杂度。二是HMM的参数学习，即极大似然估计求解问题，由于HMM包含隐状态，该问题无法通过直接求导法求解，所以本文采用Baum-Welch算法 [11] 进行求解。

4.2. 危险跟驰行为识别方法构建

为了对交通场景中最常见的跟驰行为进行分析，本文针对NGSIM数据集中位于同一车道前后相邻车辆的数据进行匹配，并根据其相对位置和速度数据计算两车的TTC，计算公式如下：

$\text{TTC}=\frac{y_f-y_r}{v_r-v_f}$ (7)

式中， $y_f$ 表示前车的纵坐标， $y_r$ 表示后车的纵坐标； $v_r$ 表示后车纵向车速， $v_f$ 表示前车纵向车速。通过第3章所定义的标准，首先使用考虑速度的TTC对每一时刻的跟驰行为属性进行设定。本文所采用的GMM-HMM模型以n个连续的时间步数据作为模型输入的一个观测序列，NGSIM数据集中的数据采样频率为0.1 s，故时间步的长度为0.1 s。其次对数据集进行标定，当前观测序列的隐状态标签由下一观测序列的属性决定，当下一观测序列所有时间步的属性均为中风险或高风险时，标定当前观测序列的标签为危险跟驰，否则标定为安全跟驰，如图6所示。

Figure 6. Calibration of dangerous car following behavior

图6. 危险跟驰行为标定

此外，为了能够显著区分车辆的跟驰行为，本文选择了前车速度、前车加速度、前后车距离、后车速度、后车加速度作为观测变量。表4是可观测变量为五的部分危险跟驰训练样本：

Table 4. Training cases of dangerous car following behavior

表4. 部分危险跟驰训练样本

通过上述方法分别得到危险跟驰和安全跟驰的训练集和测试集，两者数据量之比为3:1。为了识别驾驶人的跟驰行为，需分别训练安全跟驰单元模型 ${\lambda }_1$ 和危险跟驰模型 ${\lambda }_2$。GMM-HMM模型参数训练的步骤如下：

1) 确定初始参数。

本文中隐状态为安全跟驰行为和危险跟驰行为，所以N取值为2，观测变量O是一个5维变量，包括前车的速度、前车的加速度、前后车的距离、后车的速度、后车的加速度。此外，由于单高斯分布已经可以很好地描述大多数情况下的概率分布情况，因此本文将两个隐马尔可夫模型的M值均设为1，相应地，高斯分布权重系数C也设为1。一般情况下，π和A的初值选取对模型的影响不大，本文用随机数生成的方法，分别给两个模型的π和A设定初值。单高斯分布的均值μ和协方差矩阵U的初值通过抽取数据集中的部分样本估计得到。

2) 取训练集中的观测序列输入GMM-HMM模型，利用前向–后向算法，计算出前向概率和后向概率。

3) 通过Baum-Welch算法进行模型参数重估，更新模型参数λ。

4) 再次利用前向–后向算法，计算隐马尔可夫模型输出的似然概率，若概率增加，则需要重复步骤2)和3)，直到参数逐渐收敛不变，保存安全跟驰的模型参数λ₁、危险跟驰的模型参数λ₂。

训练完成后，将测试集中的观测序列输入到安全跟驰模型与危险跟驰模型中，得到两个似然概率，对其进行比较，较大者即为跟驰行为的识别结果，过程如图7所示。

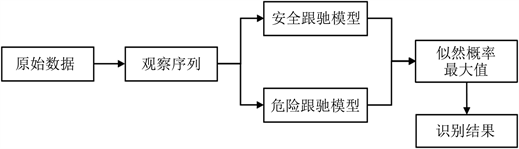
Figure 7. Identification process of dangerous car following behavior

图7. 危险跟驰行为识别流程图

5. 方法验证及分析

5.1. 观测序列长度影响分析

观测序列长度的选择对驾驶行为的状态识别有重要影响 [12]。长度过大会使单个序列内的数据包含多个行为特性，进而降低识别效率；长度过短会使单个序列内的数据特征不明显，不符合实际情况。因此，本文选取的观测序列长度范围为0.5 s至2.0 s。

图8所示的分别是危险跟驰行为和安全跟驰行为的识别准确率。从图中可以看出，安全跟驰行为的识别准确率没有随观测序列长度的增加而变化，且准确率都达到了90%以上。相对于安全跟驰行为，危险跟驰行为的识别准确率较差。此外，危险跟驰行为的识别准确率随观测序列长度的增加略有下降趋势，但在0.5 s至2.0 s的长度范围内，识别准确率也基本达到了80%以上。

Figure 8. Length calibration of observation series

图8. 观测序列长度标定

5.2. 结果分析

在对数据集进行统计学描述的基础上，本文采用危险感知理论定义了危险跟驰行为，确定了输入特征向量，最终采用0.5 s作为观测序列长度进行数据采集和处理。选择测试集中的311个样本数据，使用训练好的高斯混合隐马尔可夫模型进行计算，分别得到安全跟驰模型以及危险跟驰模型输出的两个似然概率值，并取其对数进行比较，确定识别结果。对模型性能进行检验，如表5所示，由于车辆观测数据波动较小、行为相对简单，模型对安全跟驰行为的识别准确率可达到93.69%，识别效果较好；对危险跟驰行为来说，模型的识别准确率可达到近85%，可以为接下来的碰撞危险预警奠定良好的算法基础。

Table 5. Recognition accuracy of GMM-HMM

表5. GMM-HMM模型识别准确率

6. 结论

针对交通跟驰场景中危险碰撞预警这一难题，本文基于美国高速NGSIM数据集，首先选取每一辆车的速度、加速度、车头时距等指标来描述交通流运动参数，分析了车辆运动的交通流特性及其分布特征。考虑TTC和加速度，对危险跟驰行为进行定义，提出了适应不同跟驰速度的危险跟驰行为划分标准。其次，根据跟驰样本的数据特点，使用前向–后向算法对HMM模型的状态转移概率进行求解，使用Baum-Welch算法进行高斯混合隐马尔可夫模型的参数训练，通过对310个危险跟驰行为以及618个安全跟驰行为样本进行训练，最终得到危险跟驰以及安全跟驰两个模型用于危险跟驰行为的识别。经311个测试集样本检验，结果表明样观测序列长度的设定会对危险跟驰行为的识别准确率产生影响，在步长为0.5 s时识别效果最好，辨识准确度约为85%，可应用于车辆跟驰过程中的碰撞危险预警。

基金项目

本文得到国家重点研发计划资助(编号: 2018YFC0807500)。

NOTES

^*通讯作者。