1. 引言
钢筋混凝土(RC)剪力墙因其强大的刚度和承载能力以及良好的延性，成为高层和超高层结构最重要的抗侧力构件。有关其抗震性能的研究一直深受国内外学者的关注。剪力墙的计算模型大致可以分为微观模型和宏观模型两种。微观模型采用实体等有限元模型 [1] [2] [3] 直接模拟剪力墙，理论完备但计算量大，不太适合用于整体结构的分析。在对混凝土微观力学行为还有诸多不确定性的现状下，基于合理的力学行为简化的基础上提出的宏观模型 [4] [5] [6]，更能体现结构的整体响应，同时计算量显著减小，适用于整体结构的抗震性能分析。
本文在多垂直杆单元模型的基础上提出考虑钢筋滑移的多垂直杆单元模型，并在OpenSees平台上实现两类单元模型的宏观有限元模型建模。通过与模型试验的对比分析，验证改进的模型的可行性和优越性。
2. 考虑钢筋滑移的多垂直杆模型理论
2.1. 考虑钢筋滑移的MVLEM
多垂直杆理论用多个沿墙体宽度方向竖向布置的弹簧模拟剪力墙的压弯刚度，用水平布置的弹簧模拟剪力墙的剪切刚度，进而模拟剪力墙整体的受力性能。采用已有的多垂直杆模型理论，基于分离式建模的理念，本文在OpenSees平台创建了MVLEM模型，依据配筋信息和几何尺寸，将剪力墙划分成多个条带，用竖向的零长度单元模拟剪力墙条带的拉压力学行为，用水平的零长度单元模拟剪力墙的剪切力学行为，模型示意图如图1(a)所示。在验证基础模型切实可行的基础上，提出了可考虑钢筋滑移的MVLEM，该模型在每个剪力墙条带底部增加一个能描述钢筋滑移的零长度单元，用来模拟剪力墙内部钢筋滑移现象，模型示意图如图1(b)所示。
2.2. 拉压零长度单元的恢复力模型
模拟拉压力学性能的零长度单元的恢复力模型由剪力墙条带内的混凝土和钢筋的本构模型确定，混凝土本构模型采用修正的Kent-Park模型，钢筋本构模型采用理想的弹塑性模型。恢复力模型关键参数确定方法见表1。恢复力模型示意图如图2所示。
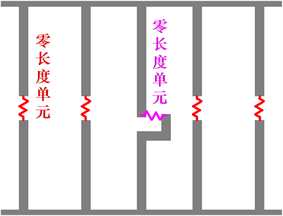
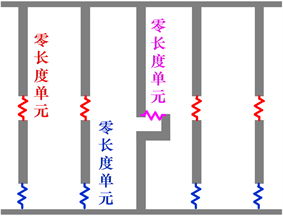(a) 不考虑钢筋滑移的多垂直杆单元模型(b) 考虑钢筋滑移的多垂直杆单元模型
Figure 1. Multi-vertical line element model
图1. 多垂直杆单元模型
Table 1. Key parameters of restoring force model of zero-length element for tension and compress
表1. 拉压零长度单元恢复力模型关键参数
Figure 2. Restoring force model of zero-length element for tension and compress
图2. 拉压零长度单元恢复力模型
2.3. 剪切零长度单元的恢复力模型
模拟剪切力学性能的零长度单元的恢复力模型采用考虑刚度退化的三折线模型，如图3所示。
恢复力模型的初始弹性剪切刚度
：
。
开裂后的剪切刚度与初始弹性剪切刚度的比值
：
。
屈服后的剪切刚度取为初始弹性剪切刚度的0.2%。
恢复力模型的开裂剪力
：
。
恢复力模型的屈服剪力
取为极限剪力
的0.85 [7]。
其中，G为弹性剪切模量，
为剪力墙截面面积，x为剪切变形的形状系数，h为墙体高度，
为墙体的有效水平配筋率，
为混凝土抗压强度。
Figure 3. Restoring force model of zero-length element for shear
图3. 剪切零长度单元恢复力模型
2.4. 钢筋滑移的恢复力模型
Sritharan和Zhao [8] [9] 认为钢筋滑移是由于一定锚固范围内钢筋应变渗透引起的，提出了考虑初始应变硬化率的钢筋滑移模型，其骨架曲线和滞回曲线示意图如图4所示。
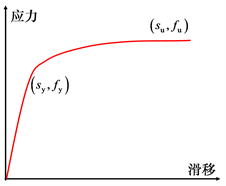
Figure 4. Restoring force model of bond-slip
图4. 钢筋滑移的恢复力模型
钢筋屈服时的滑移量
：
(1)
式中，d为钢筋直径，
为钢筋屈服强度，
为混凝土抗压强度，
为局部粘结滑移系数。
屈服后刚度取为初始刚度的30%~50%。
3. RC剪力墙试验数值模拟
采用多垂直杆单元模型和本文提出的考虑钢筋滑移的改进的多垂直杆单元模型，利用Matlab计算模型的关键参数，分别对现浇RC剪力墙模型试验和装配整体式RC剪力墙模型试验进行数值模拟分析。
3.1. 文献 [10] 现浇RC剪力墙试验
现浇RC剪力墙模型试验，选取文献 [10] 中的试件RW2作为分析对象，模型配筋信息如图5所示。模型示意图如图6所示。混凝土材料强度为27.4 MPa，钢筋屈服强度为414 MPa。不考虑钢筋滑移的数值模拟分析结果如图7所示，通过与试验结果的对比，验证了本文在OpenSees平台实现多垂直杆单元模型的可行性和正确性。考虑钢筋滑移的数值模拟结果如图8所示，通过与试验结果的对比，验证了本文提出的改进的多垂直杆单元模型相比多垂直杆单元模型，具有更高的精度。
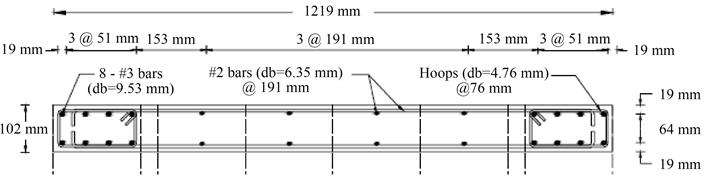
Figure 5. Section dimension and reinforcement of RW2
图5. RW2截面尺寸及配筋图
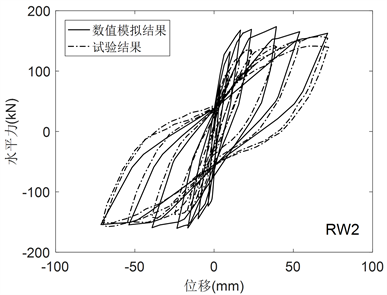
Figure 7. Numerical simulation without bond-slip of RW2
图7. RW2不考虑钢筋滑移的数值模拟
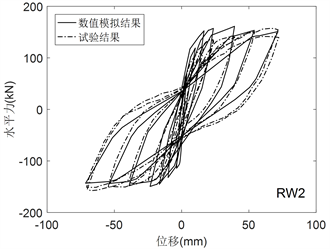
Figure 8. Numerical simulation with bond-slip of RW2
图8. RW2考虑钢筋滑移的数值模拟
3.2. 文献 [15] 装配整体式RC剪力墙试验
装配式整体RC剪力墙作为重要的抗侧力构件，在我国建筑工业化向着更高更广维度发展进程中，起着不可替代的作用，得到了广泛的应用 [11] [12] [13] [14]。本节针对采用国内自主研发的插入式预留孔灌浆钢筋连接的剪力墙模型试验 [15] 进行了数值模拟。试件尺寸及配筋信息如图9所示。根据钢筋直径的不同，搭接长度分别为380、440、505 mm，钢筋采用HRB335钢筋，混凝土选用C30。实测的材料性能见表2。试验采用循环往复加载，前期采用力控制，后期采用位移控制。不考虑钢筋滑移的数值模拟分析结果如图10所示，通过与试验结果的对比，验证了本文在OpenSees平台实现多垂直杆单元模型的可行性和正确性。考虑钢筋滑移的数值模拟结果如图11~13所示，通过与试验结果的对比，验证了本文提出的改进的多垂直杆单元模型相比多垂直杆单元模型，具有更高的精度。
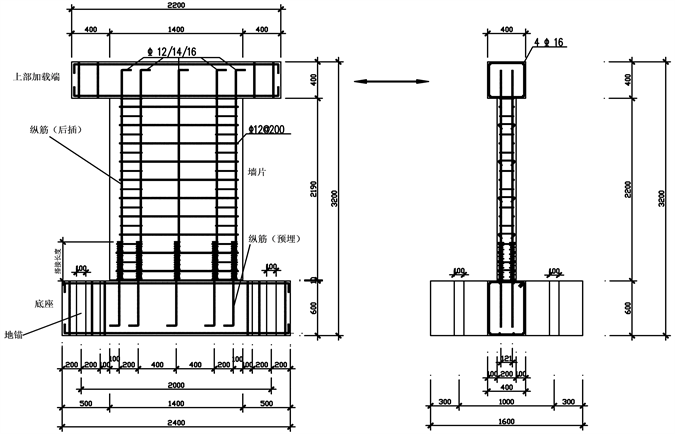
Figure 9. Dimension and reinforcement of specimens
图9. 试件尺寸及配筋信息
Table 2. Material parameters of specimens
表2. 试件材料参数
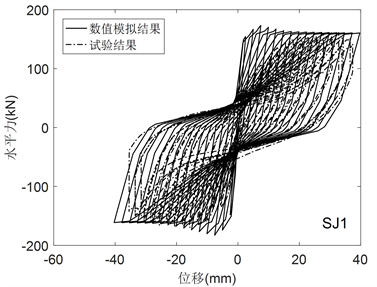
Figure 10. Numerical simulation without bond-slip of SJ1
图10. SJ1不考虑钢筋滑移的数值模拟
Figure 11. Numerical simulation with bond-slip of SJ1
图11. SJ1考虑钢筋滑移的数值模拟
3.3. 试验与数值模拟的对比
本文对数值模拟结果和试验结果的相对误差进行了定量评价。因为本文数值模拟分析采用的是位移加载模式，所以未单独对位移、延性等变形指标做定量对比，只对比了承载能力和耗能能力。试件加载过程中，试件的峰值承载力表征承载能力，滞回环累计包围的面积表征耗能能力，它能综合描述构件在地震中的耗能能力。相对误差定义：(数值模拟结果 − 试验结果)/试验结果，结果为正值表示高估了试件的能力，负值表示低估了试件的能力。对比结果见表3。从表中可以看出，考虑钢筋滑移的模型不同程度地提高了数值模拟结果的精度，尤其对于能综合表征力和变形指标的耗能能力。只有SJ3的分析结果不尽理想，主要原因是本文未对钢筋滑移模型做深入的研究。
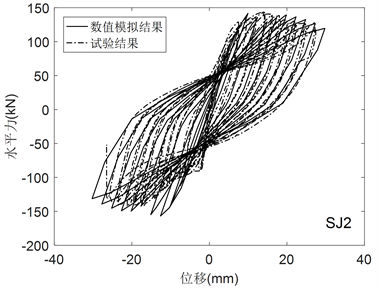
Figure 12. Numerical simulation with bond-slip of SJ2
图12. SJ2考虑钢筋滑移的数值模拟
Figure 13. Numerical simulation with bond-slip of SJ3
图13. SJ3考虑钢筋滑移的数值模拟
Table 3. Relative error between numerical simulation and test results
表3. 数值模拟结果与试验结果的相对误差
4. 结论
本文在多垂直杆单元模型的基础上，提出了考虑钢筋滑移的多垂直杆单元模型，并在OpenSees平台上实现了两类模型的有限元建模，通过与试验结果的对比，对模型的可行性和准确性进行了评定。主要得出如下结论：
(1) 在OpenSees平台中基于分离式建模的思想，建立多垂直杆单元模型和考虑钢筋滑移的多垂直杆单元模型是合理可行的。同时通过与已有试验结果的对比分析，验证了其模拟结果的准确性。该宏观剪力墙模型可用于高层、超高层等剪力墙结构体系的数值模拟，尤其对于装配整体式结构体系分离式建模具有重要的意义。
(2) 通过与试验结果的对比发现，钢筋滑移模型对数值模拟结果有重要影响，有关装配整体式剪力墙中的钢筋滑移模型等问题，还有待做更进一步的深入研究。