1. 前言
用频设备的互调干扰问题,一直是电磁兼容与防护的研究重点。目前的研究方法都是抑制互调产生的带外信号(谐波),无法解决互调产生的带内干扰信号。而实际上,互调产生的带内干扰才是最严重的问题。最根本的解决办法是在互调之前,就消除或抑制可以产生带内干扰信号的互调源信号,而这就需要全面厘清不同频率的互调源信号对用频设备的影响程度。基于前期提出的互调干扰预测建模方法,已经可以针对不同设备建立其自身二阶互调干扰的预测模型 [1] [2]。这就为接下来抑制互调源信号提供了基础。而抑制互调干扰最大的障碍之一就是插入损耗,这是不可避免的。必须寻求一种损耗低、抑制效果好且设计灵活简单,即可以根据干扰预测模型灵活变通地设计阻带的方法。基于此,前期提出了自适应陷波的数字滤波方法,取得了理想效果。但是该方法对采样频率要求很高,对于高频(微波以上)的用频设备,成本很高。因此尝试设计一种适合高频的微波双阻带滤波器。
图1给出了某型导航接收机的二阶互调阻塞干扰因子随辐射频偏变化的实测值,由此可见,互调干扰的敏感频带紧邻工作通带的两侧,且相对高频来说属于较窄的频带,且左右敏感频带不一定相同。这就为双阻带滤波器的设计提出了三点要求:1) 两个阻带中间是工作通带,因此中间通带的损耗必须极低,应该比带通滤波器要低;2) 倍频程衰减必须极大;3) 设计要简单灵活,且阻带通带要有比较高的可选择性,这样才能便于设计对应不同设备的滤波器。而双阻带滤波器的相关研究并不丰富,大多数并不同时满足以上三个要求。例如,利用开阶阻抗谐振器 [3]、有缺陷的阶梯阻抗谐振器 [4]、双层结构 [5]、基片集成波导 [6]、紧凑型嵌入残端 [7] 设计的双阻带滤波器虽然滤除性能很好,基于阶跃阻抗谐振器 [8]、双半波长谐振器 [9] 的设计也具有很高的选择性,但是位于中间的通带插损很大;而基于同轴集成 [10]、方形缺陷接地结构 [11]、双耦合频率捷变 [12]、多极点耦合线 [13]、阶梯阻抗发夹谐振器 [14]、耦合开放式希尔伯特谐振器 [15] 的设计具有良好的性能和选择性,但是倍频程衰减不够大;而基于基片集成同轴 [16] 和基片集成波导 [17] 的双频滤波器完美的满足了上述前两个要求,却不具有频带选择性和灵活性。
基于以上考虑,在前期建立的某型导航接收机的二阶互调干扰预测模型的基础上,采用直接耦合微波双阻带滤波器的合成和设计方法 [18] [19],并进行非对称改进 [20],设计出符合干扰预测模型的微波非对称双阻带滤波器,在左右敏感频带处设置两个阻带,使互调之前就能抑制或消除能产生带内干扰的互调源信号,以期望达到抑制二阶互调干扰的目的。
2. 互调干扰预测模型
根据之前总结的设备复杂电磁环境效应研究方法,已经可以得出某型导航接收机的二阶互调阻塞干扰模型,具体见文献 [1] [2],因内容较多,在此不再赘述,其带外敏感频带及阈值情况见图1和图2。图1横坐标为辐射频偏,表示干扰频率偏离中心工作频率的数值,负数表示低于工作频率,正数表示高于工作频率;纵坐标为二阶互调阻塞干扰因子,其数值即为阻带设计的指标。图2横坐标为辐射频差,即两个干扰信号的频率差值,纵坐标轴为二阶互调低频阻塞干扰电平相对值 [1] [2]。二阶互调阻塞干扰与两个干扰信号的频率差有关系,接收机只在图示的频率差范围内能够出现二阶互调敏感。图1和图2可以明确清晰地显示出二阶互调干扰对导航接收机的阻塞效应敏感条件,可以以此为基础设计相应的非对称双阻带滤波器,消弱二阶互调干扰对导航接收机的阻塞效应。
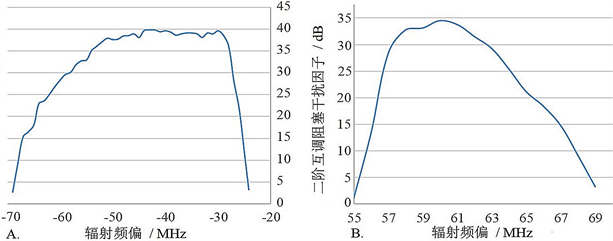
Figure 1. Second-order intermodulated blocking interference factor and radiation frequency deviation
图1. 二阶互调阻塞干扰因子随辐射频偏的变化
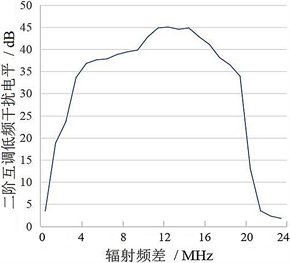
Figure 2. Second order intermodulated low frequency interference level and radiation frequency difference
图2. 二阶互调低频干扰电平与辐射频差
3. 非对称双带阻滤波器设计
由图1可见,某型导航接收机的二阶互调干扰敏感频带处于−70 MHz~−25 MHz和+55 MHz~−70 MHz频偏范围内,左右敏感频带与工作频点非对称,工作通带位于中间。这就需要非对称的双带阻滤波器 [4]。之所以不直接使用带通滤波器,是因为双带阻滤波器虽然对远离工作频率的频带没有效用,但是在通带内有更低的损耗和更高的处理功率 [3],在此不再赘述。该方法通过将波导、同轴、介质谐振器或平面技术综合实现,谐振器由耦合元件直接耦合,而不是由相位长度耦合。同时利用了两次频率变换而不需优化,即可完成从低通到双带通。然后根据带通与带阻的关系,将双带通的零点和极点变成双带阻的极点和零点,来设计两个指定阻带的滤波器,具有灵活简单的优点。下面简要介绍设计流程。
假设具体通带范围为
和
,图3所示的是两次频率变换的过程,ω表示低通滤波器所处的频域,f表示要设计的滤波器所处的频域。对单带通滤波器而言,通常是在ω域内设计,经过一次频率变换为f域。但是为了设计双带,需要对ω域中的频率响应连续应用两次频率变换才可以得到f域中的频率响应,因此引入
作为第一次变换后的中间频域 [20]。

Figure 3. Two frequency conversion processes
图3. 两次频率变换过程
从ω域到
域的频率变换如下:
(1)
(2)
其中,
,
。而
由
域的截止频率和给定的通带范围决定,
只能在
和
之间任意指定。表1为ω域到
域的频率转换关系。同样,
域到f域的转换关系如下:
(3)
其中,
。
也是由f域的截止频率和给定的通带范围决定,f0只能在fb1和fa2之间任意指定。三域之间的的截止频率转换关系见表1。

Table 1. Cutoff frequency conversion relationship of the three domains
表1. 三域之间的截止频率转换关系
由表1和公式(1)~(3)可得:
(4)
由上式可以基本确定双带通滤波器的基本参数,接着根据带通与带阻滤波器之间的关系,完成零极点的交换。从带通产生带阻特性,只需交换反射和传输函数(包括常量)即可 [20]:
(5)
最后,从
域滤波器的传输函数可以得到双阻带滤波器的耦合矩阵 [21],至此完成双带阻滤波器设计。
4. 仿真设计
根据图1的二阶互调敏感曲线,可得图4,即阻带设计的目标曲线。双阻带的设计应最大可能的拟合图4的曲线,并尽可能保证中间通带的损耗最小。按此要求,仿真设计一个10级的非对称双阻带滤波器。
首先,根据频带要求确定反射零点和传输零点,以确定滤波器的传递多项式。根据目标阻带要求和滤波器传输零点的选取规定,在ω域,传输零点在±1.4733处,而反射零点大概在±1.7213和±0.7402,具体方法可见文献 [19] [21]。结合公式(4)描述的频率变换关系,可以得到滤波器的主要参数见表2。
结合表2的参数,参照文献 [21] 的方法,计算出耦合矩阵,见下式:
(6)

Table 2. Specific parameters related to filter
表2. 滤波器相关具体参数
至此,完成该双阻带滤波器的设计。图5为该滤波器的频响函数与目标阻带曲线的对比。

Figure 5. Target stopband and filter frequency response curves
图5. 目标阻带和滤波频响曲线
由图5可见,仿真设计的滤波器阻带可以基本满足预设的目标要求。中间通带损耗为−0.42 dB。图6为该滤波器的拓扑结构图。
5. 结论
针对高频情况下的二阶互调干扰的问题,基于二阶互调干扰预测模型,利用直接耦合方式设计了微波双阻带滤波器。仿真证明该滤波器具有符合干扰预测模型的阻带,可以滤除40 dB以内的干扰,有效地抑制二阶互调干扰。