周期性换热蓄热式换热器的设计方法

Design Method of Periodic Regenerative Heat Exchanger

摘要: 目前，蓄热式换热器可以大幅提高设备的热交换效率以及温度效率，同时可以满足特殊换热环境下的需求。但对于换热温度、加热时间以及压降确定的情况下，传统方法无法完成蓄热式换热器的设计。本文以压降和加热时间为双重收敛标准，提出了一种新的周期性换热蓄热式换热器设计计算方法。克服了蓄热式换热器在周期性换热过程中不同流量和通流时间等约束条件下的设计难点，解决了其双向换热长度、加热时间、压降和温度分布等计算问题。本文提出的方法简化了蓄热式换热器的设计过程，具有很强的工程应用价值。

Abstract: At present, regenerative heat exchangers can greatly increase heat transfer efficiency and temperature efficiency, and can meet the requirements of special heat exchange conditions. But under the condition that heat transfer temperature, heating time and pressure drop have been determined, the traditional method cannot complete the design of regenerative heat exchanger. This paper proposed a new design method of periodic regenerative heat exchanger which takes the pressure drop and the heating time as the double convergence standards. This method overcomes the design difficulties of the regenerative heat exchanger in the periodic heat transfer process, such as different flow rates and flow time constraints. And the calculation problems of the bidirectional heat transfer length, heating time, pressure drop and temperature distribution are solved. The method proposed in this paper simplifies the design process of the regenerative heat exchanger and has a strong engineering application value.

1. 引言

随着热交换理论的不断完善以及钢材性能的提高，换热装置的换热性能得到了长足地进步。由于热交换器应用广泛，几乎涵盖所有的制造业等领域，根据其换热流体的物性、运行工况参数等特性，换热器结构和型式等都会产生相应的改变和调整。受换热介质的热物性影响，现行的换热器进一步提高热回收率受到了很大的限制。蓄热式换热器不仅能大幅提高设备的热效率，同时也能够得到较高的换热温度效率，使得换热后的流体可接近来流入口温度，广泛使用于高、中、低温热工设备。对于大规模储能系统，需要大量的蓄热介质。由于鹅卵石等价格低廉，填充床蓄热式换热器可以有效地降低投资成本，并且不会发生气化使得其在高温蓄热条件下更有优势 [1] [2]，在低温余热利用、工业废热利用以及太阳能蓄热等多个领域具有很好的适用性。近年来，国内外学者不断完善填充床理论分析和数学模型，并进行了大量的实验来辅助验证校核，已经获得了相对成熟的理论体系 [3] [4] [5]。同时针对流体质量流量、进口温度、周期性换热次数、换热效率等都进行了研究 [6] [7]。李朝祥 [8] 等针对蓄热式热交换器的设计提出依据混合扩散模型，在热交换器温度前沿扩展分析和换热效率的基础上，保证换热效率最高的约束条件下进行换热器的结构参数设计，对蓄热式换热理论进行了研究，但并未对周期性换热器的设计计算进行阐述。杜小泽等 [9] 设计了一种新型蓄热式管壳换热器，采用石蜡为相变材料，针对传热流体流速、相变材料导热系统及相变层厚度等关键因素，对换热单元的蓄/放热过程进行了数值模拟，对相变式蓄热器的设计进行了研究，理论与固体填充原理不尽相同。

传统的蓄热式换热器的设计方法，单向换热过程根据换热量、温度的时均值进行计算，换热时间、压降、换热流体换热器出口温度可以通过蓄热介质、蓄热器长度等进行计算 [10] [11]。但是当填充床蓄热式换热器应用于周期性换热环境时，其换热过程具有双向性，无法按照传统的单向换热进行设计计算。设计的蓄热式换热器需要满足较长时间的蓄热功能，同时还需要蓄热器出口温度要达到适合的运行工况温度。这对蓄热式换热器的设计计算提出了很高的要求，需要多方面综合考虑，包括换热器压降、不相等的换热时间、换热器出口温度要求等。田丽军 [12] 提出了一种组合填料式蓄热换热器，针对实验及模拟进行两方面研究，对其换热器传热动态过程及热工影响因素进行剖析，但并未对其蓄热换热器的设计进行阐述。杨万青 [13] 采用实验和理论相结合的方法研究了陶瓷球、陶瓷蜂窝体两类蓄热体的阻力及换热特性，并对回转型蓄热式换热器进行了热力计算与机械设计。其冷热流体研究对象换向时间较短，设计参数需要多次调整以便满足设计边界需求，关键参数仍可进一步调整优化。因此亟需提出一种新型的计算方法，快速收敛并简化计算过程，从而缩短设计周期。基于此，本文选取鹅卵石填充床蓄热式换热器为研究对象，分析了其关键参数对换热性能的影响，完成了填充床蓄热式换热器的计算流程设计。以压降和加热时间为双重收敛标准，设计了一种新的计算方法，克服了储释能过程中不同流量和通流时间等约束条件下的设计难点，解决了其双向换热长度、加热时间、压降和温度分布等计算问题，避免工程人员反复调整设计参数以满足设计约束，有效缩短周期性填充床蓄热式换热器的设计时间。

2. 蓄热式换热器的数学建模

蓄热式换热器工作原理：加热阶段是指高温流体在流经蓄热介质(鹅卵石等)组成的通道时，将热流体的热量传递给蓄热介质，等待加热过程结束后，切换流体流动方向，进入冷却阶段；冷却阶段是低温流体反向通入已加热的蓄热介质，流经通道时蓄热介质释放热量传递给低温流体，经加热后排出，冷却时间结束后完成整个换热过程。实际蓄热式换热器中的换热过程不可能出现上述平坦型温度前沿，由于高温流体和固体之间存在传热热阻以及固体内部导热热阻，热流体释放的热量不可能瞬间被蓄热介质所吸收，同时蓄热介质所吸收的热量也不可能瞬间在介质内部传导均匀，换热过程需要一定的时间，流体和固体之间也必然存在温差，由于混合扩散作用，使其偏离活塞流，换热过程不再是一个垂直的平面，形成了S型曲线的温度前沿，可以将这种温度前沿定义为“扩展型温度前沿”。其示意图如图1所示。

Figure 1. Extended temperature front

图1. 扩展型温度前沿

2.1. 填充床蓄热式换热器温度模型

填充床蓄热式换热器的工作状态随时间变化，其内部的热交换过程也随时间改变，故其属于非稳态热交换过程。本文采用混合扩散——中心对称模型(Dispersion Concentric Model)进行描述，在计算时作出以下假设 [11]：蓄热器内填充介质、工作流体温度分布均匀；换热过程不与环境发生热交换；填充介质之间的辐射传热可以忽略；流体与填充介质之间的对流换热系数、填充介质物性保持不变；

当热流体连续流入填充床蓄热器时，假设填充床的长度充分长，其内部流体各点温度随时间的连续分布可以表示为：

${\theta }_f\left(x,\tau \right)={\theta }_0\left(1-\frac{1}{\sqrt{2\pi {\mu }_2\left(x\right)}}{\displaystyle \underset{0}{\overset{\tau }{\int }}\exp \left(-\frac{{\left(\tau -{\mu }_1\left(x\right)\right)}^2}{2{\mu }_2\left(x\right)}\right)\text{d}\tau }\right)$ (1)

${\mu }_1\left(x\right)=\frac{x}{U}\left(1+\frac{a{c}_s{\rho }_{s}R}{3\epsilon c_g{\rho }_g}\right)$ (2)

${\mu }_2\left(x\right)=\frac{2x}{U}\frac{a{\left(c_s{\rho }_s\right)}^{2}R}{3\epsilon c_g{\rho }_g}\left(\frac{R^2}{15k_s}+\frac{R}{3h_p}\right)+\frac{2x{\alpha }_{ax}}{U^3}{\left(1+\frac{a{c}_s{\rho }_{s}R}{3\epsilon c_g{\rho }_g}\right)}^2$ (3)

其中： ${\alpha }_{ax}$ 为轴向热混合扩散系数；x为距蓄热器入口处的距离；U为气体的实际流速；R为填充床内固体颗粒的半径；c_g为气体的比热； ${\rho }_g$ 为气体的密度；a为固体颗粒的比表面积；k_s为固体颗粒的导热系数； $\epsilon$ 为床层的孔隙率； $\tau$ 为时间； $\theta =t-t_b$, $\theta =t_0-t_b$ ； ${\mu }_1$ 为密度分布曲线的中心位置 ${\mu }_2$ 为对应于中心位置的均方差；

当换热器充分长时，上式可较为精确的表示蓄热式换热器内沿长度方向各截面蓄热材料的平均温度随时间变化的连续分布。令换热器长度为L，当x = L时，

$\tau ={\mu }_{s1}\left(L\right)=\frac{L}{U}\frac{a{c}_s{\rho }_{s}R}{3\epsilon c_g{\rho }_g}=\frac{{\omega }_s{c}_s}{m_g{c}_g}$ (4)

${\sigma }^2=\frac{2L}{U}\frac{a{\left(c_s{\rho }_s\right)}^{2}R}{3\epsilon c_g{\rho }_g}\left(\frac{R^2}{15k_s}+\frac{R}{3h_p}\right)+\frac{2L{\alpha }_{ax}}{U^3}{\left(1+\frac{a{c}_s{\rho }_{s}R}{3\epsilon c_g{\rho }_g}\right)}^2$ (5)

式中： ${\sigma }^2$ 为温度分布的特征值； ${\omega }_s$ 为蓄热材料的质量；m_g为流体的质量流量；

经过化简整理，删除可忽略项可知

$\frac{1}{M^2}=\frac{{\sigma }^2}{{\tau }^2}=\frac{d_p}{L}+\frac{G_m{c}_g{d}_p}{3\left(1-\epsilon \right)h_{p}L}+\frac{G_m{c}_g{d}_p^2}{30\left(1-\epsilon \right)k_{s}L}$ (6)

式中：G_m气体的特征质量流率；d_p为填充床内固体颗粒的直径；M为 $\sigma$ 区间数。

其中M表示 $\sigma$ 区间数，对于 $\left(0,M\sigma \right)$ 域内，对于蓄热式换热器的温度分布进行积分，当M ³ 2.5时，可以认为其从0积分到1，即加热过程换热器高温介质入口处，高温流体与蓄热介质的温度近似相等，可以使得冷却过程出口温度有可能达到高温流体的入口温度，使得换热效率较高。故对于区间数M必须大于等于2.5，并且其值越大，代表蓄热器换热效果越好，将其作为一个重要的评价指标进行了详细地分析。

2.2. 填充床蓄热式换热器的压降模型

对于填充床压降的分析，国内外学者已经进行了大量的理论计算与实验研究，并将实验与理论相结合，拟合出多种假设条件下计算压降的公式。但这些公式仅仅适合特定的约束条件下才能使用。Ergun总结了不同学者的拟合公式，通过对流体流速、粘度以及密度和蓄热介质材料的孔隙率、粒径以及形状进行综合分析，推到出一个可以广泛应用的公式。故本章节采用的压降模型即经典的Ergun方程 [2]，公式如下：

$\frac{\Delta P}{L}g=150\frac{{\left(1-\epsilon \right)}^2}{{\epsilon }^3}\frac{{\mu }_g{U}_m}{d_p^2}+1.75\frac{1-\epsilon }{{\epsilon }^3}\frac{{\rho }_g{U}_m^2}{d_p}$ (7)

式中：DP为压力损失；g为重力常数； ${\mu }_g$ 为气体的粘度；U_m气体的特征流速。

3. 蓄热式换热器参数分析

针对填充床蓄热式换热器进行了参数分析，讨论了不同设置参数对填充床蓄热式换热器性能的影响，选择 $\sigma$ 区间数M为评价指标，其值越大，换热性能越好。针对流体特征流速U_m、蓄热器长度L、蓄热材料的平均直径d_p、密度 ${\rho }_s$ 、导热系数k_s以及比热容c_s对M的影响进行了全面地分析，计算结果如下。

由图2可知，蓄热体尺寸确定的情况下，当颗粒粒径为定值时，随着流体特征流速的增大， $\sigma$ 区间数呈现下降趋势，说明蓄热式换热器的换热效果变差。说明特征流速越低，换热效果越好。由图3可知，在其它参数一定的情况下，随着蓄热式换热器长度的增大， $\sigma$ 区间数呈现上升趋势，说明长度越长，换热效果越好。由图4可知，随着蓄热介质颗粒粒径的增大， $\sigma$ 区间数呈现下降趋势，说明颗粒粒径越小，换热效果越好。

Figure 2. Effects of the fluid characteristic velocity on M

图2. 曲线流体特征流速对M的影响

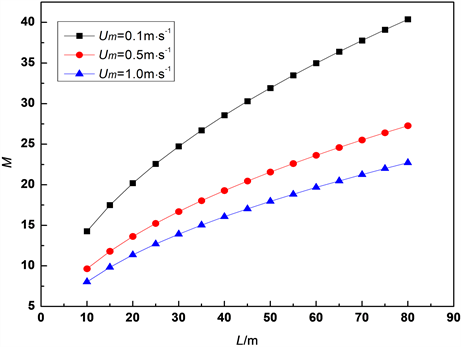
Figure 3. Effects of the length of regenerative heat exchanger on M

图3. 蓄热器长度对M的影响

Figure 4. Effects of heat storage medium particle size on M

图4. 蓄热介质粒径对M的影响

因此，在满足蓄热式换热器正常运行条件下，尽量选择较小的蓄热介质颗粒粒径；在满足流体压降的设置条件下，尽量选择较长的蓄热体长度以及较小的流体特征速度，可以获得较好的填充床蓄热式换热器的换热效率，能达到设计要求。

由图5所示，随着蓄热介质的颗粒密度的增大， $\sigma$ 区间数呈现上升趋势，说明颗粒密度越大，对填充床式蓄热器的换热性能有提升的作用。另一方面，随着颗粒密度的增加， $\sigma$ 区间数上升趋势逐渐变缓，并且其变化范围较小，对换热性能的影响较小。如图5所示，当颗粒粒径为3 mm时，其 $\sigma$ 区间数介于29.1~29.4之间。同时，当颗粒密度高于4000 kg×m⁻³时，区间数几乎没有发生变化，说明继续提高颗粒密度对蓄热器的换热性能也没有很明显的改善。

Figure 5. Effects of heat storage medium particle density on M

图5. 蓄热介质颗粒密度对M的影响

由图6所示，随着蓄热介质的颗粒比热容的增大， $\sigma$ 区间数呈现上升趋势，上升趋势越来越缓，并且比热容的改变对区间数改变量不是很明显，对蓄热器的换热性能改变也不是很大。由图7所示，随着导热系数的增大， $\sigma$ 区间数呈现上升趋势，在初期改变趋势较为明显，但当导热系数高于5 W×m⁻¹×K⁻¹时，区间数变化趋势逐渐变缓，换热性能提升也逐渐变缓。

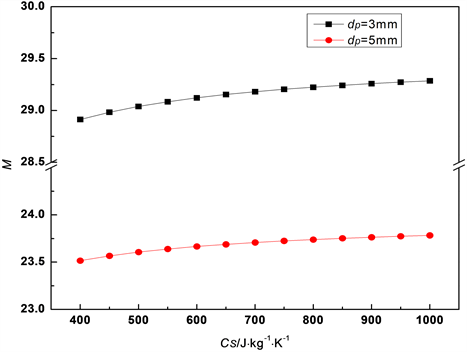
Figure 6. Effects of heat storage medium particle specific heat capacity on M

图6. 蓄热介质颗粒比热容对M的影响

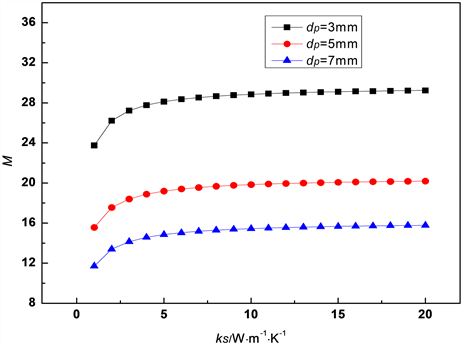
Figure 7. Effects of heat storage medium particle thermal conductivity on M

图7. 蓄热介质颗粒导热系数对M的影响

综上所述，蓄热介质的颗粒自身的密度、比热容以及导热系数属性对于换热性能的影响较小，因此在以后的研究讨论中，尽量选择较大的颗粒密度、比热容和导热系数，高于一定数值后换热性能敏感性会减弱。另外，应选取较小的颗粒粒径用以改善整个换热器的换热特性。同时，当满足流体压降的限制条件时，应尽量选择较长的蓄热体长度以及较小的流体特征速度。

4. 蓄热式换热器设计应用

4.1. 蓄热式换热器设计计算流程图

由于填充床蓄热式换热器的换热过程相对较为复杂，各种换热现象相互影响，如果采用传统的蓄热式换热器的设计方法，无法解决储释能过程中双向换热、流量和通流时间不同等约束条件下的设计难点，达到的效果如图8所示。针对这一问题，以压降和加热时间为双重收敛标准，设计了新的填充床蓄热式换热器计算方法，解决了其双向换热长度、加热时间、压降和温度分布等计算问题，详细计算流程如图9所示。

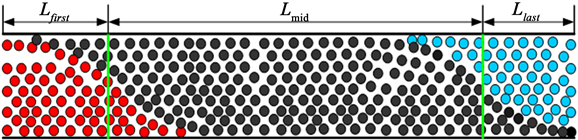
Figure 8. The actual effect that the heat exchanger needs to achieve

图8. 蓄热器实际需要达到的效果

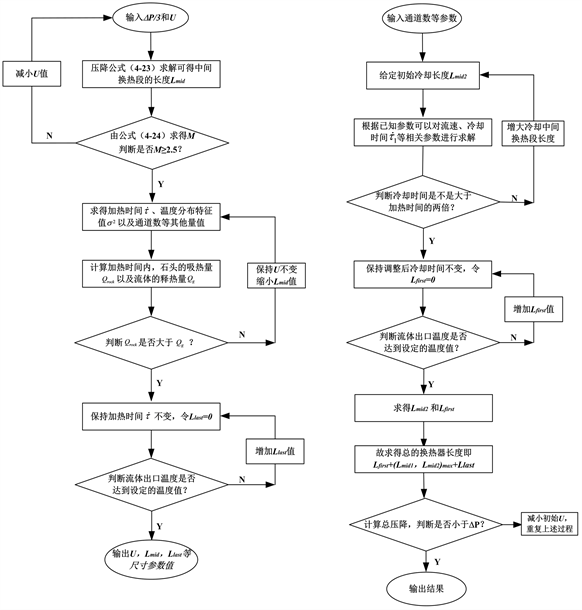
Figure 9. Design flow chart of packed bed regenerative heat exchanger

图9. 填充床蓄热式换热器的设计流程图

4.2. 蓄热式换热器设置参数

在计算过程中，蓄热材料的物性保持恒定，选取了空气的特定工况点为研究对象进行初步设计。具体参数设置如表1所示。

已知热流体进出口温度/压力以及冷流体进口温度/压力，假设冷热流体侧压降为1%，根据能量守恒，计算出冷流体出口温度/压力。根据质量守恒，设定加热时间和冷却时间分别为1 h、2 h。从而对蓄热式换热器进行设计计算。约束条件包括：冷热侧压降要小于1%；冷热流体进出口温度以及加热时间等与设计参数相一致。

Table 1. Basic setting parameters of regenerative heat exchanger

表1. 蓄热式换热器的基本设置参数

计算结果如表2所示，列出了三种填充床蓄热式换热器的基本结构参数。由于热流体侧的质量流量比冷流体侧大，在相同的蓄热体截面积下，其特征流速较快，从而导致其压降较大，因此只对热流体侧计算结果进行了罗列。

Table 2. Calculation results of regenerative heat exchanger

表2. 蓄热式换热器的计算结果

计算结果表明随着热流体特征流速的升高，蓄热体长度以及蓄热体直径都有所降低满足压降需求。经过计算，加热侧压降为工质压力的0.42%~0.44%，都低于1%，说明填充床式蓄热器设计压力达到收敛要求。另一方面，总的蓄热体体积及质量变化不大，长度和截面积变小使得通道数相应的增加。实际蓄热器设计可以根据场地大小，高度限制完成方案设计，为工程建造提供了数据支持，具有很好的工程应用价值。通过上述填充床蓄热式换热器的设计方法进行自迭代收敛，可以快速获得蓄热式换热器的结构参数，有效的缩短设计时间周期。

4.3. 结论

本文选取填充床蓄热式换热器为研究对象，分析了其关键参数对换热性能的影响，完成了填充床蓄热式换热器的计算流程设计，提出一种新的设计方法。

1) 依据蓄热介质的颗粒自身的密度、比热容以及导热系数属性对于换热性能的影响规律，较大的颗粒密度、比热容和导热系数性能较优，但高于一定数值后换热性能敏感性会减弱，因此选取合适的参数即可。另外，应选取较小的颗粒粒径用以改善整个换热器的换热特性。同时，当满足流体压降的限制条件时，应尽量选择较长的蓄热体长度以及较小的流体特征速度，以利于蓄热体的设计。

2) 以压降和加热时间为双重收敛标准，提出了一种新的填充床蓄热式换热器计算方法，无需多次人工调整关键设计参数，自收敛迭代计算，克服了蓄热式换热器在蓄能/释能过程中不同流量和通流时间等约束条件下的设计难点，解决了其双向换热长度、加热时间、压降和温度分布等计算问题，同时有效缩短了蓄热式换热器的设计时间，降低了工程设计人员人工调整工作量。

3) 该设计方法保证了换热器换热温度效率与热效率，使得其可以广泛应用于光热发电等高温换热工况以及液态压缩空气储能的低温工况中，解决了限制新能源推广的关键性技术问题，具有很强的工程应用价值。