1. 引言
手指静脉识别是模式识别和生物特征识别领域的研究热点。传统的身份鉴别方法具有易丢失、遗忘、安全性差等隐患,为了适应当前的信息安全需求以及使用便捷性,人们越发关注基于生物特征的身份鉴别技术的发展。人脸、虹膜、指纹都是生物特征识别的热点,但这些特征都存在一些应用上的不足,如人脸易受光照、化妆以及假脸的影响;虹膜采集要求高、设备便携性差;指纹易磨损,存在少部分人存在无指纹、指纹残缺的现象。相比于这些生物模式,手指静脉模式具有其得天独厚的优势。
手指静脉识别一般采用的是位于人体手指第二关节与第一关节之间的静脉血管网络影像图。由于,其无法通过表面成像,故目前都是采用近红外光对指静脉血管进行透射成像 [1]。因此,手指静脉除却高度便携的优点外,还具有抗伪性强、具有活体性、采集便捷友好等突出优点。这些优点促使这项技术飞速发展,并从实验室研究逐步走向实际场景应用。
医学研究发现,手指静脉血管网络结构的形成是结构性规律与随机过程的统一。因此,手指静脉的区分性来自于其自身的结构特征。但红外投射成像机制,由于光线在生物组织中,存在散射现象,导致采集图像中存在严重退化,这为完整的、可靠的提取血管网络结构带来了巨大困难。所以,传统方法大多是以图像处理方法为基础,采用纹理特征 [2] [3] [4] [5] [6] 的分析方法来解决手指静脉识别问题。
然而,传统特征提取和分析方法容易忽略血管网络的结构特性。图(graph)是一种数据结构描述方法,能够描述数据单元间的结构关系。基于图的特性,本研究提出将图与手指静脉识别进行结合,构建手指静脉图像的加权图模型,不仅能够描述图像全局的结构特征还能够通过边的权值来描述局部特征之间的关系。
图论的研究最早起源于1736年的哥尼斯堡七桥问题,之后逐渐发展成为了数学的一个分支,并广泛地运用于现代科学的许多领域,例如运筹学、数字图像处理、信息论、网络理论等领域 [7]。目前,图论在图像聚类、图像分割、模式识别方面都取得许多成果。2005年,罗斌、汤进 [8] [9] [10] 等人根据图谱理论提出基于内容的图像检索。2017年,Choi等人 [11] 提出一种基于无监督图学习的物体识别方法,在图像中设置随机游走的图模型,并通过学习图模型的变化来识别物体。近些年来,学者们尝试将图论与生物特征识别结合。相关研究可分为两类:1) 利用图模型来描述局部信息,将图论与编码相结合。这类研究包括基于局部图结构 [12] [13] 的人脸识别和人脸检测,基于多方向加权对称局部图结构的指静脉图像识别 [14],采用局部像素作为图的节点,构建局部的图模型。2) 利用图模型描述全局信息,将图论与图像纹理拓扑结构相结合。这方面的研究是近几年兴起的,相关的研究成果包括基于图模型匹配的指纹 [15]、视网膜 [16]、手部血管 [17] [18] 等,可将这类图模型称为生物特征图。由此可见,将图模型与指静脉识别相结合是有意义的。
在构建图模型时,节点的选择可为图像的像素点或者图像内容的细节点。由于图像尺寸较大,像素点数通常较多,这会使图的规模变得庞大,进而使得图的邻接矩阵维数激增,极大地增加了图匹配的负担;若选取图像细节点作为节点,手指静脉图像退化严重,图像内容细节点通常不稳定兼有因为图像增强带来的虚假细节点,这些因素会影响图模型的稳定性和图匹配的准确性。兼顾上述因素,本文利用图像的局部区域作为节点,对图像进行划分,将图块集抽象为节点集,提取图块的特征作为节点特征,通过三角剖分算法连接节点集,根据节点特征对图的边集进行赋值,从而获得手指静脉图像的加权图模型。
本文最后,针对上述构建的加权图模型,通过设置实验来分析,图模型中的相关参数对于识别效果的影响,并给出相应的结果分析。
2. 构图方法
令
为一个加权图,其中V,E,W分别代表节点集、边集和权重集。
,
,
,其中
。W中元素为非负实数,当满足
时,权值函数是对称的,图为无向图,反之则为有向图。
节点集V通过划分图像获得,
,n为图块数目,节点vi对应图像中第i个图块。图块划分时,假设图像尺寸为M × N,图块尺寸为h × h,以及k表示相邻两图块间交叠部分的尺寸,因此n可以通过式(1)计算得到。
(1)
其中,通过设置不同的k和h值,能够获得不同的图块划分结果,如图1所示。当k = 0时,图像分块等效为均匀划分,当k > 0时,等效为滑窗划分,注意k ≤ h/2。
图的边集E利用三角剖分算法连接相邻节点获得,记作
,其中eij为连接相邻节点vi和vj的边。通常认为图像的局部内容仅与相邻的图像内容相关性较高,其相关度随着距离的增加而下降,因此三角剖分算法能够很好的体现这种相关性,且这种节点连接方式的全局稳定性较好。在有向图中,当节点vi与vj满足
时
,如图2所示,其中r为图块列数即
。
权值函数W是用来描述节点间的特征表达。不同的权值函数能够为图附加上多种类型的图像细节信息,本研究中定义的权值函数如下:
(2)
(3)
(4)
(5)
其中,W(vi)代表节点vi所对应的图块特征,S(vi, vj)表征相邻节点vi、vj对应的图块特征的相似度。式(3)~(5)给出了三种W(vi)的计算方法,其中AAD代表绝对离散算子。
3. 特征提取
提取图块的定序编码作为节点特征。定序特征来源于对数量排序的测量,例如对比两个人年龄就是一种定序测量,因此其被广泛应用于社会类科学研究,也常用于非参数类的统计领域。
LBP是一种常见的图像编码方式,而LBP编码可以认为是中心像素与领域像素的定序测量结果。因此定序测量的概念被引入到人脸、虹膜、掌纹识别等应用场景,研究中发现其对光照和噪声鲁棒性高。在前述识别研究中 [19] [20],将定序测量与Gabor特征相结合,提出基于Gabor的定序编码(Gabor Ordinal Measure, GOM),该特征具备Gabor特征的独特性和定序测量的稳定性。
GOM提取过程中,首先利用Gabor滤波器对指静脉图像进行增强,然后将增强结果与多方向Gabor滤波器组进行卷积,获取图像的Gabor多方向幅度特征图,最后使用定序滤波器对Gabor多通道幅度特征图进行编码。定序滤波器中包含多个峰值和谷值,将定序滤波器与图像卷积,滤波结果为正,编码为“1”,反之为“0”,滤波结果为0是小概率事件。本文采用的定序滤波器如式(6)所示:
(6)
其中,
,
;
;其中θ是滤波器方向,(wx,wy),δ分别表示滤波器的中心位置和尺度,Np、Nn分别是滤波器正、负瓣个数,Cn、Cp是滤波器正负瓣调节系数,满足
;实验中采用三瓣定序滤波器,
,
,
,
,该滤波器效果较好,稳定性高。
图像中提取的特征呈矩阵形式,基于矩阵的图块间特征相似度计算公式如式(7)所示:
(7)
其中fi,fj分别为图块i,j的GOM特征,X,Y为特征矩阵的维度,σ为图块相似度的均值。图3为特征提取中各步骤结果。

Figure 3. The feature extraction results
图3. 特征提取结果
4. 图匹配
邻接矩阵用于记录图中各节点之间关系,记为AG,是一个n × n的矩阵,n为节点的数目,AG的行和列分别都表示图G的节点序列,若节点(vi, vj)之间有边连接,则矩阵中对应位置(i, j)处的元素值为边的权值wij,若节点(vi, vj)之间没有边连接,则对应位置(i, j)处为0,如式(8)所示:
(8)
本研究利用邻接矩阵来简化图匹配过程,通过计算两个矩阵的相似度来判断两个图的相似性,相似度计算如式(9)所示:
(9)
其中,p、q为矩阵的维数,
;
、
分别为矩阵A、B的均值。
通过观察可发现,三角剖分算法使得邻接矩阵具有高维稀疏的特点,其仅在特定位置有值,研究中可以利用这一规律进一步提高匹配效率。通过对矩阵中的非零数据进行提取和重新排列得到重构矩阵,重构矩阵可视作邻接矩阵的压缩结果。重构矩阵的每一列表述单一节点与其相连节点的权值关系,因此重构矩阵是一个m × n的低维矩阵,其中m为单一节点所连接的节点数,n为图模型的节点总数,如表1所示。

Table 1. Adjacency matrix reorganization
表1. 邻接矩阵的重构矩阵
5. 实验结果与分析
为了验证本文方法的鲁棒性,研究实验分别在两个图像库中进行。图库1为实验室自制的手指静脉图像库,其中包含5000张样本图像,共500类,每类10张图像,其采集图像和感兴趣区域(Region of Interest, ROI)图像如图4(a)所示;另一个来自于山东大学制作的手指静脉图像公开库,其中包含3816张样本图像,共636类,每类6张图像,其采集图像和ROI图像如图4(b)所示,从中提取100类组成图库2,共600张图像。实验中采用的测试集和训练集的比例为4:1,判别时选取平均相似度最大的类别作为图像的类别标签。

 (a) 图库1 (b) 图库2
(a) 图库1 (b) 图库2
Figure 4. Image of finger vein and its ROI image of different database
图4. 不同图库的原始指静脉图像以及其ROI图像
5.1. 不同权值函数对识别结果的影响
从第2节的图模型构建过程可以看出,选择合适的权值函数对图模型构建具有重要意义,进一步观察式(2)可以发现,图模型的权值函数的变化来自于W(vi)的选择,因此需要对式(3)~(5)所式的三个W(vi)函数进行进一步的讨论。在图库1和2中对比不同的W(vi)对识别结果的影响。
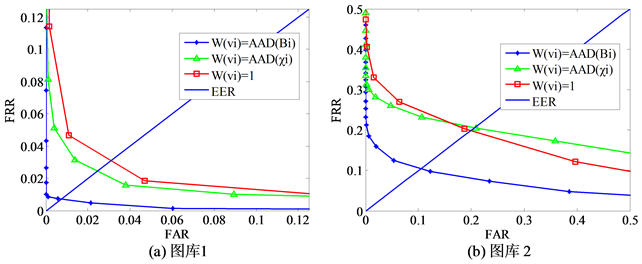
Figure 5. ROC curves of different weighting functions
图5. 不同权值函数的识别结果
从图5可以看出,当W(vi)如式(5)时,其识别结果最佳;当W(vi)如式(3)时取得的效果相对最差。因为当W(vi) = 1时,边的权值仅考虑节点特征之间的相似度而未考虑节点本身的特征,因此当计算边的权值时,加入节点本身的特征,有利于识别效果的提升。
5.2. 图块参数对识别结果的影响
图块参数包括图块的划分方式和图块的尺寸,图块划分方式和尺寸在一定程度上会影响GOM特征的效果,因此通过实验观察寻找最优的图块参数。其中当k = 0时,称为均匀划分,k > 0时,称为滑窗划分,本文实验中仅讨论k = 0和k = h/3两种情况。在图库1中进行图块参数的对比实验。

Figure 6. ROC curves of different block divisions
图6. 不同图块划分参数的识别结果
从图6可以看出,采用滑窗划分取得最佳效果时,图块尺寸要大于均匀划分的最佳效果,滑窗划分能够增加节点间的信息冗余,在一定程度上改善图像位移的影响,因此选用滑窗划分效果更好。
5.3. 识别结果对比
为了验证本研究所提出的方法的普适性,根据前两节实验所获得的构图参数,分别在两个图库中进行对比实验。实验中从图块划分方式出发对比识别性能,其中两种图块划分方式,采用相同的权值函数
,图块尺寸则根据第5.2节的结果,分别选取合适的划分尺寸,以获得最佳的识别效果,实验结果如表2所示。

Table 2. Recognition results of different databases
表2. 不同数据库识别结果
从表2中可以看出,本文提出的方法在两个图库中都能取得了较高的识别精度和识别效率,这说明本文方法在不同数据库中都具有鲁棒性,能够适应较多的应用场景。通过进一步对比观察可知,本文方法在图库2中的表现略逊于图库1,究其原因包括:图库2图片采集条件复杂,样本量少,样本存在漏光现象,类内存在较明显的翻滚姿态变化,使得类内特征图像差异大。这说明本研究还需要进一步研究姿态差异下的特征表达。
6. 结论
本研究提出了一种基于图模型与定序编码的手指静脉识别方法,首先对图模型的构建以及特征提取方法进行了阐述,说明了图结构能够兼顾全局结构特征以及局部图像特征的描述,并通过实验分析了图块划分方式、图块尺寸以及权值函数对识别结果的影响,证明了加权图模型在指静脉网络识别任务上的有效性以及普适性。
但本文还存在一定的问题:1) 图块划分是人为设定的,对于血管网络结构的描述仍有欠缺;2) 本文方法对于手指姿态变化较为敏感。这些问题都需要进一步研究。
NOTES
*通讯作者。