1. 引言
当温度升高,热扰动使得整个磁有序体系中的任意一个自旋发生翻转,相邻自旋在交换相互作用驱使下受到扰动而发生振荡并且偏离平衡点。这样的偏离平衡点的状态并不会仅仅局限于一个孤立格点,而是会不断向外扩散,最终弥散到整个系统。这种自旋振荡在系统中的扩散被称为自旋波。
与声波、晶格波等形式的波一样,自旋波是固体中一种重要的元激发。对自旋波进行二次量子化处理后,可以将其视为磁子(magnon)这种准粒子的集合 [1]。
后来,西韦和谈纳瓦尔德在坡莫合金(Ni80Fe20)薄膜中,观测到自旋波的共振现象,首次在实验上证明了自旋波的存在。20世纪90年代,微磁学模拟的蓬勃发展,为自旋波的研究开辟了新道路。微磁模拟研究清晰生动地展示了自旋波在铁磁薄膜中的动力学行为。随着研究的不断深入,人们逐渐意识到了自旋波的独特性质以及它广泛的应用前景。自旋波具有波的普遍性质,如反射、折射和透射等。在与磁拓扑孤子(磁涡旋态、磁畴壁、斯格明子等)相互作用时,自旋波会产生特殊的现象。通过设计、加工具有周期性纳米结构的磁性体系,研究人员提出了磁子晶体这一新研究领域。由于自旋波所处频段较高(一般在GHz范围),并且在传播过程中产生焦耳热少。因此作为新型的信息传播载体有着很大的应用潜力 [2] [3]。
根据德布罗意物质波理论,自然界中的波都具有动量
,其中
是普朗克常数,而
为波矢。20世纪,随着对光学领域研究的不断深入,人们发现光波除了具有动量p,通过特殊手段进行调控后,还能够携带轨道角动量L,其中
。这种带有轨道角动量的光波称为涡旋光。在铁磁材料中传播的自旋波,也能通过物理手段调控从而携带轨道角动量,这种携带轨道角动量的自旋波称为涡旋自旋波 [4]。
在传播过程中,涡旋自旋波会相对于相位奇点呈现螺旋状相位分布。其相位分布可以表示为:
。其中l是涡旋自旋波的拓扑荷数,
是相对奇点的相位大小。拓扑荷l代表着涡旋自旋波的不同性质,l可以取正也可以取负,当拓扑荷数m大于零时,代表此时涡旋自旋波的角动量旋性为顺时针;当拓扑荷数l小于零时,代表此时涡旋自旋波的角动量旋性为逆时针。同时,拓扑荷数l的大小代表相互交织的相位面的数目 [5] [6] [7]。
2019年,Jia等人首次提出在一个沿着垂直方向均匀磁化的纳米圆柱形长条中,在其底端施加拉盖尔–高斯函数形式的磁场,可以激发出具有轨道角动量的涡旋自旋波 [8]。随后,Jia等人又提出,除了利用外加带有空间各向异性的磁场来产生涡旋自旋波外,让平面自旋波通过一个螺旋状的相位波片也能让自旋波具有轨道角动量。于是,将平面波形式的自旋波穿过不同材质的螺旋相位面,他们又一次产生了具有轨道角动量的涡旋自旋波 [9]。在本文中,我们利用傅里叶分析,给出了纳米圆柱内涡旋自旋波的本征频谱,并且利用施加面内旋转磁场的方式激发出了涡旋自旋波。
2. 样品模型
在本文中,样品采用纳米圆柱进行微磁学模拟计算,其中纳米圆柱的直径d为200 nm,高度h为200 nm,其结构如图1所示。
模型采用软磁材料坡莫合金的参数,其中坡莫合金不存在磁晶各向异性,因此磁晶各项异性常数设置为:
;饱和磁化强度为
;交换相互作用系数
,阻尼系数
。在进行微磁学模拟计算时,将纳米圆柱划分为一系列大小都为
的网格。本文中微磁模拟所用的是一款基于有限差分法,由Mike Donahue和Don Porter开发的开源微磁模拟软件,OOMMF (Object Oriented Micromagnetic Framework) [10]。
纳米圆柱磁矩的初始分布设置为极性为
,旋性为
的磁涡旋态。为了获得一个较稳定的初始态并且降低运算时间,分为两步进行弛豫。首先,在设置好参数后,取一个较大阻尼系数
进行弛豫,得到第一个状态。从该状态开始,将阻尼系数改为
进行第二次弛豫。第一次弛豫的收敛条件设置为所有的磁矩每纳秒的进动不大于0.01˚,即收敛条件为
。而第二次弛豫的收敛条件设置为
。通过这种方法,可以较快地得到一个具有稳定磁涡旋态的纳米圆柱。同时,为了防止自旋波在纳米圆柱的顶端发生反射,干扰数据的分析,我们在纳米圆柱高度
的末端设置一个吸收区域,将其阻尼系数设置为一个较大的值
。

Figure 1. The initial magnetization distribution of the magnetic vortex state in a permalloy nanocylinder with a diameter and height of 200 nm, the polarity is upward, and the spin is counterclockwise, as shown by the arrow
图1. 直径和高度都为200纳米的坡莫合金纳米圆柱中磁涡旋态的初始磁化分布,极性向上,旋性为逆时针,如箭头所示
3. 涡旋自旋波的本征频谱及其模态
在这一节中,为了验证是否存在带有角动量的涡旋自旋波,需要对其振动的自旋波频谱和模态图进行分析。由于涡核极性会影响涡旋自旋波的拓扑荷数的正负,在这里我们分别对相同的样品参数设置极性分别为
,旋性都为
的磁涡旋态为初始态,然后再对两种不同的初始态加相同的脉冲场磁场,分别分析其本征频谱。我们首先对样品的第一层,即高度
的区域施加一个面内的sinc函数型脉冲磁场。我们的纳米圆柱样品在垂直方向(即z方向)一共被划分成40层,如果对每一层进行傅里叶分析需要大量的计算量,考虑到我们主要是为了验证自旋波在纳米圆柱内的传播是否具有角动量,因此需要尽量降低退磁场的影响。所以在进行频谱以及模态判断的时候,我们取退磁场最均匀的中间层的磁矩数据,对其面内的磁矩振动分量
进行傅里叶分析。在样品第一层,施加的x方向sinc脉冲磁场的表达式为;
(1)
其中
为sinc脉冲场的振幅,我们设置为1 mT,
设置为1 ns,f为截止频率,我们将其设置为20 GHz。经过傅里叶分析后,我们得到涡旋自旋波的频谱图,如图2所示。其中紫色实线代表涡核极性
时的
的涡旋自旋波频谱,黑色圆点代表涡核极性
时的
的涡旋自旋波频谱。我们发现两者的本征频谱一致,具有不同极性的拓扑荷数的涡旋自旋波本征频率相同。其中频率为0.35 GHz的峰对应的是磁涡旋态的旋进模式,而1.6、3.5、4.8、5.9、7.3、8.1 GHz对应阶数为
的涡旋自旋波模态。
为了进一步验证涡旋自旋波的存在,我们对特定频率下的磁矩振动模态进行逆傅里叶变换(inverse FFT,IFFT)。我们取自旋波频谱上本征频率为3.5 GHz的点,在自旋波的传播方向,即z轴方向上取纳米圆柱中层数为1,10,20,30,40层中的磁矩的振动模态进行逆傅里叶变换。得到沿z轴传播的自旋波的模态图,如图3所示。
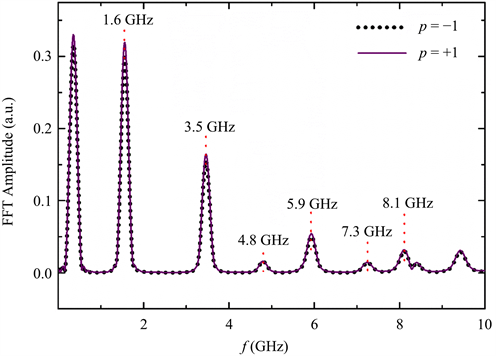
Figure 2. The spectrum diagram of the vortex spin wave, where the purple solid line represents the vortex spin wave spectrum of l = −1 when the vortex core polarity p = +1, and the black dots represent the spectrum of the vortex spin wave with l = +1 when the vortex core polarity p = −1
图2. 涡旋自旋波的频谱图,其中紫色实线代表涡核极性p = +1时的l = −1的涡旋自旋波频谱,黑色圆点代表涡核极性p = −1时的l = +1的涡旋自旋波频谱
从图3(a)中,我们可以看出,激发出的自旋波是沿着 轴传播的,并且通过对比沿着z轴不同层的模态图,我们发现,每层激发出来的都是阶数为1的角向自旋波,而且不同层之间的相位并不相同,每层之间的自旋波都存在一个相位差
。因此,通过对其模态图的分析,我们可以知道,利用上述方式所激发出的自旋波不仅具有动量,是沿着z轴直线传播的波,同时它还具有角动量
,使得处于z轴不同位置的波面的相位不同,发生了扭转,扭转方向为顺时针。我们将这种自旋波称为具有拓扑荷数
的涡旋自旋波,其角动量的大小可以定义为
,这里的f是涡旋自旋波的本征频率,在这里我们取3.5 GHz进行分析。
除此之外,我们发现,在保持旋性不变,将纳米圆柱中的磁涡旋态的极性改变为
时,也得到本征频率为3.5 GHz的涡旋自旋波模态。然而,在对其进行逆傅里叶分析后,我们发现涡旋自旋波的等相位面呈逆时针方向旋转,即它为
的涡旋自旋波,如图3(b)所示。通过对比,拓扑荷数不同的涡旋自旋波,处于本征模式下时,除了自旋波的相位面的扭转方向不同外,其余的性质,如本征频率,波长和波速等都一致。

Figure 3. Inverse Fourier analysis (IFFT) modal diagram of a vortex spin wave with an intrinsic frequency of 3.5 GHz at different positions on the z-axis. (a) The vortex spin wave mode diagram with topological charge l = −1; (b) The vortex spin wave mode diagram with topological charge l = +1
图3. 本征频率为3.5 GHz的涡旋自旋波,在 轴不同位置的逆傅里叶分析(IFFT)模态图。(a) 拓扑荷数为l = −1的涡旋自旋波模态图;(b) 拓扑荷数为l = +1的涡旋自旋波模态图
4. 拓扑荷数l = ±1的涡旋自旋波
在利用傅里叶分析得到sinc函数型脉冲磁场激发的涡旋自旋波的本征频谱,并利用逆傅里叶分析得到不同本征频率下的自旋波的模态图后。对纳米圆柱施加一个面内的旋转磁场可以激发出对应本征频率下的不同拓扑荷数
的涡旋自旋波。对于初始态为磁涡旋态的纳米圆柱,设置其涡核极性为
,旋性为
,在纳米圆柱高度
的区域施加一个逆时针的面内旋转场,其中旋转场的振幅为5 mT,频率为3.5 GHz,可以激发出拓扑荷数 的涡旋自旋波;另外,如果设置初始的磁涡旋态涡核极性为
,旋性还是
,对纳米圆柱在相同的区域施加频率和振幅相同的顺时针旋转场,可以激发出拓扑荷数
的涡旋自旋波。在时间
时,沿着z轴方向,不同位置的
的分布如图4(a),图4(b)所示。而拓扑荷数为
和
的涡旋自旋波的波阵面如图4(c)、图4(d)所示。
注意,不同的磁涡旋态的初始态,会对涡旋自旋波的拓扑荷数产生影响。为了探究涡核极性和旋性对涡旋自旋波角动量方向(即拓扑荷数的正负)的影响,我们设计了4种磁涡旋态的初始磁矩分布,分别为:1) 涡核极性朝上
,旋性为逆时针方向
;2) 涡核极性朝上
,旋性为顺时针方向
;3) 涡核极性朝下
,旋性为逆时针方向
;4) 涡核极性朝下
,旋性为顺时针方向
。对处于这些不同初始态的纳米圆柱分别施加振幅50 mT,各个本征频率下的逆时针(CCW)和顺时针旋转场。
通过对比结果,我们发现:涡旋自旋波的角动量方向与磁涡旋态的旋性无关,而是与涡核的极性相关。当涡核极性朝上
时,对纳米圆柱施加一个逆时针(CCW)的旋转磁场,可以激发出拓扑荷数为
的涡旋自旋波;当涡核极性朝下
时,可以激发出拓扑荷数
的涡旋自旋波。
这一现象可以由角向自旋波和涡核之间存在着的相互耦合作用来解释 [11] [12],当我们在纳米圆柱底层施加不同旋进方向的磁场时,可以激发出对应角向自旋波:施加逆时针的旋进磁场,可以激发出逆时针旋转的角向自旋波;施加顺时针的旋进磁场,可以激发出顺时针旋转的角向自旋波;同时,旋进磁场也会对涡核产生作用,使其发生微小的进动,涡核的进动会产生一个回旋场,这一回旋磁场会跟角向自旋波耦合。根据Curcic等人的研究,回旋场和角向自旋波的耦合与涡核极性相关:当涡核极性朝上时
,回旋场与顺时针旋转的角向自旋波耦合更强,这使得顺时针的角向自旋波无法在纳米圆柱的底部保持一个稳定的旋绕状态,因此无法稳定地朝着Z轴传播;相反,此时逆时针旋转的角向自旋波由于与极性朝上的涡核之间的耦合较弱,因此能够稳定地在圆柱内传播。这样,当涡核极性朝上,才能激发出拓扑荷数
的涡旋自旋波。同样道理,当涡核的极性朝下
时,回旋场与顺时针旋转的角向自旋波耦合较弱,与逆时针旋转的角向自旋波耦合较强,所以能在圆柱底部形成较稳定的顺时针旋转的角向自旋波。因此,拓扑荷数
的涡旋自旋波能在样品内稳定传播。
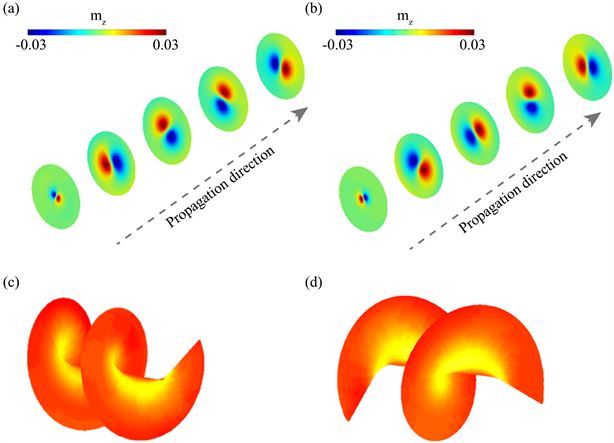
Figure 4. (a) When the propagation time t = 0.3 ns, the topological charge number l = −1 is the magnetic moment mz amplitude diagram at different positions of the nanocylinder along the propagation direction; (b) When the propagation time t = 0.3 ns, the magnetic moment mz amplitude diagram of the spin wave with topological charge l = +1 at different positions along the propagation direction of the nanocylinder; (c) (d) l = −1 and l = +1 vortex spin wave Schematic diagram of the wave front
图4. 本征频率为3.5 GHz的涡旋自旋波,在 轴不同位置的逆傅里叶分析(IFFT)模态图。(a) 拓扑荷数为l = −1的涡旋自旋波模态图,(b) 拓扑荷数为l = +1的涡旋自旋波模态图,(c) (d) 拓扑荷数为l = −1和l = +1涡旋自旋波波阵面
5. 总结
本文提出了一种全新的激发具备轨道角动量的涡旋自旋波的方法。在坡莫合金铁磁纳米圆柱底部施加x方向的sinc脉冲磁场,我们成功得到了铁磁纳米圆柱内涡旋自旋波的本征频谱,并且给出了3.5 GHz下的模态,通过施加3.5 GHz空间分布均匀的面内旋转磁场,可以激发出阶数为1的涡旋自旋波。
此外,我们发现在涡核极性朝上时,对磁涡旋态施加逆时针旋转的均匀旋转场(CCW),可以得到拓扑荷数
的涡旋自旋波;在涡核极性朝下时,对其施加顺时针的均匀旋转磁场(CW),可以得到
的涡旋自旋波。这是由于涡核在磁场的驱动下也会发生进动,这一进动会导致涡核附近产生一个回旋场,回旋场与涡核外部的角向自旋波发生耦合并会破坏角向自旋波的稳定性,最终导致其无法在厚度方向稳定传播,使得无法在圆柱中产生稳定的涡旋自旋波。当涡核极性
时,涡核进动产生的回旋场与顺时针角向自旋波的耦合强度要大于与逆时针角向自旋波的耦合强度,因此逆时针的角向自旋波更稳定,能形成对应的涡旋波。当涡核的极性
时,回旋场与逆时针角向自旋波的耦合强度要大于与顺时针角向自旋波的耦合强度,因此更易稳定地产生逆时针的角向自旋波以及对应的涡旋波。
未来我们将探讨平面自旋波通过一个特殊的具有一定旋性的结构,转变成涡旋波的可能性。并且探究二维的平面自旋波是否也能具备轨道角动量。并且设计具体的器件探究涡旋波的具体应用。
基金项目
本文作者感谢国家自然科学基金项目10974163和11174238支持。