基于分形理论的皖北矿区断裂复杂程度分析

Analysis of Fracture Complexity in Northern Anhui Mining Area Based on Fractal Theory

摘要: 根据分形理论，通过皖北矿区断裂网络的相似维数对其断裂复杂程度加以解释和分析。结果显示皖北矿区构造复杂区域较为集中，分维值较高。区域内的断裂构造具有较为明显的区域性，大小断层裂隙集中发育的密集区域其整体分维值下限大于1，构造复杂。其相似维评价结果与实际揭露基本吻合，评价结果较好。在评价中合理应用断裂网络的相似维值能对断裂构造的复杂程度做出较好的解释，可作为一种比较准确、有效的评价指标应用于断裂复杂程度的评价。

Abstract: According to the fractal theory, the fracture complexity of northern Anhui mining area is explained and analyzed by the similar dimension values of the fracture network. The results show that the complex tectonic area in northern Anhui is relatively concentrated and the fractal dimension value is high. The faults in the region are obviously regional. The lower limit of integral fractal dimension is more than 1 in the densely developed areas with large and small faults and fractures, and the structure is complicated. Similar dimension evaluation results are basically consistent with the actual exposure, and the evaluation results are better. Reasonable application of similar dimension value of fracture network in evaluation can better explain the complexity of fracture structure and can be used as a more accurate and effective evaluation index to evaluate the complexity of fracture.

1. 引言

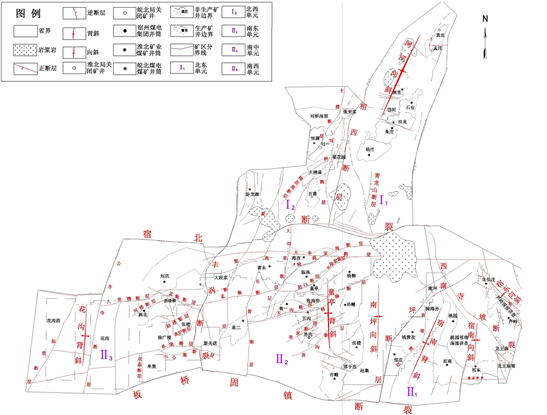
皖北矿区地质及水文地质条件复杂，断裂构造发育。整体为新生界松散层覆盖下的全隐蔽型煤田。煤田范围东起郯庐断裂，西止夏邑断层与河南永城煤田邻近，北接丰沛隆起，南止板桥–固镇断层与蚌埠隆起相接，东西长40~150 km南北宽135 km左右面积约12,350 km²。皖北矿区包括5个矿区，宿北断裂以北为闸河矿区和濉萧矿区；宿北断裂以南为宿县矿区、临涣矿区和涡阳矿区(如图1(a))。区域内断裂发育程度高，断裂网络错杂。

断裂构造的复杂程度是直接影响煤矿开采效率以及作业安全性的因素之一，井下构造裂隙作为煤层气和地下水的通道，与矿井瓦斯泄露和井下突水密切联系 [1]。所以对其定量评价对于保证煤矿安全生产以及防治和减少井下灾害事故具有重要意义。由于矿井构造的复杂性以及构造分布的极不规律，采用常规的方法难以对其进行定量评价 [2]。研究表明，断裂的破碎过程中具有随机的自相似性，断裂的分布与几何形态呈现出明显的分形结构。

(a)(b)

Figure 1. (a) The structural outline of the mining area in northern Anhui; (b) Fault trace in Wanbei mining area

图1. (a) 皖北矿区构造纲要图；(b) 皖北矿区断裂迹线

对断裂构造复杂程度进行评价，即根据其断裂网络 [3] 分布情况进行评价。而断裂网络就是一类具有明显分形结构的复杂的网络。采用常规的数学方法难以定量的描述断裂的复杂程度，分维值可以作为一类指标描述断裂网络空间分布、断层数量以及规模 [4] [5] [6]。其中分维值越大，表明断裂网络越长、断裂越发育，岩石结构越破碎，反之亦然。采用分形理论对皖北矿区的断裂构造复杂程度进行评价，有助于更充分的认识矿区的地质特性，合理选用突水防治方案和开采方式，以实现更高效、安全的生产环境。

2. 断层分维测定

2.1. 分形及相似维

分形是指各组成部分与整体之间存在的某种程度的相似的形。分形理论表述物质或者现象的局部与局部、局部与整体在结构功能和空间上的所具有的自相似性 [7] [8] [9]。分维是用来表示分形程度的一个重要的参数，根据其对维数的计算定义，可将其划分为容量维、相似维、信息维等，其中相似维(Ds)在描述断裂复杂程度中应用最为广泛 [10] [11]。

相似维( $D_s$ )：针对某一个具有自相似性的研究对象，如果其能够被划分为N个部分单元，那么每一个单元与整体之间以某个相似比呈现相似 [12]。

$D_s=-\frac{\lg N\left(r\right)}{\lg r}$ [12] (1)

2.2. 相似维求测方法

对断裂的分维值求测有多种方法，例如码尺法 [13]、康托尘集法 [14]、网格覆盖法 [15] 等，本文采用的是网格覆盖法，其能在计算机上快速拟合求解出分维值。在区域构造纲要底图上，采用可视化网格法 [16] 进行网格覆盖法测定分维。

1) 首先对需要评定的区域图做处理，在AutoCAD中打开皖北地区构造纲要图，只保留最基本的断裂迹线(图2)。

2) 将研究区划分为若干边长为r = 5000 m的正方形网格，并对各网格逐一编号并排序。

3) 分别记录含有断裂与褶皱迹线的网格数 $N\left(r\right)$，然后不断缩减网格边长，ri = r/4、ri = r/8、ri = r/16，并记录对应的网格数，按照r/2的步距进行移动，直至完成对所有网格中的数据记录。

4) 将所有的数据按照4个一组，分别对应r、r/4、r/8、r/16，进行回归分析，得到的回归曲线，取其线性回归斜率的最优值，作为断裂的分维值。

Figure 2. Schematic diagram of grid division

图2. 网格划分示意图

3. 评价结果

3.1. 回归分析评价

在excel中代入数据，进行双对数线性拟合。如图3，通过回归分析发现，各块段lgr-lgN(r)拟合关系良好，其拟合直线斜率的绝对值即为相似维值 $D_s$，其绝对值的大小反应构造的复杂程度。 $D_s$ 越大表明断裂对区域的控制作用越强，断裂切割岩层程度越大，岩层越不稳定；值越小岩石结构越完整。如表1，经统计数据查验，该区域断裂网格的相关系数大部分大于0.95以上，说明数据相关性较好、有较好的准确性。

Figure 3. Regional average r-N(r) regression curve

图3. 区域平均r-N(r)回归曲线

Table 1. Statistical results of fractal dimension of fracture (part)

表1. 断裂分维统计结果(部分)

3.2. 断裂复杂程度分析

经对分维值计算整理，该区域断裂相似维D_s在0~1.83之间，平均值1.22，相关系数大于0.7，平均相关系数0.989。褶皱相似维D_s在0~1.64之间，平均值1.27，相关系数大于0.7，平均相关系数0.97。说明该区域在所采用的划分标度下具有明显的分形特征。地区构造复杂程度是影响煤矿开采进度的重要因素，构造简单的区域，煤层往往更加稳定，安全性更高。

根据上述结果，采用《矿井地质规程》地质构造4类划分法，结合所得数据特征，分析其最大值、最小值及平均值，将其等级标准划分为简单、中等、较复杂、复杂4个等级。即D_s < 0.908、0.908 ≤D_s < 1.049、1.049 ≤D_s ≤ 1.193、D_s ≥ 1.193。参照该划分标准，选取各网格的中心点坐标以及对应的分维值，利用克里格法进行内插计算，结合区域断裂迹线，绘制区域的断裂分维(相似维)与断裂迹线分布拟合图。

Figure 4. Fitting diagram of fault fractal dimension (similarity dimension) and fault trace distribution

图4. 断裂分维(相似维)与断裂迹线分布拟合图

从图4中可以明显的看出，皖北地区构造存在明显的分区性，断裂发育较为集中，主要集中发育于矿区中、东部。大的断裂以及断裂密集发育地带分维值整体较高，构造复杂，如矿区中部区域；断裂迹线少的区域，分维值相对比较低，构造也较简单，如矿区西北部。

由于断裂发育具有不均匀性，在断裂发育较为复杂区域也存在部分相对简单区域，其迹线网络发育较为稀疏，分维值小于0.9。例如在矿区东南部分区域的断裂构造就相对简单，但周围区域的断裂迹线较多，构造较复杂，大多处于大小断层裂隙发育的密集带，维数值较高。

筛取有效网格，即在进行网格覆盖过程中包含断裂迹线的网格。对断裂分维值作统计划分，可见断裂区域整体分维值较高，大多数大于1.049，断裂构造程度属于较复杂以上。如图5，分维值大于1.193单元占比66%，分维值介于1.049~1.193占比18%，分维值介于0.908~1.049占比6%，分维值小于0.908占比10%。

根据数据以及断裂分维(相似维)与断裂迹线分布拟合图可以看出，断层网络的相似维数具有很好的规律性，利用分形维数的解释能够在结果上与矿区的实际生产揭露的情况相吻合，分析可靠。由此表明，断层网络的相似维数能够较好的表示一个矿区断裂的构造复杂程度，在定量评价中可作为一类指标对构造复杂程度加以评价分析。

Figure 5. Evaluation of complexity ratio of fault network

图5. 断裂网络复杂程度占比评价

4. 结语

分形所表示的是断层的一种非线性规律，综合反映了断层的多种特征。通过皖北矿区断裂网络的相似维值对其断裂复杂程度进行分析，结果显示，区域内的断裂构造呈现出较为明显的区域性，皖北矿区构造复杂区域分布较为集中，分维值较高。在大小断层、断裂带集中发育的稠密区域其整体分维值下限大于1，构造复杂。当分维值越大，断裂网络发育越密集、长度越长、细小断层越多，区域岩层结构越破碎；分维值较小时，断裂痕迹也就较少，岩层更完整稳定。

在地学研究中使用分形理论能对不易分析的数据做量化的处理，使断裂构造研究朝着定量化发展。在评价中合理应用断裂网络的相似维值能对断裂构造的复杂程度做出较好的解释，可作为一种比较准确、有效的评价指标应用于断裂复杂程度的评价。因此，根据相似维值对矿区断裂构造复杂程度的定量评价，有助于更充分的认识矿区的地质特性，对岩层结构类型分类处理，合理选用突水防治方案和开采方式，指导矿井生产。