基于箱形图数据清洗的水电站特性曲线修正方法

Characteristic Curve Correction Method of Hydropower Plant Based on Box-Plot Data Cleaning

摘要: 水电站和机组长期运行后，下泄流量~尾水位、水头~耗水率等特性曲线相较于设计参数存在偏差，影响水电计划编制的准确性，该问题在西南地区巨型梯级水电站群普遍存在，需要研究行之有效的解决方法。基于南方电网水电调度生产实践，提出基于箱形图数据清洗的水电站特性曲线修正方法。利用水电站海量历史运行数据构造大数据样本，通过箱型图模型去除异常数据，采用多项式拟合技术对设计曲线进行修正，能够更好地反映发电特性曲线真实关系。实际应用算例证明了方法的有效性。

Abstract: The characteristic curves, such as tailwater level and net head curve, deviate from the design parameters during the long-term operation of hydropower units, which is difficult to make an accurate hydropower scheduling plan. It is necessary to find an effective solution to address the problem, especially for the giant cascade hydropower stations in Southwest China. A correction method of characteristic curve of hydropower unit based on the box-plot data cleaning is proposed and applied in the hydropower dispatching in China Southern Power Grid. We utilized the massive historical operation data of hydropower station to construct large data samples, used the box-plot model to remove the abnormal data, and adopted the polynomial fitting technology to modify the characteristic curve. The results show that this method can better describe the power generation characteristic curve, and its effectiveness is proved by practical application examples.

1. 引言

西电东送二十多年以来，我国产生了世界最大规模梯级水电站群，集中了全球70%左右的70万kW及以上机组，世界装机容量排名前10的水电站有4座在中国。巨型单站和机组长期运行后，受巨大出库流量对下游河道冲刷以及机组磨损等因素影响，水电站下泄流量~尾水位、水头~耗水率等发电特性曲线 [1] 相较于设计参数发生了一定程度变化，有些甚至存在较大偏差，影响水电调度计划编制的准确性。该问题在水电调度运行中普遍存在，成为电网和发电企业致力于解决的基础性问题。

水电站投产后，水位、发电流量、出库流量、发电量等数据不断积累，在大数据技术 [2] [3] [4] 的引领下，为寻找水电站真实发电特性曲线提供了解决途径。然而，水电站运行数据采集依赖于各种电子传感设备，受环境以及设备稳定性影响，观测数据存在一定误差，甚至存在异常数据。如何去伪存真，消除异常数据影响，是需要研究解决的技术问题。

本文结合南方电网水电调度生产实际，提出了基于箱形图数据清洗的水电站特性曲线修正方法。利用水电站海量历史运行数据构造大数据样本，通过箱型图模型去除异常数据，采用多项式拟合技术对设计曲线进行修正，能够有效提高发电计划制作准确性，可为水电站精细化调度运行提供可靠数据支撑。

2. 原理与方法

2.1. 概念及定义

下泄流量是指水库的出库流量(包括发电流量、泄水流量)；尾水位是指水电站尾水管出口处的水位。理论上，尾水位与下泄流量关系是单调递增曲线，即出库流量越大，尾水位抬升越高。

水头是指单位重量的水具有的能量，主要取决于水库坝上水位与尾水位二者之差；耗水率是水能与电能的转换系数，含义为水电站发1千瓦时电量消耗的水量。一般情况下，出力一定时，水头与耗水率关系是单调递减曲线，即发电水头越高，耗水率越小。

2.2. 数据样本构造

坝上水位、尾水位是时刻值，下泄流量、耗水率是时段统计值，二者时间维度不同。采用算数平均法将水位转换成时段统计值，构造相应的数据样本。下泄流量、尾水位数据样本点采用式(1)构造，水头、耗水率数据样本点采用式(2)构造。

$\left(q_{out,t},\left(z_{down,t-1}+z_{down,t}\right)/2\right)$ (1)

式中： $q_{out,t}$ 为水电站在t时段的下泄流量(m³/s)， $z_{down,t-1}$ 、 $z_{down,t}$ 分别为t时段初和时段末的尾水位(m)。

$\left(\left(h_{t-1}+h_t\right)/2,r_t\right)$ (2)

式中： $h_{t-1}$ 、 $h_t$ 分别为水电站在t时段初和时段末的发电水头(m)， $r_t$ 为t时段的耗水率(m³/kWh)，且有

$h_{t-1}=z_{up,t-1}-z_{down,t-1}$ (3)

$h_t=z_{up,t}-z_{down,t}$ (4)

$r_t=q_{power,t}\times \Delta t/e_t$ (5)

式中： $z_{up,t-1}$ 、 $z_{up,t}$ 分别为水电站在t时段初和时段末的坝上水位(m)， $q_{power,t}$ 为t时段发电流量(m³/s)， $\Delta t$ 为t时段对应的时间(s)， $e_t$ 为t时段的发电量(kWh)。

为确保样本数据质量，水位、流量等数据应用前需剔除异常值。箱形图 [5] [6] [7] 是检验样本数据异常值的经典方法，一般由中位数、上四分位数、下四分位数、上限、下限五要素构成，如图1所示。

Figure 1. The sketch map of boxplot

图1. 箱形图示意图

根据箱形图理论，样本中介于下限与上限之间的数据为正常值，大于上限和小于下限的数据为异常值。上限和下限的计算表达式如下：

$U=Q_1+1.5\times IQR$ (6)

$L=Q_3-1.5\times IQR$ (7)

$IQR=Q_1-Q_3$ (8)

式中：U为上限、L为下限、 $Q_1$ 为上四分位数、 $Q_3$ 为下四分位数、 $IQR$ 为四分位差。 $Q_1$ 、 $Q_3$ 采用如下方法计算。

假设样本由k个数据组成，将其按由大到小排序后，记为数组A[n] ( $n=0,2,3,\cdots ,k-1$ )。定义变量b为 $Q_1$ 、 $Q_3$ 在数组A中的序位，变量c、d分别为序位b的整数部分和小数部分。当求解 $Q_1$ 时，令 $b=\left(k+1\right)\times 0.25$ ；当求解 $Q_3$ 时，令 $b=\left(k+1\right)\times 0.75$。则 $Q_1$ 、 $Q_3$ 计算式为：

$\text{A}\left[c-1\right]+\left(\text{A}\left[c\right]-\text{A}\left[c-1\right]\right)\times d$ (9)

为满足本文应用，在箱型图理论基础上提出分段迭代箱形图法剔除样本中异常数据，主要操作步骤为：1) 以下泄流量、尾水位为主键将原始数据样本按降序排序；2) 按一定步长范围将样本分为若干段(生成若干个数组)，每段采用箱形图法识别尾水位、耗水率异常数据；3) 从原始样本中删除异常数据，重新生成新的数据样本；4)增大下泄流量、尾水位步长，不断扩大分段样本包含的数据个数，迭代执行分段箱形图法，直到所有样本段数减少至1段。

2.3. 多项式拟合原理

最小二乘法是一种数学优化技术，通过寻找拟合数据的最佳函数匹配，使得拟合数据与实际样本数据之间误差的平方和最小，在电力系统相关专业领域有广泛的应用 [8] [9] [10] [11] [12]。最小二乘法多项式拟合数学原理如下：

假如给定m个实际样本数据点( $x_i,y_i$ ) ( $i=0,1,\cdots ,m-1$ )，求解式(10)构成的多项式函数 $p_n\left(x\right)$，使得函数拟合数据与实际样本数据的误差平方和最小，如式(11)所示。

$p_n\left(x\right)={\displaystyle \underset{k=0}{\overset{n}{\sum }}{a}_k{x}^k}$ (10)

$I={\displaystyle \underset{i=0}{\overset{m}{\sum }}{\left[p_n\left(x_i\right)-y_i\right]}^2}={\displaystyle \underset{i=0}{\overset{m}{\sum }}{\left({\displaystyle \underset{k=0}{\overset{n}{\sum }}{a}_k{x}_i^k-y_i}\right)}^2}=\min$ (11)

当拟合函数为多项式时，称为多项式拟合，满足式(10)的 $p_n\left(x\right)$ 称为最小二乘拟合多项式。根据多元函数求解极值的必要条件，对式(11)求导，可得关于 $a_0,a_1,\cdots ,a_n$ 的线性方程组，如式(12)所示。

$\left[\begin{array}{cccc}m+1& {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i}& \cdots & {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^n}\\ {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i}& {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^2}& \cdots & {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^{n+1}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^n}& {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^{n+1}}& \cdots & {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^{2n}}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_n\end{array}\right]=\left[\begin{array}{c}{\displaystyle \underset{i=0}{\overset{m}{\sum }}{y}_i}\\ {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i{y}_i}\\ ⋮\\ {\displaystyle \underset{i=0}{\overset{m}{\sum }}{x}_i^n{y}_i}\end{array}\right]$ (12)

式(12)称为正规方程组，可采用雅克比(Jacobi)迭代法 [13]、逐次超松弛法(SOR) [14] 等数值方法编程求解 $a_k$ ( $k=0,\text{1},\cdots ,n$ )，也可利用EXCEL、MATLAB等软件工具求解。

2.4. 曲线修正方法

采用2.2节方法生成下泄流量~尾水位、水头~耗水率数据样本后，采用2.3节方法拟合生成对应的多项式曲线。为构建统一的水电调度模型，水电站基础特性曲线通常以散点关系的形式使用。为此，采用如下步骤生成修正后的下泄流量~水位、水头~耗水率散点关系序列。

1) 分别找到样本数据中下泄流量、水头的最大值、最小值。

2) 以最小值为散点序列第一个点，以最大值为最后一个点，选取一定离散步长(根据应用需求确定)按照等差数列生成下泄流量、水头序列。

3) 将步骤2)生成的下泄流量、水头序列代入拟合多项式曲线，对应得到尾水位、耗水率，形成修正后的下泄流量~尾水位、水头~耗水率散点序列。

3. 应用实例

3.1. 工程背景

云南澜沧江流域梯级水电站群是我国十三大水电基地之一，已投产装机容量超过20,000 MW。选取具有代表性的某大型水电站实际应用案例，验证方法有效性。该电站装机容量4200 MW，为西电东送骨干电源，额定满发流量约2000 m³/s。水库死水位1166 m，正常蓄水位1240 m，具有年调节性能。由于装机大、调节性能好，在电力系统中承担着重要的补偿调节和调峰调频作用，实际运行中发电水头、出库流量变化明显，下泄流量~尾水位、水头~耗水率曲线的精度对发电调度影响较为显著。

3.2. 曲线拟合

选取电站2010~2019年共10年的历史数据（数据时间步长为日）构造下泄流量~尾水位、水头~耗水率数据样本，利用分段迭代箱形图法剔除异常数据。采用二次多项式拟合下泄流量~尾水位曲线，得到二次项、一次项系数、常数项分别为−3.447875 × 10⁻⁷、3.712504 × 10⁻³、9.911109 × 10²，如图2所示。采用三次多项式拟合水头~耗水率曲线，得到的三次项、二次项、一次项系数、常数项分别为3.743774 × 10⁻⁷、−2.114917 × 10⁻⁴、2.975729 × 10⁻²、1.503395，如图3所示。

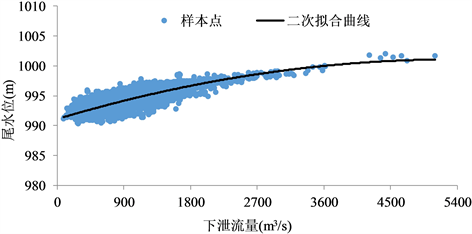
Figure 2. Discharge~tailwater level fitting curve

图2. 下泄流量~尾水位拟合曲线

Figure 3. Net head~water consumption rate fitting curve

图3. 水头~耗水率拟合曲线

3.3. 曲线修正

10年历史数据样本中，下泄流量的最大值、最小值分别为5102、50 m³/s，水头的最大值、最小值分别为248 m、160 m。分别取下泄流量、水头的离散步长为50 m³/s、1 m，生成修正后下泄流量~尾水位、水头~耗水率离散序列。图4、图5分别为设计曲线、修正曲线对比图。由图可见，修正后的曲线延长了散点序列，弥补了设计曲线数据序列长度不足，同时下泄流量、水头变化更为精细，有利于提高水库调度精度。

Figure 4. The comparison of discharge~tailwater level curve

图4. 下泄流量~尾水位曲线对比

Figure 5. The comparison of water head~water consumption rate curve

图5. 水头~耗水率曲线对比

3.4. 应用分析

采用2020年实际下泄流量、水头日数据进行检验，分别应用设计曲线和修正曲线的散点序列线性插值计算尾水位、耗水率，并和实际尾水位、耗水率数据进行对比，结果统计见表1、表2。

对尾水位偏差进行分析。由表1可知，在电站满发流量范围内，应用设计曲线计算的尾水位平均偏差达到2.8 m，采用修正曲线可将尾水位平均偏差缩小至0.24 m，精度提高了2.56 m。对耗水率偏差进行分析。由表2可知，应用设计曲线计算的耗水率平均偏差为0.067 m³/kWh；采用修正曲线可将耗水率平均误差缩小到0.007 m³/kWh，精度提高了0.06 m³/kWh。

Table 1. The water discharge obtained by different curves

表1. 尾水位计算结果对比

Table 2. The water consumption rate obtained by different curves

表2. 耗水率计算结果对比

进一步分析基础特性曲线准确性对电站调度运行的影响。采用该电站2020年逐月实际坝上水位、发电流量等数据，分别应用设计曲线和修正曲线，按照“以水定电”模型制作调度计划，计算结果对比见表3。由表可知，该电站全年实发电量163.65亿kWh，发电用水量299.7亿m³，平均耗水率1.832 m³/kWh。应用设计曲线计算的全年发电量为160.94亿kWh，与实际发电量偏差绝对值为2.7亿kWh，准确率为98.34%；应用修正曲线缩小了耗水率取值误差，计算的发电量为163.53亿kWh，电量偏差绝对值缩小到0.12亿kWh，准确率为99.92%，相比设计曲线提高了1.58%。综上分析表明，本文方法有效可行，能提高下泄流量~尾水位、水头~耗水率基础特性曲线准确性，可为水电站高效经济运行提供可靠数据支撑。

Table 3. The energy production obtained by different curves

表3. 发电量计算结果对比

4. 结论

水电站下泄流量~尾水位、水头~耗水率等特性曲线的精度影响发电计划编制的准确性，本文利用水电站实际运行海量数据构造样本，提出融合箱形图、多项式拟合的技术方法，寻找更为真实的曲线关系。该方法技术原理成熟、简单实用，相较于设计曲线可为水电调度运行提供更为准确的数据支撑，在南方电网的实际应用证明了其有效性，对解决我国水电调度类似问题具有借鉴和参考价值。

参考文献