1. 引言
目前电网企业变电站日常巡检普遍采用传统人工方式巡检,通过运行人员对变电设备进行定期的近距离看、听、闻、嗅等巡检或特殊巡检。这种巡检方式需巡检人员随身携带所需检测仪器,甚至重型仪器,劳动强度大、效率低、安全无保障,受运行人员素质、恶劣气候条件影响,巡检质量不稳定,时常产生漏判、误判 [1]。
随着现代信息技术的发展,特别是机器人技术的发展,为了解决上述问题,巡检机器人得到了广泛的应用 [2]。通过机器人上搭载的视觉观测和检测设备来对电气设备进行巡检,这样一来如何能让机器人上的设备对准要观察的设备、如何保证观测的图像清晰无重影、无边界模糊等成为巡检机器人要解决的关键问题。这对巡检机器人的结构提出了更加严格的要求,除了要有高的机械精度和结构刚度外还要有良好的动态特性。挂轨巡检机器人的升降台承载着主光学系统和探测分系统,是最为关键的部件之一,其结构直接决定着系统的性能,因此研究其动力特性对整个系统的分析设计具有重要的意义 [3]。
基于升降台的重要地位,本世纪初就已有学者着手对其性能进行分析研究。其中,国网山东电力科学研究院在国家“863计划”支持下进行了基于视觉伺服技术的升降台设计并开发出了样机进行示范应用,提出了升降台机械可靠性设计思路 [4];中科院沈阳自动化所通过热应力分析,设计研制了可在冬季下雪挂冰、夏季日晒高温条件下运行的巡检机器人升降台,开启了巡检机器人升降台的热固耦合设计 [5]。近几年,巡检机器人的研究重心开始由结构研究转向载荷搭载、系统架构、数据应用、自动控制等方面;这些研究着重解决了巡检机器人管理和应用的一系列问题,使得变电站巡检机器人系统开始进入应用阶段。但随着系统应用研究的开展,研究人员发现需进一步研究升降台的动力学特性,2018年中科院长春光学精密机械研究所高建龙根据达朗贝尔原理推导了平台的动力学方程 [6];2021年扬州大学、国网山东电力公司、广东电网公司等单位基于MATLAB和Adams平台对巡检机器人升降台进行了运动学和刚体动力学分析 [7] [8] [9]。
现有文献显示目前研究人员所作的工作主要计算升降台整体在静力学应力应变分析、运动速度加速度分析,以及空间运动范围分析,以验证设计是否满足安全和应用要求。但是,除了安全和应用要求外升降台中关键零部件特别是视轴的稳定性也是影响系统动态性能的关键因素。系统在装调阶段已保证了系统的工作性能;但在运输、工作中,在外界激扰下,特别是冲击作用下,零部件的相对位置随激扰发生改变。这种改变会导致成像模糊,影响巡检检测结果。目前还没有相关文献对这一因素进行研究分析。本文根据重庆市某变电站的挂轨巡检机器人升降台设计方案,利用有限元方法分析了在冲击载荷作用下升降台上下台面相对位置的瞬态响应特性,研究响应规律并验证结构最大响应值时是否满足使用要求。
2. 分析模型的建立
升降台结构主要包括上台面、下台面、升降支架、驱动机构、载荷设备及其他附属结构等,由于驱动机构、载荷设备及其他附属结构等比较复杂,也不是本研究关注的重点,为了使分析能顺利在ansys平台上运行,将这些结构简化成集中质量加载在各自的安装面上,模型中各个零部件之间的装配关系通过定义彼此之间的接触关系来模拟,接触单元采用CONTA174和TARGE170;整个系统实体模型用SOLID187单元划分,划分后的有限元模型如图1所示,模型共划分74154个单元。计算时根据设计要求,在上台面的安装连接处施加固定约束。
3. 模态分析
模态分析是求解结构的固有频率和对应于每一阶固有频率的振型,是动力学分析的基本内容,也是做振动响应分析的基础。
求解系统的模态就是利用相关方法求解模型特征方程的特征根及其对应的特征向量。有限元法求解模型固有频率和振型的算法很多,但以Lanczos法应用最为广泛,该方法总结了众多算法的优缺点,扬长避短,故该算法的求解精度很高,同时该算法还可以根据用户定义频率点来计算用户感兴趣的频点和振型,通用性好,故本文采用该算法进行计算。计算过程设置关注前六阶模态并扩展六阶模态。得到的前六阶模态如表1所示。

Table 1. The first six order natural frequencies of the lifting platform
表1. 升降台前六阶固有频率
表1显示升降台的前六阶模态都分布在500 Hz以内,第一阶频率为38.5 Hz,可见整个系统在设计时考虑了动态要求,系统各阶固有频率都不与变电站运行产生的频率重合。
图2是升降台前六阶变形云图,前六阶模态均为底部平台和下级叉架的变形振动,上平台和上级叉架几乎没有变形,除第1阶和第5阶模态为整个观察视轴平动变形外,其他阶模态皆会造成上下台面相对位置变化从而导致视轴偏斜变形,可见升降平台的变形对观测成像视轴稳定的影响应是系统分析的重点。


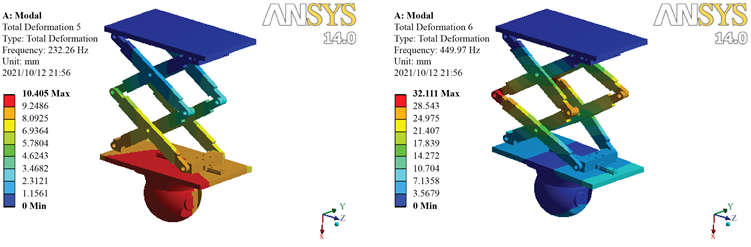
Figure 2. Deformation chart of the first six modes
图2. 前六阶模态变形图
4. 主镜筒瞬态响应分析
由模态分析可升降平台的变形对观测成像视轴稳定的影响应是系统分析的重点,受外界激扰时,会导致上下台面的位置变化,从而影响观察载荷的视轴稳定,使得成像模糊重影等,进而影响系统的巡检检测质量。因此需要重点分析上下台面相对位置在外界激扰下的响应规律。为了探寻上下台面相对位置对外界激扰的响应规律首先需定义描述上下台面相对位置的量及其计算方法。
4.1. 上下台面相对位置参数的定义及其计算方法
上下台面相对位置改变主要由三个参数来描述,分别为轴距、偏离量和相对角度漂移。其中轴距定义为上、下台面沿垂直方向的相对位移,其中以下台面位移减上台面位移计算。偏离量是用来描述上、下台面在水平面内的相对刚体位移,如图3所示,为方便表达,以圆形台面示意,假定上、下台面只有平面内的刚体移动,理想情况下上、下台面主轴重合,如图中实线所示。但由于外界激扰的影响,上、下台面位置发生变,分别位于O1和O2位置,如图中虚线轮廓所示。图中线段O1O2的长度定义为上、下台面的相对偏离量,其值由下式计算。
(1)

Figure 3. Schematic diagram for amount of deviation calculating
图3. 偏离量计算原理图
图4所示,台面M绕A、B轴的转角就定义为角度漂移。由于ansy软件中只能得到沿X,Y,Z三个坐标方向的位移,为此参考文献 [10] 可以通过选取台面上的四个节点,如图中反射镜边界与转轴的交点A1,A2和B1、B2点,通过这四个点的位移值来计算漂移角度。

Figure 4. Schematic diagram for drift angle calculating
图4. 角度漂移计算原理图
计算公式为:
(2)
式中,Di为i点处的位移量,A1A2为A1点到A2点的距离,B1B2为B1点到B2点的距离。
4.2. 瞬态响应分析激励的定义
外界激扰情况复杂多样,甚至是短时瞬态冲击激扰。这些激扰传递至升降上,使升降台的激扰也呈现任意性。系统在这类激扰的作用下没有稳定振动,只有瞬态振动,这种振动在激扰停止后按剩余振动规律振动。剩余振动持续的时间称为剩余振动时间。为了了解升降台瞬态响应特性,包括响应幅值,剩余振动时间等随载荷大小的变化规律,计算了主镜筒仅受竖直方向1 g、2 g和3 g的冲击载荷作用下上下台面相对位置变化。
4.3. 上、下台面相对位置参数响应分析
根据ansys软件计算结果,并按上文定义计算得结果如图5~图8所示。从图中可以看出,系统激扰后的剩余振动时间60 ms秒左右,95 ms时已完全稳定。各个参数的幅值在第1个周期的内的衰减率均在50%左右。

Figure 5. Axial distance curve under different loads
图5. 不同载荷下轴向间距曲线
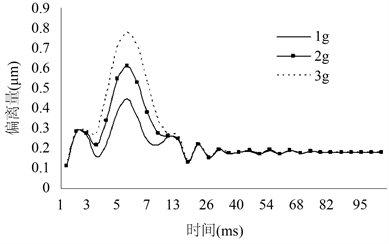
Figure 6. Deviation curve due to different loads
图6. 不同载荷下偏离量曲线

Figure 7. Response curves of drift angles of X-axis due to different loads
图7. 不同载荷下X轴角度漂移响应曲线

Figure 8. Response curves of drift angles of Y-axis due to different loads
图8. 不同载荷下Y轴角度漂移响应曲线
计算结果表明轴距、偏离量以及偏移角度的响应幅值随激扰载荷的增加在前两个响应周期内显著增加,其中首个周期响应幅值随载荷的增加明显大于第二个周期。在第二个周期以后,不同激扰载荷的响应幅值无明显的区别,剩余振动的时间亦无明显改变。由此可见、激扰载荷的改变只在前两个周期内对升降台产生较大的影响,且升降台的瞬态响应时间不随载荷的增加产生明显的改变。
计算结果表明,在激扰载荷作用下,系统振动响应时间在60 ms左右,在激扰载荷施加的瞬间升降台位置响应量达到最大值;但可以看到轴距变化始终小于5 μm,偏离量始终小于2 μm,角度漂移量始终小于50 μrad;而且经过一个周期(10ms)时间,所有参量都迅速衰减,衰减率大于50%。因此冲击响应不会对系统造成显著影响。
5. 结束语
本文运用有限元分析方法对变电站挂轨巡检机器人升降台进行动态特性分析,得出了升降台前六阶模态,结果表明升降台总体设计考虑了变电站正常运行时的振动干扰情况,各阶固有频率都避开了电站运行产生的频率。但分析发现升降台的振动主要以会引起视轴偏斜的上下台面相对位置变化为主,前六阶模态中有四阶模态皆是该种情况,从而确定分析的重点为升降平台的变形对观测成像视轴稳定的影响。为描述上下台面相对位置变化,文中定义了轴距、偏离量和角度漂移三个参量及其计算方法,利用有限元分析方法计算了它们在不同冲击载荷作用下的响应规律。分析结果表明冲击载荷的增加只会在一两个响应周期内对结构响应幅值造成影响,对响应时间没有明显影响。计算结果也表明1~3 g的冲击作用对系统没有显著影响。